Cerutti-AT2013-Graphical Subjective Logic

An Empirical Evaluation of
Geometric Subjective Logic
Operators
Federico Cerutti, Alice Toniolo, Nir Oren, Timothy J. Norman
AT-2013
Friday 2nd
August, 2013
c 2013 Federico Cerutti <f.cerutti@abdn.ac.uk>

Summary
Basic concepts of Subjective Logic and its usage in Trust Systems
Proposal of two new operators for Subjective Logic
Description of the designed experiment
Results of the empirical evaluation
c 2013 Federico Cerutti <f.cerutti@abdn.ac.uk> 2 of 19

Trustworthiness and Reputation
Trust, trustworthiness, and reputation have diﬀerent meanings in
diﬀerent approaches [Castelfranchi and Falcone, 2010]
Trustworthiness: property of an agent representing its willingness
to share information in a trustworthy manner
Reputation: property of an agent representing the subjective view
of its trustworthiness obtained from an agent with which we can
directly communicate
Subjective Logic as the way for expressing both the degree of
trustworthiness and the degree of reputation

Introduction to Subjective Logic
A subjective logic opinion is a triple ωX = bX, dX, uX
bX: belief that X holds;
dX: disbelief that X holds;
uX: uncertainty that X holds;
bX, dX, uX ∈ [0, 1] and bX + dX + uX = 1.

Opinions and Beta Distribution
Beta(p|α, β) =
Γ(α + β)
Γ(α) Γ(β)
pα−1
ββ−1
α = r + 1
β = s + 1
r: number of observations
for x
s: number of observations
for ¬x
Derived subjective logic
opinion:


b = r
r+s+2
d = s
r+s+2
u = 2
r+s+2
p

Subjective Logic Opinions and Trust Modelling:
Bootstrap
Alice has a history of interactions with Bob
Alice counts the positive (r) and negative (s) interactions with
Bob
Alice derives the trustworthiness degree of Bob as
OBob
Alice



b = r
r+s+2
d = s
r+s+2
u = 2
r+s+2
Similarly with John (OJohn
Alice)
Similarly the other agents
Bob derives OAlice
Bob and OBill
Bob
John derives OAlice
John and OBill
John
Bill derives OJohn
Bill and OBob
Bill
Alice
Bob
John
BillBob
John
Alice Bill
John
Bob
BillAlice

Transitivity
Alice wants to know what is the reputation degree for Bill
Alice asks Bob and John what is the reputation degree of Bill
(their opinion on his trustworthiness)
Either Bob or John can:
answer that he does not know Bill
respectively return OBill
Bob or OBill
John,
each of which can be
either the actual opinion
they have on Bill, or
something diﬀerent
That’s why Alice should
discount what she receives
given the trustworthiness
degree of Bob and John she derived:
OBill
Alice = (OBob
Alice ⊗ OBill
Bob ) ⊕ (OJohn
Alice ⊗ OBill
John).
Alice
Bob
John
Bill

Transitivity operators
Deﬁnition (Former Def. 5 of [Jøsang et al., 2006])
Let A, B be two agents where A’s opinion about B’s recommendations is
expressed as ωA
B = bA
B, dA
B, uA
B, aA
B and let x be a proposition where B’s
opinion about x (e.g. the degree of trustworthiness of a third agent [ed.]) is
recommended to A with the opinion ωB
X = bB
x , dB
x , uB
x , aB
x . Let
ωA:B
x = bA:B
x , dA:B
x , uA:B
x , aA:B
x be the opinion such that:



bA:B
x = bA
B bB
x
dA:B
x = bA
B dB
x
uA:B
x = dA
B + uA
B + bA
B uB
x
aA:B
x = aB
x
then ωA:B
x is called the uncertainty favouring discounted opinion of A. By
using the symbol ⊗ to designate this operation, we get ωA:B
x = ωA
B ⊗ ωB
x .

Transitivity operators
Deﬁnition (Former Thm. 1 of [Jøsang et al., 2006])
Let ωA
x = bA
x , dA
x , uA
x , aA
x and ωB
x = bB
x , dB
x , uB
x , aB
x be trust in x from A
and B respectively. The opinion ωA B
x = bA B
x , dA B
x , uA B
x , aA B
x is then
called the consensus between ωA
x and ωB
x , denoting the trust that an
imaginary agent [A, B] would have in x, as if that agent represented both A
and B. In case of Bayesian (totally certain) opinions, their relative weight
can be deﬁned as γA/B
= lim (uB
x /uA
x ).
Case I: uA
x + uB
x − uA
x uB
x = 0


bA B
x =
bA
x uB
x +bB
x uA
x
uA
x +uB
x −uA
x uB
x
dA B
x =
dA
x uB
x +dB
x uA
x
uA
x +uB
x −uA
x uB
x
uA B
x =
uA
x uB
x
uA
x +uB
x −uA
x uB
x
aA B
x =
aA
x uB
x +aB
x uA
x −(aA
x +aB
x ) uA
x uB
x
uA
x +uB
x −2 uA
x uB
x
Case II: uA
x + uB
x − uA
x uB
x = 0


bA B
x =
(γA/B
bA
x +bB
x )
(γA/B+1)
dA B
x =
(γA/B
dA
x +dB
x )
(γA/B+1)
uA B
x = 0
aA B
x =
(γA/B
aA
x +aB
x )
(γA/B+1)
By using the symbol ‘⊕’ to designate this operator, we can write
ωA B
x = ωA
x ⊕ ωB
x .

An Alternative Perspective
xO
dO + uO cos(π
3 )
sin(π
3 )
yO uO

A Graphical Discount Operator
Admissible space of opinions
Alice
Bob
John
Bill

Given a reputation opinion. . .
Alice
Bob
John
Bill

. . . we project it into the admissible space of opinions s.t.
τ ∝ α and |
# »
OBob
AliceOBill
Bob | ∝ |
# »
BOBill
Bob |
Alice
Bob
John
Bill

Finally the discounted opinion is the sum of the two vectors
Alice
Bob
John
Bill

A Graphical Fusion Operator of Discounted
Opinions
Requirements:
the fusion of an opinion Wi = Ti ◦ Ci must be balanced using
Ki = f(Ti) for some function f(·): e.g. if Alice trusts Bob more
than John, then it seems reasonable that the received opinions
are evaluated diﬀerently;
if ∀i, j Ki = Kj, then the graphical fusion operator on
W1, W2, . . . , Wn, F(W1, W2, . . . , Wn) is the centroid of the
polygon determined by n opinions;
if ∃i Ki = 0, then
F(W1, . . . , Wn) = F(W1, . . . , Wi−1, Wi+1, . . . , Wn).
Alice
Bob
John
Bill

A Graphical Fusion Operator of Discounted
Opinions
Formally:
bF(W1,...,Wn) =
1
n
i=1 Ki
n
i=1
Ki bWi
dF(W1,...,Wn) =
1
n
i=1 Ki
n
i=1
Ki dWi
uF(W1,...,Wn) =
1
n
i=1 Ki
n
i=1
Ki uWi
We considered only the case Ki = bTi +
uTi
2 .
Alice
Bob
John
Bill

Empirical Evaluation: Trust System Construction
Set of 50 agents A = {ag1, . . . , ag50}
Each agent agx is characterised by the probability of responding
truthfully to another agent’s query, namely PT
agx
∈ [0 . . . 1]
(randomly selected)
Each agent knows Ω =
For each agent agx, we determine if it can communicate with
agy = agx according to PL: if agy is connected to agx, then we
say that agy is a connection of agx (agy ∈ Nagx ).

Empirical Evaluation: Bootstrapping
Following [Ismail and Jøsang, 2002] a Beta distribution is used
for analysing repetitive experiments and deriving a subjective
logic opinion
Each agent agx asks each agent agy ∈ Nagx about Ω #B times
Given the number of exchanges when agent agy answered
truthfully (# ) and when it lied (#⊥)
O
agy
agx =
#
#B + 2
,
#⊥
#B + 2
,
2
#B + 2
Opinion derived by the (omniscient) experimenter
O
agy
Exp = PT
agy
, (1 − PT
agy
), 0

Empirical Evaluation: Network Exploration
An “explorer” agS ∈ A is randomly selected
agS asks each agent in its connections about the trustworthiness
it has of its connections (e.g. Alice asks both Bob and John
(separately) about which agents they know and what is their
opinion of them)
For each agent agz they claim to know (e.g. Bill), agS computes
Oagz
agS |J = (O
agy1
agS ⊗ Oagz
agy1
) ⊕ . . . ⊕ (O
agyn
agS ⊗ Oagz
agyn
) (Jøsang
operators), and Oagz
agS |G = F((O
agy1
agS ◦ Oagz
agy1
), . . . , (O
agyn
agS ◦ Oagz
agyn
)
(the graphical operators)
Now agz is known and can be directly questioned about other
agents it might now
The explorations ends when no new agents are discovered

Empirical Evaluation: Results
For each run, for each value of PL, 250 explorations over 10
diﬀerent networks were carried out (overall 12500 explorations
across 500 diﬀerent networks)
For small values of PL, the graphical operators return opinions
closer to the “ideal” one than Jøsang’s by a factor 2 (on the
average dJ
dG
2), or, in other terms, approx. 50% closer;
The greater the PL, the more similar the performance of the two
sets of operators, the smaller the standard deviation on the
results obtained by the experiments;
The overall average on the logarithmic scale is 1.56 (36% on the
linear scale).

Empirical Evaluation: Results
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0 5 10 15 20 25 30
Averageofthescalarlogaritmiccomparisonvalue
PL
Average Logaritmic Comparison with respect to the Probability of Initial Connection PL
Run01
Run02
Run03
Run04
Run05
Run06
Run07
Run08
Run09
Run10

Conclusions
Empirical investigation on discount and fusion operators for
Subjective Logic
Proposal of two new operators for Subjective Logic based on
graphical properties
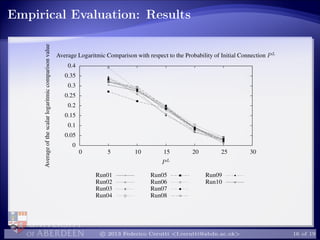
Empirical comparison of the new proposal w.r.t. Jøsang
operators, with improving of the results of 36% (on the average)
What’s next:
Study of random graph generation (e.g. scale-free networks. . . )
Experimental evaluation in presence of more uncertainty (lowering
the number of interactions in the bootstrap phase)
Reaching a common methodology with [Kaplan et al., 2013]

Acknowledgement
Research was sponsored by US Army Research laboratory
and the UK Ministry of Defence and was accomplished under
Agreement Number W911NF-06-3-0001. The views and
conclusions contained in this document are those of the
authors and should not be interpreted as representing the
oﬃcial policies, either expressed or implied, of the US Army
Research Laboratory, the U.S. Government, the UK Ministry
of Defense, or the UK Government. The US and UK
Governments are authorized to reproduce and distribute
reprints for Government purposes notwithstanding any
copyright notation hereon.

References I
[Castelfranchi and Falcone, 2010] Castelfranchi, C. and Falcone, R. (2010).
Trust theory: A socio-cognitive and computational model.
Wiley Series in Agent Technology.
[Ismail and Jøsang, 2002] Ismail, R. and Jøsang, A. (2002).
The beta reputation system.
In Prooceedings of BLED 2002.
[Jøsang et al., 2006] Jøsang, A., Pope, S., and Marsh, S. (2006).
Exploring diﬀerent types of trust propagation.
In Proceedings of the 4th International Conference on Trust Management (iTrust’06).
[Kaplan et al., 2013] Kaplan, L. M., Sensoy, M., Tang, Y., Chakraborty, S., Bisdikian, C., and de Mel,
G. (2013).
Reasoning under uncertainty: Variations of subjective logic deduction.
In Proceedings of the Sixteenth International Conference on Information Fusion.

Cerutti-AT2013-Graphical Subjective Logic

More Related Content

Viewers also liked

Similar to Cerutti-AT2013-Graphical Subjective Logic

More from Federico Cerutti

Recently uploaded

Cerutti-AT2013-Graphical Subjective Logic