The document discusses the evolution of argumentation in artificial intelligence, reflecting on twenty years since Dung's foundational framework. It explores various argumentation schemes, semantics, and algorithms, addressing the theoretical and practical aspects of argumentative reasoning. Additionally, it touches on applications in multi-agent systems and the complexity of different argumentation semantics.









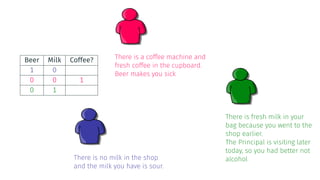
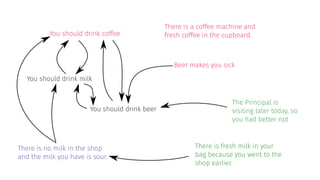

![[Dun95]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-20-320.jpg)


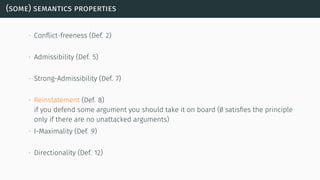
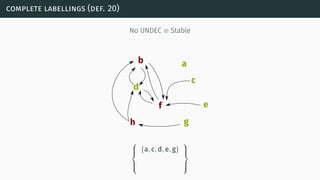
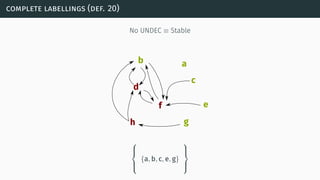
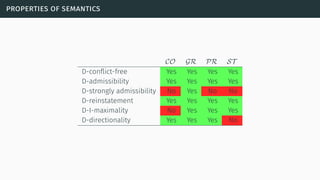
![(some) semantics properties
[BG07] [BCG11]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-23-320.jpg)





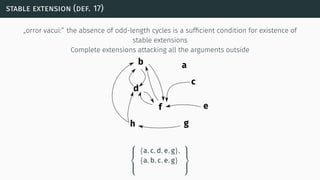
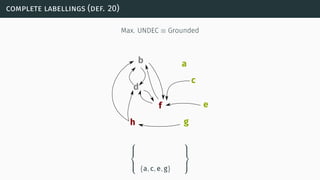
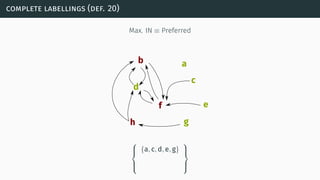
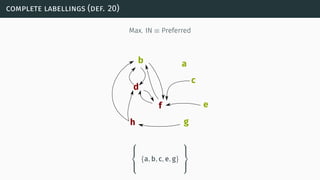
![complexity
[DW09]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-42-320.jpg)

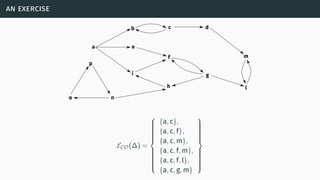
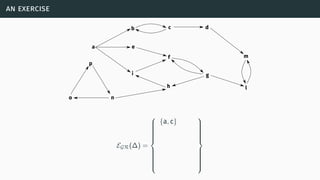
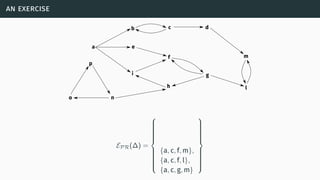
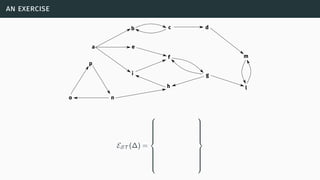
![skepticisms and comparisons of sets of extensions
[BG09b]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-50-320.jpg)

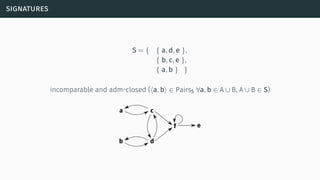
![signatures
[Dun+14]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-52-320.jpg)







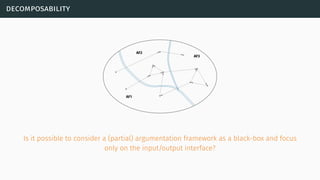
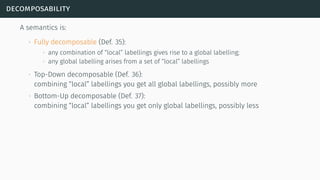
![decomposability
[Bar+14]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-61-320.jpg)




![[WRM08]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-70-320.jpg)



![[Rah+11]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-76-320.jpg)
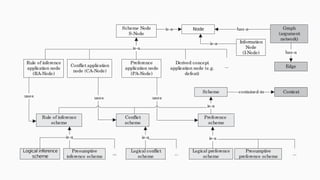
![[Bex+13]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-79-320.jpg)



![value based argumentation framework
[BA09]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-84-320.jpg)

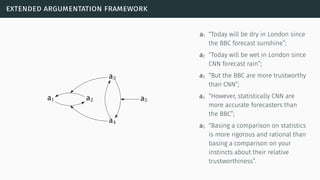
![extended argumentation framework
[Mod09]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-87-320.jpg)
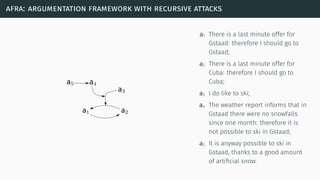
![afra: argumentation framework with recursive attacks
[Bar+11]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-90-320.jpg)
![bipolar argumentation framework
[CL05]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-93-320.jpg)



![delp: defeasible logic programming
[SL92] [GS14]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-97-320.jpg)
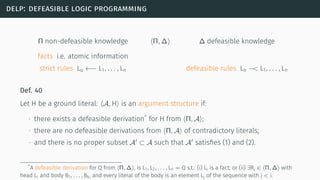




![assumption based argumentation framework
[Bon+97] [Ton14]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-103-320.jpg)




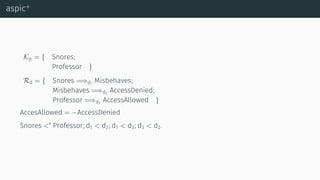
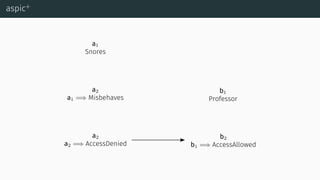
![aspic+
[Pra10] [MP13] [MP14]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-108-320.jpg)





![deductive argumentation
[BH01] [GH11] [BH14]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-117-320.jpg)

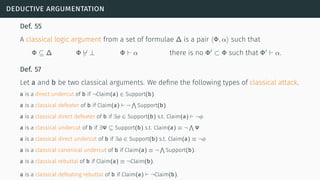


![a logic for clinical knowledge
[HW12] [Wil+15]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-122-320.jpg)

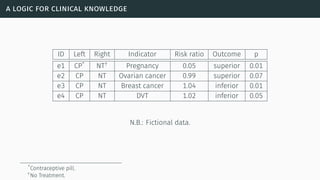
![a logic for clinical knowledge
Def. 60
For any pair of arguments ai and aj, and a preference relation R, ai attacks aj with respect
to R iff ai conflicts with aj and it is not the case that aj is strictly preferred to ai according
to R.
A domain-specific benefit preference relation is defined in [HW12]
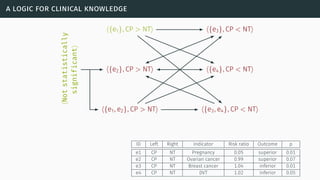
Def. 61 (Meta arguments)
For a ∈ Arg(evidence), if there is an e ∈ support(a) such that:
∙ e is not statistically significant, and e is not a side-effect, then this is an attacker:
⟨Not statistically significant⟩;
∙ e is a non-randomised and non-blind trial, then this is an attacker:
⟨Non-randomized & non-blind trials⟩;
∙ e is a meta-analysis that concerns a narrow patient group, then this is an attacker:
⟨Meta-analysis for a narrow patient group⟩.](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-124-320.jpg)

![epistemic approach
[Thi12] [Hun13]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-128-320.jpg)
![epistemic approach
[HT14] [BGV14]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-129-320.jpg)
![epistemic approach
An epistemic probability distribution*
for an argumentation framework ∆ = ⟨A, → ⟩ is:
P : A → [0, 1]
Def. 65
For an argumentation framework AF = ⟨A, →⟩ and a probability assignment P, the
epistemic extension is
{a ∈ A | P(a) > 0.5}
*In the tutorial a way to compute it for arguments based on classical deduction.](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-130-320.jpg)


![structural approach
[Hun14]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-133-320.jpg)
![structural approach
P : {∆′
⊑ ∆} → [0, 1]
Subframework Probability
∆1 a ↔ b 0.09
∆2 a 0.81
∆3 b 0.01
∆4 0.09
PGR({a, b}) = = 0.00
PGR({a}) = P(∆2) = 0.81
PGR({b}) = P(∆3) = 0.01
PGR({}) = P(∆1) + P(∆4) = 0.18](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-134-320.jpg)
![a computational framework
[Li15]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-135-320.jpg)
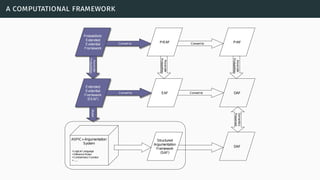

![[Ton+15]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-138-320.jpg)

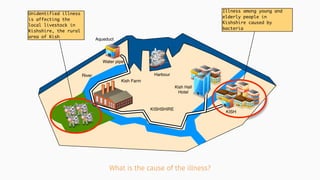
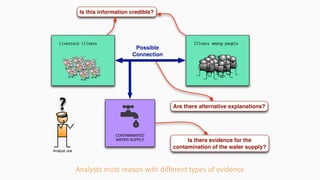

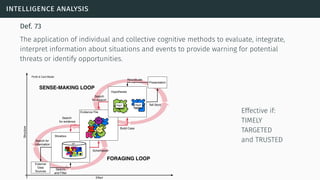
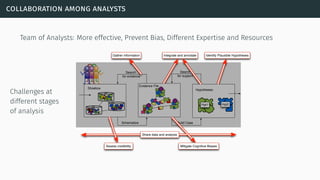
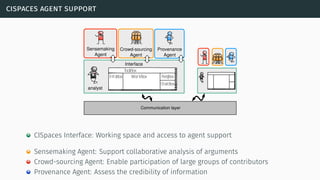




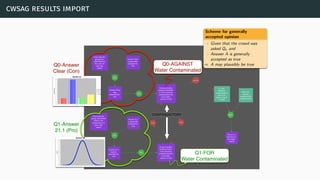
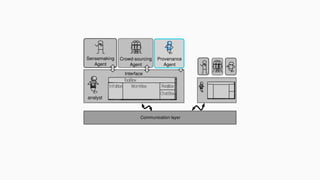
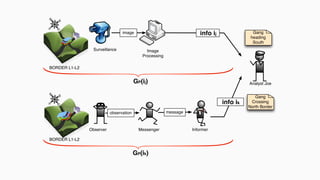


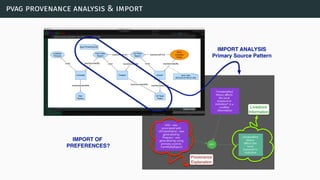
![theories/technologies integrated
∙ Argument representation:
∙ Argument Schemes and Critical questions (domain specific)
∙ „Bipolar-like” graph for user consumption
∙ AIF (extension for provenance)
∙ ASPIC(+)
∙ Arguments based on preferences (partially under development)
∙ Theoretical framework for acceptability status:
∙ AF
∙ PrAF (case study for [Li15])
∙ AFRA for preference handling (under development)
∙ Computational machinery: jArgSemSAT](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-159-320.jpg)

![[Cha+15]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-161-320.jpg)
![ad-hoc procedures
ArgTools
[NAD14]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-162-320.jpg)

![csp-based approach
ConArg
[BS12]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-164-320.jpg)


![asp-based approach
ASPARTIX-D / ASPARTIX-V / DIAMOND
[EGW10] [Dvo+11]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-167-320.jpg)

![sat-based approaches
Cegartix
[Dvo+12]
ArgSemSAT/jArgSemSAT/LabSATSolver
[Cer+14b]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-169-320.jpg)
![sat-based approaches
[Dvo+12]
∧
a→b
(¬xa ∨ ¬xb)∧
∧
b→c
¬xc ∨
∨
a→b
xa
](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-170-320.jpg)
![sat-based approaches
[Cer+14b]
If a1 is not attacked, Lab(a1) = in
C1
Lab(a1) = in ⇔ ∀a2 ∈ a−
1 Lab(a2) = out
Lab(a1) = out ⇔ ∃a2 ∈ a−
1 : Lab(a2) = in
Lab(a1) = undec ⇔ ∀a2 ∈ a−
1 Lab(a2) ̸= in ∧ ∃a3 ∈ a−
1 :
Lab(a3) = undec](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-171-320.jpg)
![sat-based approaches
[Cer+14b]
∧
i∈{1,...,k}
(
(Ii ∨ Oi ∨ Ui) ∧ (¬Ii ∨ ¬Oi)∧(¬Ii ∨ ¬Ui) ∧ (¬Oi ∨ ¬Ui)
)
∧
∧
{i|ϕ(i)−=∅}
(Ii ∧ ¬Oi ∧ ¬Ui) ∧
∧
{i|ϕ(i)−̸=∅}
Ii ∨
∨
{j|ϕ(j)→ϕ(i)}
(¬Oj)
∧
∧
{i|ϕ(i)−̸=∅}
∧
{j|ϕ(j)→ϕ(i)}
¬Ii ∨ Oj
∧
∧
{i|ϕ(i)−̸=∅}
∧
{j|ϕ(j)→ϕ(i)}
¬Ij ∨ Oi
∧
∧
{i|ϕ(i)−̸=∅}
¬Oi ∨
∨
{j|ϕ(j)→ϕ(i)}
Ij
∧
∧
{i|ϕ(i)−̸=∅}
∧
{k|ϕ(k)→ϕ(i)}
Ui ∨ ¬Uk ∨
∨
{j|ϕ(j)→ϕ(i)}
Ij
∧
∧
{i|ϕ(i)−̸=∅}
∧
{j|ϕ(j)→ϕ(i)}
(¬Ui ∨ ¬Ij)
∧
¬Ui ∨
∨
{j|ϕ(j)→ϕ(i)}
Uj
](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-172-320.jpg)
![sat-based approaches
[Cer+14b]
If a1 is not attacked, Lab(a1) = in
Ca
1
Lab(a1) = in ⇔ ∀a2 ∈ a−
1 Lab(a2) = out
Lab(a1) = out ⇔ ∃a2 ∈ a−
1 : Lab(a2) = in](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-173-320.jpg)
![sat-based approaches
[Cer+14b]
If a1 is not attacked, Lab(a1) = in
Cb
1
Lab(a1) = out ⇔ ∃a2 ∈ a−
1 : Lab(a2) = in
Lab(a1) = undec ⇔ ∀a2 ∈ a−
1 Lab(a2) ̸= in ∧ ∃a3 ∈ a−
1 :
Lab(a3) = undec](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-174-320.jpg)
![sat-based approaches
[Cer+14b]
If a1 is not attacked, Lab(a1) = in
Cc
1
Lab(a1) = in ⇔ ∀a2 ∈ a−
1 Lab(a2) = out
Lab(a1) = undec ⇔ ∀a2 ∈ a−
1 Lab(a2) ̸= in ∧ ∃a3 ∈ a−
1 :
Lab(a3) = undec](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-175-320.jpg)
![sat-based approaches
[Cer+14b]
If a1 is not attacked, Lab(a1) = in
C2
Lab(a1) = in ⇒ ∀a2 ∈ a−
1 Lab(a2) = out
Lab(a1) = out ⇒ ∃a2 ∈ a−
1 : Lab(a2) = in
Lab(a1) = undec ⇒ ∀a2 ∈ a−
1 Lab(a2) ̸= in ∧ ∃a3 ∈ a−
1 :
Lab(a3) = undec](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-176-320.jpg)
![sat-based approaches
[Cer+14b]
If a1 is not attacked, Lab(a1) = in
C3
Lab(a1) = in ⇐ ∀a2 ∈ a−
1 Lab(a2) = out
Lab(a1) = out ⇐ ∃a2 ∈ a−
1 : Lab(a2) = in
Lab(a1) = undec ⇐ ∀a2 ∈ a−
1 Lab(a2) ̸= in ∧ ∃a3 ∈ a−
1 :
Lab(a3) = undec](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-177-320.jpg)
![sat-based approaches
[Cer+14b]
50
60
70
80
90
100
50 100 150 200IPCnormalisedto100
Number of arguments
IPC normalised to 100 with respect to the number of arguments
C1
Ca
1
Cb
1
Cc
1
C2
C3](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-178-320.jpg)
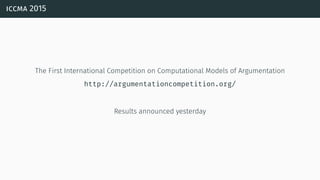
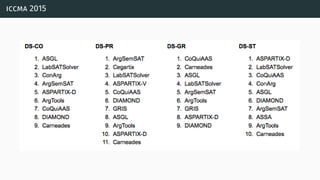

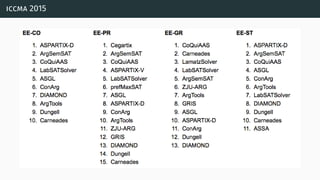
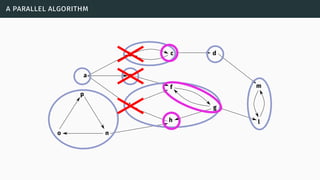
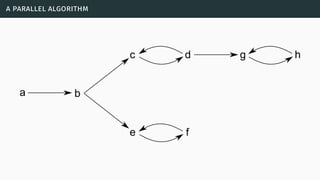
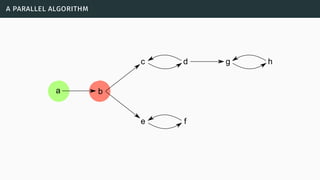
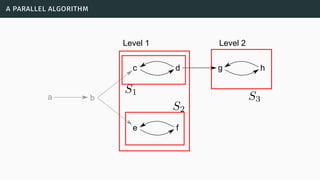
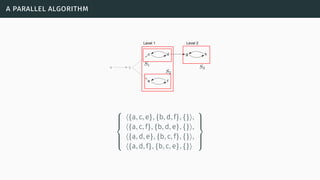
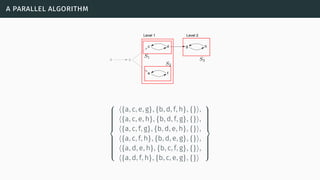
![a parallel algorithm
[BGG05] [Cer+14a] [Cer+15]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-183-320.jpg)
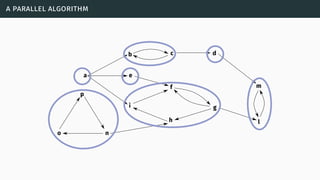

![[VCG14] [CGV14]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-193-320.jpg)








![belief revision and argumentation
[FKS09] [FGS13]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-203-320.jpg)
![belief revision and argumentation
Potential cross-fertilisation
Argumentation in Belief Revision
∙ Justification-based truth maintenance
system
∙ Assumption-based truth maintenance
system
Some conceptual differences:
in revision, external beliefs are
compared with internal beliefs and,
after a selection process, some
sentences are discarded, other
ones are accepted. [FKS09]
Belief Revision in Argumentation
∙ Changing by adding or deleting an
argument.
∙ Changing by adding or deleting a set of
arguments.
∙ Changing the attack (and/or defeat)
relation among arguments.
∙ Changing the status of beliefs (as
conclusions of arguments).
∙ Changing the type of an argument (from
strict to defeasible, or vice versa).](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-204-320.jpg)
![abstract dialectical framework
[Bre+13]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-205-320.jpg)

![argumentation and social networks
[LM11] [ET13]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-207-320.jpg)
![argumentation and social networks
a:The Wonder-Phone is the
best new generation
phone.
+20 -20
b: No, the Magic-Phone is
the best new generation
phone.
+ 20 - 20
c: here is a [link] to a review
of the Magic-Phone giving
poor scores due to bad
battery performance
+60 -10.
d: author of c is ignorant, since
subsequent reviews noted that
only one of the first editions
had such problems: [links].
+10 -40
e: d is wrong. I found out
c) knows about that but
withheld the information.
Here's a [link] to another
thread proving it!
+40 -10](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-208-320.jpg)
![argumentation and social networks
a:The Wonder-Phone is the best
new generation phone.
+20 -20 b: No, the Magic-Phone is the
best new generation phone.
+ 20 - 20
c: here is a [link] to a review
of the Magic-Phone giving
poor scores due to bad
battery performance
+60 -10.
d: author of c is ignorant, since
subsequent reviews noted that
only one of the first editions had
such problems: [links].
+10 -40
e: d is wrong. I found out c)
knows about that but
withheld the information.
Here's a [link] to another
thread proving it!
+40 -10](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-209-320.jpg)
![argumentation and social networks
a:The Wonder-Phone is the best
new generation phone.
+20 -20
b: No, the Magic-Phone is the best
new generation phone.
+ 20 - 20
c: here is a [link] to a review of the Magic-
Phone giving poor scores due to bad
battery performance
+60 -10.
d: author of c is ignorant, since subsequent
reviews noted that only one of the first editions
had such problems: [links].
+10 -40
e: d is wrong. I found out c)
knows about that but
withheld the information.
Here's a [link] to another
thread proving it!
+40 -10](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-210-320.jpg)

![argument mining
[CV12] [Bud+14]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-212-320.jpg)
![natural language interfaces
[CTO14] [Cam+14]](https://image.slidesharecdn.com/tutorial-web-150803131119-lva1-app6891/85/Argumentation-in-Artificial-Intelligence-214-320.jpg)