The document presents a SAT-based approach for computing preferred extensions in abstract argumentation, detailing the theoretical framework, algorithm, and empirical evaluation. It explores complete labellings, their encodings, and how to use SAT solvers for enumerating preferred extensions, citing performance metrics and comparisons with existing systems. The authors conclude that their method demonstrates superior performance and outline future work on broader argumentation semantics.

1. A SAT-based Approach for
Computing Extensions in
Abstract Argumentation
Federico Cerutti, Paul E. Dunne, Massimiliano Giacomin, Mauro Vallati
TAFA-2013
Sunday 4th
August, 2013
c 2013 Federico Cerutti <f.cerutti@abdn.ac.uk>

2. Summary
Background in abstract argumentation
SAT encodings of complete labellings with interesting theoretical
properties
An algorithm exploiting SAT solvers for enumerating preferred
extensions
Empirical evaluation of the algorithm

3. Background
Definition
Given an AF Γ = A, R :
a set S ⊆ A is conflict–free if a, b ∈ S s.t. a → b;
an argument a ∈ A is acceptable with respect to a set S ⊆ A if
∀b ∈ A s.t. b → a, ∃ c ∈ S s.t. c → b;
a set S ⊆ A is admissible if S is conflict–free and every element of
S is acceptable with respect to S;
a set S ⊆ A is a complete extension, i.e. S ∈ ECO(Γ), iff S is
admissible and ∀a ∈ A s.t. a is acceptable w.r.t. S, a ∈ S;
a set S ⊆ A is a preferred extension, i.e. S ∈ EPR(Γ), iff S is a
maximal (w.r.t. set inclusion) admissible set.
N.B.: EPR(Γ) ⊆ ECO(Γ)

4. Background
Definition
Let A, R be an argumentation framework. A total function
Lab : A → {in, out, undec} is a complete labelling iff it satisfies the
following conditions for any a ∈ A:
Lab(a) = in ⇔ ∀b ∈ a−Lab(b) = out;
Lab(a) = out ⇔ ∃b ∈ a− : Lab(b) = in;
Lab(a) = undec ⇔ ∀b ∈ a−Lab(b) = in ∧ ∃c ∈ a− : Lab(c) =
undec;
From [Caminada, 2006], preferred extensions are in one-to-one
correspondence with those complete labellings maximizing the set of
arguments labelled in.

5. An Approach for Expressing the Complete
Labelling as a SAT Problem
Given an AF Γ = A, R , ΠΓ is a boolean formula (complete labelling
formula) such that each satisfying assignment of the formula
corresponds to a complete labelling:
k = |A|
φ : {1, . . . , k} → A is a bijection (the inverse map is φ−1)
For each argument φ(i) we define three boolean variables:
Ii, which is true when argument φ(i) is labelled in, false otherwise;
Oi, which is true when argument φ(i) is labelled out, false
otherwise;
Ui, which is true when argument φ(i) is labelled undec, false
otherwise;
V(Γ) ∪1≤i≤|A|{Ii, Oi, Ui} (set of variables for the AF Γ)

6. SAT Encoding of Complete Labelling: C1
Lab is a total function;
If a is not attacked, Lab(a) = in;
Lab(a) = in ⇔ ∀b ∈ a−Lab(b) = out;
Lab(a) = out ⇔ ∃b ∈ a− : Lab(b) = in;
Lab(a) = undec ⇔ ∀b ∈ a−Lab(b) = in ∧ ∃c ∈ a− : Lab(c) =
undec.

7. SAT Encoding of Complete Labelling: C1
i∈{1,...,k}
(Ii ∨ Oi ∨ Ui) ∧ (¬Ii ∨ ¬Oi)∧(¬Ii ∨ ¬Ui) ∧ (¬Oi ∨ ¬Ui) ∧
{i|φ(i)−=∅}
(Ii ∧ ¬Oi ∧ ¬Ui) ∧
{i|φ(i)−=∅}

Ii ∨


{j|φ(j)→φ(i)}
(¬Oj )



 ∧
{i|φ(i)−=∅}


{j|φ(j)→φ(i)}
¬Ii ∨ Oj

 ∧
{i|φ(i)−=∅}


{j|φ(j)→φ(i)}
¬Ij ∨ Oi

 ∧
{i|φ(i)−=∅}

¬Oi ∨


{j|φ(j)→φ(i)}
Ij



 ∧
{i|φ(i)−=∅}


{k|φ(k)→φ(i)}

Ui ∨ ¬Uk ∨


{j|φ(j)→φ(i)}
Ij





 ∧
{i|φ(i)−=∅}




{j|φ(j)→φ(i)}
(¬Ui ∨ ¬Ij )

 ∧

¬Ui ∨


{j|φ(j)→φ(i)}
Uj





 ∧

8. SAT Encoding of Complete Labelling: Ca
1
Lab is a total function;
If a is not attacked, Lab(a) = in;
Lab(a) = in ⇔ ∀b ∈ a−Lab(b) = out;
Lab(a) = out ⇔ ∃b ∈ a− : Lab(b) = in;
Lab(a) = undec ⇔ ∀b ∈ a−Lab(b) = in ∧ ∃c ∈ a− : Lab(c) =
undec.

9. SAT Encoding of Complete Labelling: Ca
1
i∈{1,...,k}
(Ii ∨ Oi ∨ Ui) ∧ (¬Ii ∨ ¬Oi)∧(¬Ii ∨ ¬Ui) ∧ (¬Oi ∨ ¬Ui) ∧
{i|φ(i)−=∅}
(Ii ∧ ¬Oi ∧ ¬Ui) ∧
{i|φ(i)−=∅}

Ii ∨


{j|φ(j)→φ(i)}
(¬Oj )



 ∧
{i|φ(i)−=∅}


{j|φ(j)→φ(i)}
¬Ii ∨ Oj

 ∧
{i|φ(i)−=∅}


{j|φ(j)→φ(i)}
¬Ij ∨ Oi

 ∧
{i|φ(i)−=∅}

¬Oi ∨


{j|φ(j)→φ(i)}
Ij



 ∧
(((((((((((((((((((((((hhhhhhhhhhhhhhhhhhhhhhh
{i|φ(i)−=∅}


{k|φ(k)→φ(i)}

Ui ∨ ¬Uk ∨


{j|φ(j)→φ(i)}
Ij





 ∧
((((((((((((((((((((((((((((hhhhhhhhhhhhhhhhhhhhhhhhhhhh
{i|φ(i)−=∅}




{j|φ(j)→φ(i)}
(¬Ui ∨ ¬Ij )

 ∧

¬Ui ∨


{j|φ(j)→φ(i)}
Uj





 ∧

10. SAT Encoding of Complete Labelling: Cb
1
Lab is a total function;
If a is not attacked, Lab(a) = in;
Lab(a) = in ⇔ ∀b ∈ a−Lab(b) = out;
Lab(a) = out ⇔ ∃b ∈ a− : Lab(b) = in;
Lab(a) = undec ⇔ ∀b ∈ a−Lab(b) = in ∧ ∃c ∈ a− : Lab(c) =
undec.

11. SAT Encoding of Complete Labelling: Cc
1
Lab is a total function;
If a is not attacked, Lab(a) = in;
Lab(a) = in ⇔ ∀b ∈ a−Lab(b) = out;
Lab(a) = out ⇔ ∃b ∈ a− : Lab(b) = in;
Lab(a) = undec ⇔ ∀b ∈ a−Lab(b) = in ∧ ∃c ∈ a− : Lab(c) =
undec.

12. SAT Encoding of Complete Labelling: C2
Lab is a total function;
If a is not attacked, Lab(a) = in;
Lab(a) = in ⇒ ∀b ∈ a−Lab(b) = out;
Lab(a) = out ⇒ ∃b ∈ a− : Lab(b) = in;
Lab(a) = undec ⇒
∀b ∈ a−Lab(b) = in ∧ ∃c ∈ a− : Lab(c) = undec.

13. SAT Encoding of Complete Labelling: C3
Lab is a total function;
If a is not attacked, Lab(a) = in;
Lab(a) = in ⇐ ∀b ∈ a−Lab(b) = out;
Lab(a) = out ⇐ ∃b ∈ a− : Lab(b) = in;
Lab(a) = undec ⇐
∀b ∈ a−Lab(b) = in ∧ ∃c ∈ a− : Lab(c) = undec.

14. Equivalence of the Encodings
Proposition
The encodings C1, Ca
1 , Cb
1, Cc
1, C2, C3 are equivalent.
Let us note that Ca
1 and C2 correspond to the alternative definitions
of complete labellings in [Caminada and Gabbay, 2009], where a proof
of their equivalence is provided.

15. Exploiting SAT Solvers for Enumerating
Preferred Extensions
Algorithm 1 Enumerating the preferred extensions of an AF
1: Input: Γ = A, R
2: Output: Ep ⊆ 2A
3: Ep := ∅
4: cnf := ΠΓ
5: repeat
6: prefcand := ∅
7: cnfdf := cnf
8: repeat
9: lastcompfound := SS(cnfdf)
10: if lastcompfound ! = ε then
11: prefcand := lastcompfound
12: for a ∈ INARGS(lastcompfound) do
13: cnfdf := cnfdf ∧ Iφ−1(a)
14: end for
15: remaining := FALSE
16: for a ∈ A INARGS(lastcompfound) do
17: remaining := remaining ∨ Iφ−1(a)
18: end for
19: cnfdf := cnfdf ∧ remaining
20: end if
21: until (lastcompfound ! = ε ∧ INARGS(lastcompfound) ! = A)
22: if prefcand ! = ∅ then
23: Ep := Ep ∪ {INARGS(prefcand)}
24: oppsolution := FALSE
25: for a ∈ A INARGS(prefcand) do
26: oppsolution := oppsolution ∨ Iφ−1(a)
27: end for
28: cnf := cnf ∧ oppsolution
29: end if
30: until (prefcand ! = ∅)
31: if Ep = ∅ then
32: Ep = {∅}
33: end if
34: return Ep

16. Exploiting SAT Solvers for Enumerating
Preferred Extensions: an Example
Complete extensions:
{}, {f}, {d}, {a, f}, {b, d}, {d, f}, {b, d, e}, {a, c, f}, {b, d, f},
{a, d, f}

17. Exploiting SAT Solvers for Enumerating
Preferred Extensions: an Example
First complete extension found (not deterministic)

18. Exploiting SAT Solvers for Enumerating
Preferred Extensions: an Example
Forcing the search process for finding additional in arguments given
the found complete

19. Exploiting SAT Solvers for Enumerating
Preferred Extensions: an Example
Another complete found. . .

20. Exploiting SAT Solvers for Enumerating
Preferred Extensions: an Example
. . . which is also preferred: {a, d, f}

21. Exploiting SAT Solvers for Enumerating
Preferred Extensions: an Example
Searching for other complete extensions. . .

22. Exploiting SAT Solvers for Enumerating
Preferred Extensions: an Example
. . . for instance {b, d} . . .

23. Exploiting SAT Solvers for Enumerating
Preferred Extensions: an Example
. . . from which we compute the preferred extensions {b, d, f}.

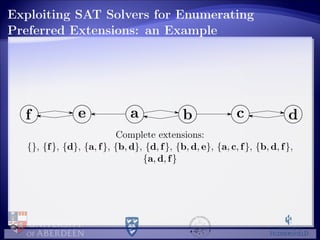
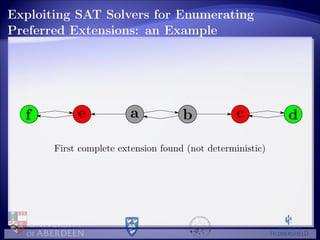
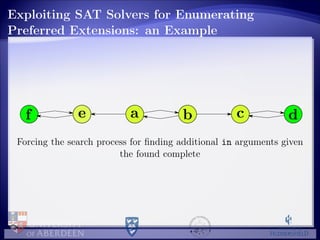
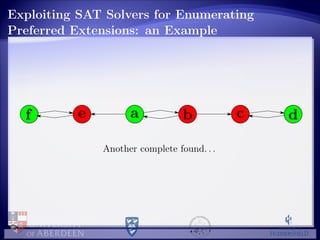
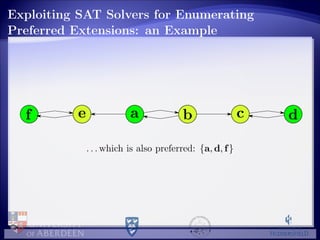
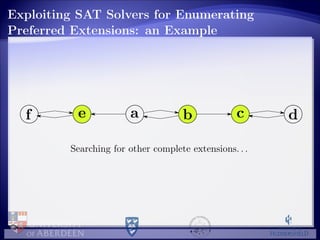
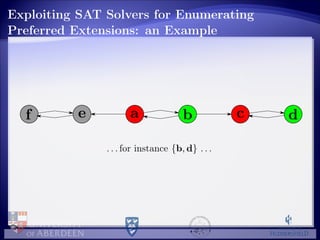
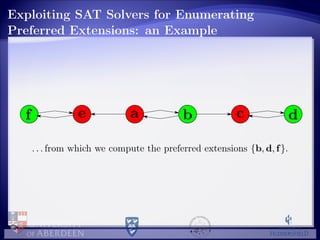
24. Empirical Evaluation: the Experiment
Two SAT solvers considered (separately):
PrecoSAT [Biere, 2009], SAT Competition 2009 winner
(Application track) → PS-PRE;
Glucose
[Audemard and Simon, 2009, Audemard and Simon, 2012] SAT
Competition 2011 and SAT Challenge 2012 winner (Application
track) → PS-GLU
Random generated 2816 AFs divided in different classes according to two
dimensions:
|A|: ranging from 25 to 200 with a step of 25;
generation of the attack relations:
fixing the probability patt that there is an attack for each ordered
pair of arguments (self-attacks are included), step of 0.25
selecting randomly the number natt of attacks in it
the extreme cases of empty attack relation (patt = natt = 0) and of
fully connected attack relation (patt = 1, natt = |A|2
)

25. Empirical Evaluation: the Analysis Using the
International Planning Competition (IPC) Score
For each test case (in our case, each test AF) let T∗ be the best
execution time among the compared systems (if no system
produces the solution within the time limit, the test case is not
considered valid and ignored).
For each valid case, each system gets a score of
1/(1 + log10(T/T∗)), where T is its execution time, or a score of 0
if it fails in that case. Runtimes below 1 sec get by default the
maximal score of 1.
The (non normalized) IPC score for a system is the sum of its
scores over all the valid test cases. The normalised IPC score
ranges from 0 to 100 and is defined as
(IPC/# of valid cases) ∗ 100.

26. Empirical Evaluation: Comparison of Different
Encodings
50
60
70
80
90
100
50 100 150 200
IPCnormalisedto100
Number of arguments
IPC normalised to 100 with respect to the number of arguments
C1
Ca
1
Cb
1
Cc
1
C2
C3

27. Empirical Evaluation: Comparison with Aspartix,
Aspartix Meta, [Nofal et al., 2012]
60
65
70
75
80
85
90
95
100
50 100 150 200
%ofsuccess
Number of arguments
Percentage of success
ASP
ASP-META
NOF
PS-PRE
PS-GLU

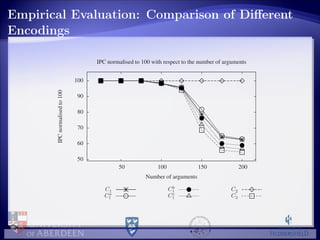
28. Empirical Evaluation: Comparison with Aspartix,
Aspartix Meta, [Nofal et al., 2012]
20
30
40
50
60
70
80
90
100
50 100 150 200
IPCnormalisedto100
Number of arguments
IPC normalised to 100 with respect to the number of arguments
ASP
ASP-META
NOF
PS-PRE
PS-GLU

29. Conclusions
Novel SAT-based approach for preferred extension enumeration in
abstract argumentation
Assessed its performances by an empirical comparison with
well-known state-of-the-art systems
Evidence that different encodings, although theoretically
equivalent, lead to very different empirical results
The proposed approach outperforms the state-of-the-art
Future works (currently ongoing):
Implementation of the other Labelling-based semantics
(Grounded, Complete, Stable, Semi-stable)
Evaluating different SAT-based search schema
Integrate the proposed approach in the SCC-recursive schema
(encouraging preliminary results!)
Wider empirical investigation

30. References I
[Audemard and Simon, 2009] Audemard, G. and Simon, L. (2009).
Predicting learnt clauses quality in modern sat solvers.
In Proceedings of IJCAI 2009, pages 399–404.
[Audemard and Simon, 2012] Audemard, G. and Simon, L. (2012).
Glucose 2.1.
http://www.lri.fr/~simon/?page=glucose.
[Biere, 2009] Biere, A. (2009).
P{re,ic}osat@sc’09.
In SAT Competition 2009.
[Caminada, 2006] Caminada, M. (2006).
On the issue of reinstatement in argumentation.
In Proceedings of JELIA 2006, pages 111–123.
[Caminada and Gabbay, 2009] Caminada, M. and Gabbay, D. M. (2009).
A logical account of formal argumentation.
Studia Logica (Special issue: new ideas in argumentation theory), 93(2–3):109–145.
[Nofal et al., 2012] Nofal, S., Dunne, P. E., and Atkinson, K. (2012).
On preferred extension enumeration in abstract argumentation.
In Proceedings of COMMA 2012, pages 205–216.