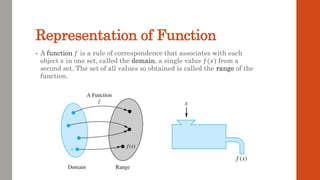
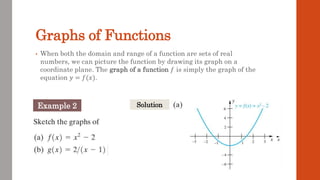
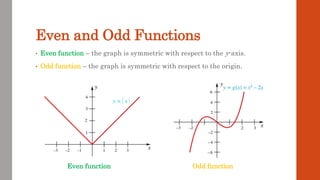
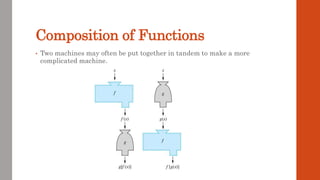
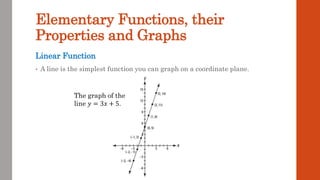
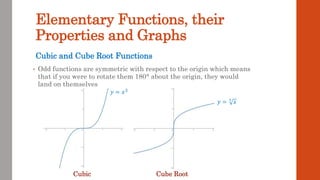
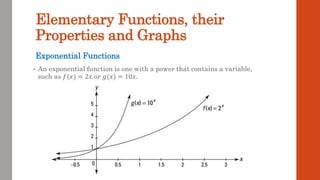
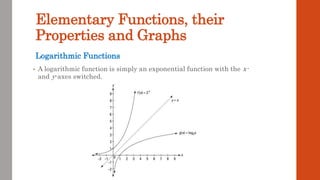
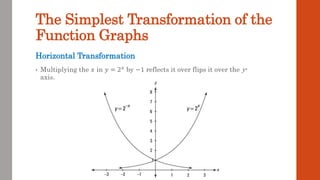
This document discusses functions and their graphs. It defines what a function is and introduces function notation. It discusses the domain and range of a function and how to graph functions on a coordinate plane. It also covers even and odd functions, operations on functions like addition and composition, and finding the inverse of a function. Finally, it discusses elementary functions like linear, quadratic, cubic, exponential and logarithmic functions and how their graphs can be transformed through horizontal and vertical shifts, stretches, flips, and scaling.

1. Functions and their
Graphs
Instr. Eljon Tabulinar

2. Representation of Function
• A function 𝑓 is a rule of correspondence that associates with each
object 𝑥 in one set, called the domain, a single value 𝑓(𝑥) from a
second set. The set of all values so obtained is called the range of the
function.

3. Function Notation
• A single letter like 𝑓 (or 𝑔 or 𝐹) is used to name a function. Then 𝑓 𝑥
read as “f of x” or “f at x,” denotes the value the 𝑓 assigns at 𝑥.
• If 𝑓 𝑥 = 𝑥3 − 4, then
𝑓 2 = 23 − 4 = 4
𝑓 𝑎 = 𝑎3 − 4
𝑓 𝑎 + ℎ = 𝑎 + ℎ 3 − 4
Example 1
Solution

4. Solution
Example 1

5. Domain and Range
• To specify a function completely, we must state, in addition to the
rule of correspondence, the domain of the function. For example, if 𝐹
is the function defined by 𝐹 𝑥 = 𝑥2
+ 1 with domain {−1, 0, 1, 2, 3},
then the range is {1, 2, 5, 10}. The rule of correspondence, together
with the domain, determines the range.

6. Graphs of Functions
• When both the domain and range of a function are sets of real
numbers, we can picture the function by drawing its graph on a
coordinate plane. The graph of a function 𝑓 is simply the graph of the
equation 𝑦 = 𝑓(𝑥).
Example 2 Solution

7. Even and Odd Functions
• Even function – the graph is symmetric with respect to the y-axis.
• Odd function – the graph is symmetric with respect to the origin.
Even function Odd function

8. Even and Odd Functions
• A function 𝑓 is an even function if 𝑓 −𝑥 = 𝑓(𝑥)
• A function 𝑓 is an odd function if 𝑓 −𝑥 = −𝑓(𝑥)
Example 3
Solution
𝑓 is an odd function. The graph of 𝑦 = 𝑓(𝑥) is symmetric
with respect to the origin.

9. Operations on Functions
• Just as two numbers 𝑎 and 𝑏 can be added to produce a new number,
so two functions 𝑓 and 𝑔 can be added to produce a new function 𝑓 + 𝑔.
Sum, Differences, Products, Quotients, and Powers
Consider functions 𝑓 and 𝑔 with formulas
𝑓 𝑥 =
𝑥 − 3
2
𝑔 𝑥 = 𝑥

10. Operations on Functions
• We have to be careful about domains
• We had to exclude 0 from the domain of
𝑓
𝑔
to avoid division of 0.

11. Composition of Functions
• Two machines may often be put together in tandem to make a more
complicated machine.

12. Composition of Function
• If 𝑓 works on 𝑥 to produce 𝑓(𝑥) and 𝑔 then works on 𝑓(𝑥) to produce
𝑔(𝑓(𝑥)), we say that we have composed g with 𝑓. The resulting
function, called the composition of 𝑔 with 𝑓, is denoted by 𝑔 ∘ 𝑓 Thus,

13. Composition of Function
Example 4
Solution
[0,3) ∪ (3, ∞)
Domain

14. Inverse of a Function
• The function 𝑓(𝑥) = 𝑥2 (for 𝑥 ≥ 0) and the function 𝑓−1(𝑥) = 𝑥 (read
as “𝑓 inverse of 𝑥”) are inverse functions because each undoes what
the other does.
• 𝑓 𝑥 and 𝑓−1(𝑥) are inverse functions if and only if 𝑓−1 𝑓(𝑥) = 𝑥 and
𝑓 𝑓−1 𝑥 = 𝑥.

15. Finding the Inverse of a Function
Algebraically
Find the inverse of the following function algebraically.
1. 𝑓 𝑥 = 4 − 4𝑥 2. 𝑓 𝑥 = 𝑥2
− 4𝑥
Example 5
Solution
1. 𝑓 𝑥 = 4 − 4𝑥
First replace 𝑓(𝑥) with 𝑦:
𝑓 𝑥 = 4 − 5𝑥
𝑦 = 4 − 5𝑥
Then replace 𝑦 with 𝑥 and each 𝑥
with 𝑦. After making some
replacements, solve for 𝑦 to find
the inverse:
𝑥 = 4 − 5𝑦
5𝑦 = 4 − 𝑥
𝑦 =
4 − 𝑥
5
Therefore, the inverse of
𝑓 𝑥 = 4 − 5𝑥 is 𝑓−1 𝑥 =
4−𝑥
5

16. Elementary Functions, their
Properties and Graphs
• A line is the simplest function you can graph on a coordinate plane.
Linear Function
The graph of the
line 𝑦 = 3𝑥 + 5.

17. Elementary Functions, their
Properties and Graphs
• Notice that both functions are symmetric with respect to the y-axis.
Parabolic and Absolute Value Functions
Parabolic Absolute Value

18. Elementary Functions, their
Properties and Graphs
• Odd functions are symmetric with respect to the origin which means
that if you were to rotate them 180° about the origin, they would
land on themselves
Cubic and Cube Root Functions
Cubic Cube Root
𝑦 = 𝑥3
𝑦 = 3
𝑥

19. Elementary Functions, their
Properties and Graphs
• An exponential function is one with a power that contains a variable,
such as 𝑓(𝑥) = 2𝑥 or 𝑔(𝑥) = 10𝑥.
Exponential Functions

20. Elementary Functions, their
Properties and Graphs
• A logarithmic function is simply an exponential function with the x-
and y-axes switched.
Logarithmic Functions

21. The Simplest Transformation of the
Function Graphs
• Any function can be transformed into a related function by shifting it
horizontally or vertically, flipping it over horizontally or vertically, or
stretching or shrinking it horizontally or vertically.
• Consider the exponential function 𝑦 = 2𝑥.

22. The Simplest Transformation of the
Function Graphs
Horizontal Transformation
• Adding to 𝑥 makes the function go left, subtracting from 𝑥 makes the
function go right.

23. The Simplest Transformation of the
Function Graphs
Horizontal Transformation
• multiplying 𝑥 by a number greater than 1 shrinks the function, and
multiplying 𝑥 by a number less than 1 expands the function
𝑦 = 2𝑥
𝑦 = 22𝑥
𝑦 = 20.5𝑥

24. The Simplest Transformation of the
Function Graphs
Horizontal Transformation
• Multiplying the 𝑥 in 𝑦 = 2𝑥 by −1 reflects it over flips it over the y-
axis.

25. The Simplest Transformation of the
Function Graphs
Vertical Transformation
• To transform a function vertically, you add a number to or subtract a
number from the entire function or multiply the whole function by a
number. Say, the original function is 𝑦 = 10𝑥
𝑦 = 10𝑥
+ 6 shifts the original function up 6 units.
𝑦 = 10𝑥
− 2 shifts the original function down 2 units.
𝑦 = 5 ∙ 10𝑥 stretches the original function vertically by a factor of 5.
𝑦 =
1
3
∙ 10𝑥 stretches the original function vertically by a factor of 3.