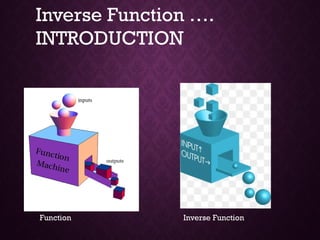
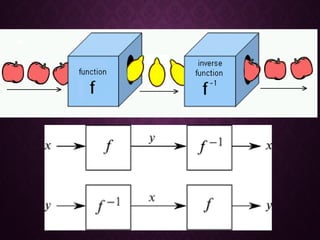
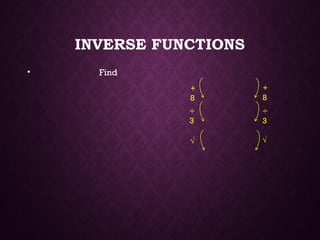
The document discusses inverse functions, introducing key concepts such as how to find the inverse by rearranging equations and how inverse functions 'undo' the original function. It provides examples and exercises, illustrating the concept with various functions and their inverses. Additionally, students are given activities to practice finding and understanding inverse functions.

1. FUNCTIONS
Chapter
21

2. STARTER……
If function f(x) = 3x – 6 then Find:
a f(10) b f(0) c f(6) d f(–6)

3. INVERSE FUNCTIONS
Learning Objectives:
• Able to re-arrange an equation
• Able to find the inverse of a simple function
Grade 10 14/11/2024

4. INVERSE FUNCTIONS (1)
• Today we will be looking at Inverse Functions
• Every operation has an ‘opposite’, for example the opposite of addition is
subtraction
• The inverse of a function is the function that will ‘undo’ it and return you to
the input
• Effectively, you can think of it as a function machine, but in the opposite
order

5. Function Inverse Function
Inverse Function ….
INTRODUCTION

7. INVERSE FUNCTION
• Function f(x)
• Inverse of function f(x) is f-1
(x)

8. Outpu
t
Function
x 2 + 3 17
7 19
8 x
Inverse Functions
How do you think inverse
functions work?
2
3

x

9. INVERSE FUNCTIONS (1)
For simple functions, you can use the idea of a ‘function
machine’
𝑓 (𝑥)=𝑥+7
Input +7 Output
Input -7 Output
𝑓 −1
( 𝑥)=𝑥−7
As a ‘function machine’, f(x)
would look like this
f-1
(x) means ‘the inverse
function of f(x)
𝑔(𝑥)=3 𝑥
Input x3 Output
Input ÷3 Output
𝑔−1
(𝑥 )=
𝑥
3
As a ‘function machine’, g(x)
would look like this
g-1
(x) means ‘the inverse
function of g(x)

10. INVERSE FUNCTIONS
• Consider the function
• Then the inverse function is
𝑥
3 𝑥
𝑓(𝑥)=3𝑥−2
x 3 - 2
𝑓
−1
(𝑥)=
𝑥+2
3
𝑥+2
𝑓(𝑥)=3𝑥−2
÷ 3 + 2
𝑥
f(2) = 3x2 – 2
f (2) = 4
f-1
(4) =
f-1
(4) = 2
3x
𝑥

11. INVERSE FUNCTIONS (1)
For simple functions, you can use the idea of a ‘function
machine’
𝑓 (𝑥 )=
𝑥 +4
2
Input +4 Output
𝑓 −1
(𝑥)=2𝑥 − 4
As a ‘function machine’, f(x)
would look like this
÷2
Input -4 Output
x2
𝑔(𝑥)=5(𝑥+1)
Input +1 Output
𝑔−1
(𝑥 )=
𝑥
5
−1
As a ‘function machine’, g(x)
would look like this
x5
Input -1 Output
÷5

12. INVERSE FUNCTIONS (
• To find the inverse function:
• Set the function equal to
• Re-arrange to make the subject
• Replace the with and with

13. ACTIVITY 1: REARRANGE
INVERSE FUNCTION STEPS
•To find the inverse function:
• Replace the with and with
• Re-arrange to make the subject
• Set the function equal to

14. INVERSE FUNCTIONS
• To find the inverse function:
• Set the function equal to
• Re-arrange to make the subject
• Replace the with and with
• EXAMPLE: + 2 find
1 . y = x + 2
3 . x = y - 2
2 . x + 2 = y
4. f-1(x)
= x- 2

15. FIND F-1
(X)
• To find the inverse function:
• Set the function equal to
• Re-arrange to make the subject
• Replace the with and with
• Y = 4x
• X = y/4
• = x/4

16. FIND F-1
(X)
• To find the inverse function:
• Set the function equal to
• Re-arrange to make the subject
• Replace the with and with
• Y = x/4
• X = 4y
• = 4x

17. INVERSE FUNCTIONS
• To find the inverse function:
• Set the function equal to
• Re-arrange to make the subject
• Replace the with and with
• EXAMPLE: find
x
5
x
5
- 3 - 3
÷
2
÷
2

18. INVERSE FUNCTIONS
• Find
+
8
+
8
÷
3
÷
3
√ √

19. ACTIVITY 2.

20. To A Something Did On Me Yesterday Over called
21 - 3 9 123 - 12 4 0 -56 28
Man Rose Principal How Threw It Happened What Strange
- 1 113 2 30 3 8 --7 19 -5
Functions Code Breaker
Find the value of each of the following functions to find the word to fill in the space in
the joke at the bottom.
.
.
!
a) f(7) b) f(g(2)) c) g(-5) d) g h(5)
e) f-1
(3) f) g-1
(-2) g) h-1
(2) h) f h(4) + 5
i) 2 h(2)
f(x) = 2x-5 g(x) = x-2 h(x) = x2
- 2

21. SUMMARY …..
• We learnt about inverse function…..
• Steps to find inverse of a function………….
• We are able to find inverse of a funtion…..

22. INVERSE FUNCTIONS: HOT..

23. PLENARY

24. H.W.
• Worksheet on google class