Firas Obeidat, profile picture
Uploaded byFiras Obeidat
PDF, PPTX4,592 views

AC AC converters

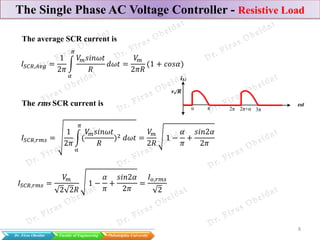
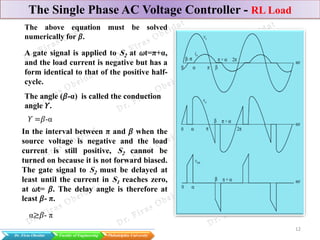
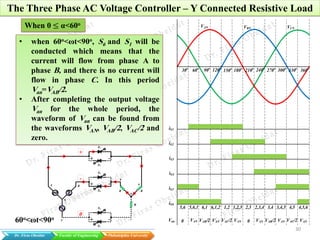
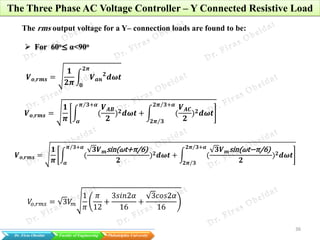
The document discusses various types of AC voltage controllers, specifically focusing on single-phase and three-phase configurations with resistive and RL loads. It details the basic operations, formulas, and calculations necessary for understanding how these converters manage voltage and power delivery. The document includes practical examples, showcasing the application of theoretical concepts in real-world scenarios.

Embed presentation

Download as PDF, PPTX
Power Electronics AC-AC Converters 1 Dr. Firas Obeidat E-mail: firasobeidat@gmail.com fobeidat@philadelphia.edu.jo
2 Table of contents 1 • Introduction 2 • The Single Phase AC Voltage Controller 3 • The Single Phase AC Voltage Controller - Resistive Load 4 • The Single Phase AC Voltage Controller - RL Load 5 • The Three Phase AC Voltage Controller – Y Connected Resistive Load 6 • The Three Phase AC Voltage Controller – Δ Connected Resistive Load Dr. Firas Obeidat Faculty of Engineering Philadelphia University
3 Dr. Firas Obeidat Faculty of Engineering Philadelphia University Introduction An ac voltage controller is a converter that controls the voltage, current, and average power delivered to an ac load from an ac source. The phase-controlled ac voltage controller has several practical uses including light-dimmer circuits and speed control of induction motors. In a switching scheme called phase control, switching takes place during every cycle of the source, in effect removing some of the source waveform before it reaches the load. Integral-cycle control, the source is connected and disconnected for several cycles at a time.
4 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Single Phase AC Voltage Controller Basic Operation For the single phase AC voltage controller shown, electronic switches are shown as parallel thyristors (SCRs). This SCR arrangement makes it possible to have current in either direction in the load. This SCR connection is called antiparallel or inverse parallel because the SCRs carry current in opposite directions. A triac is equivalent to the antiparallel SCRs. Other controlled switching devices can be used instead of SCRs.  Load current contains both positive and negative half-cycles. An analysis identical to that done for the controlled half-wave rectifier can be done on a half cycle for the voltage controller. Then, by symmetry, the result can be extrapolated to describe the operation for the entire period.  S1 conducts if a gate signal is applied during the positive half-cycle of the source. S1 conducts until the current in it reaches zero.  A gate signal is applied to S2 during the negative half-cycle of the source, providing a path for negative load current. vs L o a d + -vsw S1 S2 + - + - io vo
5 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Single Phase AC Voltage Controller Basic Operation Basic observations about this controller The SCRs cannot conduct simultaneously. The load voltage is the same as the source voltage when either SCR is on. The load voltage is zero when both SCRs are OFF. The switch voltage vsw is zero when either SCR is ON and is equal to the source voltage when neither is ON. The average current in the source and load is zero if the SCRs are on for equal time intervals. The average current in each SCR is not zero because of unidirectional SCR current. The rms current in each SCR is 1/√2 times the rms load current if the SCRs are on for equal time intervals.
6 Dr. Firas Obeidat Faculty of Engineering Philadelphia University vs + -vsw S1 S2 + - + - io voR The Single Phase AC Voltage Controller - Resistive Load 𝑣𝑠 𝜔𝑡 = 𝑉𝑚 𝑠𝑖𝑛𝜔𝑡 𝑣𝑠 𝜔𝑡 = 𝑉𝑚 𝑠𝑖𝑛𝜔𝑡 𝛼 < 𝜔𝑡 < 𝜋 𝑎𝑛𝑑 𝜋 + 𝛼 < 𝜔𝑡 < 2𝜋 0 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒 Let the voltage source be Output voltage is The rms load voltage is 𝑉𝑜,𝑟𝑚𝑠 = 1 𝜋 (𝑉𝑚 𝑠𝑖𝑛𝜔𝑡)2 𝑑𝜔𝑡 𝜋 α = 𝑉𝑚 2 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋
7 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - Resistive Load The power factor of the load is The rms current in the load and the source is 𝐼 𝑜,𝑟𝑚𝑠 = 𝑉𝑜,𝑟𝑚𝑠 𝑅 = 𝑉𝑚 𝑅 2 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 𝑝𝑓 = 𝑃 𝑆 = 𝑉𝑜,𝑟𝑚𝑠 2 𝑅 𝑉𝑠,𝑟𝑚𝑠 𝐼𝑠,𝑟𝑚𝑠 = 𝑉𝑜,𝑟𝑚𝑠 2 𝑅 𝑉𝑠,𝑟𝑚𝑠(𝑉𝑜,𝑟𝑚𝑠 𝑅) = 𝑉𝑜,𝑟𝑚𝑠 𝑉𝑠,𝑟𝑚𝑠 = 𝑉𝑚 2 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 𝑉𝑚 2 𝑝𝑓 = 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 The pf=1 for α=0, which is the same as for an uncontrolled resistive load, and the power factor for α>0 is less than 1. The average source current is zero because of half-wave symmetry. 𝐼𝑠,𝐴𝑣𝑔 = 𝐼 𝑜,𝐴𝑣𝑔 = 0
8 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - Resistive Load The average SCR current is 𝐼𝑆𝐶𝑅,𝐴𝑣𝑔 = 1 2𝜋 𝑉𝑚 𝑠𝑖𝑛𝜔𝑡 𝑅 𝑑𝜔𝑡 𝜋 𝛼 = 𝑉𝑚 2𝜋𝑅 (1 + 𝑐𝑜𝑠𝛼) 𝐼𝑆𝐶𝑅,𝑟𝑚𝑠 = 1 2𝜋 ( 𝑉𝑚 𝑠𝑖𝑛𝜔𝑡 𝑅 )2 𝑑𝜔𝑡 𝜋 α = 𝑉𝑚 2𝑅 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 The rms SCR current is 𝐼𝑆𝐶𝑅,𝑟𝑚𝑠 = 𝑉𝑚 2 2𝑅 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 = 𝐼 𝑜,𝑟𝑚𝑠 2 πα 2π 2π+α 3π ωt iS1 vs/R
9 Dr. Firas Obeidat Faculty of Engineering Philadelphia University Example: The single-phase ac voltage controller has a 120-V rms 60-Hz source. The load resistance is 15 Ω. Determine (a) the delay angle required to deliver 500 W to the load, (b) the rms source current, (c) the rms and average currents in the SCRs, (d) the power factor. 𝑉𝑜,𝑟𝑚𝑠 = 𝑉𝑚 2 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 = 2 × 120 2 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 𝑃 = 𝑉𝑜,𝑟𝑚𝑠 2 𝑅 → 𝑉𝑜,𝑟𝑚𝑠 2 = 𝑃𝑅 = 500 × 15 = 7500 𝑉𝑜,𝑟𝑚𝑠 2 = 1202 (1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 ) ∴ 7500 = 14400(1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 ) 𝛼 𝜋 − 𝑠𝑖𝑛2𝛼 2𝜋 = 0.479 2𝛼 − 𝑠𝑖𝑛2𝛼 = 3.01 𝛼 = 1.54 rad = 88.1 𝑜 (a) The Single Phase AC Voltage Controller - Resistive Load
10 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - Resistive Load (b) 𝐼 𝑜,𝑟𝑚𝑠 = 𝑉𝑜,𝑟𝑚𝑠 𝑅 = 86.6 15 = 5.77 A 𝑉𝑜,𝑟𝑚𝑠 2 = 7500 → 𝑉𝑜,𝑟𝑚𝑠 = 86.6From (a) 𝐼𝑆𝐶𝑅,𝐴𝑣𝑔 = 𝑉𝑚 2𝜋𝑅 1 + 𝑐𝑜𝑠𝛼 = 2 × 120 2𝜋15 1 + 𝑐𝑜𝑠88.1 = 1.86 A 𝐼𝑆𝐶𝑅,𝑟𝑚𝑠 = 𝐼 𝑜,𝑟𝑚𝑠 2 = 5.77 2 = 4.08 A (c) 𝑝𝑓 = 𝑃 𝑆 = 𝑃 𝑉𝑠,𝑟𝑚𝑠 𝐼𝑠,𝑟𝑚𝑠 = 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 = 500 120 × 5.77 = 0.722(d)
11 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - RL Load vs + -vsw S1 S2 + - + - io vo R L When a gate signal is applied to S1 at 𝜔t=α in single phase AC voltage controller with RL load, Kirchhoff’s voltage law for the circuit is expressed as. 𝑉𝑚 𝑠𝑖𝑛𝜔𝑡 = 𝑅𝑖 𝑜 𝑡 + 𝐿 𝑑𝑖 𝑜 𝑡 𝑑𝑡 The solution for current in this equation (as obtained in the controlled half wave rectifier section) is 𝑖 𝑜 𝜔𝑡 = 𝑉𝑚 𝑍 sin 𝜔𝑡 − 𝜃 − sin(𝛼 − 𝜃)𝑒(𝛼−𝜔𝑡) 𝜔𝜏 𝛼 ≤ 𝜔𝑡 ≤ 𝛽 0 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒 where 𝑍 = 𝑅2 + (𝜔𝐿)2 𝜃 = 𝑡𝑎𝑛−1 ( 𝜔𝐿 𝑅 ) The extinction angle 𝛽 is the angle at which the current returns to zero, when 𝜔𝑡= 𝛽, 𝑖 𝑜 𝛽 = 𝑉𝑚 𝑍 sin 𝛽 − 𝜃 − sin(𝛼 − 𝜃)𝑒(𝛼−𝛽) 𝜔𝜏 (1) (2)
12 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - RL Load A gate signal is applied to S2 at 𝜔t=π+α, and the load current is negative but has a form identical to that of the positive half- cycle. The above equation must be solved numerically for 𝛽. The angle (𝛽-α) is called the conduction angle 𝛶. 𝛶 =𝛽-α In the interval between π and 𝛽 when the source voltage is negative and the load current is still positive, S2 cannot be turned on because it is not forward biased. The gate signal to S2 must be delayed at least until the current in S1 reaches zero, at 𝜔t= 𝛽. The delay angle is therefore at least 𝛽- π. α≥𝛽- π
13 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - RL Load When α=θ, equation (2) becomes sin 𝛽 − 𝜃 = 0 which has a solution 𝛽 − 𝜃 = π Therefore 𝛶 = 𝜋 When α=θ When 𝛶=𝜋, one SCR is always conducting, and the voltage across the load is the same as the voltage of the source. The load voltage and current are sinusoids for this case, and the circuit is analyzed using phasor analysis for AC circuits. The power delivered to the load is continuously controllable between the two extremes corresponding to full source voltage and zero. The expression of rms load current is 𝐼 𝑜,𝑟𝑚𝑠 = 1 𝜋 𝑖 𝑜 2 (𝜔𝑡) 𝑑𝜔𝑡 𝛽 α = 1 𝜋 𝑉 𝑚 𝑍 sin 𝜔𝑡 − 𝜃 − 𝑉 𝑚 𝑍 sin(𝛼 − 𝜃)𝑒(𝛼−𝜔𝑡) 𝜔𝜏 2 𝑑𝜔𝑡 𝛽 α
14 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - RL Load The average output voltage can be found as An other way to find the expression of rms load current is 𝐼 𝑜,𝑟𝑚𝑠 = 1 𝑅2 + (𝜔𝐿)2 𝑉𝑚 2 1 𝜋 (𝛽 − 𝛼 − 1 2 𝑠𝑖𝑛2𝛽 + 1 2 𝑠𝑖𝑛2𝛼) Power absorbed by the load is determined from 𝑃 = 𝐼 𝑜,𝑟𝑚𝑠 2 𝑅 The power factor of the load is 𝑝𝑓 = 𝑃 𝑆 = 𝑉𝑜,𝑟𝑚𝑠 𝐼 𝑜,𝑟𝑚𝑠 𝑉𝑠,𝑟𝑚𝑠 𝐼𝑠,𝑟𝑚𝑠 = 𝑉𝑜,𝑟𝑚𝑠 𝑉𝑠,𝑟𝑚𝑠 = 1 𝜋 (𝛽 − 𝛼 − 1 2 𝑠𝑖𝑛2𝛽 + 1 2 𝑠𝑖𝑛2𝛼) 𝑉𝑜,𝑟𝑚𝑠 = 1 𝜋 (𝑉𝑚 𝑠𝑖𝑛𝜔𝑡)2 𝑑𝜔𝑡 𝛽 α = 𝑉𝑚 2 1 𝜋 (𝛽 − 𝛼 − 1 2 𝑠𝑖𝑛2𝛽 + 1 2 𝑠𝑖𝑛2𝛼)
15 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - RL Load Each SCR carries one-half of the current waveform, making the average SCR current 𝐼𝑆𝐶𝑅,𝐴𝑣𝑔 = 1 2𝜋 𝑖 𝑜(𝜔𝑡) 𝑑𝜔𝑡 𝛽 α = 1 2𝜋 𝑉𝑚 𝑍 sin 𝜔𝑡 − 𝜃 − sin(𝛼 − 𝜃)𝑒(𝛼−𝜔𝑡) 𝜔𝜏 𝑑𝜔𝑡 𝛽 α The rms current in each SCR is 𝐼𝑆𝐶𝑅,𝑟𝑚𝑠 = 𝐼 𝑜,𝑟𝑚𝑠 2 The average load current is zero, 𝐼 𝑜,𝐴𝑣𝑔 = 0
16 Dr. Firas Obeidat Faculty of Engineering Philadelphia University Example: For the single-phase voltage controller with RL load, the source is 120Vrms at 60 Hz, and the load is a series RL combination with R=20Ω and L=50mH. The delay angle α is 90. Determine (a) an expression for load current for the first half-period, (b) the rms load current, (c) the rms SCR current, (d) the average SCR current, (e) the power delivered to the load, and (f) the power factor. (a) The Single Phase AC Voltage Controller - RL Load The extinction angle is determined from the numerical solution of i(β)=0 in the above equation.
17 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - RL Load (b) (c) (d) (e) (f) 𝐼 𝑜,𝑟𝑚𝑠 = 1 27.5 × 120 × 1 𝜋 (3.83 − 1.57 − 1 2 𝑠𝑖𝑛440 + 0) = 3.27 A 𝐼 𝑜,𝑟𝑚𝑠 = 1 𝑅2 + (𝜔𝐿)2 𝑉𝑚 2 1 𝜋 (𝛽 − 𝛼 − 1 2 𝑠𝑖𝑛2𝛽 − 1 2 𝑠𝑖𝑛2𝛼) Or
18 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load  The power delivered to the load in three phase AC voltage controller with Y-connected resistive load is controlled by the delay angle α on each thyristor. The six thyristors are turned on in the sequence 1-2- 3-4-5-6, at 60 intervals. Gate signals are maintained throughout the possible conduction angle. + - S4 S1 + - S6 S3 + - S2 S5 A B C ab c R RR n N  The instantaneous voltage across each phase of the load is determined by which thyristors are conducting. At any instant, three thyristors , two thyristors , or no thyristors are ON.  The instantaneous load voltages are either a line-to-neutral voltage (three thyristors ON), one-half of a line-to-line voltage (two thyristors ON), or zero (none on).  Which thyristors are conducting depends on the delay angle α and on the source voltages at a particular instant. The ranges of α that produce particular types of load voltages are 0< α<60o, 60o< α<90o and 90o< α<150o.
19 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o  To study the output voltage Van, Vbn and Vcn, triggering angle α must be determined first.  Suppose that the triggering angle α equal to 30o.  The output voltage Van will be studies when α= 30o, and the same procedure can be applied to get the output voltages Vbn and Vcn at any triggering angle from 0 to 60o. 𝑉𝐴𝑁 = 𝑉𝑚sin𝜔t 𝑉𝐵𝑁 = 𝑉𝑚sin(𝜔t-2π/3) 𝑉𝐶𝑁 = 𝑉𝑚sin(𝜔t-4π/3) Let 𝑉𝐴𝐵 = 3𝑉𝑚sin(𝜔t+π/6) 𝑉𝐵𝐶 = 3𝑉𝑚sin(𝜔t-π/2) 𝑉𝐶𝐴 = 3𝑉𝑚sin(𝜔t-7π/6) VAN VBN VCN 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o
20 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o 1. Determine the triggering angle α (for example α= 30o). 2. Determine the conducting period for each thyristor. • As seen from the input phase voltages VAN, VBN and VCN, every 30o there is a change that affect on the conduction of each thyristor. VAN VBN VCN 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o VAN=VCN VCN=0 VBN=0 VAN=VBN VAN=0 VCN=0 VBN=VCN VBN=0 VAN=0 VAN=VBNVAN=VCNVBN=VCN
21 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o VAN VBN VCN iG1 iG6 iG5 iG4 iG3 iG2 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o • Because α=30o, S1 will be triggered at 30o, S3 will be triggered at 150o (120o+α), S5 will be triggered at 270o (240o+α). • S4 will be triggered after S1 by 180o, S6 will be triggered after S3 by 180o S2 will be triggered after S5 by 180o. • The six SCRs are turned on in the sequence 1-2-3-4-5-6, at 60o intervals. + - S4 S1 + - S6 S3 + - S2 S5 A B C ab c R RR n N
22 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o 3. Study the conduction period for each thyristor. • Each thyristor will be studied at each angle that affect on the conduction of each thyristor to determine if the thyristor will conduct or not. • The conduction period will be studied for S1. • At 30o, VAN=VCN, VAN and VCN are positive, while VBN is negative. So, the current will flow from phase A and C to phase B. S1 will be on from 30o to 60o. VAN VBN VCN iG1 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o + - S4 S1 + - S6 S3 + - S2 S5 A B C a b c R RR n N + + -
23 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o • At 60o, VCN=0, VAN is positive, while VBN is negative. So, the current will flow from phase Ato phase B. S1 will be ON from 60o to 90o. VAN VBN VCN iG1 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o + - S4 S1 + - S6 S3 + - S2 S5 A B C a b c R RR n N + 0 -
24 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o • At 90o, VBN=VCN, VAN is positive, while VBN and VCN are negative. So, the current will flow from phase Ato phase B and phase C. S1 will be ON from 90o to 120o. + - S4 + - S6 S3 + - S2 S5 A B C a b c R RR n N + - - VAN VBN VCN iG1 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o
25 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o • At 120o, VBN=0, VAN is positive, while VCN is negative. So, the current will flow from phase Ato phase C. S1 will be ON from 120o to 150o. + - S4 S1 + - S6 S3 + - S2 S5 A B C a b c R RR n N + 0 - VAN VBN VCN iG1 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o
26 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o • At 150o, VAN=VBN, VAN and VBN are positive, VCN is negative. So, the current will flow from phase A and B to phase C. S1 will be ON from 150o to 180o. + - S4 S1 + - S6 S3 + - S2 S5 A B C a b c R RR n N + + - VAN VBN VCN iG1 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o
27 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o • At 180o, VAN=0, VBN is positive, VCN is negative. So, the current will flow from phase B to phase C and the current will not flow in phase A. S1 will be OFF from 180o to 210o. • At 210o, VAN= VCN, VBN is positive, VAN and VCN are negative. So, the current will flow from phase B to phase A and C. S1 will be OFF from 210o to 240o. • At 240o, VCN= 0, VBN is positive, VAN is negative. So, the current will flow from phase B to phase A. S1 will be OFF from 240o to 270o. • At 270o, VBN=VCN, VBN and VCN are positive, VAN is negative. So, the current will flow from phase B and C to phase A. S1 will be OFF from 270o to 300o. • At 300o, VBN=0, VCN is positive, VAN is negative. So, the current will flow from phase C to phase A. S1 will be OFF from 300o to 330o. • At 330o, VAN=VBN, VCN is positive, VAN and VBN are negative. So, the current will flow from phase C to phase A and B. S1 will be OFF from 330o to 360o.
28 Dr. Firas Obeidat Faculty of Engineering Philadelphia University • The same procedure can be done for other thyristors to determine the conduction period for each thyristor. 4. Determine the thyristors that will be conducted for each period. For example, when 0<ωt<30o, S5 and S6 will be conducted, when 30o<ωt<60o, S5, S6 and S1 will be conducted, ect… VAN VBN VCN iG1 iG6 iG5 iG4 iG3 iG2 6,1,2 2,3,41,2,36,1 2,31,2 3,4 3,4,5 4,5 4,5,65,6 5,6,1 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o
29 Dr. Firas Obeidat Faculty of Engineering Philadelphia University 5. Determine the output voltages (Van, Vbn and Vcn) at each period. • The output voltage Van can be found by applying the thyristors that will be conducted at each period. • when 0<ωt<30o, S5 and S6 will be conducted which means that the current will flow from phase C to phase B, and there is no current will flow in phase A. In this period Van=0. • when 30o<ωt<60o, S5, S6 and S1 will be conducted which means that the current will flow from phase A and C to phase B. In this period Van=VAN. The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o + - S4 S1 + - S6 S3 + - S2 S5 A B C a b c R RR n N 0 + - + - S4 S1 + - S6 S3 + - S2 S5 A B C a b c R RR n N + + - 0<ωt<30o 30o<ωt<60o
30 Dr. Firas Obeidat Faculty of Engineering Philadelphia University • when 60o<ωt<90o, S6 and S1 will be conducted which means that the current will flow from phase A to phase B, and there is no current will flow in phase C. In this period Van=VAB/2. • After completing the output voltage Van for the whole period, the waveform of Van can be found from the waveforms VAN, VAB/2, VAC/2 and zero. The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o + - S4 S1 + - S6 S3 + - S2 S5 A B C a b c R RR n N + 0 - 60o<ωt<90o VAN VBN VCN iG1 iG6 iG5 iG4 iG3 iG2 6,1,2 2,3,41,2,36,1 2,31,2 3,4 3,4,5 4,5 4,5,65,6 5,6,1 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o 0 VAN VAB/2 VAN VAC/2 VAN 0 VAN VAB/2 VAN VAC/2 VANVan
31 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o VAN VBN VCN iG1 iG6 iG5 iG4 iG3 iG2 6,1,2 2,3,41,2,36,1 2,31,2 3,4 3,4,5 4,5 4,5,65,6 5,6,1 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o 0 VAN VAB/2 VAN VAC/2 VAN 0 VAN VAB/2 VAN VAC/2 VANVan VAB/2 VAN VAC/2 Van  The figure below shows the final shape for the output voltage Van. The rms voltage for this waveform will be less than the rms voltage for the input voltages VAN, VBN and VCN. 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o Van 360o
32 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o  The other output waveforms (Vbn and Vcn) can be found by the same way, and the resulting waveform of Vbn will be the same as the waveform of Van shifted by 120o, and the waveform of Vbn will be the same as the waveform of Van shifted by 240o.  At any instant, three thyristors or two thyristors are ON. The instantaneous load voltages are either a line-to-neutral voltage (three thyristors ON), one-half of a line-to-line voltage (two thyristors ON), or zero (none ON)  Because the load is resistive load, the shape of the output current is similar to the shape of the output voltage.
33 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 60o ≤ α<90o  Only two thyristors conduct at any one time when the delay angle is between 60o and 90o.  For α=75o , prior to 75o, S5 and S6 are conducting, and Van=0. When S1 is turned on at 75o, S6 continues to conduct, but S5 must turn off because VCN is negative. Voltage Van is then VAB/2. When S2 is turned on at 135 , S6 is forced off, and Van= VAC/2. The next thyristor to turn on is S3, which forces S1 off, and Van=0. One thyristor is always forced off when thyristor is turned on for α in this range. Load voltages are one-half line-to-line voltages or zero.
34 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 90o ≤ α<150o  Only two thyristors conduct at any one time when the delay angle is between 90o and 150o.  For α=120o , prior to 120o, no thyristors are on, and Van=0. At α=120o, S1 is turned on at 120o, S6 still has a gate signal applied. Since VAB is positive, both S1 and S6 are forward- biased and begin to conduct, and Van=VAB/2. Both S1 and S6 turn off when VAB becomes negative. When a gate signal is applied to S2, it turns on, and S1 turns on again. For α>150o, there is no time interval when thyristor is forward-biased while a gate signal is applied. Output voltage is zero for this condition.
35 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load The rms output voltage for a Y– connection loads are found to be:  For 0o≤ α<60o 𝑽 𝒐,𝒓𝒎𝒔 = 𝟑𝑽 𝒎 𝟏 𝝅 𝝅 𝟔 − 𝜶 𝟒 + 𝒔𝒊𝒏𝟐𝜶 𝟖 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝟐𝝅 𝑽 𝒂𝒏 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟎 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝝅 𝑽 𝑨𝑵 𝟐 𝒅𝝎𝒕 𝝅 𝟑 𝜶 + ( 𝑽 𝑨𝑩 𝟐 ) 𝟐 𝒅𝝎𝒕 𝝅 𝟑+𝜶 𝝅 𝟑 + 𝑽 𝑨𝑵 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟑 𝝅 𝟑+𝜶 + ( 𝑽 𝑨𝑪 𝟐 ) 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟑+𝜶 𝟐𝝅 𝟑 + 𝑽 𝑨𝑵 𝟐 𝒅𝝎𝒕 𝝅 𝟐𝝅 𝟑+𝜶 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝝅 (𝑽 𝒎sin𝜔t ) 𝟐 𝒅𝝎𝒕 𝝅 𝟑 𝜶 + ( 𝟑𝑽 𝒎sin(𝜔t+π/6) 𝟐 ) 𝟐 𝒅𝝎𝒕 𝝅 𝟑+𝜶 𝝅 𝟑 + (𝑽 𝒎sin𝜔t ) 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟑 𝝅 𝟑+𝜶 + ( 𝟑𝑽 𝒎sin(𝜔t−π/6) 𝟐 ) 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟑+𝜶 𝟐𝝅 𝟑 + (𝑽 𝒎sin𝜔t ) 𝟐 𝒅𝝎𝒕 𝝅 𝟐𝝅 𝟑+𝜶
36 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load The rms output voltage for a Y– connection loads are found to be:  For 60o≤ α<90o 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝟐𝝅 𝑽 𝒂𝒏 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟎 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝝅 ( 𝑽 𝑨𝑩 𝟐 ) 𝟐 𝒅𝝎𝒕 𝝅 𝟑+𝜶 𝜶 + ( 𝑽 𝑨𝑪 𝟐 ) 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟑+𝜶 𝟐𝝅 𝟑 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝝅 ( 𝟑𝑽 𝒎sin(𝜔t+π/6) 𝟐 ) 𝟐 𝒅𝝎𝒕 𝝅 𝟑+𝜶 𝜶 + ( 𝟑𝑽 𝒎sin(𝜔t−π/6) 𝟐 ) 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟑+𝜶 𝟐𝝅 𝟑 𝑉𝑜,𝑟𝑚𝑠 = 3𝑉𝑚 1 𝜋 𝜋 12 + 3𝑠𝑖𝑛2𝛼 16 + 3𝑐𝑜𝑠2𝛼 16
37 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load The rms output voltage for a Y– connection loads are found to be:  For 90o≤ α<150o 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝟐𝝅 𝑽 𝒂𝒏 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟎 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝝅 ( 𝑽 𝑨𝑩 𝟐 ) 𝟐 𝒅𝝎𝒕 𝟓𝝅 𝟔 𝜶 + ( 𝑽 𝑨𝑪 𝟐 ) 𝟐 𝒅𝝎𝒕 𝟕𝝅 𝟔 𝝅 𝟑+𝜶 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝝅 ( 𝟑𝑽 𝒎sin(𝜔t+π/6) 𝟐 ) 𝟐 𝒅𝝎𝒕 𝟓𝝅 𝟔 𝜶 + ( 𝟑𝑽 𝒎sin(𝜔t−π/6) 𝟐 ) 𝟐 𝒅𝝎𝒕 𝟕𝝅 𝟔 𝝅 𝟑+𝜶 𝑽 𝒐,𝒓𝒎𝒔 = 𝟑𝑽 𝒎 𝟏 𝝅 𝟓𝝅 𝟐𝟒 − 𝜶 𝟒 + 𝒔𝒊𝒏𝟐𝜶 𝟏𝟔 − 𝟑𝒄𝒐𝒔𝟐𝜶 𝟏𝟔
38 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load Example: a three phase bidirectional AC voltage controller Y-connected connected to resistive load (R=10Ω). The supply voltage VL-L=208V, f=60Hz. If α=π/6, find the output voltage rms value and the input power factor. 𝑉𝑜,𝑟𝑚𝑠 = 3𝑉𝑚 1 𝜋 𝜋 6 − 𝛼 4 + 𝑠𝑖𝑛2𝛼 8 = 208 1 𝜋 𝜋 6 − π/6 4 + 𝑠𝑖𝑛2π/6 8 = 83𝑉 𝐼 𝑜,𝑟𝑚𝑠 = 𝑉𝑜,𝑟𝑚𝑠 𝑅 = 83 10 = 8.3𝐴 𝑃𝑜,𝑎𝑐 = 3𝐼 𝑜,𝑟𝑚𝑠 2 𝑅 = 3 × 8.32 × 10 = 2066.7𝑊 𝑆 = 3𝐼 𝑜,𝑟𝑚𝑠 𝑉𝑖𝑛𝑝𝑢𝑡,𝑟𝑚𝑠 = 3 × 8.3 × 84.9 = 2114.4𝑉𝐴 𝑉𝑖𝑛𝑝𝑢𝑡,𝑟𝑚𝑠 = 208 2 3 = 84.9𝑉 𝑝𝑓 = 𝑃𝑜,𝑎𝑐 𝑆 = 2066.7 2114.4 = 0.977
39 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Δ Connected Resistive Load  The voltage across a load resistor is the corresponding line-to-line voltage when a thyristor in the phase is on. The delay angle is referenced to the zero crossing of the line-to-line voltage. thyristors are turned on in the sequence 1-2-3-4-5-6. The line current in each phase is the sum of two of the delta currents:
40 Dr. Firas Obeidat Faculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Δ Connected Resistive Load The relationship between rms line and delta currents depends on the conduction angle of the thyristors. For small conduction angles (large α), the delta currents do not overlap, and the rms line currents are Current waveforms for α=130o For large conduction angles (small α), the delta currents overlap, and the rms line current is larger than √2IΔ. In the limit when γ (α=0), the delta currents and line currents are sinusoids. The rms line current is determined from ordinary three- phase analysis. Current waveforms for α=90o The range of rms line current is therefore depending on α
41

More Related Content

PPT
chapter4 DC to AC Converter.ppt
byLiewChiaPing
 
PPTX
Unit-5 AC-AC Cycloconverter
byjohny renoald
 
PPT
Three phase-controlled-rectifiers
byTejas Deshpande
 
PPTX
Single phase ac voltage controller
bySwati Tiwari
 
PPTX
Unit-2 Three Phase controlled converter
byjohny renoald
 
PPT
Dc Choppers
bystooty s
 
PDF
Chapter 5 - DC-AC Conversion.pdf
bybenson215
 
PDF
Lecture slides_Ch 8 power electronics daniel hart.pdf
byGIFT University, Gujranwala, Pakistan
 
chapter4 DC to AC Converter.ppt
byLiewChiaPing
 
Unit-5 AC-AC Cycloconverter
byjohny renoald
 
Three phase-controlled-rectifiers
byTejas Deshpande
 
Single phase ac voltage controller
bySwati Tiwari
 
Unit-2 Three Phase controlled converter
byjohny renoald
 
Dc Choppers
bystooty s
 
Chapter 5 - DC-AC Conversion.pdf
bybenson215
 
Lecture slides_Ch 8 power electronics daniel hart.pdf
byGIFT University, Gujranwala, Pakistan
 

What's hot

PPT
Cycloconverter ppt
bySAMUEL-AGI SATURDAY, MIASP,SMIEEE,OSHAcademy [USA].
 
PPTX
Unit- 3 DC-DC Converter
byjohny renoald
 
PPT
Dual converters (1)
byKarthiKeyani10
 
PPTX
DC DC Converter
byMengstu Fentaw
 
PPTX
Single Phase Converter
byVinod Srivastava
 
PPTX
Inverters (DC-AC)
byTaimur Ijaz
 
PPTX
Different methods of pwm for inverter control
byTushar Pandagre
 
PPTX
Current mirror
byHossam Moghrabi
 
PPTX
Synchronous machines
byMohammed Waris Senan
 
PPTX
What is variable frequency drive & how it works
byEngineering Garage V=ir
 
PPTX
1-ф to 1-ф Cycloconverter ppt
byUtsav Yagnik
 
PPTX
Power MOSFET
byjohny renoald
 
PPTX
speed control of three phase induction motor
byAshvani Shukla
 
POTX
Sinusoidal pwm
byChintan Hansalia
 
PPTX
Voltage Source Inverter
byPreetamJadhav2
 
PPTX
Differential Protection Relay
bykishore kish
 
PPTX
Facts devices
byVinod Srivastava
 
PPT
Three phase ac voltage controllers
byJosin Hippolitus
 
PPTX
Ic voltage regulators
byAnita Thattil
 
PDF
dc to dc-converter
byStudent
 
Cycloconverter ppt
bySAMUEL-AGI SATURDAY, MIASP,SMIEEE,OSHAcademy [USA].
 
Unit- 3 DC-DC Converter
byjohny renoald
 
Dual converters (1)
byKarthiKeyani10
 
DC DC Converter
byMengstu Fentaw
 
Single Phase Converter
byVinod Srivastava
 
Inverters (DC-AC)
byTaimur Ijaz
 
Different methods of pwm for inverter control
byTushar Pandagre
 
Current mirror
byHossam Moghrabi
 
Synchronous machines
byMohammed Waris Senan
 
What is variable frequency drive & how it works
byEngineering Garage V=ir
 
1-ф to 1-ф Cycloconverter ppt
byUtsav Yagnik
 
Power MOSFET
byjohny renoald
 
speed control of three phase induction motor
byAshvani Shukla
 
Sinusoidal pwm
byChintan Hansalia
 
Voltage Source Inverter
byPreetamJadhav2
 
Differential Protection Relay
bykishore kish
 
Facts devices
byVinod Srivastava
 
Three phase ac voltage controllers
byJosin Hippolitus
 
Ic voltage regulators
byAnita Thattil
 
dc to dc-converter
byStudent
 

Similar to AC AC converters

PPT
l4-ac-ac converters.ppt
byantexnebyu
 
PPTX
Power Electronics - Phase Controlled Converters.pptx
byPoornima D
 
PPTX
AC to ac Converters.pptx
byMahmoudMustafa84
 
PDF
Chapter 6 AC-AC Converters.pdf
byLiewChiaPing
 
PDF
Chapter 3 Controlled Rectifier.pdf
byLiewChiaPing
 
PDF
Ch1 AC voltage controllers_Part 3 (1).pdf
bychauhangopal7354
 
PDF
LECTURE on power electronics for every one
byabdalla01062157570
 
PDF
electrical-engineering_engineering_power-electronics_controlled-rectifiers_no...
byLucasMogaka
 
PDF
Ac-chooper or regulators.pdf Power systems
by2400801250
 
PPTX
Half Wave Controlled Rectifier With R-Load-1.pptx
bySuhas Patil
 
DOCX
Bridge rectifier
byDenis Simiyu
 
PPTX
Half Wave Controlled Rectifier with Resistive Load.pptx
bySuhas Patil
 
PPTX
Lecture4 Controlled AC-DC Rectification-Single-Phase -.pptx
byssuserc13700
 
PPTX
Controlled Rectifier with -RL Load-2.pptx
bySuhas Patil
 
PPT
PE (Beta) Chapter AC-AC power converter-slide.ppt
byNurazlinBtMohdYaakop
 
PDF
ac voltage controllers.pdf, Power systems
by2400801250
 
PDF
Ac/AC conveter
byNourhan Selem Salm
 
PDF
AC-DC Converter_a.pdf
byBishnu Prasad Muni
 
PPT
6067793.ppt
byVijay Patil
 
PDF
Performance analysis of a single phase ac voltage controller under induction ...
byeSAT Publishing House
 
l4-ac-ac converters.ppt
byantexnebyu
 
Power Electronics - Phase Controlled Converters.pptx
byPoornima D
 
AC to ac Converters.pptx
byMahmoudMustafa84
 
Chapter 6 AC-AC Converters.pdf
byLiewChiaPing
 
Chapter 3 Controlled Rectifier.pdf
byLiewChiaPing
 
Ch1 AC voltage controllers_Part 3 (1).pdf
bychauhangopal7354
 
LECTURE on power electronics for every one
byabdalla01062157570
 
electrical-engineering_engineering_power-electronics_controlled-rectifiers_no...
byLucasMogaka
 
Ac-chooper or regulators.pdf Power systems
by2400801250
 
Half Wave Controlled Rectifier With R-Load-1.pptx
bySuhas Patil
 
Bridge rectifier
byDenis Simiyu
 
Half Wave Controlled Rectifier with Resistive Load.pptx
bySuhas Patil
 
Lecture4 Controlled AC-DC Rectification-Single-Phase -.pptx
byssuserc13700
 
Controlled Rectifier with -RL Load-2.pptx
bySuhas Patil
 
PE (Beta) Chapter AC-AC power converter-slide.ppt
byNurazlinBtMohdYaakop
 
ac voltage controllers.pdf, Power systems
by2400801250
 
Ac/AC conveter
byNourhan Selem Salm
 
AC-DC Converter_a.pdf
byBishnu Prasad Muni
 
6067793.ppt
byVijay Patil
 
Performance analysis of a single phase ac voltage controller under induction ...
byeSAT Publishing House
 

Recently uploaded

PDF
Lec1a-infinite square well-particle in a box.pdf
byb17052006bhuvanasent
 
PPTX
Amperes Circuital Law and its appliocations
byKasiselvanathanMarim1
 
PDF
Non-Deterministic Finite Automata (NFA) to Deterministic Finite Automata (DFA...
byNileshPardeshi28
 
PDF
Finite Automata With Output - Moore and Mealy Machines definitions and Solved...
byNileshPardeshi28
 
PDF
Yes, we put AI agents in production. No, don't try this at home
byMarie-Alice Blete
 
PPTX
Why Hydraulic Flushing Should Never Be Skipped Before Commissioning
byNeometrix_Engineering_Pvt_Ltd
 
PPTX
CFP_Unit 4. Arrays, Structure and Pointers pptx
bypawarbhaktiit
 
PDF
TrakSYS Certified Engineer Certificate.pdf
byDjordje Zivanovic
 
PDF
Autonomous Talent Systems | Cerebraix Technologies
byCerebraix Technologies
 
PPTX
CFP_Unit 5. Structure and Functions pptx
bypawarbhaktiit
 
PPTX
Solar PV An Essential Requirement in renewable energy based sources Industria...
byshilpashukla2025
 
PPTX
Unit II Introduction to C programming ppts
bypawarbhaktiit
 
PPTX
OPGW-Optical-Ground-Wire-Deployment-Process.pptx
byPrinceBoateng59
 
PPTX
PEMET 413-COMPOSITE MATERIALS-2024 SCHEME-MOD1 LECTURE 5.pptx
byVINAY B
 
PPT
5.1 Basic concept and hierarchy.ppt1234564
byChetansingh768231
 
PPTX
Mathematics in Disaster Management school project
byvsneha2514
 
PPT
Smart waste management using internet of things 2025.ppt
byJeganKalaimani
 
PPTX
plastic road.pptxPlastic Roads: A Sustainable Solution
byalfiyasutar10
 
PPTX
GDG I²IT Freshers' Tech Kickoff Event, Pune
byshahvaibhavi221
 
PPT
software-security-intro Secure software Design and Development
bysahar62648
 
Lec1a-infinite square well-particle in a box.pdf
byb17052006bhuvanasent
 
Amperes Circuital Law and its appliocations
byKasiselvanathanMarim1
 
Non-Deterministic Finite Automata (NFA) to Deterministic Finite Automata (DFA...
byNileshPardeshi28
 
Finite Automata With Output - Moore and Mealy Machines definitions and Solved...
byNileshPardeshi28
 
Yes, we put AI agents in production. No, don't try this at home
byMarie-Alice Blete
 
Why Hydraulic Flushing Should Never Be Skipped Before Commissioning
byNeometrix_Engineering_Pvt_Ltd
 
CFP_Unit 4. Arrays, Structure and Pointers pptx
bypawarbhaktiit
 
TrakSYS Certified Engineer Certificate.pdf
byDjordje Zivanovic
 
Autonomous Talent Systems | Cerebraix Technologies
byCerebraix Technologies
 
CFP_Unit 5. Structure and Functions pptx
bypawarbhaktiit
 
Solar PV An Essential Requirement in renewable energy based sources Industria...
byshilpashukla2025
 
Unit II Introduction to C programming ppts
bypawarbhaktiit
 
OPGW-Optical-Ground-Wire-Deployment-Process.pptx
byPrinceBoateng59
 
PEMET 413-COMPOSITE MATERIALS-2024 SCHEME-MOD1 LECTURE 5.pptx
byVINAY B
 
5.1 Basic concept and hierarchy.ppt1234564
byChetansingh768231
 
Mathematics in Disaster Management school project
byvsneha2514
 
Smart waste management using internet of things 2025.ppt
byJeganKalaimani
 
plastic road.pptxPlastic Roads: A Sustainable Solution
byalfiyasutar10
 
GDG I²IT Freshers' Tech Kickoff Event, Pune
byshahvaibhavi221
 
software-security-intro Secure software Design and Development
bysahar62648
 

AC AC converters

  • 1.
    Power Electronics AC-AC Converters 1 Dr.Firas Obeidat E-mail: firasobeidat@gmail.com fobeidat@philadelphia.edu.jo
  • 2.
    2 Table of contents 1 •Introduction 2 • The Single Phase AC Voltage Controller 3 • The Single Phase AC Voltage Controller - Resistive Load 4 • The Single Phase AC Voltage Controller - RL Load 5 • The Three Phase AC Voltage Controller – Y Connected Resistive Load 6 • The Three Phase AC Voltage Controller – Δ Connected Resistive Load Dr. Firas Obeidat Faculty of Engineering Philadelphia University
  • 3.
    3 Dr. Firas ObeidatFaculty of Engineering Philadelphia University Introduction An ac voltage controller is a converter that controls the voltage, current, and average power delivered to an ac load from an ac source. The phase-controlled ac voltage controller has several practical uses including light-dimmer circuits and speed control of induction motors. In a switching scheme called phase control, switching takes place during every cycle of the source, in effect removing some of the source waveform before it reaches the load. Integral-cycle control, the source is connected and disconnected for several cycles at a time.
  • 4.
    4 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Single Phase AC Voltage Controller Basic Operation For the single phase AC voltage controller shown, electronic switches are shown as parallel thyristors (SCRs). This SCR arrangement makes it possible to have current in either direction in the load. This SCR connection is called antiparallel or inverse parallel because the SCRs carry current in opposite directions. A triac is equivalent to the antiparallel SCRs. Other controlled switching devices can be used instead of SCRs.  Load current contains both positive and negative half-cycles. An analysis identical to that done for the controlled half-wave rectifier can be done on a half cycle for the voltage controller. Then, by symmetry, the result can be extrapolated to describe the operation for the entire period.  S1 conducts if a gate signal is applied during the positive half-cycle of the source. S1 conducts until the current in it reaches zero.  A gate signal is applied to S2 during the negative half-cycle of the source, providing a path for negative load current. vs L o a d + -vsw S1 S2 + - + - io vo
  • 5.
    5 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Single Phase AC Voltage Controller Basic Operation Basic observations about this controller The SCRs cannot conduct simultaneously. The load voltage is the same as the source voltage when either SCR is on. The load voltage is zero when both SCRs are OFF. The switch voltage vsw is zero when either SCR is ON and is equal to the source voltage when neither is ON. The average current in the source and load is zero if the SCRs are on for equal time intervals. The average current in each SCR is not zero because of unidirectional SCR current. The rms current in each SCR is 1/√2 times the rms load current if the SCRs are on for equal time intervals.
  • 6.
    6 Dr. Firas ObeidatFaculty of Engineering Philadelphia University vs + -vsw S1 S2 + - + - io voR The Single Phase AC Voltage Controller - Resistive Load 𝑣𝑠 𝜔𝑡 = 𝑉𝑚 𝑠𝑖𝑛𝜔𝑡 𝑣𝑠 𝜔𝑡 = 𝑉𝑚 𝑠𝑖𝑛𝜔𝑡 𝛼 < 𝜔𝑡 < 𝜋 𝑎𝑛𝑑 𝜋 + 𝛼 < 𝜔𝑡 < 2𝜋 0 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒 Let the voltage source be Output voltage is The rms load voltage is 𝑉𝑜,𝑟𝑚𝑠 = 1 𝜋 (𝑉𝑚 𝑠𝑖𝑛𝜔𝑡)2 𝑑𝜔𝑡 𝜋 α = 𝑉𝑚 2 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋
  • 7.
    7 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - Resistive Load The power factor of the load is The rms current in the load and the source is 𝐼 𝑜,𝑟𝑚𝑠 = 𝑉𝑜,𝑟𝑚𝑠 𝑅 = 𝑉𝑚 𝑅 2 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 𝑝𝑓 = 𝑃 𝑆 = 𝑉𝑜,𝑟𝑚𝑠 2 𝑅 𝑉𝑠,𝑟𝑚𝑠 𝐼𝑠,𝑟𝑚𝑠 = 𝑉𝑜,𝑟𝑚𝑠 2 𝑅 𝑉𝑠,𝑟𝑚𝑠(𝑉𝑜,𝑟𝑚𝑠 𝑅) = 𝑉𝑜,𝑟𝑚𝑠 𝑉𝑠,𝑟𝑚𝑠 = 𝑉𝑚 2 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 𝑉𝑚 2 𝑝𝑓 = 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 The pf=1 for α=0, which is the same as for an uncontrolled resistive load, and the power factor for α>0 is less than 1. The average source current is zero because of half-wave symmetry. 𝐼𝑠,𝐴𝑣𝑔 = 𝐼 𝑜,𝐴𝑣𝑔 = 0
  • 8.
    8 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - Resistive Load The average SCR current is 𝐼𝑆𝐶𝑅,𝐴𝑣𝑔 = 1 2𝜋 𝑉𝑚 𝑠𝑖𝑛𝜔𝑡 𝑅 𝑑𝜔𝑡 𝜋 𝛼 = 𝑉𝑚 2𝜋𝑅 (1 + 𝑐𝑜𝑠𝛼) 𝐼𝑆𝐶𝑅,𝑟𝑚𝑠 = 1 2𝜋 ( 𝑉𝑚 𝑠𝑖𝑛𝜔𝑡 𝑅 )2 𝑑𝜔𝑡 𝜋 α = 𝑉𝑚 2𝑅 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 The rms SCR current is 𝐼𝑆𝐶𝑅,𝑟𝑚𝑠 = 𝑉𝑚 2 2𝑅 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 = 𝐼 𝑜,𝑟𝑚𝑠 2 πα 2π 2π+α 3π ωt iS1 vs/R
  • 9.
    9 Dr. Firas ObeidatFaculty of Engineering Philadelphia University Example: The single-phase ac voltage controller has a 120-V rms 60-Hz source. The load resistance is 15 Ω. Determine (a) the delay angle required to deliver 500 W to the load, (b) the rms source current, (c) the rms and average currents in the SCRs, (d) the power factor. 𝑉𝑜,𝑟𝑚𝑠 = 𝑉𝑚 2 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 = 2 × 120 2 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 𝑃 = 𝑉𝑜,𝑟𝑚𝑠 2 𝑅 → 𝑉𝑜,𝑟𝑚𝑠 2 = 𝑃𝑅 = 500 × 15 = 7500 𝑉𝑜,𝑟𝑚𝑠 2 = 1202 (1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 ) ∴ 7500 = 14400(1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 ) 𝛼 𝜋 − 𝑠𝑖𝑛2𝛼 2𝜋 = 0.479 2𝛼 − 𝑠𝑖𝑛2𝛼 = 3.01 𝛼 = 1.54 rad = 88.1 𝑜 (a) The Single Phase AC Voltage Controller - Resistive Load
  • 10.
    10 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - Resistive Load (b) 𝐼 𝑜,𝑟𝑚𝑠 = 𝑉𝑜,𝑟𝑚𝑠 𝑅 = 86.6 15 = 5.77 A 𝑉𝑜,𝑟𝑚𝑠 2 = 7500 → 𝑉𝑜,𝑟𝑚𝑠 = 86.6From (a) 𝐼𝑆𝐶𝑅,𝐴𝑣𝑔 = 𝑉𝑚 2𝜋𝑅 1 + 𝑐𝑜𝑠𝛼 = 2 × 120 2𝜋15 1 + 𝑐𝑜𝑠88.1 = 1.86 A 𝐼𝑆𝐶𝑅,𝑟𝑚𝑠 = 𝐼 𝑜,𝑟𝑚𝑠 2 = 5.77 2 = 4.08 A (c) 𝑝𝑓 = 𝑃 𝑆 = 𝑃 𝑉𝑠,𝑟𝑚𝑠 𝐼𝑠,𝑟𝑚𝑠 = 1 − 𝛼 𝜋 + 𝑠𝑖𝑛2𝛼 2𝜋 = 500 120 × 5.77 = 0.722(d)
  • 11.
    11 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - RL Load vs + -vsw S1 S2 + - + - io vo R L When a gate signal is applied to S1 at 𝜔t=α in single phase AC voltage controller with RL load, Kirchhoff’s voltage law for the circuit is expressed as. 𝑉𝑚 𝑠𝑖𝑛𝜔𝑡 = 𝑅𝑖 𝑜 𝑡 + 𝐿 𝑑𝑖 𝑜 𝑡 𝑑𝑡 The solution for current in this equation (as obtained in the controlled half wave rectifier section) is 𝑖 𝑜 𝜔𝑡 = 𝑉𝑚 𝑍 sin 𝜔𝑡 − 𝜃 − sin(𝛼 − 𝜃)𝑒(𝛼−𝜔𝑡) 𝜔𝜏 𝛼 ≤ 𝜔𝑡 ≤ 𝛽 0 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒 where 𝑍 = 𝑅2 + (𝜔𝐿)2 𝜃 = 𝑡𝑎𝑛−1 ( 𝜔𝐿 𝑅 ) The extinction angle 𝛽 is the angle at which the current returns to zero, when 𝜔𝑡= 𝛽, 𝑖 𝑜 𝛽 = 𝑉𝑚 𝑍 sin 𝛽 − 𝜃 − sin(𝛼 − 𝜃)𝑒(𝛼−𝛽) 𝜔𝜏 (1) (2)
  • 12.
    12 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - RL Load A gate signal is applied to S2 at 𝜔t=π+α, and the load current is negative but has a form identical to that of the positive half- cycle. The above equation must be solved numerically for 𝛽. The angle (𝛽-α) is called the conduction angle 𝛶. 𝛶 =𝛽-α In the interval between π and 𝛽 when the source voltage is negative and the load current is still positive, S2 cannot be turned on because it is not forward biased. The gate signal to S2 must be delayed at least until the current in S1 reaches zero, at 𝜔t= 𝛽. The delay angle is therefore at least 𝛽- π. α≥𝛽- π
  • 13.
    13 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - RL Load When α=θ, equation (2) becomes sin 𝛽 − 𝜃 = 0 which has a solution 𝛽 − 𝜃 = π Therefore 𝛶 = 𝜋 When α=θ When 𝛶=𝜋, one SCR is always conducting, and the voltage across the load is the same as the voltage of the source. The load voltage and current are sinusoids for this case, and the circuit is analyzed using phasor analysis for AC circuits. The power delivered to the load is continuously controllable between the two extremes corresponding to full source voltage and zero. The expression of rms load current is 𝐼 𝑜,𝑟𝑚𝑠 = 1 𝜋 𝑖 𝑜 2 (𝜔𝑡) 𝑑𝜔𝑡 𝛽 α = 1 𝜋 𝑉 𝑚 𝑍 sin 𝜔𝑡 − 𝜃 − 𝑉 𝑚 𝑍 sin(𝛼 − 𝜃)𝑒(𝛼−𝜔𝑡) 𝜔𝜏 2 𝑑𝜔𝑡 𝛽 α
  • 14.
    14 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - RL Load The average output voltage can be found as An other way to find the expression of rms load current is 𝐼 𝑜,𝑟𝑚𝑠 = 1 𝑅2 + (𝜔𝐿)2 𝑉𝑚 2 1 𝜋 (𝛽 − 𝛼 − 1 2 𝑠𝑖𝑛2𝛽 + 1 2 𝑠𝑖𝑛2𝛼) Power absorbed by the load is determined from 𝑃 = 𝐼 𝑜,𝑟𝑚𝑠 2 𝑅 The power factor of the load is 𝑝𝑓 = 𝑃 𝑆 = 𝑉𝑜,𝑟𝑚𝑠 𝐼 𝑜,𝑟𝑚𝑠 𝑉𝑠,𝑟𝑚𝑠 𝐼𝑠,𝑟𝑚𝑠 = 𝑉𝑜,𝑟𝑚𝑠 𝑉𝑠,𝑟𝑚𝑠 = 1 𝜋 (𝛽 − 𝛼 − 1 2 𝑠𝑖𝑛2𝛽 + 1 2 𝑠𝑖𝑛2𝛼) 𝑉𝑜,𝑟𝑚𝑠 = 1 𝜋 (𝑉𝑚 𝑠𝑖𝑛𝜔𝑡)2 𝑑𝜔𝑡 𝛽 α = 𝑉𝑚 2 1 𝜋 (𝛽 − 𝛼 − 1 2 𝑠𝑖𝑛2𝛽 + 1 2 𝑠𝑖𝑛2𝛼)
  • 15.
    15 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - RL Load Each SCR carries one-half of the current waveform, making the average SCR current 𝐼𝑆𝐶𝑅,𝐴𝑣𝑔 = 1 2𝜋 𝑖 𝑜(𝜔𝑡) 𝑑𝜔𝑡 𝛽 α = 1 2𝜋 𝑉𝑚 𝑍 sin 𝜔𝑡 − 𝜃 − sin(𝛼 − 𝜃)𝑒(𝛼−𝜔𝑡) 𝜔𝜏 𝑑𝜔𝑡 𝛽 α The rms current in each SCR is 𝐼𝑆𝐶𝑅,𝑟𝑚𝑠 = 𝐼 𝑜,𝑟𝑚𝑠 2 The average load current is zero, 𝐼 𝑜,𝐴𝑣𝑔 = 0
  • 16.
    16 Dr. Firas ObeidatFaculty of Engineering Philadelphia University Example: For the single-phase voltage controller with RL load, the source is 120Vrms at 60 Hz, and the load is a series RL combination with R=20Ω and L=50mH. The delay angle α is 90. Determine (a) an expression for load current for the first half-period, (b) the rms load current, (c) the rms SCR current, (d) the average SCR current, (e) the power delivered to the load, and (f) the power factor. (a) The Single Phase AC Voltage Controller - RL Load The extinction angle is determined from the numerical solution of i(β)=0 in the above equation.
  • 17.
    17 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Single Phase AC Voltage Controller - RL Load (b) (c) (d) (e) (f) 𝐼 𝑜,𝑟𝑚𝑠 = 1 27.5 × 120 × 1 𝜋 (3.83 − 1.57 − 1 2 𝑠𝑖𝑛440 + 0) = 3.27 A 𝐼 𝑜,𝑟𝑚𝑠 = 1 𝑅2 + (𝜔𝐿)2 𝑉𝑚 2 1 𝜋 (𝛽 − 𝛼 − 1 2 𝑠𝑖𝑛2𝛽 − 1 2 𝑠𝑖𝑛2𝛼) Or
  • 18.
    18 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load  The power delivered to the load in three phase AC voltage controller with Y-connected resistive load is controlled by the delay angle α on each thyristor. The six thyristors are turned on in the sequence 1-2- 3-4-5-6, at 60 intervals. Gate signals are maintained throughout the possible conduction angle. + - S4 S1 + - S6 S3 + - S2 S5 A B C ab c R RR n N  The instantaneous voltage across each phase of the load is determined by which thyristors are conducting. At any instant, three thyristors , two thyristors , or no thyristors are ON.  The instantaneous load voltages are either a line-to-neutral voltage (three thyristors ON), one-half of a line-to-line voltage (two thyristors ON), or zero (none on).  Which thyristors are conducting depends on the delay angle α and on the source voltages at a particular instant. The ranges of α that produce particular types of load voltages are 0< α<60o, 60o< α<90o and 90o< α<150o.
  • 19.
    19 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o  To study the output voltage Van, Vbn and Vcn, triggering angle α must be determined first.  Suppose that the triggering angle α equal to 30o.  The output voltage Van will be studies when α= 30o, and the same procedure can be applied to get the output voltages Vbn and Vcn at any triggering angle from 0 to 60o. 𝑉𝐴𝑁 = 𝑉𝑚sin𝜔t 𝑉𝐵𝑁 = 𝑉𝑚sin(𝜔t-2π/3) 𝑉𝐶𝑁 = 𝑉𝑚sin(𝜔t-4π/3) Let 𝑉𝐴𝐵 = 3𝑉𝑚sin(𝜔t+π/6) 𝑉𝐵𝐶 = 3𝑉𝑚sin(𝜔t-π/2) 𝑉𝐶𝐴 = 3𝑉𝑚sin(𝜔t-7π/6) VAN VBN VCN 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o
  • 20.
    20 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o 1. Determine the triggering angle α (for example α= 30o). 2. Determine the conducting period for each thyristor. • As seen from the input phase voltages VAN, VBN and VCN, every 30o there is a change that affect on the conduction of each thyristor. VAN VBN VCN 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o VAN=VCN VCN=0 VBN=0 VAN=VBN VAN=0 VCN=0 VBN=VCN VBN=0 VAN=0 VAN=VBNVAN=VCNVBN=VCN
  • 21.
    21 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o VAN VBN VCN iG1 iG6 iG5 iG4 iG3 iG2 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o • Because α=30o, S1 will be triggered at 30o, S3 will be triggered at 150o (120o+α), S5 will be triggered at 270o (240o+α). • S4 will be triggered after S1 by 180o, S6 will be triggered after S3 by 180o S2 will be triggered after S5 by 180o. • The six SCRs are turned on in the sequence 1-2-3-4-5-6, at 60o intervals. + - S4 S1 + - S6 S3 + - S2 S5 A B C ab c R RR n N
  • 22.
    22 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o 3. Study the conduction period for each thyristor. • Each thyristor will be studied at each angle that affect on the conduction of each thyristor to determine if the thyristor will conduct or not. • The conduction period will be studied for S1. • At 30o, VAN=VCN, VAN and VCN are positive, while VBN is negative. So, the current will flow from phase A and C to phase B. S1 will be on from 30o to 60o. VAN VBN VCN iG1 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o + - S4 S1 + - S6 S3 + - S2 S5 A B C a b c R RR n N + + -
  • 23.
    23 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o • At 60o, VCN=0, VAN is positive, while VBN is negative. So, the current will flow from phase Ato phase B. S1 will be ON from 60o to 90o. VAN VBN VCN iG1 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o + - S4 S1 + - S6 S3 + - S2 S5 A B C a b c R RR n N + 0 -
  • 24.
    24 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o • At 90o, VBN=VCN, VAN is positive, while VBN and VCN are negative. So, the current will flow from phase Ato phase B and phase C. S1 will be ON from 90o to 120o. + - S4 + - S6 S3 + - S2 S5 A B C a b c R RR n N + - - VAN VBN VCN iG1 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o
  • 25.
    25 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o • At 120o, VBN=0, VAN is positive, while VCN is negative. So, the current will flow from phase Ato phase C. S1 will be ON from 120o to 150o. + - S4 S1 + - S6 S3 + - S2 S5 A B C a b c R RR n N + 0 - VAN VBN VCN iG1 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o
  • 26.
    26 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o • At 150o, VAN=VBN, VAN and VBN are positive, VCN is negative. So, the current will flow from phase A and B to phase C. S1 will be ON from 150o to 180o. + - S4 S1 + - S6 S3 + - S2 S5 A B C a b c R RR n N + + - VAN VBN VCN iG1 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o
  • 27.
    27 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o • At 180o, VAN=0, VBN is positive, VCN is negative. So, the current will flow from phase B to phase C and the current will not flow in phase A. S1 will be OFF from 180o to 210o. • At 210o, VAN= VCN, VBN is positive, VAN and VCN are negative. So, the current will flow from phase B to phase A and C. S1 will be OFF from 210o to 240o. • At 240o, VCN= 0, VBN is positive, VAN is negative. So, the current will flow from phase B to phase A. S1 will be OFF from 240o to 270o. • At 270o, VBN=VCN, VBN and VCN are positive, VAN is negative. So, the current will flow from phase B and C to phase A. S1 will be OFF from 270o to 300o. • At 300o, VBN=0, VCN is positive, VAN is negative. So, the current will flow from phase C to phase A. S1 will be OFF from 300o to 330o. • At 330o, VAN=VBN, VCN is positive, VAN and VBN are negative. So, the current will flow from phase C to phase A and B. S1 will be OFF from 330o to 360o.
  • 28.
    28 Dr. Firas ObeidatFaculty of Engineering Philadelphia University • The same procedure can be done for other thyristors to determine the conduction period for each thyristor. 4. Determine the thyristors that will be conducted for each period. For example, when 0<ωt<30o, S5 and S6 will be conducted, when 30o<ωt<60o, S5, S6 and S1 will be conducted, ect… VAN VBN VCN iG1 iG6 iG5 iG4 iG3 iG2 6,1,2 2,3,41,2,36,1 2,31,2 3,4 3,4,5 4,5 4,5,65,6 5,6,1 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o
  • 29.
    29 Dr. Firas ObeidatFaculty of Engineering Philadelphia University 5. Determine the output voltages (Van, Vbn and Vcn) at each period. • The output voltage Van can be found by applying the thyristors that will be conducted at each period. • when 0<ωt<30o, S5 and S6 will be conducted which means that the current will flow from phase C to phase B, and there is no current will flow in phase A. In this period Van=0. • when 30o<ωt<60o, S5, S6 and S1 will be conducted which means that the current will flow from phase A and C to phase B. In this period Van=VAN. The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o + - S4 S1 + - S6 S3 + - S2 S5 A B C a b c R RR n N 0 + - + - S4 S1 + - S6 S3 + - S2 S5 A B C a b c R RR n N + + - 0<ωt<30o 30o<ωt<60o
  • 30.
    30 Dr. Firas ObeidatFaculty of Engineering Philadelphia University • when 60o<ωt<90o, S6 and S1 will be conducted which means that the current will flow from phase A to phase B, and there is no current will flow in phase C. In this period Van=VAB/2. • After completing the output voltage Van for the whole period, the waveform of Van can be found from the waveforms VAN, VAB/2, VAC/2 and zero. The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o + - S4 S1 + - S6 S3 + - S2 S5 A B C a b c R RR n N + 0 - 60o<ωt<90o VAN VBN VCN iG1 iG6 iG5 iG4 iG3 iG2 6,1,2 2,3,41,2,36,1 2,31,2 3,4 3,4,5 4,5 4,5,65,6 5,6,1 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o 0 VAN VAB/2 VAN VAC/2 VAN 0 VAN VAB/2 VAN VAC/2 VANVan
  • 31.
    31 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o VAN VBN VCN iG1 iG6 iG5 iG4 iG3 iG2 6,1,2 2,3,41,2,36,1 2,31,2 3,4 3,4,5 4,5 4,5,65,6 5,6,1 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o 0 VAN VAB/2 VAN VAC/2 VAN 0 VAN VAB/2 VAN VAC/2 VANVan VAB/2 VAN VAC/2 Van  The figure below shows the final shape for the output voltage Van. The rms voltage for this waveform will be less than the rms voltage for the input voltages VAN, VBN and VCN. 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o Van 360o
  • 32.
    32 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 0 ≤ α<60o  The other output waveforms (Vbn and Vcn) can be found by the same way, and the resulting waveform of Vbn will be the same as the waveform of Van shifted by 120o, and the waveform of Vbn will be the same as the waveform of Van shifted by 240o.  At any instant, three thyristors or two thyristors are ON. The instantaneous load voltages are either a line-to-neutral voltage (three thyristors ON), one-half of a line-to-line voltage (two thyristors ON), or zero (none ON)  Because the load is resistive load, the shape of the output current is similar to the shape of the output voltage.
  • 33.
    33 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 60o ≤ α<90o  Only two thyristors conduct at any one time when the delay angle is between 60o and 90o.  For α=75o , prior to 75o, S5 and S6 are conducting, and Van=0. When S1 is turned on at 75o, S6 continues to conduct, but S5 must turn off because VCN is negative. Voltage Van is then VAB/2. When S2 is turned on at 135 , S6 is forced off, and Van= VAC/2. The next thyristor to turn on is S3, which forces S1 off, and Van=0. One thyristor is always forced off when thyristor is turned on for α in this range. Load voltages are one-half line-to-line voltages or zero.
  • 34.
    34 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load When 90o ≤ α<150o  Only two thyristors conduct at any one time when the delay angle is between 90o and 150o.  For α=120o , prior to 120o, no thyristors are on, and Van=0. At α=120o, S1 is turned on at 120o, S6 still has a gate signal applied. Since VAB is positive, both S1 and S6 are forward- biased and begin to conduct, and Van=VAB/2. Both S1 and S6 turn off when VAB becomes negative. When a gate signal is applied to S2, it turns on, and S1 turns on again. For α>150o, there is no time interval when thyristor is forward-biased while a gate signal is applied. Output voltage is zero for this condition.
  • 35.
    35 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load The rms output voltage for a Y– connection loads are found to be:  For 0o≤ α<60o 𝑽 𝒐,𝒓𝒎𝒔 = 𝟑𝑽 𝒎 𝟏 𝝅 𝝅 𝟔 − 𝜶 𝟒 + 𝒔𝒊𝒏𝟐𝜶 𝟖 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝟐𝝅 𝑽 𝒂𝒏 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟎 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝝅 𝑽 𝑨𝑵 𝟐 𝒅𝝎𝒕 𝝅 𝟑 𝜶 + ( 𝑽 𝑨𝑩 𝟐 ) 𝟐 𝒅𝝎𝒕 𝝅 𝟑+𝜶 𝝅 𝟑 + 𝑽 𝑨𝑵 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟑 𝝅 𝟑+𝜶 + ( 𝑽 𝑨𝑪 𝟐 ) 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟑+𝜶 𝟐𝝅 𝟑 + 𝑽 𝑨𝑵 𝟐 𝒅𝝎𝒕 𝝅 𝟐𝝅 𝟑+𝜶 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝝅 (𝑽 𝒎sin𝜔t ) 𝟐 𝒅𝝎𝒕 𝝅 𝟑 𝜶 + ( 𝟑𝑽 𝒎sin(𝜔t+π/6) 𝟐 ) 𝟐 𝒅𝝎𝒕 𝝅 𝟑+𝜶 𝝅 𝟑 + (𝑽 𝒎sin𝜔t ) 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟑 𝝅 𝟑+𝜶 + ( 𝟑𝑽 𝒎sin(𝜔t−π/6) 𝟐 ) 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟑+𝜶 𝟐𝝅 𝟑 + (𝑽 𝒎sin𝜔t ) 𝟐 𝒅𝝎𝒕 𝝅 𝟐𝝅 𝟑+𝜶
  • 36.
    36 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load The rms output voltage for a Y– connection loads are found to be:  For 60o≤ α<90o 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝟐𝝅 𝑽 𝒂𝒏 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟎 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝝅 ( 𝑽 𝑨𝑩 𝟐 ) 𝟐 𝒅𝝎𝒕 𝝅 𝟑+𝜶 𝜶 + ( 𝑽 𝑨𝑪 𝟐 ) 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟑+𝜶 𝟐𝝅 𝟑 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝝅 ( 𝟑𝑽 𝒎sin(𝜔t+π/6) 𝟐 ) 𝟐 𝒅𝝎𝒕 𝝅 𝟑+𝜶 𝜶 + ( 𝟑𝑽 𝒎sin(𝜔t−π/6) 𝟐 ) 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟑+𝜶 𝟐𝝅 𝟑 𝑉𝑜,𝑟𝑚𝑠 = 3𝑉𝑚 1 𝜋 𝜋 12 + 3𝑠𝑖𝑛2𝛼 16 + 3𝑐𝑜𝑠2𝛼 16
  • 37.
    37 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load The rms output voltage for a Y– connection loads are found to be:  For 90o≤ α<150o 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝟐𝝅 𝑽 𝒂𝒏 𝟐 𝒅𝝎𝒕 𝟐𝝅 𝟎 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝝅 ( 𝑽 𝑨𝑩 𝟐 ) 𝟐 𝒅𝝎𝒕 𝟓𝝅 𝟔 𝜶 + ( 𝑽 𝑨𝑪 𝟐 ) 𝟐 𝒅𝝎𝒕 𝟕𝝅 𝟔 𝝅 𝟑+𝜶 𝑽 𝒐,𝒓𝒎𝒔 = 𝟏 𝝅 ( 𝟑𝑽 𝒎sin(𝜔t+π/6) 𝟐 ) 𝟐 𝒅𝝎𝒕 𝟓𝝅 𝟔 𝜶 + ( 𝟑𝑽 𝒎sin(𝜔t−π/6) 𝟐 ) 𝟐 𝒅𝝎𝒕 𝟕𝝅 𝟔 𝝅 𝟑+𝜶 𝑽 𝒐,𝒓𝒎𝒔 = 𝟑𝑽 𝒎 𝟏 𝝅 𝟓𝝅 𝟐𝟒 − 𝜶 𝟒 + 𝒔𝒊𝒏𝟐𝜶 𝟏𝟔 − 𝟑𝒄𝒐𝒔𝟐𝜶 𝟏𝟔
  • 38.
    38 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Y Connected Resistive Load Example: a three phase bidirectional AC voltage controller Y-connected connected to resistive load (R=10Ω). The supply voltage VL-L=208V, f=60Hz. If α=π/6, find the output voltage rms value and the input power factor. 𝑉𝑜,𝑟𝑚𝑠 = 3𝑉𝑚 1 𝜋 𝜋 6 − 𝛼 4 + 𝑠𝑖𝑛2𝛼 8 = 208 1 𝜋 𝜋 6 − π/6 4 + 𝑠𝑖𝑛2π/6 8 = 83𝑉 𝐼 𝑜,𝑟𝑚𝑠 = 𝑉𝑜,𝑟𝑚𝑠 𝑅 = 83 10 = 8.3𝐴 𝑃𝑜,𝑎𝑐 = 3𝐼 𝑜,𝑟𝑚𝑠 2 𝑅 = 3 × 8.32 × 10 = 2066.7𝑊 𝑆 = 3𝐼 𝑜,𝑟𝑚𝑠 𝑉𝑖𝑛𝑝𝑢𝑡,𝑟𝑚𝑠 = 3 × 8.3 × 84.9 = 2114.4𝑉𝐴 𝑉𝑖𝑛𝑝𝑢𝑡,𝑟𝑚𝑠 = 208 2 3 = 84.9𝑉 𝑝𝑓 = 𝑃𝑜,𝑎𝑐 𝑆 = 2066.7 2114.4 = 0.977
  • 39.
    39 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Δ Connected Resistive Load  The voltage across a load resistor is the corresponding line-to-line voltage when a thyristor in the phase is on. The delay angle is referenced to the zero crossing of the line-to-line voltage. thyristors are turned on in the sequence 1-2-3-4-5-6. The line current in each phase is the sum of two of the delta currents:
  • 40.
    40 Dr. Firas ObeidatFaculty of Engineering Philadelphia University The Three Phase AC Voltage Controller – Δ Connected Resistive Load The relationship between rms line and delta currents depends on the conduction angle of the thyristors. For small conduction angles (large α), the delta currents do not overlap, and the rms line currents are Current waveforms for α=130o For large conduction angles (small α), the delta currents overlap, and the rms line current is larger than √2IΔ. In the limit when γ (α=0), the delta currents and line currents are sinusoids. The rms line current is determined from ordinary three- phase analysis. Current waveforms for α=90o The range of rms line current is therefore depending on α
  • 41.