Discrete Models in Computer Vision

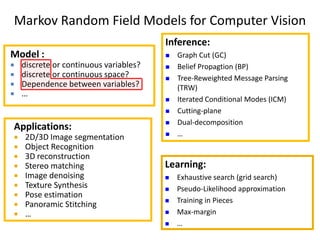
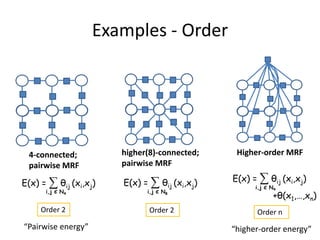
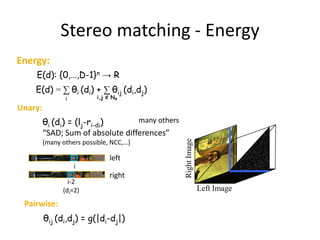
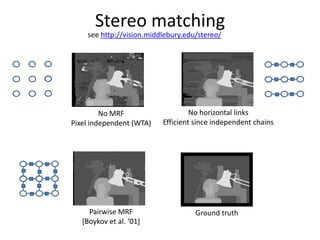
Course Program
9.30-10.00 Introduction (Andrew Blake)
10.00-11.00 Discrete Models in Computer Vision (Carsten Rother)
15min Coffee break
11.15-12.30 Message Passing: DP, TRW, LP relaxation (Pawan Kumar)
12.30-13.00 Quadratic pseudo-boolean optimization (Pushmeet Kohli)
1 hour Lunch break
14:00-15.00 Transformation and move-making methods (Pushmeet Kohli)
15:00-15.30 Speed and Efficiency (Pushmeet Kohli)
15min Coffee break
15:45-16.15 Comparison of Methods (Carsten Rother)
16:15-17.30 Recent Advances: Dual-decomposition, higher-order, etc.
(Carsten Rother + Pawan Kumar)

All online material will be online (after conference):
http://research.microsoft.com/en-us/um/cambridge/projects/tutorial/

Discrete Models in Computer Vision

Carsten Rother
Microsoft Research Cambridge

Overview

• Introduce Factor graphs notation
• Categorization of models in Computer Vision:
– 4-connected MRFs
– Highly-connected MRFs
– Higher-order MRFs

Markov Random Field Models for Computer Vision
Inference:
Model :  Graph Cut (GC)
 discrete or continuous variables?  Belief Propagtion (BP)
 discrete or continuous space?  Tree-Reweighted Message Parsing
 Dependence between variables? (TRW)
 …
 Iterated Conditional Modes (ICM)
 Cutting-plane
 Dual-decomposition
Applications:
 2D/3D Image segmentation  …
 Object Recognition
 3D reconstruction
 Stereo matching Learning:
 Image denoising  Exhaustive search (grid search)
 Texture Synthesis  Pseudo-Likelihood approximation
 Pose estimation
 Training in Pieces
 Panoramic Stitching
 …  Max-margin
 …

Recap: Image Segmentation

Input z Maximum-a-posteriori (MAP)
x* = argmax P(x|z) = argmin E(x)
x x

P(x|z) ~ P(z|x) P(x) Posterior; Likelihood; Prior

P(x|z) ~ exp{-E(x)} Gibbs distribution

E: {0,1}n → R
E(x) = ∑ θi (xi) + w∑ θij (xi,xj) Energy
i i,j Є N4
Unary term Pairwise term

Min-Marginals
(uncertainty of MAP-solution)

Definition: ψv;i = min E(x)
xv=i

image MAP Min-Marginals
(foreground)
(bright=very certain)
Can be used in several ways:
• Insights on the model
• For optimization (TRW, comes later)

Introducing Factor Graphs
Write probability distributions as Graphical models:

- Direct graphical model
- Undirected graphical model (… what Andrew Blake used)
- Factor graphs

References:
- Pattern Recognition and Machine Learning *Bishop ‘08, book, chapter 8+
- several lectures at the Machine Learning Summer School 2009
(see video lectures)

Factor Graphs
P(x) ~ θ(x1,x2,x4) θ(x3,x4) θ(x2,x3) θ(x4,x5) “4 factors”

P(x) ~ exp{-E(x)} Gibbs distribution
E(x) = θ(x1,x2,x3) + θ(x2,x4) + θ(x3,x4) + θ(x3,x5)

unobserved/latent/hidden variable
x1 x2
variables are in same factor.

x3 x4

x5

Factor graph

Definition “Order”
Definition “Order”:
The arity (number of variables) of
the largest factor x1 x2

P(X) ~ θ(x1,x2,x3) θ(x2,x4) θ(x3,x4) θ(x3,x5)

arity 3 arity 2 x3 x4

x5

Factor graph
with order 3

Examples - Order

4-connected; higher(8)-connected; Higher-order MRF
pairwise MRF pairwise MRF

E(x) = ∑ θij (xi,xj) E(x) = ∑ θij (xi,xj) E(x) = ∑ θij (xi,xj)
i,j Є N4
i,j Є N4 i,j Є N8
+θ(x1,…,xn)
Order 2 Order 2 Order n
“Pairwise energy” “higher-order energy”

Example: Image segmentation
P(x|z) ~ exp{-E(x)}
E(x) = ∑ θi (xi,zi) + ∑ θij (xi,xj)
i i,j Є N4

Observed variable

Unobserved (latent) variable
zi

xj xi

Factor graph

Most simple inference technique:
ICM (iterated conditional mode)
Goal: x* = argmin E(x)
x2 x
E(x) = θ12 (x1,x2)+ θ13 (x1,x3)+
θ14 (x1,x4)+ θ15 (x1,x5)+…

x3 x1 x4

x5

Most simple inference technique:
ICM (iterated conditional mode)
means observed
Goal: x* = argmin E(x)
x2 x
E(x) = θ12 (x1,x2)+ θ13 (x1,x3)+
θ14 (x1,x4)+ θ15 (x1,x5)+…

x3 x1 x4

x5

Simulated Annealing: accept a move even if ICM Global min
energy increases (with certain probability) Can get stuck in local minima!

Overview
• Categorization of models in Computer Vision:




Stereo matching
d=0

d=4

Image – left(a) Image – right(b) Ground truth depth

• Images rectified
• Ignore occlusion for now

Energy: di

E(d): {0,…,D-1}n → R
Labels: d (depth/shift)

Stereo matching - Energy
Energy:
E(d): {0,…,D-1}n → R
E(d) = ∑ θi (di) + ∑ θij (di,dj)
i i,j Є N4

Unary:
θi (di) = (lj-ri-di) many others
“SAD; Sum of absolute differences”

Right Image
(many others possible, NCC,…)

left
i
right
i-2
(di=2) Left Image
Pairwise:
θij (di,dj) = g(|di-dj|)

Stereo matching - prior


cost
|di-dj|

No truncation
(global min.)

[Olga Veksler PhD thesis,
Daniel Cremers et al.]



cost
|di-dj|
discontinuity preserving potentials
*Blake&Zisserman’83,’87+

No truncation with truncation
(global min.) (NP hard optimization)

[Olga Veksler PhD thesis,
Daniel Cremers et al.]

Stereo matching
see http://vision.middlebury.edu/stereo/

No MRF No horizontal links
Pixel independent (WTA) Efficient since independent chains

Pairwise MRF Ground truth
[Boykov et al. ‘01+

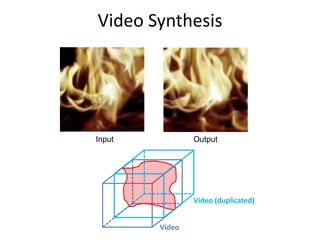
Texture synthesis

Input

Output

Good case: Bad case:
b b b
a a
i j i j
a

E: {0,1}n → R
O E(x) = ∑ |xi-xj| [ |ai-bi|+|aj-bj| ]
i,j Є N4
1
[Kwatra et. al. Siggraph ‘03 +

Video Synthesis

Input Output

Video (duplicated)

Video

AutoCollage

http://research.microsoft.com/en-us/um/cambridge/projects/autocollage/ [Rother et. al. Siggraph ‘05 +

Recap: 4-connected MRFs

• A lot of useful vision systems are based on
4-connected pairwise MRFs.

• Possible Reason (see Inference part):
a lot of fast and good (globally optimal)
inference methods exist

Overview
• Categorization of models in Computer Vision?




Why larger connectivity?
We have seen…
• “Knock-on” effect (each pixel influences each other pixel)
• Many good systems

What is missing:
1. Modelling real-world texture (images)
2. Reduce discretization artefacts
3. Encode complex prior knowledge
4. Use non-local parameters

Reason 1: Texture modelling

Training images Test image Test image (60% Noise)

Result MRF Result MRF Result MRF
4-connected 4-connected 9-connected
(neighbours) (7 attractive; 2 repulsive)

Reason1: Texture Modelling
input output

[Zalesny et al. ‘01+

Reason2: Discretization artefacts

1
Length of the paths:

Eucl. 4-con. 8-con.
5.65 6.28 5.08
8 6.28 6.75

Larger connectivity can model true Euclidean
length (also other metric possible)

*Boykov et al ‘03, ‘05+


4-connected 8-connected 8-connected
Euclidean Euclidean geodesic

higher-connectivity can model
true Euclidean length [Boykov et al. ‘03; ‘05+

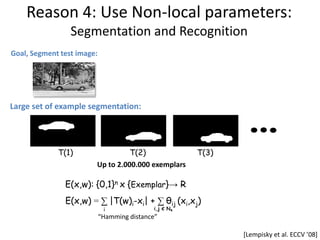
3D reconstruction

[Slide credits: Daniel Cremers]

Reason 3: Encode complex prior knowledge:
Stereo with occlusion

E(d): {1,…,D}2n → R
Each pixel is connected to D pixels in the other image
d=1 (∞ cost)
1 1

d=10 (match)
θlr (dl,dr) = d d
match
d=20 (0 cost)

D D
dl dr Left view right view

Stereo with occlusion

Ground truth Stereo with occlusion Stereo without occlusion
[Kolmogrov et al. ‘02+ *Boykov et al. ‘01+

Reason 4: Use Non-local parameters:
Interactive Segmentation (GrabCut)

[Boykov and Jolly ’01+

GrabCut *Rother et al. ’04+

Interactive Segmentation (GrabCut)

w
Model jointly segmentation and color model:

E(x,w): {0,1}n x {GMMs}→ R
E(x,w) = ∑ θi (xi,w) + ∑ θij (xi,xj)
i i,j Є N4

An object is a compact set of colors:
Red
Red

[Rother et al Siggraph ’04+

Segmentation and Recognition
Goal, Segment test image:

1

Large set of example segmentation:

T(1) T(2) T(3)
Up to 2.000.000 exemplars

E(x,w): {0,1}n x {Exemplar}→ R
E(x,w) = ∑ |T(w)i-xi| + ∑ θij (xi,xj)
i i,j Є N4
“Hamming distance”

[Lempisky et al. ECCV ’08+

Segmentation and Recognition

UIUC dataset; 98.8% accuracy

[Lempisky et al. ECCV ’08+

Why Higher-order Functions?
In general θ(x1,x2,x3) ≠ θ(x1,x2) + θ(x1,x3) + θ(x2,x3)

Reasons for higher-order MRFs:

1. Even better image(texture) models:
– Field-of Expert [FoE, Roth et al. ‘05+
– Curvature *Woodford et al. ‘08+

2. Use global Priors:
– Connectivity *Vicente et al. ‘08, Nowizin et al. ‘09+
– Encode better training statistics *Woodford et al. ‘09+

Reason1: Better Texture Modelling

Higher Order Structure
not Preserved

Training images

Test Image Test Image (60% Noise) Result pairwise MRF Higher-order MRF
9-connected
*Rother et al CVPR ‘09+

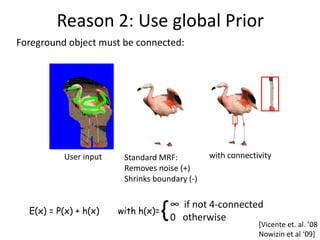
Reason 2: Use global Prior
Foreground object must be connected:

User input Standard MRF: with connectivity
Removes noise (+)
Shrinks boundary (-)

E(x) = P(x) + h(x) with h(x)= {
∞ if not 4-connected
0 otherwise
[Vicente et. al. ’08
Nowizin et al ‘09+

Reason 2: Use global Prior
What is the prior of a MAP-MRF solution:

Training image: 60% black, 40% white

MAP: Others less likely :
8
prior(x) = 0.6 = 0.016 prior(x) = 0.6 5 * 0.4 3 = 0.005
MRF is a bad prior since input marginal statistic ignored !

Introduce a global term, which controls global stats:

Noisy input

Ground truth Pairwise MRF – Global gradient prior
Increase Prior strength
[Woodford et. al. ICCV ‘09]
(see poster on Friday)

Summary
• Categorization of models in Computer Vision?




…. all useful models,
but how do I optimize them?

Markov Property

xi

• Markov Property: Each variable is only connected to a few others,
i.e. many pixels are conditional independent
• This makes inference easier (possible at all)
• But still… every pixel can influence any other pixel (knock-on effect)

Recap: Factor Graphs

• Factor graphs: very good representation since it
reflects directly the given energy

• MRF (Markov Property) means many pixels are
conditional independent

• Still … all pixels influence each other (knock-on effect)

Interactive Segmentation - Tutorial example

Goal

z = (R,G,B)n x = {0,1}n

Given Z and unknown (latent) variables x:

P(x|z) = P(z|x) P(x) / P(z) ~ P(z|x) P(x)
Posterior Likelihood Prior
Probability (data- (data-
dependent) independent)

Maximium a Posteriori (MAP): x* = argmax P(x|z)
X

Likelihood P(x|z) ~ P(z|x) P(x)

Green
Green

Red Red

Prior P(x|z) ~ P(z|x) P(x)

xi xj

P(x) = 1/f ∏ θij (xi,xj)
i,j Є N

f = ∑ ∏ θij (xi,xj) “partition function”
x i,j Є N

θij (xi,xj) = exp{-|xi-xj|} “ising prior”

(exp{-1}=0.36; exp{0}=1)

Posterior distribution
P(x|z) ~ P(z|x) P(x)

Posterior “Gibbs” distribution:

θi (xi,zi) = P(zi|xi=1) xi + P(zi|xi=0) (1-xi) Likelihood
θ (x ,x ) = |x -x | prior
ij i j i j

P(x|z) = 1/f(z,w) exp{-E(x,z,w)}
f(z,w) = ∑ exp{-E(x,z,w)}
X
E(x,z,w) = ∑ θi (xi,zi) + w∑ θij (xi,xj) Energy
i i,j
Unary terms Pairwise terms
Note, likelihood can be an arbitrary function of the data

Energy minization
P(x|z) = 1/f(z,w) exp{-E(x,z,w)}
-log P(x|z) = -log (1/f(z,w)) + E(x,z,w)
f(z,w) = ∑ exp{-E(x,z,w)}
X

x* = argmin E(x,z,w)
X
MAP same as minimum Energy

MAP; Global min E ML

Weight prior and likelihood

w =0 w =10

w =40 w =200

E(x,z,w) = ∑ θi (xi,zi) + w∑ θij (xi,xj)

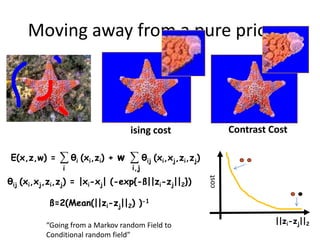
Moving away from a pure prior …

ising cost Contrast Cost

E(x,z,w) = ∑ θi (xi,zi) + w ∑ θij (xi,xj,zi,zj)
i i,j

θij (xi,xj,zi,zj) = |xi-xj| (-exp{-ß||zi-zj||2})

cost
ß=2(Mean(||zi-zj||2) )-1

“Going from a Markov random Field to ||zi-zj||2
Conditional random field”

Tree vs Loopy graphs
Markov blanket of xi:
all variables which are
in same factor as xi [Felzenschwalb, Huttenlocher ‘01+

xi root

- MAP (in general) NP hard tree chain
(see inference part)
- Marginals P(xi) also NP hard • MAP is tractable
• Marginal, e.g. P(foot), tractable


cost
Left image
|di-dj|

Potts model

(Potts model) Smooth disparities

[Olga Veksler PhD thesis]

Modelling texture [Zalesny et al ‘01+
“Unary only”

“8 connected
MRF”

input
“13 connected
MRF”

θij (xi,xj) = ∆a / (2*dis(xi,xj)) |xi –xj| √2 ∆a = π/4

1 1

Length of the path
4-con. 8-con. true euc.
6.28 5.08 5.65
6.28 6.75 8

Larger connectivity can model true Euclidean length
(also any Riemannian metric, e.g. geodesic length, can be
modelled)
*Boykov et al ‘03, ‘05+

References Higher-order Functions?
• In general θ(x1,x2,x3) ≠ θ(x1,x2) + θ(x1,x3) + θ(x2,x3)

Field of Experts Model (2x2; 5x5)
*Roth, Black CVPR ‘05 +
[Potetz, CVPR ‘07+

Minimize Curvature (3x1)
*Woodford et al. CVPR ‘08 +

Large Neighbourhood (10x10 -> whole image)
*Rother, Kolmogorov, Minka & Blake, CVPR ‘06+
*Vicente, Kolmogorov, Rother, CVPR ‘08+
[Komodiakis, Paragios, CVPR ‘09+
*Rother, Kohli, Feng, Jia, CVPR ‘09+
*Woodford, Rother, Kolmogorov, ICCV ‘09+
*Vicente, Kolmogorov, Rother, ICCV ‘09+
*Ishikawa, CVPR ‘09+
*Ishikawa, ICCV ‘09+

Conditional Random Field (CRF)
E(x) = ∑ θi (xi,zi) + ∑ θij (xi,xj,zi,zj) θij
i i,j Є N4

with θij (xi,xj,zi,zj) = |xi-xj| exp(-ß||zi-zj||2)

||zi-zj||2

zjj

zii
z

xjj

xji Ising cost Contrast Cost

Factor graph
Definition CRF: all factors may depend on the data z
No problem for inference (but parameter learning)

Discrete Models in Computer Vision

More Related Content

What's hot

Similar to Discrete Models in Computer Vision

Discrete Models in Computer Vision