This document summarizes a seminar on kernels and support vector machines. It begins by explaining why kernels are useful for increasing flexibility and speed compared to direct inner product calculations. It then covers definitions of positive definite kernels and how to prove a function is a kernel. Several kernel families are discussed, including translation invariant, polynomial, and non-Mercer kernels. Finally, the document derives the primal and dual problems for support vector machines and explains how the kernel trick allows non-linear classification.

1. Seminar 2
Kernels
and
Support Vector Machines
Edgar Marca
Supervisor: DSc. André M.S. Barreto
Petrópolis, Rio de Janeiro - Brazil
September 2nd, 2015
1 / 28

2. Kernels

3. Kernels
Why Kernalize?
At first sight, introducing k(x, x′) has not improved our situation.
Instead of calculating ⟨Φ(xi), Φ(xj)⟩ for i, j = 1, . . . n we have to
calculate k(xi, xj), which has exactly the same values. However, there
are two potential reasons why the kernelized setup can be
advantageous:
▶ Speed: We might find and expression for k(xi, xj) that is faster to
calculate than forming Φ(xi) and then ⟨Φ(xi), Φ(xj)⟩.
▶ Flexibility: We construct functions k(x, x′), for which we know
that they corresponds to inner products after some feature
mapping Φ, but we don’t know how to compute Φ.
3 / 28

4. Kernels
How to use the Kernel Trick
To evaluate a decision function f(x) on an example x, one typically
employs the kernel trick as follows
f(x) = ⟨w, Φ(x)⟩
=
⟨ N∑
i=1
αiΦ(xi), Φ(x)
⟩
=
N∑
i=1
αi ⟨Φ(xi), Φ(x)⟩
=
N∑
i=1
αik(xi, x)
4 / 28

5. How to proof that a function
is a kernel?

6. Kernels
Some Definitions
Definition 1.1 (Positive Definite Kernel)
Let X be a nonempty set. A function k : X × X → C is called a
positive definite if and only if
n∑
i=1
n∑
j=1
cicjk(xi, xj) ≥ 0 (1)
for all n ∈ N, {x1, . . . , xn} ⊆ X and {c1, . . . , cn}.
Unfortunately, there is no common use of the preceding definition in
the literature. Indeed, some authors call positive definite function
positive semi-definite, ans strictly positive definite functions are
sometimes called positive definite.
Note:
For fixed x1, x2, . . . , xn ∈ X, then n × n matrix K := [k(xi, xj)]1≤i,j≤n
is often called the Gram Matrix.
6 / 28

7. Kernels
Mercer Condition
Theorem 1.2
Let X = [a, b] be compact interval and let k : [a, b] × [a, b] → C be
continuous. Then φ is positive definite if and only if
∫ b
a
∫ b
a
c(x)c(y)k(x, y)dxdy ≥ 0 (2)
for each continuous function c : X → C.
7 / 28

8. Kernels
Theorem 1.3 (Symmetric, positive definite functions are kernels)
A function k : X × X → R is a kernel if and only if is symmetric and
positive definite.
8 / 28

9. Kernels
Theorem 1.4
Let k1, k2 . . . are arbitrary positive definite kernels in X × X, where X
is not an empty set.
▶ The set of positive definite kernels is a closed convex cone, that is,
1. If α1, α2 ≥ 0, then α1k1 + α2k2 is positive definitive.
2. If k(x, x′
) := lim
n→∞
kn(x, x′
) exists for all x, x′
then k is positive
definitive.
▶ The product k1.k2 is positive definite kernel.
▶ Assume that for i = 1, 2 ki is a positive definite kernel on Xi × Xi,
where Xi is a nonempty set. Then the tensor product k1 ⊗ k2 and
the direct sum k1 ⊕ k2 are positive definite kernels on
(X1 × X2) × (X1 × X2).
▶ Suppose that Y is not an empty set and let f : Y → X any
arbitrary function then k(x, y) = k1(f(x), f(y)) is a positive
definite kernel over Y × Y .
9 / 28

10. Kernel Families

11. Kernels Kernel Families
Translation Invariant Kernels
Definition 1.5
A translation invariant kernel is given by
K(x, y) = k(x − y) (3)
where k is a even function in Rn, i.e., k(−x) = k(x) for all x in Rn.
11 / 28

12. Kernels Kernel Families
Translation Invariant Kernels
Definition 1.6
A function f : (0, ∞) → R is completely monotonic if it is C∞ and, for
all r > 0 and k ≥ 0,
(−1)k
f(k)
(r) ≥ 0 (4)
Here f(k) denotes the k−th derivative of f.
Theorem 1.7
Let X ⊂ Rn, f : (0, ∞) → R and K : X × X → R be defined by
K(x, y) = f(∥x − y∥2). If f is completely monotonic then K is positive
definite.
12 / 28

13. Kernels Kernel Families
Translation Invariant Kernels
Corollary 1.8
Let c ̸= 0. Then following kernels, defined on a compact domain
X ⊂ Rn, are Mercer Kernels.
▶ Gaussian Kernel or Radial Basis Function (RBF) or
Squared Exponential Kernel (SE)
k(x, y) = exp
(
−
∥x − y∥2
2σ2
)
(5)
▶ Inverse Multiquadratic Kernel
k(x, y) =
(
c2
+ ∥x − y∥2
)−α
, α > 0 (6)
13 / 28

14. Kernels Kernel Families
Polynomial Kernels
k(x, x′
) = (α⟨x, x′
⟩ + c)d
, α > 0, c ≥ 0, d ∈ Z (7)
14 / 28

15. Kernels Kernel Families
Non Mercer Kernels
Example 1.9
Let k : X × X → R defined as
k(x, x′
) =
{
1 , ∥x − x′∥ ≥ 1
0 , in other case
(8)
Suppose that k is a Mercer Kernel and set x1 = 1, x2 = 2 and x3 = 3
then the matrix Kij = k(xi, xj) for 1 ≤ i, j ≤ 3 is
K =


1 1 0
1 1 1
0 1 1

 (9)
then the eigenvalues of K are λ1 = (
√
2 − 1)−1 > 0 and
λ2 = (1 −
√
2) < 0. This is a contradiction because all the eigenvalues
of K are positive then we can conclude that k is not a Mercer Kernel.
15 / 28

16. Kernels Kernel Families
References for Kernels
[3] C. Berg, J. Reus, and P. Ressel. Harmonic Analysis on
Semigroups: Theory of Positive Definite and Related Functions.
Springer Science+Business Media, LLV, 1984.
[9] Felipe Cucker and Ding Xuan Zhou. Learning Theory.
Cambridge University Press, 2007.
[47] Ingo Steinwart and Christmannm Andreas. Support Vector
Machines. 2008.
16 / 28

17. Support Vector Machines

18. Applications SVM
Support Vector Machines
w, x + b = 1
w, x + b = −1
w, x + b = 0
margen
Figure: Linear Support Vector Machine
18 / 28

19. Applications SVM
Primal Problem
Theorem 3.1
The optimization program for the maximum margin classifier is



min
w,b
1
2
∥w∥2
s.a yi(⟨w, xi⟩ + b) ≥ 1, ∀i, 1 ≤ i ≤ m
(10)
19 / 28

20. Applications SVM
Theorem 3.2
Let F a function defined as:
F : Rm
→ R+
w → F(w) =
1
2
∥w∥2
then following affirmations are hold:
1. F is infinitely differential.
2. The gradient of F is ∇F(w) = w.
3. The Hessian of F is ∇2F(w) = Im×m.
4. The Hessian ∇2F(w) is strictly convex.
20 / 28

21. Applications SVM
Theorem 3.3 (The dual problem)
The Dual optimization program of (12) is:



max
α
m∑
i=1
αi −
1
2
m∑
i=1
m∑
j=1
αiαjyiyj⟨xi, xj⟩
s.a αi ≥ 0 ∧
m∑
i=1
αiyi = 0, ∀i, 1 ≤ i ≤ m
(11)
where α = (α1, α2, . . . , αm) and the solution for this dual problem will
be denotated by α∗ = (α∗
1, α∗
2, . . . , α∗
m).
21 / 28

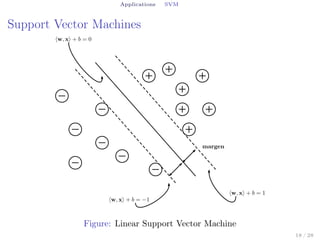
22. Applications SVM
Proof.
The Lagrangianx of the function F is
L(x, b, α) =
1
2
∥w∥2
−
m∑
i=1
αi[yi(⟨w, xi⟩ + b) − 1] (12)
Because of the KKT conditions are hold (F is continuous and
differentiable and the restrictions are also continuous and differentiable)
then we can add the complementary conditions
Stationarity:
∇wL = w −
m∑
i=1
αiyixi = 0 ⇒ w =
m∑
i=1
αiyixi (13)
∇bL = −
m∑
i=1
αiyi = 0 ⇒
m∑
i=1
αiyi = 0 (14)
22 / 28

23. Applications SVM
Primal feasibility:
yi(⟨w, xi⟩ + b) ≥ 1, ∀i ∈ [1, m] (15)
Dual feasibility:
αi ≥ 0, ∀i ∈ [1, m] (16)
Complementary slackness:
αi[yi(⟨w, xi⟩+b)−1] = 0 ⇒ αi = 0∨yi(⟨w, xi⟩+b) = 1, ∀i ∈ [1, m] (17)
L(w, b, α) =
1
2
m∑
i=1
αiyixi
2
−
m∑
i=1
m∑
j=1
αiαjyiyj⟨xi, xj⟩
=− 1
2
∑m
i=1
∑m
j=1 αiαjyiyj⟨xi,xj⟩
−
m∑
i=1
αiyib
=0
+
m∑
i=1
αi
(18)
then
L(w, b, α) =
m∑
i=1
αi −
1
2
m∑
i=1
m∑
j=1
αiαjyiyj⟨xi, xj⟩ (19)
23 / 28

24. Applications SVM
Theorem 3.4
Let G a function defined as:
G: Rm
→ R
α → G(α) = αt
Im×m −
1
2
αt
Aα
where α = (α1, α2, . . . , αm) y A = [yiyj⟨xi, xj⟩]1≤i,j≤m in Rm×m then
the following affirmations are hold:
1. The A is symmetric.
2. The function G is differentiable and
∂G(α)
∂α
= Im×m − Aα.
3. The function G is twice differentiable and
∂2G(α)
∂α2
= −A.
4. The function G is a concave function.
24 / 28

25. Applications SVM
Linear Support Vector Machines
We will called Support Vector Machines to the decision function defined
by
f(x) = sign (⟨w, x⟩ + b) = sign
( m∑
i=1
α∗
i yi⟨xi, x⟩ + b
)
(20)
Where
▶ m is the number of training points.
▶ α∗
i are the lagrange multipliers of the dual problem (13).
25 / 28

26. Applications Non Linear SVM
Non Linear Support Vector Machines
We will called Non Linear Support Vector Machines to the decision
function defined by
f(x) = sign (⟨w, Φ(x)⟩ + b) = sign
( m∑
i=1
α∗
i yi⟨Φ(xi), Φ(x)⟩ + b
)
(21)
Where
▶ m is the number of training points.
▶ α∗
i are the lagrange multipliers of the dual problem (13).
26 / 28

27. Applications Non Linear SVM
Applying the Kernel Trick
Using the kernel trick we can replace ⟨Φ(xi), Φ(x)⟩ by a kernel k(xi, x)
f(x) = sign
( m∑
i=1
α∗
i yik(xi, x) + b
)
(22)
Where
▶ m is the number of training points.
▶ α∗
i are the lagrange multipliers of the dual problem (13).
27 / 28

28. Applications Non Linear SVM
References for Support Vector Machines
[31] Mehryar Mohri, Afshin Rostamizadeh, and Ameet Talwalkar.
Foundations of Machine Learning. The MIT Press, 2012.
28 / 28