The document discusses the estimation and analysis of functional connectomes in cognitive neuroscience, focusing on the strengths and limitations of sparsity in statistical models. Key topics include graphical models, independence structures, challenges in estimating partial correlations, and the impact of multi-subject data on connectome analysis. It emphasizes the importance of sparsity and potential issues with estimation accuracy in the context of brain connectivity modeling.

1. Estimating Functional Connectomes:
Sparsity’s Strength and Limitations
Ga¨el Varoquaux Ssssssskeptical

2. Graphical models in cognitive neuroscience
G Varoquaux 2

3. Functional connectome analysis
Functional regions
G Varoquaux 3

4. Functional connectome analysis
Functional regions
Functional connections
G Varoquaux 3

5. Functional connectome analysis
Functional regions
Functional connections
Variations in connections
G Varoquaux 3

6. Outline
1 Estimating connectomes
2 Comparing connectomes
G Varoquaux 4

7. 1 Estimating connectomes
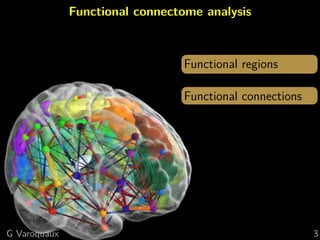
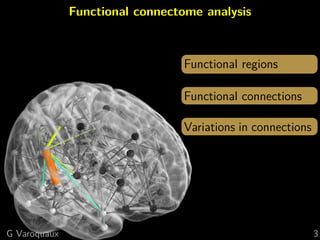
Functional connectome
Graph of interactions between regions
[Varoquaux and Craddock 2013]
G Varoquaux 5

8. 1 Graphical model in cognitive neuroscience
Whish list
Causal links
Directed model:
IPS = V 2 + MT
FEF = IPS + ACC
G Varoquaux 6

9. 1 Graphical model in cognitive neuroscience
Whish list
Causal links
Directed model:
IPS = V 2 + MT
FEF = IPS + ACC
Unreliable delays (HRF)
Few samples
× many signals
Heteroscedastic noise
G Varoquaux 6

10. 1 Graphical model in cognitive neuroscience
Whish list
Causal links
Directed model:
IPS = V 2 + MT
FEF = IPS + ACC
Unreliable delays (HRF)
Few samples
× many signals
Heteroscedastic noise
Independence structure
Knowing IPS, FEF is independent of V2 and MT
G Varoquaux 6

11. 1 From correlations to connectomes
Conditional independence structure?
G Varoquaux 7

12. 1 Probabilistic model for interactions
Simplest data generating process
= multivariate normal:
P(X) ∝ |Σ−1|e−1
2XT Σ−1X
Model parametrized by inverse covariance matrix,
K = Σ−1
: conditional covariances
Goodness of fit:
likelihood of observed covariance ˆΣ in model Σ
L( ˆΣ|K) = log |K| − trace( ˆΣ K)
G Varoquaux 8

13. 1 Graphical structure from correlations
Observations
Covariance
0
1
2
3
4
Diagonal:
signal variance
Direct connections
Inverse covariance
0
1
2
3
4
Diagonal:
node innovation
G Varoquaux 9

14. 1 Independence structure (Markov graph)
Zeros in partial correlations
give conditional independence
Reflects the large-scale
brain interaction structure
G Varoquaux 10

15. 1 Independence structure (Markov graph)
Zeros in partial correlations
give conditional independence
Ill-posed problem:
multi-collinearity
⇒ noisy partial correlations
Independence between nodes makes estimation
of partial correlations well-conditionned.
Chicken and egg problem
G Varoquaux 10

16. 1 Independence structure (Markov graph)
Zeros in partial correlations
give conditional independence
Ill-posed problem:
multi-collinearity
⇒ noisy partial correlations
Independence between nodes makes estimation
of partial correlations well-conditionned.
0
1
2
3
4
0
1
2
3
4
+
Joint estimation:
Sparse inverse covariance
G Varoquaux 10

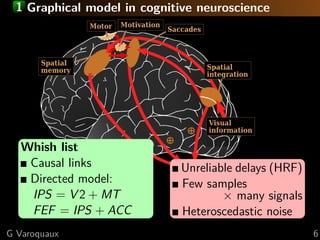
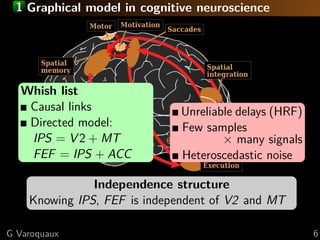
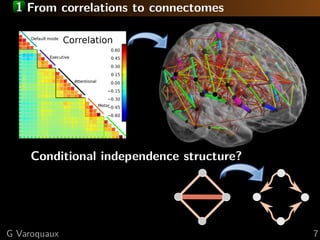
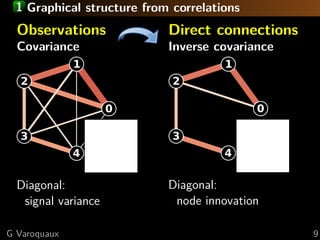
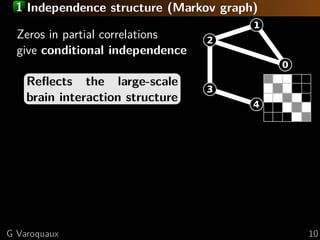
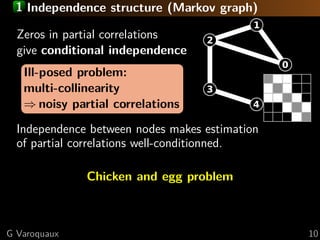
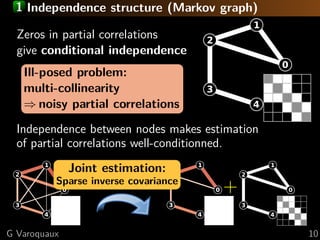
17. 1 Sparse inverse covariance: penalization
[Friedman... 2008, Varoquaux... 2010b, Smith... 2011]
Maximum a posteriori:
Fit models with a penalty
Sparsity ⇒ Lasso-like problem: 1 penalization
K = argmin
K 0
L( ˆΣ|K) + λ 1(K)
Data fit,
Likelihood
Penalization,
x2
x1
G Varoquaux 11

18. 1 Sparse inverse covariance: penalization
[Varoquaux... 2010b]
ˆΣ−1 Sparse
inverse
Likelihood of new data (cross-validation)
Subject data, Σ−1
-57.1
Subject data, sparse inverse 43.0
G Varoquaux 12

19. 1 Limitations of sparsity Sssssskeptical
Theoretical limitation to sparse recovery
Number of samples for s edges, p nodes:
n = O (s + p) log p [Lam and Fan 2009]
High-degree nodes fail [Ravikumar... 2011]
Empirically
Optimal graph
almost dense
2.5 3.0 3.5 4.0
−log10λ
Test-datalikelihood
Sparsity
[Varoquaux... 2012]
Very sparse graphs
don’t fit the data
G Varoquaux 13

20. 1 Multi-subject to overcome subject data scarsity
[Varoquaux... 2010b]
ˆΣ−1 Sparse
inverse
Sparse group
concat
Likelihood of new data (cross-validation)
Subject data, Σ−1
-57.1
Subject data, sparse inverse 43.0
Group concat data, Σ−1
40.6
Group concat data, sparse inverse 41.8
Inter-subject variability
G Varoquaux 14

21. 1 Multi-subject sparsity
[Varoquaux... 2010b]
Common independence structure but different
connection values
{Ks
} = argmin
{Ks 0} s
L( ˆΣs
|Ks
) + λ 21({Ks
})
Multi-subject data fit,
Likelihood
Group-lasso penalization
G Varoquaux 15

22. 1 Multi-subject sparsity
[Varoquaux... 2010b]
Common independence structure but different
connection values
{Ks
} = argmin
{Ks 0} s
L( ˆΣs
|Ks
) + λ 21({Ks
})
Multi-subject data fit,
Likelihood
1 on the connections of
the 2 on the subjects
G Varoquaux 15

23. 1 Multi-subject sparse graphs perform better
[Varoquaux... 2010b]
ˆΣ−1 Sparse
inverse
Population
prior
Likelihood of new data (cross-validation) sparsity
Subject data, Σ−1
-57.1
Subject data, sparse inverse 43.0 60% full
Group concat data, Σ−1
40.6
Group concat data, sparse inverse 41.8 80% full
Group sparse model 45.6 20% full
G Varoquaux 16

24. 1 Independence structure of brain activity
Subject-sparse
estimate
G Varoquaux 17

25. 1 Independence structure of brain activity
Population-
sparse estimate
G Varoquaux 17

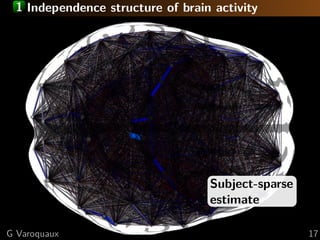
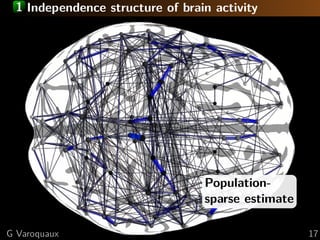
26. 1 Large scale organization: communities
Graph communities
[Eguiluz... 2005]
Non-sparse
Neural communities
G Varoquaux 18

27. 1 Large scale organization: communities
Graph communities
[Eguiluz... 2005]
Group-sparse
Neural communities
= large known functional networks
[Varoquaux... 2010b]
G Varoquaux 18

28. 1 Giving up on sparsity?
Sparsity is finicky
Sensitive hyper-parameter
Slow and unreliable convergence
Unstable set of selected edges
Shrinkage
Softly push partial correlations to zero
ΣShrunk = (1 − λ)ΣMLE + λId
Ledoit-Wolf oracle to set λ
[Ledoit and Wolf 2004]
G Varoquaux 19

29. 2 Comparing connectomes
Functional biomarkers
Population imaging
G Varoquaux 20

30. 2 Failure of univariate approach on correlations
Subject variability spread across correlation matrices
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25Large lesion
dΣ = Σ2 − Σ1 is not definite positive
⇒ not a covariance
Σ does not live in a vector space
G Varoquaux 21

31. 2 Inverse covariance very noisy
Partial correlations are hard to estimate
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25Large lesion
G Varoquaux 22

32. 2 A toy model of differences in connectivity
Two processes with different partial correlations
K1: K1 − K2: Σ1: Σ1 − Σ2:
+ jitter in observed covariance
MSE(K1 − K2): MSE(Σ1 − Σ2):
Non-local effects and non homogeneous noise
G Varoquaux 23

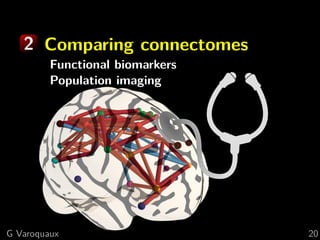
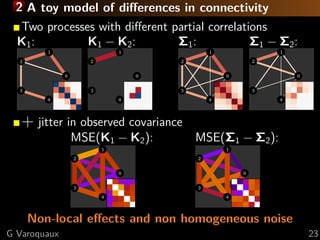
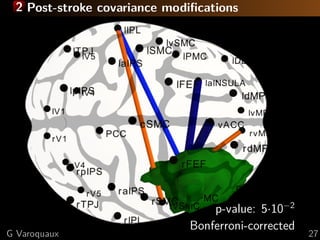
33. 2 Theory: error geometry
Disentangle parameters (edge-level connectivities)
Connectivity matrices form a manifold
⇒ project to tangent space
θ¹
θ²
( )θ¹I
-1
( )θ²I
-1
Estimation error of covariances
Assymptotics given by Fisher matrix [Rao 1945]
Cramer-Rao bounds
G Varoquaux 24

34. 2 Theory: error geometry
Disentangle parameters (edge-level connectivities)
Connectivity matrices form a manifold
⇒ project to tangent space
M
anifold
[Varoquaux... 2010a]
Estimation error of covariances
Assymptotics given by Fisher matrix [Rao 1945]
Defines a metric on a manifold of models
With covariances: Lie-algebra structure [Lenglet... 2006]
G Varoquaux 24

35. 2 Reparametrization for uniform error geometry
Disentangle parameters (edge-level connectivities)
Connectivity matrices form a manifold
⇒ project to tangent space
Controls
Patient
dΣ
M
anifold
Tangent
dΣ = Σ
− 1
/2
Ctrl ΣPatientΣ
− 1
/2
Ctrl
[Varoquaux... 2010a]
G Varoquaux 24

36. 2 Reparametrization for uniform error geometry
The simulations
K1 − K2: Σ1 − Σ2: dΣ: MSE(dΣ):
Semi-local effects and homogeneous noise
G Varoquaux 25

37. 2 Residuals
Correlation matrices: Σ -1.0 0.0 1.0
0 5 10 15 20 25
0
5
0
5
0
5
0 5 10 15 20 25
0
5
10
15
20
25
0 5 10 15 20 25
0
5
10
15
20
25
0 5 10 15 20 25
0
5
10
15
20
25
Residuals: dΣ -1.0 0.0 1.0
0 5 10 15 20 25
0
5
0
5
0
5
Control
0 5 10 15 20 25
0
5
10
15
20
25
Control
0 5 10 15 20 25
0
5
10
15
20
25
Control
0 5 10 15 20 25
0
5
10
15
20
25
Large lesion
G Varoquaux 26

38. 2 Post-stroke covariance modifications
p-value: 5·10−2
Bonferroni-corrected
G Varoquaux 27

39. 2 Prediction from connectomes
RS-fMRI
Functional
connectivity
Time series
2
4
3
1
Diagnosis
ROIs
G Varoquaux 28

40. 2 Prediction from connectomes
Time series
2
RS-fMRI
41
Diagnosis
ROIs Functional
connectivity
3
Connectivity matrix
Correlation
Partial correlations
Tangent space
G Varoquaux 28

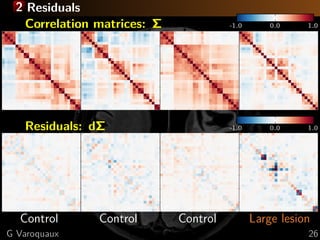
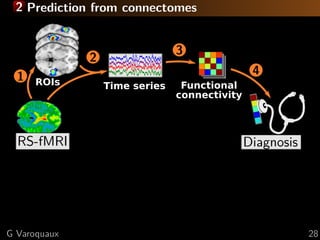
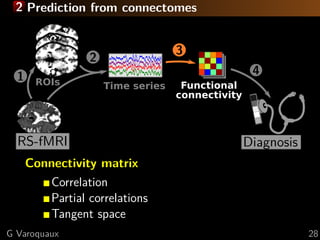
41. 2 Prediction from connectomes
Time series
2
RS-fMRI
41
Diagnosis
ROIs Functional
connectivity
3
Connectivity matrix
Correlation
Partial correlations
Tangent space
Prediction accuracy
Autism
[Abraham2016]
[K. Reddy, Poster 3916]
G Varoquaux 28

42. @GaelVaroquaux
Estimation functional connectomes:
sparsity and beyond
Zeros in inverse covariance give
conditional independance
⇒ sparsity
Shrinkage: simpler, faster
(Ledoit-Wolf)
Tangent space
for comparisons
Controls
Patient
Controls
Patient
Software:
http://nilearn.github.io/ ni

43. References I
V. M. Eguiluz, D. R. Chialvo, G. A. Cecchi, M. Baliki, and
A. V. Apkarian. Scale-free brain functional networks.
Physical review letters, 94:018102, 2005.
J. Friedman, T. Hastie, and R. Tibshirani. Sparse inverse
covariance estimation with the graphical lasso. Biostatistics,
9:432, 2008.
C. Lam and J. Fan. Sparsistency and rates of convergence in
large covariance matrix estimation. Annals of statistics, 37
(6B):4254, 2009.
O. Ledoit and M. Wolf. A well-conditioned estimator for
large-dimensional covariance matrices. J. Multivar. Anal.,
88:365, 2004.

44. References II
C. Lenglet, M. Rousson, R. Deriche, and O. Faugeras.
Statistics on the manifold of multivariate normal
distributions: Theory and application to diffusion tensor
MRI processing. Journal of Mathematical Imaging and
Vision, 25:423, 2006.
C. Rao. Information and accuracy attainable in the estimation
of statistical parameters. Bull. Calcutta Math. Soc., 37:81,
1945.
P. Ravikumar, M. J. Wainwright, G. Raskutti, B. Yu, ...
High-dimensional covariance estimation by minimizing
1-penalized log-determinant divergence. Electronic Journal
of Statistics, 5:935–980, 2011.
S. Smith, K. Miller, G. Salimi-Khorshidi, M. Webster,
C. Beckmann, T. Nichols, J. Ramsey, and M. Woolrich.
Network modelling methods for fMRI. Neuroimage, 54:875,
2011.

45. References III
G. Varoquaux and R. C. Craddock. Learning and comparing
functional connectomes across subjects. NeuroImage, 80:
405, 2013.
G. Varoquaux, F. Baronnet, A. Kleinschmidt, P. Fillard, and
B. Thirion. Detection of brain functional-connectivity
difference in post-stroke patients using group-level
covariance modeling. In MICCAI. 2010a.
G. Varoquaux, A. Gramfort, J. B. Poline, and B. Thirion.
Brain covariance selection: better individual functional
connectivity models using population prior. In NIPS. 2010b.
G. Varoquaux, A. Gramfort, J. B. Poline, and B. Thirion.
Markov models for fMRI correlation structure: is brain
functional connectivity small world, or decomposable into
networks? Journal of Physiology - Paris, 106:212, 2012.