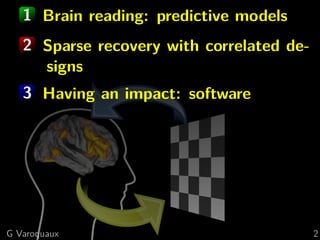
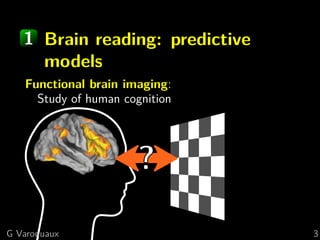
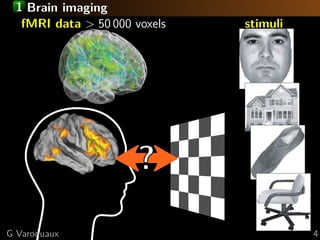
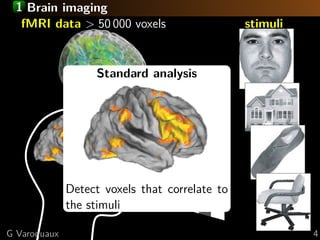
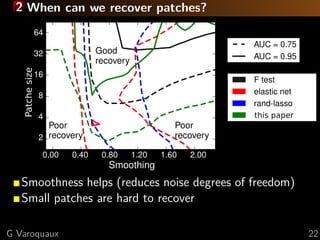
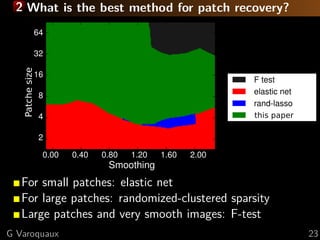
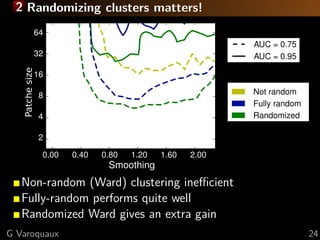
This document discusses techniques for predictive modeling of brain imaging data using statistical learning methods. It presents an approach that combines sparse recovery, randomized clustering, and total variation regularization to predict stimuli from fMRI data with over 50,000 voxels and around 100 samples. The key steps are clustering spatially correlated voxels, running sparse models on the reduced feature set, and accumulating selected features over multiple runs. Simulations show this approach outperforms other methods at recovering brain patches. The document also discusses disseminating research through open source Python libraries like scikit-learn, which has helped popularize machine learning techniques.

1. Brain reading:
Compressive sensing, fMRI,
and statistical learning in Python
Ga¨l Varoquaux
e
INRIA/Parietal

2. 1 Brain reading: predictive models
2 Sparse recovery with correlated de-
signs
3 Having an impact: software
G Varoquaux 2

3. 1 Brain reading: predictive
models
Functional brain imaging:
Study of human cognition
G Varoquaux 3

4. 1 Brain imaging
fMRI data > 50 000 voxels stimuli
G Varoquaux 4

5. 1 Brain imaging
fMRI data > 50 000 voxels stimuli
Standard analysis
Detect voxels that correlate to
the stimuli
G Varoquaux 4

6. 1 Brain reading
Predicting the object category viewed
[Haxby 2001, Distributed and Overlapping
Representations of Faces and Objects in Ventral
Temporal Cortex ]
Supervised learning task
G Varoquaux 5

7. 1 Brain reading
Predicting the object category viewed
[Haxby 2001, Distributed and Overlapping
Representations of Faces and Objects in Ventral
Temporal Cortex ]combinations of voxels to
Find
predict the stimuli
Supervised learning task
Multi-variate statistics
G Varoquaux 5

8. 1 Linear model for fMRI
sign(X w + e) = y
Target
Design
matrix × Coefficients =
Problem size:
p > 50 000
n∼100 per category
G Varoquaux 6

9. 1 Estimation: statistical learning
Inverse problem Minimize an error term:
w = argmin l(y − X w)
ˆ
w
Ill-posed: X is not full rank
Inject prior: regularize
w = argmin l(y − X w) + p(w)
ˆ
w
G Varoquaux 7

10. 1 Estimation: statistical learning
Inverse problem Minimize an error term:
w = argmin l(y − X w)
ˆ
w
Example: Lasso = sparseis not full rank
Ill-posed: X regression
w = argmin y − X w 2 + 1 (w)
ˆ 2
w
1 (w) = i |wi |Inject prior: regularize
w = argmin l(y − X w) + p(w)
ˆ
w
G Varoquaux 7

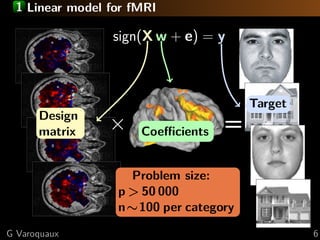
11. 1 TV-penalization to promote regions
[Haxby 2001]
Neuroscientists think in
terms of brain regions
Total-variation penalization
Impose sparsity on the gradient
of the image:
p(w) = 1( w)
[Michel TMI 2011]
G Varoquaux 8

12. 1 Prediction with logistic regression - TV
w = argmin l(y − X w) + p(w)
ˆ
w
l: least-square or logistic-regression p: TV
Optimization: proximal gradient (FISTA)
- Gradient descent on l (smooth term)
- Projections on TV
Prediction performance:
Feature screening + SVC 0.77
Sparse regression 0.78
Total Variation 0.84
(explained variance)
G Varoquaux 9

13. 1 Prediction with logistic regression - TV
wStandard l(y − X w) + p(w)
ˆ = argmin analysis
w
l: least-square or logistic-regression p: TV
Optimization: proximal gradient (FISTA)
- Gradient descent on l (smooth term)
- Projections on TV
Prediction performance:
Feature screening + SVC 0.77
Sparse regression 0.78
Total Variation 0.84
(explained variance)
G Varoquaux 9

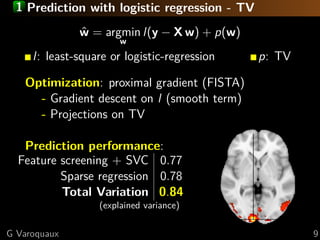
14. 1 Standard analysis or predictive modeling?
Predicting the object category viewed
[Haxby 2001, Distributed and Overlapping
Representations of Faces and Objects in Ventral
Temporal Cortex ]
Take home message:
brain regions, not prediction
G Varoquaux 10

15. 1 Standard analysis or predictive modeling?
Recovery rather than prediction
G Varoquaux 11

16. 1 Good prediction = good recovery
Ground truth
Simulations
Ground truth
Lasso
Prediction: 0.78
Recovery: 0.429
SVM
Prediction: 0.71
Recovery: 0.486
Need a method suited for recovery
G Varoquaux 12

17. 1 Brain mapping: a statistical perspective
Small sample linear model estimation
Random correlated design
× =
Problem size:
p > 50 000
n∼100 per category
G Varoquaux 13

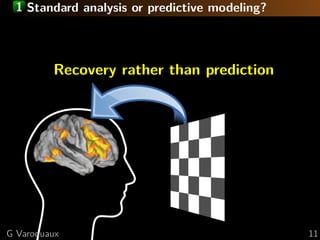
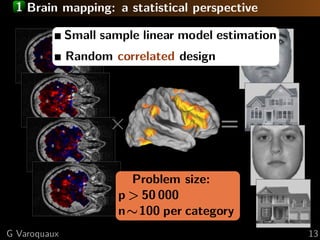
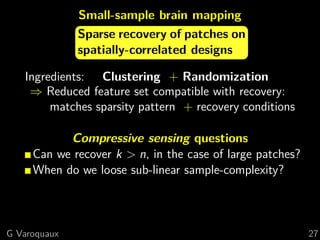
18. 1 Brain mapping: a statistical perspective
Small sample linear model estimation
Random correlated design
Estimation strategy
Standard approach: univariate statistics
×
Multiple comparisons problem
⇒ statistical power ∝ 1/p
=
We want sub-linear sample complexity
⇒ non-rotationally-invariant estimators
e.g. 1 penalization
[ Ng, 2004 Feature selection, 1 vs. 2 regularization,
and rotational invariance ]
G Varoquaux 13

19. 1 Brain mapping as a sparse recovery task
Recovering brain regions
G Varoquaux 14

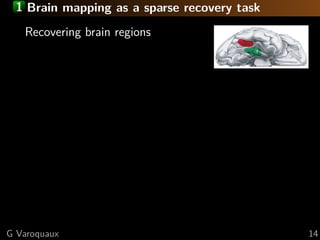
20. 1 Brain mapping as a sparse recovery task
Recovering k non-zero coefficients
nmin ∼ 2 k log p
Restricted-isometry-like property:
The design matrix is well-conditioned [Candes 2006]
on sub-matrices of size > k [Tropp 2004]
[Wainwright 2009]
Mutual incoherence:
Relevant features S and irrelevant
ones S are not too correlated
Violated by spatial
correlations in our design
lasso: 23 non-zeros
G Varoquaux 14

21. 1 Randomized sparsity
[Meinshausen and Buhlmann 2010, Bach 2008]
Perturb the design matrix:
Subsample the data
Randomly rescale features
+ Run sparse estimator
Keep features that are often selected
⇒ Good recovery without mutual incoherence
But RIP-like condition
Cannot recover large
correlated groups
For m correlated features,
selection frequency divided by m
G Varoquaux 15

22. 2 Sparse recovery with
correlated designs
Not enough samples: nmin ∼ 2 k log p
Spatial correlations
G Varoquaux 16

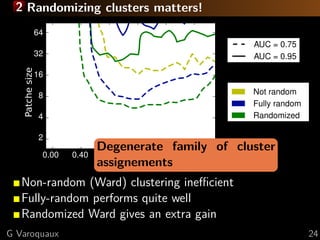
23. 2 Sparse recovery with
correlated designs
Combining
Clustering
Sparsity
[Varoquaux ICML 2012]
G Varoquaux 16

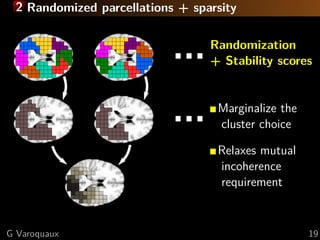
24. 2 Brain parcellations
Spatially-connected hierarchical clustering
⇒ reduces voxel numbers [Michel Pat Rec 2011]
Replace features by corresponding cluster average
+ Use a supervised learner on reduced problem
Cluster choice sub-optimal for regression
G Varoquaux 17

25. 2 Brain parcellations + sparsity
Hypothesis: clustering compatible with support(w)
Benefits of clustering
Reduced k and p
⇒ n > nmin : good side of the “sharp threshold”
Cluster together correlated features
⇒ Improves RIP-like conditions
Recovery possible on reduced features
G Varoquaux 18

26. 2 Randomized parcellations + sparsity
Randomization
+ Stability scores
Marginalize the
cluster choice
Relaxes mutual
incoherence
requirement
G Varoquaux 19

27. 2 Algorithm
1 set n clusters and sparsity by cross-validation
2 loop: perturb randomly data
3 clustering to form reduced features
4 sparse linear model on reduced features
5 accumulate non-zero features
6 threshold map of apparition counts
G Varoquaux 20

28. 2 Simulations
p = 2048, k = 64, n = 256 (nmin > 1000)
Weights w: patches of varying size
Design matrix: 2D Gaussian random images of
varying smoothness
Estimators
Randomized lasso Our approach
Elastic Net Univariate F test
Parameters set by cross-validation
Performance metric
Recovery seen as a 2-class problem
⇒ Report AUC of the precision-recall curve
G Varoquaux 21

29. 2 When can we recover patches?
Smoothness helps (reduces noise degrees of freedom)
Small patches are hard to recover
G Varoquaux 22

30. 2 What is the best method for patch recovery?
For small patches: elastic net
For large patches: randomized-clustered sparsity
Large patches and very smooth images: F-test
G Varoquaux 23

31. 2 Randomizing clusters matters!
Non-random (Ward) clustering inefficient
Fully-random performs quite well
Randomized Ward gives an extra gain
G Varoquaux 24

32. 2 Randomizing clusters matters!
Degenerate family of cluster
assignements
Non-random (Ward) clustering inefficient
Fully-random performs quite well
Randomized Ward gives an extra gain
G Varoquaux 24

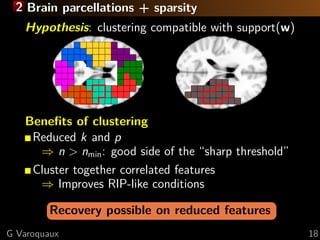
33. 2 fMRI: face vs house discrimination [Haxby 2001]
F-scores
L R
L R
y=-31 x=17
z=-17
G Varoquaux 25

34. 2 fMRI: face vs house discrimination [Haxby 2001]
1 Logistic
L R
L R
y=-31 x=17
z=-17
G Varoquaux 25

35. 2 fMRI: face vs house discrimination [Haxby 2001]
Randomized 1 Logistic
L R
L R
y=-31 x=17
z=-17
G Varoquaux 25

36. 2 fMRI: face vs house discrimination [Haxby 2001]
Randomized Clustered 1 Logistic
L R
L R
y=-31 x=17
z=-17
G Varoquaux 25

37. 2 fMRI: face vs house discrimination [Haxby 2001]
F-scores
L R
L R
y=-31 x=17
z=-17
G Varoquaux 25

38. 2 Predictive model on selected features
Object recognition [Haxby 2001]
Using recovered features improves prediction
G Varoquaux 26

39. Small-sample brain mapping
Sparse recovery of patches on
spatially-correlated designs
Ingredients: Clustering + Randomization
⇒ Reduced feature set compatible with recovery:
matches sparsity pattern + recovery conditions
Compressive sensing questions
Can we recover k > n, in the case of large patches?
When do we loose sub-linear sample-complexity?
G Varoquaux 27

40. 3 Having an impact: software
How to we reach our target
audience (neuroscientists)?
How do we disseminate our ideas?
How do we facilitate new ideas?
G Varoquaux 28

41. 3 Python as a scientific environment
General purpose
Easy, readable syntax
Interactive (ipython)
Great scientific libraries (numpy, scipy, matplotlib...)
G Varoquaux 29

42. 3 Growing a software stack
Code lines are costly
⇒ Open source + community driven
Need quality and impact
⇒ Focus on the general purpose libraries first
Scikit-learn: machine learning in Python
http://scikit-learn.org
G Varoquaux 30

43. 3 scikit-learn: machine learning in Python
Technical choices
Prefer Python or Cython, focus on readability
Documentation and examples are paramount
Little object-oriented design. Opt for simplicity
Prefer algorithms to framework
Code quality: consistency and testing
G Varoquaux 31

44. 3 scikit-learn: machine learning in Python
API
Inputs are numpy arrays
Learn a model from the data:
estimator.fit(X train, Y train)
Predict using learned model
estimator.predict(X test)
Test goodness of fit
estimator.score(X test, y test)
Apply change of representation
estimator.transform(X, y)
G Varoquaux 32

45. 3 scikit-learn: machine learning in Python
Computational performance
scikit-learn mlpy pybrain pymvpa mdp shogun
SVM 5.2 9.47 17.5 11.52 40.48 5.63
LARS 1.17 105.3 - 37.35 - -
Elastic Net 0.52 73.7 - 1.44 - -
kNN 0.57 1.41 - 0.56 0.58 1.36
PCA 0.18 - - 8.93 0.47 0.33
k-Means 1.34 0.79 ∞ - 35.75 0.68
Algorithms rather than low-level optimization
convex optimization + machine learning
Avoid memory copies
G Varoquaux 33

46. 3 scikit-learn: machine learning in Python
Community
163 contributors since 2008, 397 github forks
25 contributors in latest release (3 months span)
Why this success?
Trendy topic?
Low barrier of entry
Friendly and very skilled mailing list
Credit to people
G Varoquaux 34

47. 3 Research code = software library
Factor 10 in time investment
Corner cases in algorithm (numerical stability)
Multiple platforms and library versions (Blas )
Documentation
Making it simpler (and get less educated users)
User and developer support ( ∼ 100 mails/day)
Exhausting,
but has impact on science and society
G Varoquaux 35

48. 3 Research code = software library
Factor 10 in time investment
CornerTechnical + scientific tradeoffs
cases in algorithm (numerical stability)
Multiple platforms andof use rather than speed
Ease of install/ease library versions (Blas )
Documentation science”
Focus on “old
Making it simpler (and get less educatednot
Nice publications and theorems are users)
a recipe for useful code
User and developer support ( ∼ 100 mails/day)
Exhausting,
but has impact on science and society
G Varoquaux 35

49. Statistical learning to study brain function
Spatial regularization for
predictive models
Total variation
Compressive-sensing approach
Sparsity + randomized
clustering for correlated designs
Machine learning in Python
Huge impact
Post-doc positions available
G Varoquaux 36

50. Bibliography
[Michel TMI 2011] V. Michel, et al., Total variation regularization for
fMRI-based prediction of behaviour, IEEE Transactions in medical
imaging (2011)
http://hal.inria.fr/inria-00563468/en
[Varoquaux ICML 2012] G. Varoquaux, A. Gramfort, B. Thirion
Small-sample brain mapping: sparse recovery on spatially correlated
designs with randomization and clustering, ICML (2012)
http://hal.inria.fr/hal-00705192/en
[Michel Pat Rec 2011] V. Michel, et al., A supervised clustering approach
for fMRI-based inference of brain states, Pattern Recognition (2011)
http://hal.inria.fr/inria-00589201/en
[Pedregosa ICML 2011] F. Pedregosa, el al., Scikit-learn: machine
learning in Python, JMRL (2011)
http://hal.inria.fr/hal-00650905/en
G Varoquaux 37