This document discusses properties of triangles, including the angle bisector theorem and similarity of triangles. It provides proofs of several geometry theorems related to ratios of sides and areas of similar triangles. Some key points: - The ratio of corresponding sides of two similar triangles is equal to the ratio of their areas. - If the ratio of corresponding sides of two triangles is r:s, then the ratio of their areas is r^2:s^2. - Medians, angle bisectors, and perpendicular bisectors exhibit properties when used to prove similarity.

1. CH 6
TRIANGLES
ANGLE BISECTOR THEOREM
+
EX 6.4 Q1 AND Q2

2. In the figure, PS is the bisector of ∠QPR of Δ PQR. Prove that
𝑸𝑺
𝑺𝑹
=
𝑷𝑸
𝑷𝑹
Sol. We have ΔPQR in which PS is the bisector of ∠QPR
∠QPS = ∠RPS
Let us draw RT || PS to meet QP produced at T, such that
∠1 = ∠RPS [Alternate angles]
Also ∠3 = ∠QPS [Corresponding angles]
But ∠RPS = ∠QPS [Given]
∠1 = ∠3
⇒ PT = PR [Equal sides of a triangle opposite to equal angles]
Now, in ΔQRT,
∠PR || RT [By construction]
Using the Basic Proportionality Theorem, we have:
⇒
𝑸𝑺
𝑺𝑹
=
𝑷𝑸
𝑷𝑻
⇒
𝑸𝑺
𝑺𝑹
=
𝑷𝑸
𝑷𝑹
[SINCE PT=PR]

3. In the figure, D is a point on side BC of ΔABC such that
𝑩𝑫
𝑪𝑫
=
𝑨𝑩
𝑨𝑪
. Prove that AD is the bisector of
∠BAC.
Sol. Let us produce BA to E such that AE = AC, Join EC.
Since,
𝐵𝐷
𝐶𝐷
=
𝐴𝐵
𝐴𝐶
[Given]
But AC = AE [ by construction]
⇒
𝐵𝐷
𝐶𝐷
=
𝐴𝐵
𝐴𝐸
Now in ∆ABC , Since
𝐵𝐷
𝐶𝐷
=
𝐴𝐵
𝐴𝐸
AD II CE [by the converse of Basic Proportionality theorem]
And BE is a transversal,
∠BAD = ∠AEC [Corresponding angles] ...(1)
Also ∠CAD = ∠ACE [Alternate angles] ...(2)
Since, AC = AE
∴ Their opposite sides are equal
⇒∠AEC = ∠ACE ...(3)
From (1) and (3), we have
∠BAD = ∠ACE ...(4)
From (2) and (4), we have
∠BAD = ∠CAD
⇒ AD is bisector of ∠BAC.

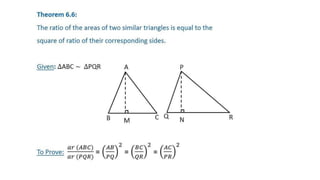
5. EXERCISE 6.4
1. Let ΔABC ~ ΔDEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.
Sol. We have
ar (ΔABC) = 64 cm2
ar (ΔDEF) = 121 cm2 and EF = 15.4 cm
ΔABC ~ ΔDEF [Given]
Since, the ratio of areas of two similar
triangles is equal to the square of, the
ratio of their corresponding sides.

6. 2. Diagonals of a trapezium ABCD With AB || DC intersect each other at the point O. If AB = 2 CD, find
the ratio of the areas of triangles AOB and COD.
Sol. We have in trap. ABCD, AB || DC.
Diagonals AC and BD intersect at O.
In ΔAOB and ΔCOD
∠AOB = ∠COD, [Vertically opposite angles]
∠OAB = ∠OCD, [Alternate angles]
∴Using AA criterion of similarity, we have:
ΔAOB ~ ΔCOD
Since, the ratio of areas of two similar
triangles is equal to the square of, the
ratio of their corresponding sides.

7. 3. In the figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that
Sol. We have:
ΔABC and ΔDBC are on the same base BC. Also BC and
AD intersect at O.
Let us draw AE ⊥ BC and DF ⊥ BC.
In ΔAOE, ΔAEO = 90° and
In ΔDOF, ΔDFO = 90°
∴∠AEO = ∠DFO ...(1)
Also, ∠AOE = ∠ DOF ...(2) [Vertically Opposite Angles]
∴ From (1) and (2),
ΔAOE ~ ΔDOF [By AA similarity]
∴ Their corresponding sides are proportional

8. 4. If the areas of two similar triangles are equal, prove that they are congruent.
Sol. We have ΔABC and ΔDEF, such that ΔABC ~ ΔDEF and
ar(ΔABC) = ar (ΔDEF).
Since, the ratio of areas of two similar triangles is equal to the square of,
the ratio of their corresponding sides.

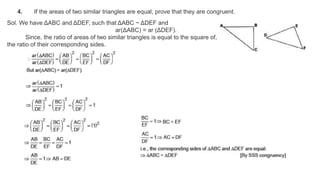
9. 5. D, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC. Find the ratio of the areas
of ΔDEF and ΔABC.
Sol. We have a ΔABC in which D, E and F are mid points of AB, AC and
BC respectively. D, E and F are joined to form ΔDEF.
Now, D is mid-point of AB
∴ Using the converse of the Basic Proportionality Theorem, we have
DE || BC
⇒∠ADE = ∠ABC ...(3) [Corresponding angles]
Also ∠AED = ∠ACE ...(4) [Corresponding angles]
Now from (3) and (4), we have
ΔABC ~ ∠DEF [Using AA similarity]
Since, the ratio of areas of two similar triangles is equal to
the square of, the ratio of their corresponding sides.

11. 6. Prove that the ratio of the areas of two similar triangle is equal to the square of the ratio of
their corresponding medians.
Sol. We have two triangles ABC and DEF such that
ΔABC ~ ΔDEF
AM and DN are medians corresponding to BC and EF respectively.
ΔABC ~ ΔDEF
∴ The ratio of their areas is equal to the square of the ratio of their corresponding sides.

12. 7. Prove that the area of an equilateral triangle described on one side of a square is equal to half the
area o the equilateral triangle described on one of its diagonals.
Sol. We have a square ABCD, whose diagonal AC. Equilateral ΔBQC is described on
the side BC and another equilateral ΔAPC is described on the diagonal AC.
All equilateral triangles are similar.
∴ΔAPC ~ ΔBQC
∴The ratio of they areas is equal to the square of the ratio of their corresponding sides.

13. 8. ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of
triangles ABC and BDE is
(A) 2 : 1 (B) 1 : 2 (C) 4 : 1 (D) 1 : 4
Sol. We have an equilateral ΔABC and D is the midpoint of BC. DE is drawn such that BDE is
also an equilateral triangle.
Since, all equilateral triangles-are similar,
∴ΔABC ~ ΔBDE
⇒The ratio of their areas is, equal to the square of the ratio of their corresponding sides.
From (1) and (2), we have:

14. 9. Sides of two similar triangles are in the ratio 4: 9. Areas of these triangles are in the ratio
(A) 2 :13 (B) 4 : 9 (C) 81 : 16 (D) 16 : 81
Sol. We have two similar triangles such that the ratio of their corresponding sides is 4 : 9
∴ The ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding sides.