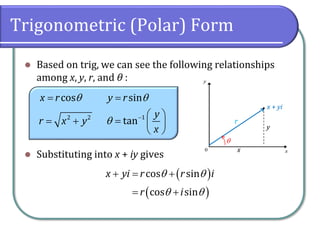
This document discusses polar form of complex numbers. It defines polar form as representing a complex number using trigonometric functions based on the distance r from the origin and the angle θ. The document provides formulas for converting between polar (trigonometric) form and rectangular form. Examples are given of adding complex numbers graphically on the complex plane as well as converting numbers between polar and rectangular form using trigonometric identities and calculator approximations when needed. Students are assigned practice problems converting complex numbers between forms.

1. 8.5 Polar Form
Chapter 8 Applications of Trigonometry

2. Concepts and Objectives
⚫ Trigonometric (Polar) Form
⚫ Complex plane and vector representation
⚫ Converting between trigonometric and rectangular
form

3. The Complex Plane
⚫ Unlike real numbers, complex numbers cannot be put in
order. One way to organize and illustrate them is by
using a modified coordinate system.
⚫ To graph a complex number such as 2 – 3i, the
horizontal axis is called the real axis and the vertical
axis is the imaginary axis.
Complex numbers can be graphed
in this complex plane. Each
complex number a + bi
determines a unique position
vector with initial point (0, 0) and
terminal point (a, b).
2
–3
2 – 3i

4. The Complex Plane (cont.)
⚫ This geometric representation is the reason a + bi is
called the rectangular form of a complex number.
⚫ Recall that to find the sum of two complex numbers, add
the real portions and then add the imaginary parts.
⚫ Example:
⚫ Graphically, the sum of two complex numbers is
represented by the vector that is the resultant of the
vectors corresponding to the two numbers
( ) ( ) ( ) ( )+ + + = + + + = +4 1 3 4 1 3 5 4i i i i i

5. The Complex Plane (cont.)
⚫ Example: Find the sum of 6 – 2i and –4 – 3i. Graph both
complex numbers and their resultant.
( ) ( )6 2 4 3 2 5i i i− + − − = −
–4 – 3i
6 – 2i
2 – 5i

6. Trigonometric (Polar) Form
⚫ Based on trig, we can see the following relationships
among x, y, r, and θ :
⚫ Substituting into x + iy gives
x
y
x + yi
r

cosx r = siny r =
2 2
r x y= + 1
tan
y
x
 −  
=  
 
( )
( )
cos sin
cos sin
x yi r r i
r i
 
 
+ = +
= +

7. Polar Form (cont.)
⚫ The expression is called the
trigonometric form (or polar form) of the complex
number x + yi.
⚫ The expression is sometimes abbreviated
cis θ. Using this notation, is written
r cis θ.
( )cos sinr i +
cos sini +
( )cos sinr i +

8. Polar to Rectangular Form
⚫ Example: Express in rectangular
form.
Using the unit circle from section 6.2, we can list the
degree measures as well as the radian measures and see
that for 300°,
Substituting, we get
( )2 cos300 sin300i+ 
1 3
cos300 and sin300
2 2
 =  = −
( )
1 3
2 cos300 sin300 2
2 2
1 3
i i
i
 
+  = − 
 
= −

9. Rectangular to Polar Form
1. Determine the quadrant of x + yi, sketching a graph in
the complex plane if necessary.
2. Find r by using the equation .
3. Find θ by using the equation .
4. If θ isn’t in the right quadrant (step 1), you may need to
add either 180° or 360° to get the correct angle.
2 2
r x y= +
1
tan
y
x
 −  
=  
 

10. Rectangular to Polar Form (cont.)
⚫ Example: Write in polar form.
1. With a negative x and a positive y, the angle will be in
quadrant II.
2.
3.
4. This is in quadrant IV, so to find its equivalent in QII, we
add 180°: –30 + 180 = 150°
3 i− +
( )
2
2
3 1 4 2r = − + = =
1 1
tan 30
3
 −  
= = −  
− 

11. Rectangular to Polar Form (cont.)
⚫ Now that we have r and θ, we can write the polar form:
( )2 cos150 sin150 or 2 cis 150i+  

12. Calculator Approximations
⚫ Examples: Write each complex number in its alternate
form, using calculator approximations as necessary.
(a) 6 cis 115° (b) 5 – 4i
(a) ( )6 cis 115 6 cos115 sin115
6cos115 6 sin115
2.5357 5.4378
i
i
i
 = + 
= + 
= − +

13. Calculator Approximations
⚫ Examples: Write each complex number in its alternate
form, using calculator approximations as necessary.
(a) 6 cis 115° (b) 5 – 4i
(b)
The angle is in QIV, so we add 360 and θ = 321.34°
( )
22
5 4 41r = + − = 1 4
tan 38.66
5
 −  
= − = −  
 
41 cis 321.34 or 6.403 cis 321.34 

14. Classwork
⚫ Page 788: 10-20 (even); page 771: 30-36 (even), 50, 52;
page 760: 66-70 (even), 76