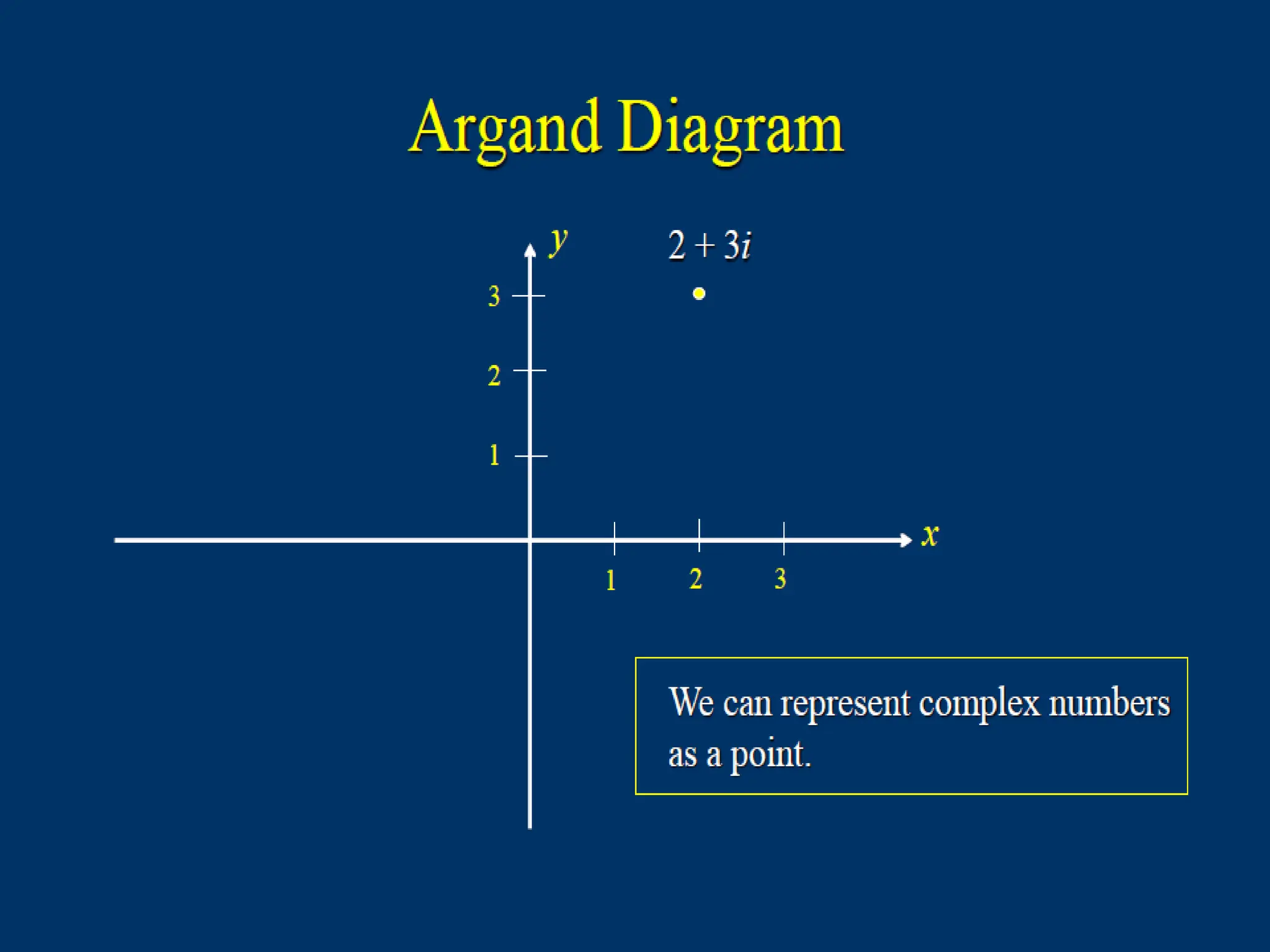
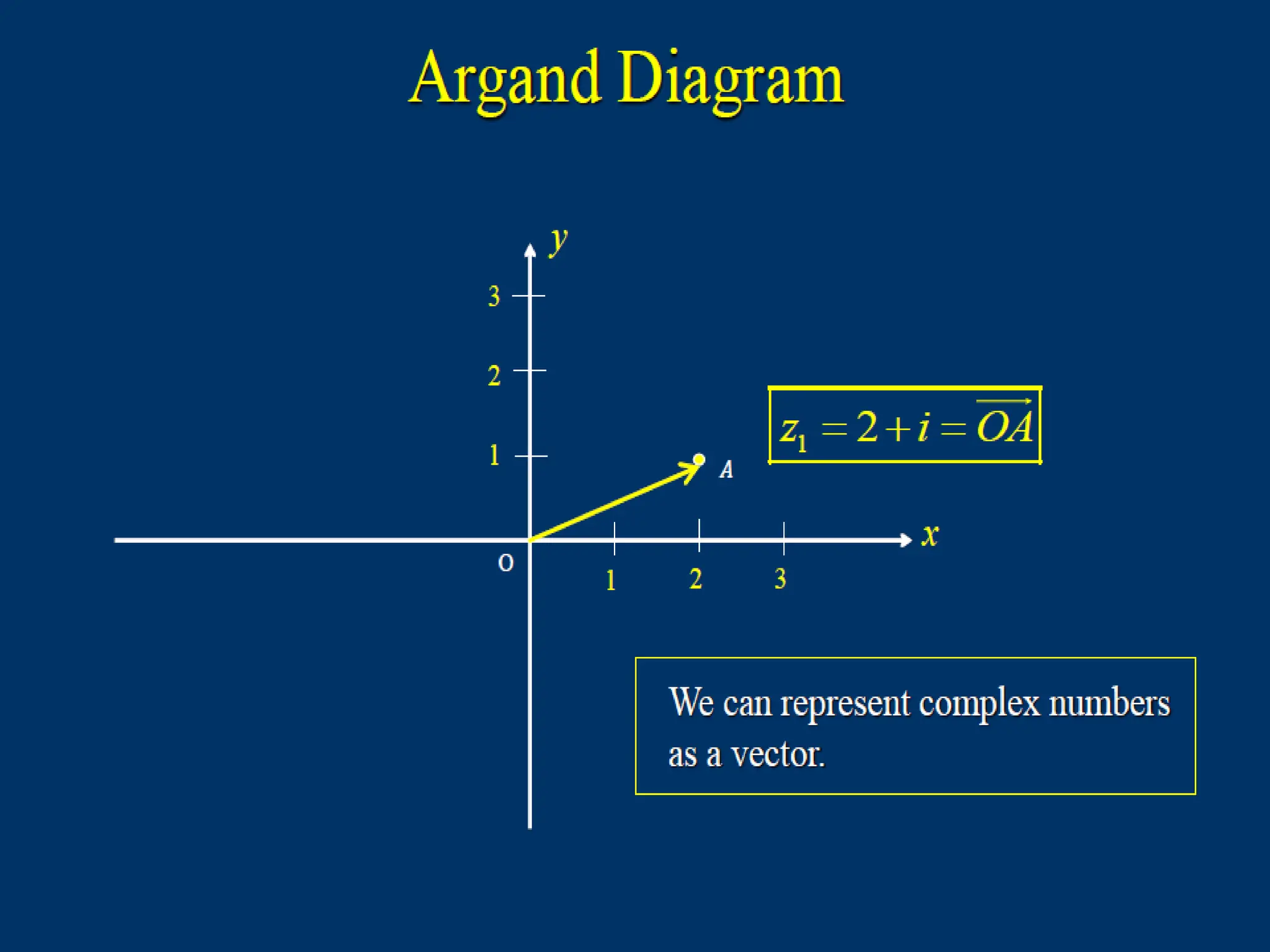
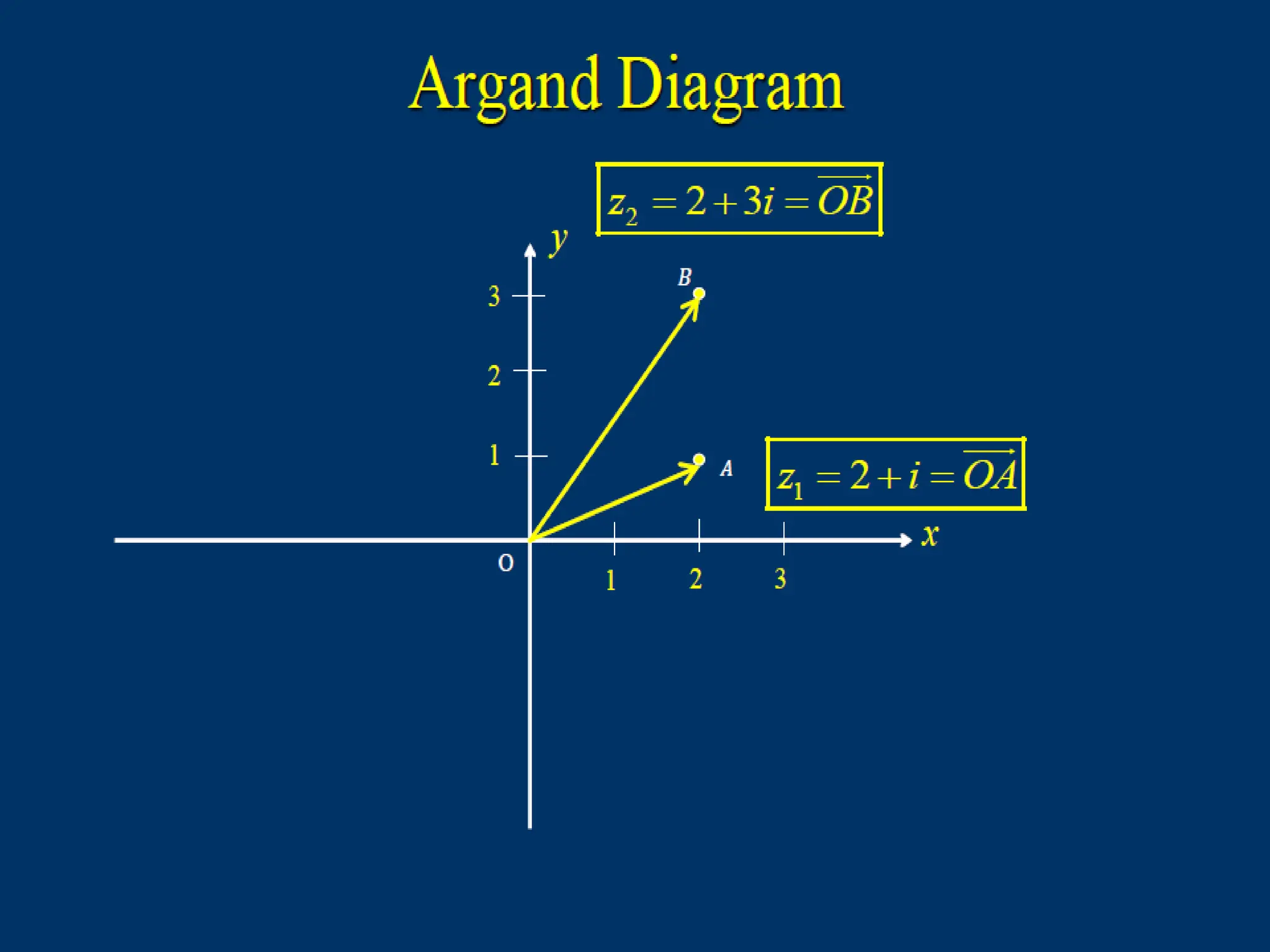
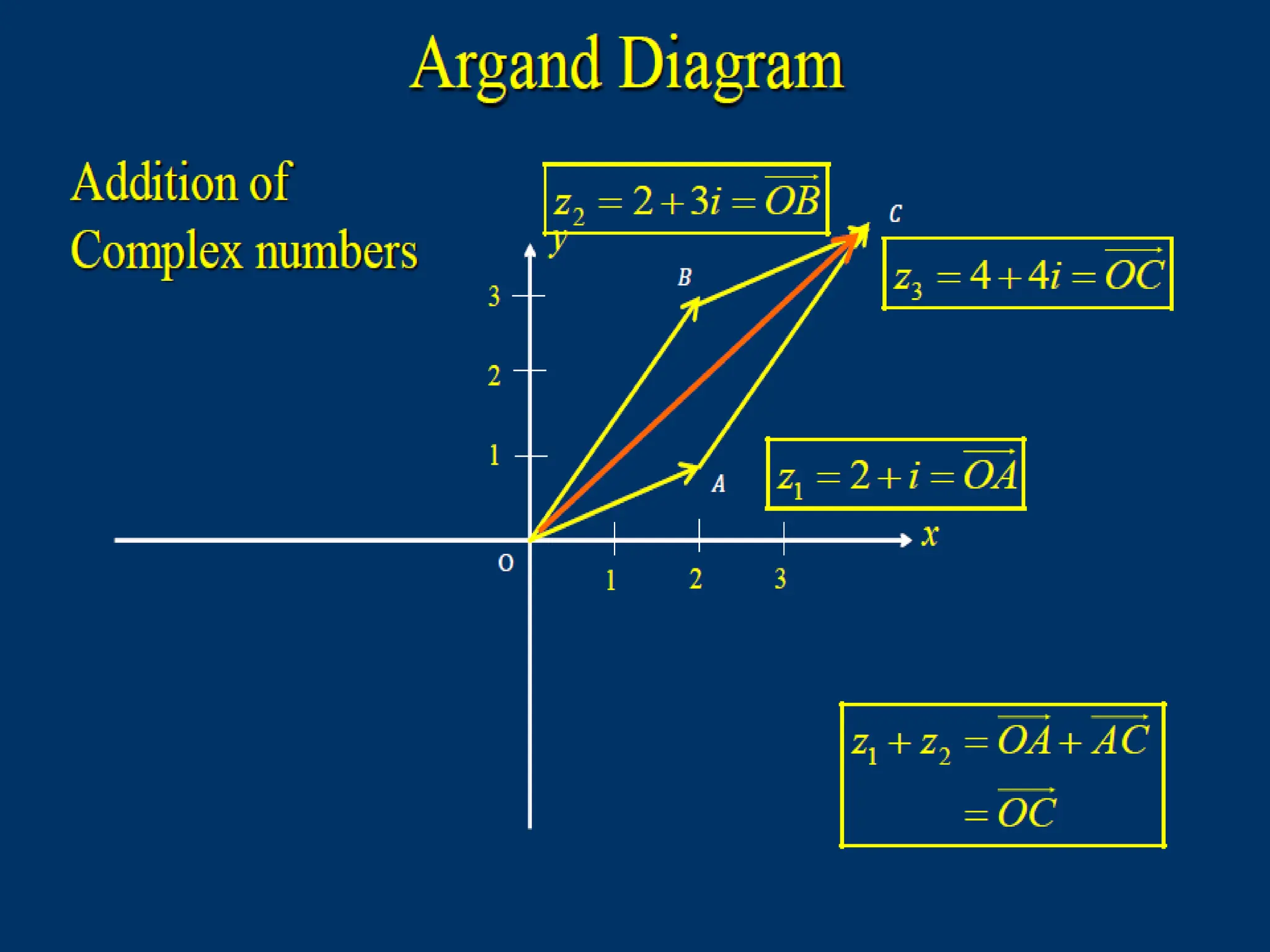
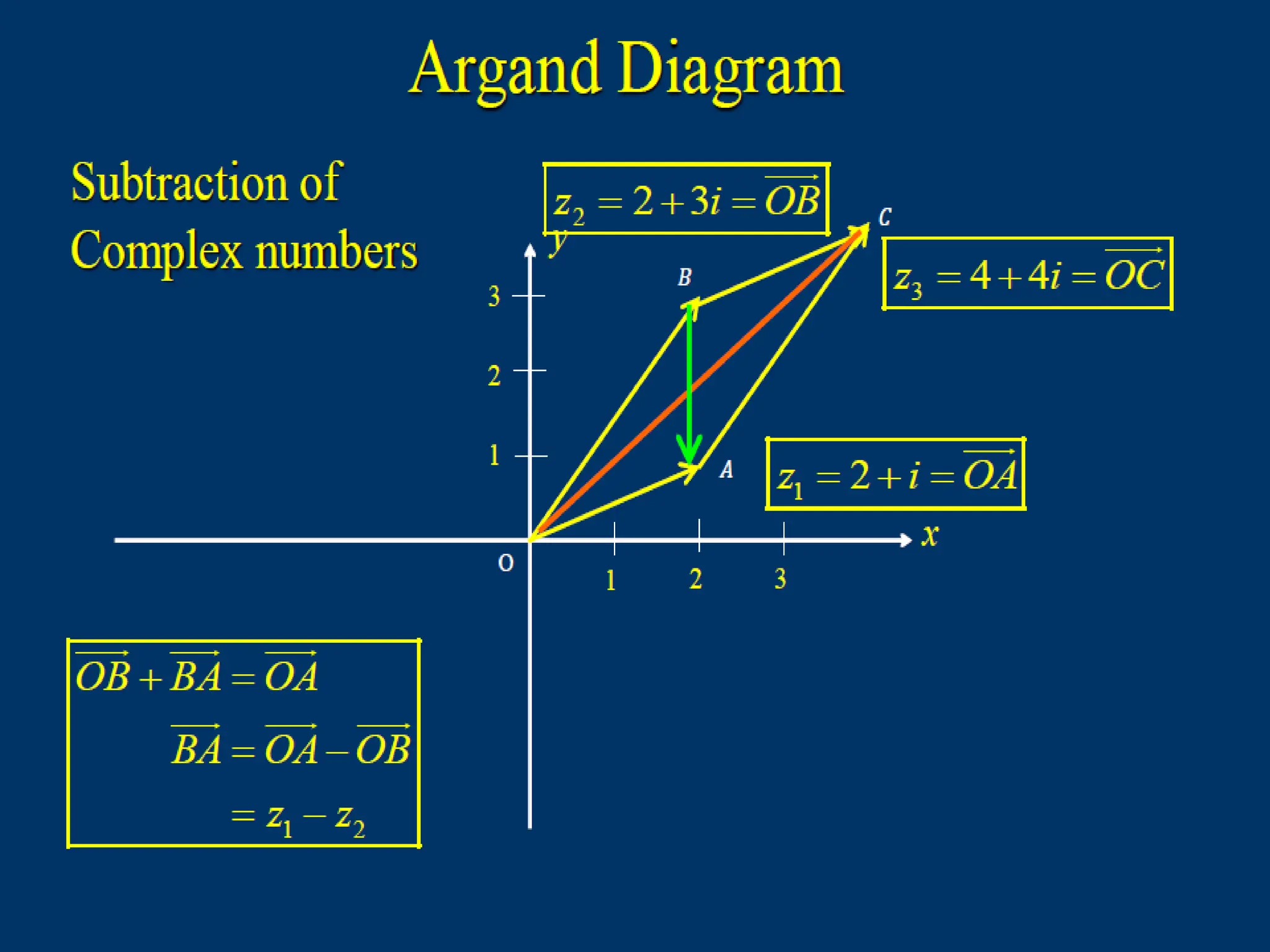
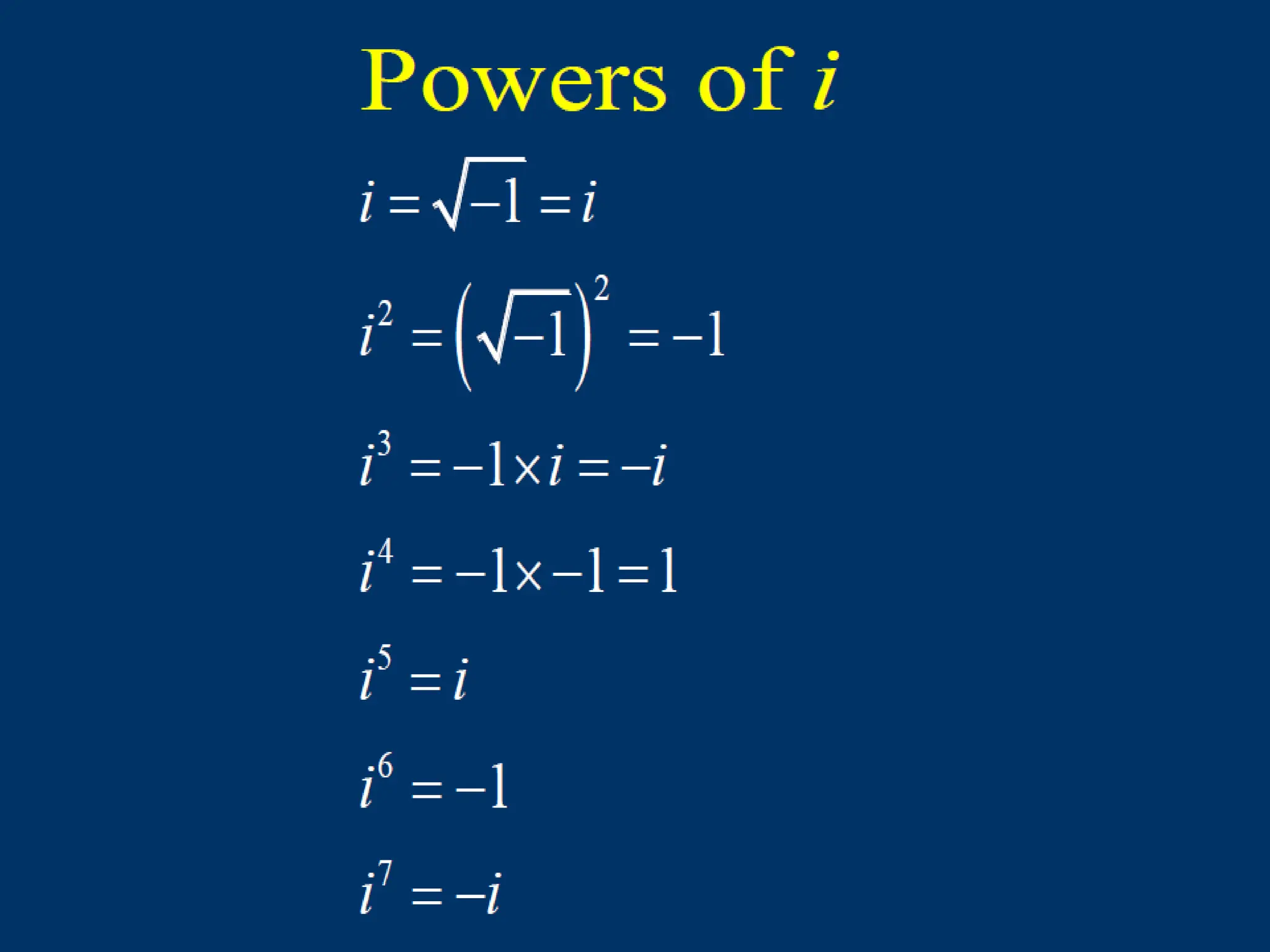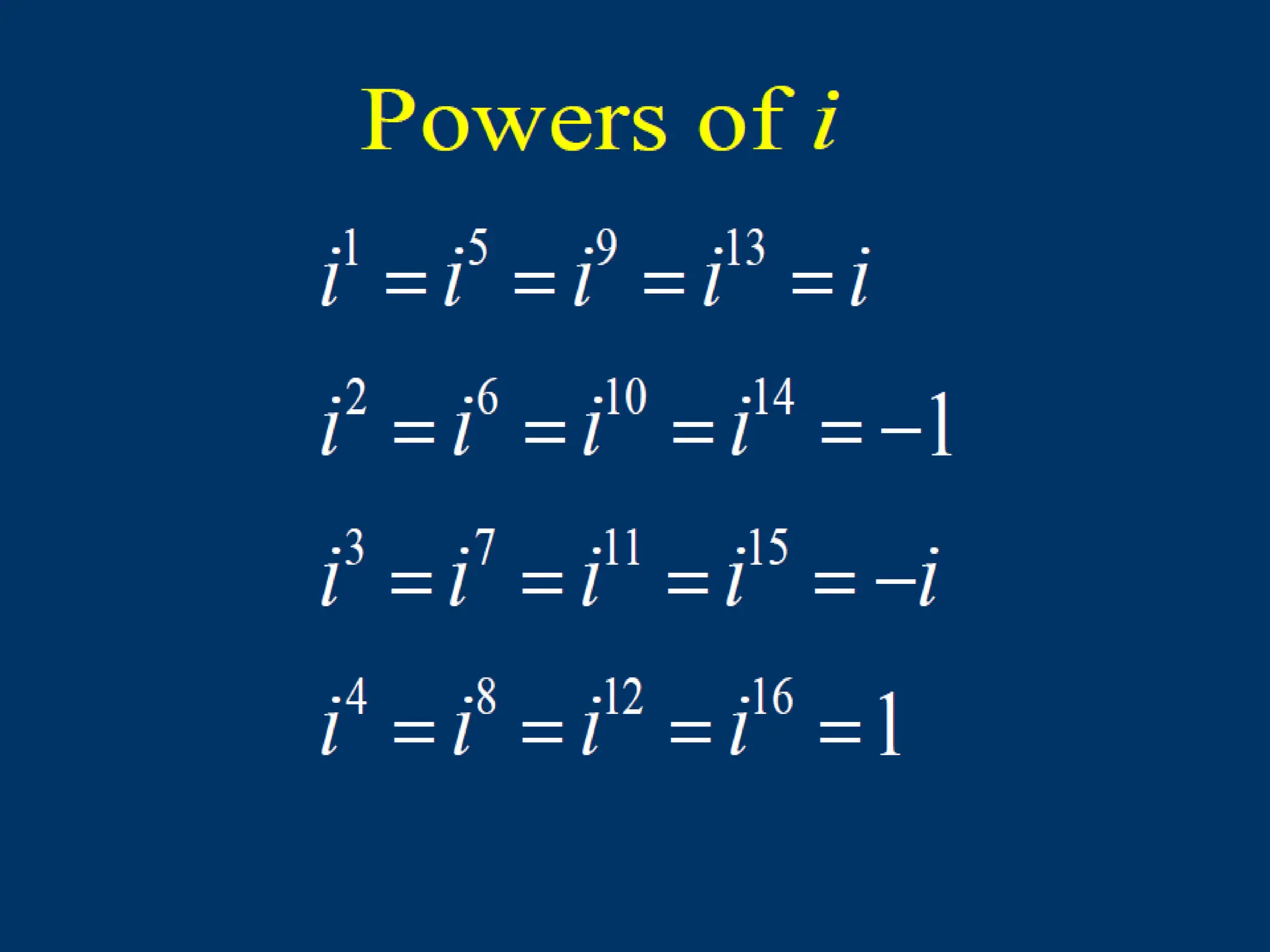The document explains the representation and plotting of complex numbers in the complex plane, detailing the real and imaginary axes. It distinguishes between rectangular and polar forms of complex numbers and provides examples of calculating the modulus and converting complex numbers into polar form. Additionally, it illustrates the process of finding the polar coordinates from rectangular coordinates and how to express complex numbers accordingly.

1. Polar Form of a Complex Number
Dr. Maria Athar

9. The Complex Plane
•A complex number z = a + bi is represented as a point
(a, b) in a coordinate plane. The horizontal axis of the
coordinate plane is called the real axis. The vertical axis is
called the imaginary axis. The coordinate system is called
the complex plane.
• When we represent a complex
number as a point in the complex
plane, we say that we are
plotting the complex number.

10. Example: Plotting Complex Numbers
•Plot the complex number in the complex plane:
z = 2 + 3i
z a bi
 
2 3
z i
 
2, 3
a b
 
We plot the point
(a, b) = (2, 3).
2 3
z i
 

11. Example: Plotting Complex Numbers
•Plot the complex number in the complex plane:
z = –3 – 5i
z a bi
 
3 5
z i
  
3, 5
a b
   
We plot the point
(a, b) = (–3, –5).
3 5
z i
  

12. Example: Plotting Complex Numbers
•Plot the complex number in the complex plane:
z = –4
z a bi
 
4 0
z i
  
4, 0
a b
  
We plot the point
(a, b) = (–4, 0).
4 0
z i
  

13. Example: Plotting Complex Numbers
•Plot the complex number in the complex plane:
z = –i
z a bi
 
0
z i
 
0, 1
a b
  
We plot the point
(a, b) = (0, –1).
0
z i
 

19. Polar Form of a Complex Number
•A complex number in the form z = x+ iy is said
to be in rectangular form.
•The expression is called
the polar form of a complex number.
(cos sin )
z r i
 
 

22. Example1: Finding the Modulus of a
Complex Number
5 12
z i
 
2 2
.
z a bi a b
   
2 2
5 12 5 12
z i
    25 144
  169
 13


23. Example2: Finding the Absolute Value
of a Complex Number
2 3
z i
 
2 2
.
z a bi a b
   
2 2
2 3 2 ( 3)
z i
     4 9
  13


26. Example: Writing a Complex Number
in Polar Form
•write the number in polar form: 1 3
z i
  
z a bi
 
1 3
z i
  
1, 3
a b
   
1 3
z i
  

27. Example: Writing a Complex Number
in Polar Form
1 3
z i
  
2 2
r a b
 
 
2
2
( 1) 3
   
1 3 4 2
   
tan
b
a
 
3
3
1

 

4
3

 

28. Example: Writing a Complex Number
in Polar Form
1 3
z i
  
The polar form of
is
1 3
z i
  
4
2,
3
r


 
(cos sin )
z r i
 
 
4 4
2 cos sin .
3 3
z i
 
 
 
 
 