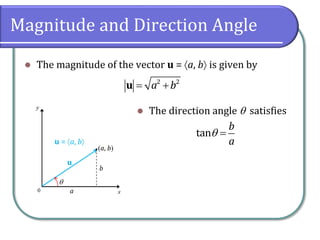
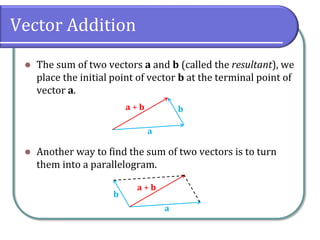
This document defines vectors and vector operations. It explains that a vector has both magnitude and direction, and can be represented by a directed line segment. The document covers finding the magnitude and direction angle of a vector, calculating the horizontal and vertical components, adding vectors using parallelograms, finding the magnitude of a resultant vector, and performing vector operations like addition, scalar multiplication, and subtraction. An example problem solves for the force needed to keep a car parked on an inclined surface using vector concepts.

1. 8.3 Vectors
Chapter 8 Applications of Trigonometry

2. Concepts and Objectives
 Vectors and Vector Operations
 Find the magnitude and direction angle for a vector.
 Find the horizontal and vertical components of a
vector.
 Find the magnitude of a resultant.
 Perform vector operations.
 Use vectors to solve problems.

3. Vectors – Vocabulary
 Magnitude is a word used to describe the size of
something, such as 35 lb or 100 mph.
 A vector quantity is a quantity that has both magnitude
and direction. For example, 60 mph east represents a
vector quantity.
 A vector quantity is often represented with a directed
line segment called a vector.
 The length of the vector represents the magnitude of
the vector quantity.
 The direction of the vector represents the direction of
the vector quantity.

4. Vectors
 In a coordinate plane, a vector with its endpoint at the
point a, b is written a, b, so
u = a, b
 The numbers a and b are the
horizontal and vertical components
of the vector.
 The positive angle  between the
x-axis and the vector is the
direction angle for the vector.a
b
a, b
u
u = a, b


5. Magnitude and Direction Angle
 The magnitude of the vector u = a, b is given by
 The direction angle  satisfies
a
b
a, b
u
u = a, b

2 2
a b u
tan
b
a


6. Magnitude and Direction Angle
 Example: Find the magnitude and direction angle for
u = ‒5, 4.

7. Magnitude and Direction Angle
 Example: Find the magnitude and direction angle for
u = ‒5, 4.
Magnitude:
Direction angle:
   
2 2
5 4u
 41 6.403


4
tan
5

1 4
tan
5
  
  
 

38.7    141.3
Direction angles are
always positive!
The vector is in
QII, so  must be
between 90° and
180°.

8. Magnitude and Direction Angle
 Example: Find the magnitude and direction angle for
u = ‒5, 4.
Magnitude:
Direction angle:
41u
141.3 

9. Horizontal & Vertical Components
 The horizontal and vertical components, respectively, of
a vector u having magnitude and direction angle  are
given by
u
cosa u  sinb  u 

10. Horizontal & Vertical Components
 Example: Vector v has magnitude 14.5 and direction
angle 220°. Find the horizontal and vertical
components.

11. Horizontal & Vertical Components
 Example: Vector v has magnitude 14.5 and direction
angle 220°. Find the horizontal and vertical
components.
14.5cos220a 
11.1 
14.5sin220b 
9.3 
11.1, 9.3 

12. Vector Addition
 The sum of two vectors a and b (called the resultant), we
place the initial point of vector b at the terminal point of
vector a.
 Another way to find the sum of two vectors is to turn
them into a parallelogram.
a
ba + b
a
b
a + b

13. Vector Addition
 Recall that a parallelogram is a quadrilateral whose
 Opposite sides are parallel
 Opposite sides are congruent
 Opposite angles are congruent
 Consecutive angles are supplementary

14. Magnitude of a Resultant
 Example: Two forces of 32 and 48 newtons act on a
point in the plane. If the angle between the forces is 76°,
find the magnitude of the resultant vector.
32 N
48 N
76°

15. Magnitude of a Resultant
 Example: Two forces of 32 and 48 newtons act on a
point in the plane. If the angle between the forces is 76°,
find the magnitude of the resultant vector.
32 N
48 N
76° 104°
48 N
  2 2 2
32 48 2 32 48 cos104   v
4071.18
64 Nv

16. Vector Operations
 For any real numbers a, b, c, d, and k:
, , ,a b c d a c b d   
, ,k a b ka kb

17. Vector Applications
 Example: Find the force required to keep a 2500-lb car
parked on a hill that makes a 12° angle with the
horizontal.
12°

18. Vector Applications
 Example: Find the force required to keep a 2500-lb car
parked on a hill that makes a 12° angle with the
horizontal.
The gravity vector is the sum of f,
the force with which the weight
pushes against the ramp, and ‒x.
12°
2500
Gravity always
points straight
down.
x
x
f

19. Vector Applications
 Example: Find the force required to keep a 2500-lb car
parked on a hill that makes a 12° angle with the
horizontal.
The gravity vector creates a
similar right triangle that we
can use trig to solve:12°
2500
12°
x
x
f
sin12
2500
 
x
2500sin12 x
520 lb

20. Vector Operations
 Example: Let u = 6, ‒3 and v = ‒14, 8. Find the
following: (a) u + v, (b) ‒2u, (c) 5u – 2v.

21. Vector Operations
 Example: Let u = 6, ‒3 and v = ‒14, 8. Find the
following: (a) u + v, (b) ‒2u, (c) 5u – 2v.
(a) u + v = 6 – 14, ‒3 + 8
(b) ‒2u = ‒26, ‒3
(c) 5u – 2v = 56, ‒3 – 2‒14, 8
= 30, ‒15 ‒ ‒28, 16
= 58, ‒31
= ‒8, 5
= ‒12, 6

22. Classwork
 College Algebra
 Page 770: 20-28 (even); page 756: 40, 42, 48-52, 60;
page 747: 76-84 (even)