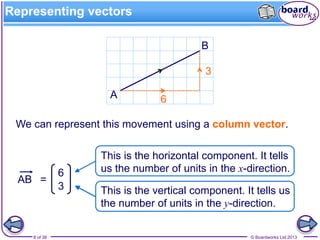
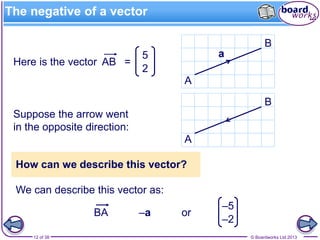
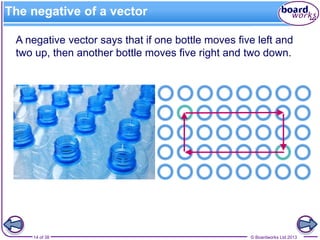
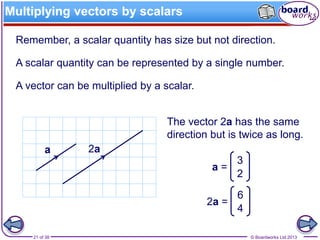
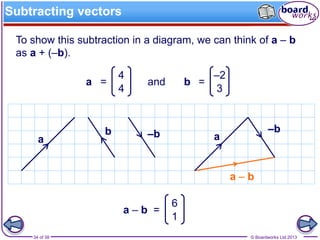
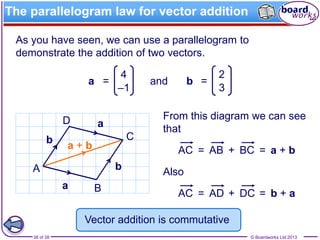
The document explains the concepts of vectors and scalars, emphasizing that vectors have both magnitude and direction while scalars have only magnitude. It covers representation, addition, subtraction, and multiplication of vectors, along with examples of equal vectors, negative vectors, and unit vectors. Additionally, it illustrates practical applications of these concepts in real-life situations such as meteorology and navigation.