The definite integral is used to find the area of a region bounded by curves. Specifically, the area A between two curves f(x) and g(x) on the interval [a,b] is given by the definite integral: A = ∫ab [f(x) - g(x)] dx To calculate the area, one finds the points where the two curves intersect, then evaluates the integral of the top curve minus the bottom curve between the bounds a and b. For examples where the region is bounded along the y-axis, the integral is evaluated with respect to y. The definite integral provides a way to precisely calculate the area of a region defined by curves.

1. What’s the definite integral used for?

2. f
g
Area of region
between f and g
f
=
=
g
-
Area of region
under f(x)
b
a
a
g
b
b
(x x
∫[f(x)−g )]d =∫ f ( x)dx
f
−
Area of region
under g(x)
∫ g ( x)dx
a

3. 7.1 Areas Between Curves
To find the area:
• divide the area into n strips of
equal width
• approximate the ith strip by a
rectangle with base Δx and height
f(xi) – g(xi).
• the sum of the rectangle areas is a
good approximation
• the approximation is getting better
as n→∞.
y = f(x)
y = g(x)
The area A of the region bounded by the curves y=f(x), y=g(x), and
the lines x=a, x=b, where f and g are continuous and f(x) ≥ g(x) for
all x in [a,b], is
b
A = ∫ [ f ( x) − g ( x)]dx
a

4. To find the area between 2 curves
(along the x-axis)
• Sketch a graph (if you can)
• Draw a representative rectangle to determine
the upper and lower curves.
• Use the formula:
Area = Top curve – bottom curve
b
A ∫[f(x (x ] x =
=
)−g ) d
a

5. Ex. Find the area of the region bounded by the graphs
of f(x) = x2 + 2, g(x) = -x, x = 0, and x = 1 .
Area = Top curve – bottom curve
b
A ∫[f(x (x ] x =
=
)−g ) d
a
1
2
(x +2 ( x ] x=
∫[ )− − ) d
0
1
1 1
17
x

x
 + + 2 x = 3 + 2 + 2 = 6
3 2
0
3
2

6. Find the area of the region bounded by the graphs of
f(x) = 2 – x2 and g(x) = x
First, set f(x) = g(x) to
find their points of
intersection.
2 – x2 = x
0 = x2 + x - 2
0 = (x + 2)(x – 1)
x = -2 and x = 1
∫[
(
1
−
2
) ]
9
2−x −x d fnInt(2 – x – x, x, -2, 1) =
x=
2
2
2

7. Find the area of the region between the graphs of
f(x) = 3x3 – x2 – 10x and g(x) = -x2 + 2x
Again, set f(x) = g(x)
to find their points of
intersection.
3x3 – x2 – 10x = -x2 + 2x
3x3 – 12x = 0
3x(x2 – 4) = 0
x = 0 , -2 , 2
Note that the two graphs switch at the origin.

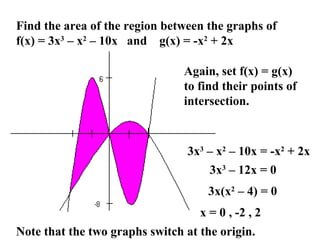
8. Now, set up the two integrals and solve.
0
2
−
2
0
)− ( ) d
g )− ) d
∫[f(x gx] x+∫[ (x f (x] x
0
2
x 1 x x+ −x 1 x x=
∫(3 − 2 )d ∫( 3 + 2 )d
3
−
2
3
0
= 24

9. x2
A = ∫ [(top curve) − (bottom curve)] dx
x1
y2
A = ∫ [(right curve) − (le f t curve)] dy
y1

10. 1. Find the area of the region bounded by the graphs
of y = 6 + 3 x − x 2 , y = 2 x − 9 , x = -2 , and x = 2.
2.Find the area of the region bounded by the graphs
y = x 2 − 5 , and y = 1 − x .
of

11. Find the area of the region bounded by the graphs
of x = 3 – y2 and y = x - 1

12. When you integrate with respect to Y:
•Your functions must all be in terms of y
•Your variable of integration changes to “dy”
•The formula for Area between curves becomes:
b
A = ∫ [(right curve) − (le f t curve)] dy
a

13. Find the area of the region bounded by the graphs
of x = 3 – y2 and y = x - 1
Area = Right - Left
1
A ∫[ −y )− 1] y
= (
3
(y+ ) d
2
−
2
9
=
2

14. Find the area of the region bounded by the graphs
of x = y2 and y = x - 2