Embed presentation
Downloaded 29 times


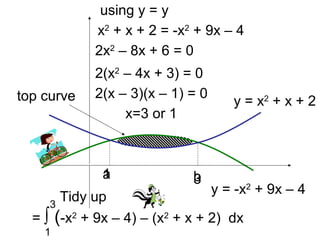
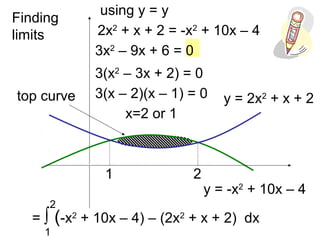
![Tidying Up
= ∫ (-x2
+ 9x – 4) – (x2
+ x + 2) dx
1
3
= ∫ (-x2
+ 9x – 4 – x2
– x – 2) dx
1
3
1
3
= ∫ (-2x2
+ 8x – 6) dx
= [-2
/3x3
+ 4x2
– 6x]
1
3
= -2
/3(3)3
+ 4(3)2
– 6(3) – [-2
/3(1)3
+ 4(1)2
– 6(1)]
= 0 – (-21
/3)
= 21
/3 units2](https://image.slidesharecdn.com/area-between-curves-160218000615/85/Area-between-curves-6-320.jpg)

![Find area enclosed by y = x2
and y = 3x – 2
y = y
x2
= 3x – 2
x2
– 3x + 2 = 0
(x – 2)(x – 1) = 0
x = 2 or x = 1
y = 3x – 2
2
= ∫ (3x – 2 – x2
) dx
y = x2
1
2
1
= [3
/2x2
– 2x – 1
/3x3
]
1
2
= 3
/2(2)2
– 2(2) – 1
/3(2)3
– [3
/2(1)2
– 2(1) – 1
/3(1)3
]
= -2
/3 – (-5
/6)
= 1
/6 units2
Key Question](https://image.slidesharecdn.com/area-between-curves-160218000615/85/Area-between-curves-10-320.jpg)
![Find area enclosed by y = 2x and
y = 4x – x2
y = y
2x = 4x – x2
x2
– 2x = 0
x(x – 2) = 0
x = 0 or x = 2
y = 2x
2
= ∫ (4x – x2
– 2x) dx
y = 4x – x2
0
2
= ∫ (2x – x2
) dx
0
2
= [x2
– 1
/3x3
]
0
2
= 22
– 1
/3(2)3
– 0
= 11
/3 units2](https://image.slidesharecdn.com/area-between-curves-160218000615/85/Area-between-curves-11-320.jpg)
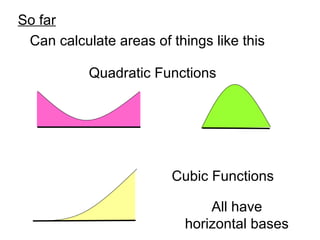
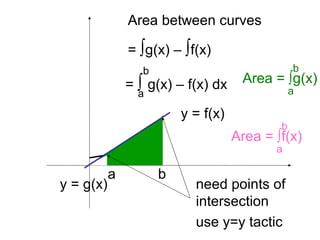
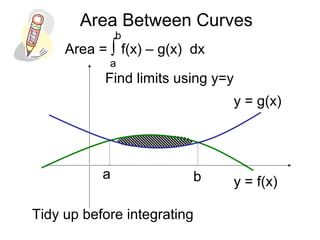
The document provides steps to calculate the area between two curves by finding the intersection points using "y=y" and then integrating between those points. It works through multiple examples of finding the area between various curve combinations, including quadratic, cubic, and linear functions. The key steps are finding the intersection points using "y=y", setting up the integral as the top curve minus the bottom curve, and integrating between the bounds found from the intersection points.





![Tidying Up
= ∫ (-x2
+ 9x – 4) – (x2
+ x + 2) dx
1
3
= ∫ (-x2
+ 9x – 4 – x2
– x – 2) dx
1
3
1
3
= ∫ (-2x2
+ 8x – 6) dx
= [-2
/3x3
+ 4x2
– 6x]
1
3
= -2
/3(3)3
+ 4(3)2
– 6(3) – [-2
/3(1)3
+ 4(1)2
– 6(1)]
= 0 – (-21
/3)
= 21
/3 units2](https://image.slidesharecdn.com/area-between-curves-160218000615/85/Area-between-curves-6-320.jpg)



![Find area enclosed by y = x2
and y = 3x – 2
y = y
x2
= 3x – 2
x2
– 3x + 2 = 0
(x – 2)(x – 1) = 0
x = 2 or x = 1
y = 3x – 2
2
= ∫ (3x – 2 – x2
) dx
y = x2
1
2
1
= [3
/2x2
– 2x – 1
/3x3
]
1
2
= 3
/2(2)2
– 2(2) – 1
/3(2)3
– [3
/2(1)2
– 2(1) – 1
/3(1)3
]
= -2
/3 – (-5
/6)
= 1
/6 units2
Key Question](https://image.slidesharecdn.com/area-between-curves-160218000615/85/Area-between-curves-10-320.jpg)
![Find area enclosed by y = 2x and
y = 4x – x2
y = y
2x = 4x – x2
x2
– 2x = 0
x(x – 2) = 0
x = 0 or x = 2
y = 2x
2
= ∫ (4x – x2
– 2x) dx
y = 4x – x2
0
2
= ∫ (2x – x2
) dx
0
2
= [x2
– 1
/3x3
]
0
2
= 22
– 1
/3(2)3
– 0
= 11
/3 units2](https://image.slidesharecdn.com/area-between-curves-160218000615/85/Area-between-curves-11-320.jpg)