Downloaded 247 times
Uploaded byFarhatunisa
7. analisis deret berkala 1
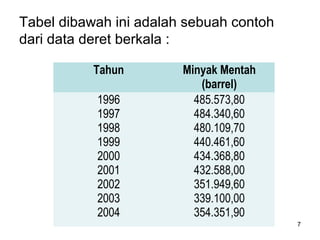
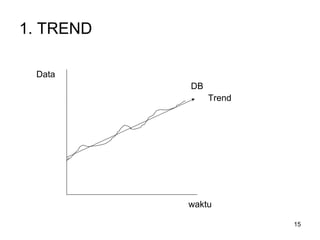
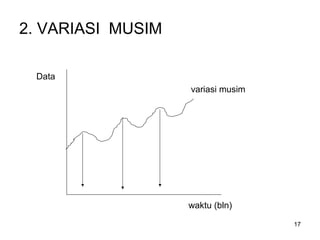
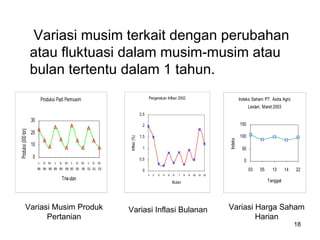
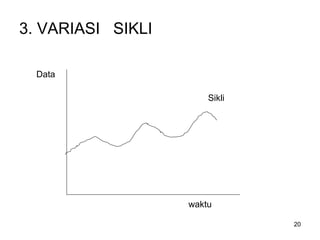
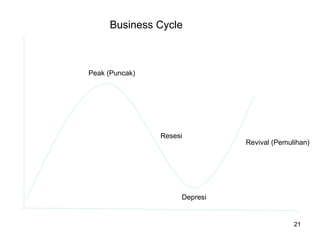
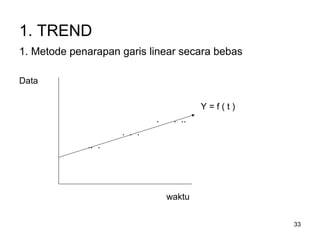
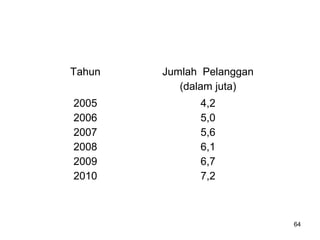
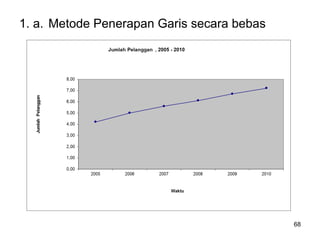
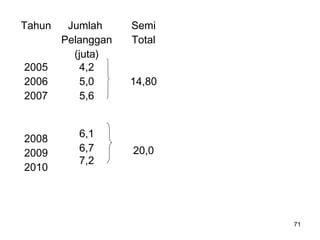
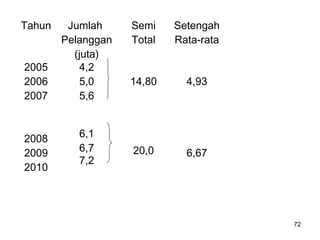
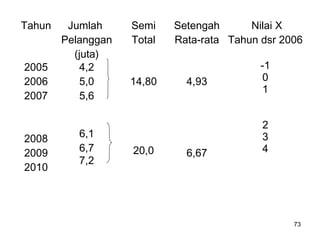
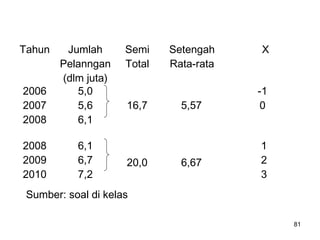
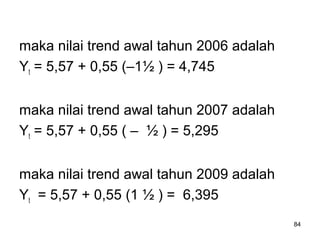
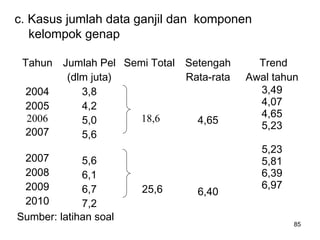
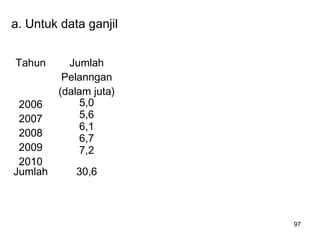
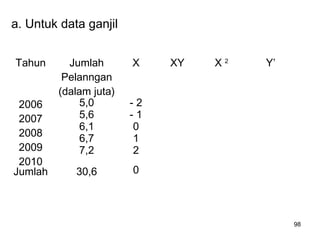
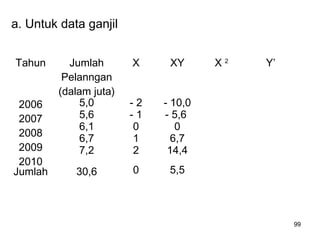
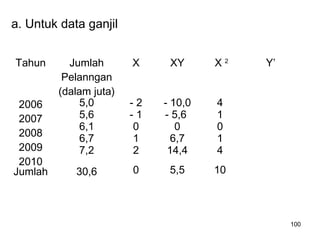
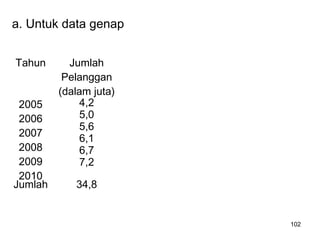
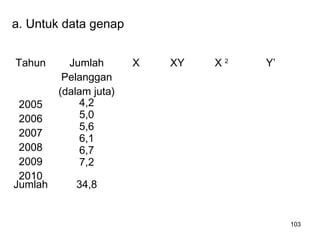
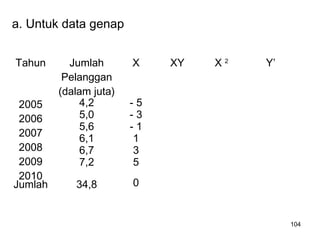
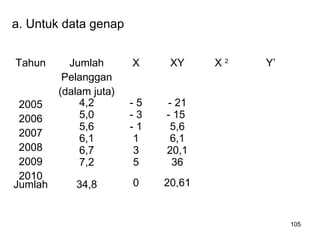
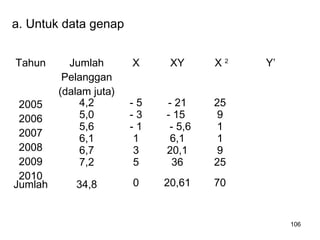
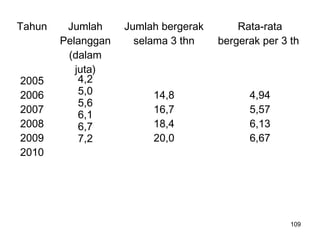
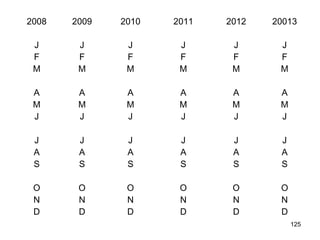
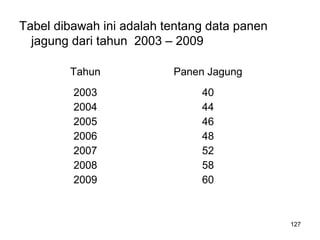
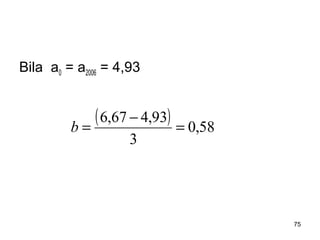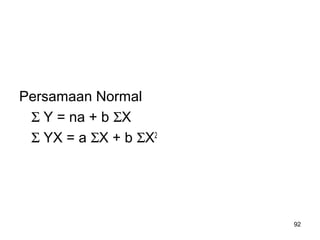Analisa deret berkala digunakan untuk menganalisis pola data masa lalu agar dapat memprediksi masa depan. Terdapat empat komponen yang mempengaruhi pola data yaitu tren jangka panjang, variasi musiman, siklus, dan variasi acak. Tren menunjukkan arah pergerakan data dalam jangka panjang, variasi musiman mempengaruhi fluktuasi tahunan, siklus mempengaruhi pergerakan dalam siklus jangka menengah,
More Related Content
Similar to 7. analisis deret berkala 1
![Modul Ajar KBC Akidah Akhlak Kelas 5 MI [MODULKELAS.COM]](https://cdn.slidesharecdn.com/ss_thumbnails/modulajarkbcakidahakhlakkelas5mimodulkelas-260205160818-304c5d00-thumbnail.jpg?width=640&height=640&fit=bounds)
7. analisis deret berkala 1
- 1.
- 2. • Peramalan adalahsebuah alat utama untuk membuat keputusan dari setiap proses (pekerjaan) yang dibuat. 2
- 3. • Analisa inidigunakan untuk berbagai macam keperluan, dari menentukan bahan yang diperlukan untuk memproduksi di toko makanan rumahan sampai meramalkan hasil penjualan tahunan dari PT. Krakatau Steel. 3
- 4. • Kualitas daricara peramalan dapat menguatkan informasi yang dapat digali dengan menggunakan data masa lalu. 4
- 5. • Analisa DeretBerkala adalah sebuah metoda kuantitatif yang dapat kita gunakan untuk menentukan pola dari data yang terkumpul beberapa waktu dimasa lalu. 5
- 6. 6 • Seorang pimpinanharus dapat meramalkan bagaimana volume penjualan tahun depan, bagaimana keadaan perniagaan bergerak dari bulan ke bulan atau dari tahun ke tahun. Misalnya berapa banyak barang harus diproduksi untuk tahun depan, tentang harga bahan-bahan baku, harga barang-barang jadi yang dihasilkan, situasi pasaran barang, keperluan pegawai dan lain sebaginya.
- 7. Tabel dibawah iniadalah sebuah contoh dari data deret berkala : Tahun Minyak Mentah (barrel) 1996 1997 1998 1999 2000 2001 2002 2003 2004 485.573,80 484.340,60 480.109,70 440.461,60 434.368,80 432.588,00 351.949,60 339.100,00 354.351,90 7
- 8. 8 • DefinisiDefinisi:: adalahsekumpulan hasil pengamatan terhadap suatu variabel yang diatur dan didapat menurut kronologis, biasanya dalam interval waktu yang sama. • Contoh lainContoh lain: penjualan mingguan barang x, produksi bulanan di seluruh industri, produksi tahunan biji besi di Indonesia dlsb.
- 9. Analisa deret berkaladigunakan untuk menemukan pola perubahan dalam bentuk informasi statistic sampai melewati jarak waktu yang ada. 9
- 10. Juga akan kitarancang pola ini untuk memperoleh sebuah peramalan untuk masa yang akan datang. 10
- 11. 11 • Umumnya penelitimerasa puas jika 85% atau 90% hasil ramalan terjadi, walaupun ia menginginkan lebih tinggi. Yang jelas tidak akan/jarang tercapai hasil ramalan tepat 100%.
- 12. 12 • Data deretwaktu dipengaruhi oleh berbagai faktor, misalnya: bencana alam, selera konsumen, manusia, musim, kebiasaan dlsb. Karena banyaknya faktor- faktor yang mempengaruhi, maka analisa sangat berat dan praktis tidak mungkin untuk menjelaskan pengaruh setiap faktor satu demi satu.
- 13. 13 • Analisa klasikbiasanya hanya membahas pemecahan data deret waktu menjadi 4 faktor yang seakan-akan independen satu dengan yang lainnya dan dianggap penga-ruhnya dapat menjelaskan keseluruhan, yaitu:
- 14. 14 1. Gerakan yangberjangka panjang, lam- ban berkecenderungan menuju ke satu arah, naik atau turun disebut Trend Se- kuler. • Nilai dari variable cenderung untuk naik atau turun selama periode yang panjang • (Trend sekuler, Long term Variation , TS ).
- 15.
- 16. 16 2. Ayunan sekitartrend yang bersifat musi- man serta kurang lebih teratur, disebut Variasi Musim. • Variasi musim memiliki pola perubahan dalam satu tahun dan cenderung berulang setiap tahunnya. • (Variasi Musim , Seasonal Movement ,Vm).
- 17. 17 2. VARIASI MUSIM Data variasimusim waktu (bln)
- 18. 18 Variasi musim terkaitdengan perubahan atau fluktuasi dalam musim-musim atau bulan tertentu dalam 1 tahun. Produksi Padi Permusim 0 10 20 30 I- 98 II- 98 III- 98 I- 99 II- 99 III- 99 I- 00 II- 00 III- 00 I- 01 II- 01 III- 03 Triwulan Produksi(000ton) Pergerakan Inflasi 2002 0 0,5 1 1,5 2 2,5 1 2 3 4 5 6 7 8 9 10 11 12 Bulan Inflasi(%) Indeks Saham PT. Astra Agro Lestari, Maret 2003 0 50 100 150 03 05 13 14 22 Tanggal Indeks Variasi Musim Produk Pertanian Variasi Inflasi Bulanan Variasi Harga Saham Harian
- 19. 19 3. Berjangka lebihpanjang dan agak lebih tidak teratur, disebut Variasi Sikli • Perubahan dari siklis agak lebih tidak teratur. • (Variasi Sikli, Konjungtur, Cyclical Variation, VS).
- 20.
- 21.
- 22. 22 4. Gerakan yangtidak teratur sama sekali dan yang terkenal dengan nama Variasi Random atau Residu • Dalam beberapa situasi, nilai dari variasi sama sekali tidak dapat diramalkan, perubahannya random. • (Irregular , Residu, Komponen tidak beraturan , R ).
- 23. 23 4. VARIASI RANDOM •Variasi Random (Residu), sifatnya tidak teratur dan sukar dikuasai umumnya gera- kan ini disebabkan oleh faktor kebetulan, misalnya disebabkan oleh peperangan, banjir, gempa bumi, perubahan politik, pe- mogokan dsb. Akibatnya dapat mempenga- ruhi kegiatan perdagangan, perindustrian dll sehingga gerak ini sukar dilukiskan dalam suatu model.
- 24. 24 Hubungan antara ke4 komponen ini berbeda-beda, beberapa ahli sampai saat ini belum sependapat apakah hubungan- nya multiplikatif atau additif atau kombina- si lainnya dan mungkin ada komponen lain.
- 25. 25 1. Model Multiplikatif/Model Perkalian Db = Ts . Vs . Vm . R Hasil bulanan dianggap sebagai produk dari ke 4 faktor. Untuk data tahunan gerak musiman tidak tercerminkan, jadi Db = Ts . Vs . R Jika Ts . Vs .R/ Ts = Vs . R → pengaruh siklis dan residu. Jika digunakan metoda rata-rata bebe- rapa Vs . R akan dihasilkan gerak Vs
- 26. 26 2. Model Aditif/Model Pertambahan Db = Ts + Vs + Vm + R Data deret waktu merupakan hasil pen- jumlahan pengaruh Ts , Vs , Vm dan R • Dan untuk analisa selanjutnya kita mela- kukan asumsi bahwa deret berkala meru- pakan hasil perkalian dari komponen- komponennya.
- 27. I. TREND SEKULER •Trend Sekuler menunjukkan gerakan berjangka panjang. Satu cara untuk menjelaskan komponen trend adalah dengan menggabungkan sekumpulan titik- titik dalam sebuah grafik. 27
- 28. Mengapa harus mempelajari Trend Terdapat3 alasan mengapa perlu mempelajari trend sekuler 28
- 29. 1. Mempelajari trendsekuler membuat kita dapat menjelaskan pola dari kejadian masa lalu. 29
- 30. 2. Mempelajari trendsekuler membuat kita dapat mencanangkan pola masa lalu , atau trendnya untuk waktu yang akan datang. 30
- 31. 3. Dalam beberapasituasi, mempelajari trend sekuler dari deret berkala membuat kita dapat melenyapkan komponen trend dari data berkala. 31
- 32. 32 1. TREND Tehnik menghitungserta penerapan garis trend pada gerakan sekuler 1. Metode penarapan garis linear secara bebas 2. Metode Setengah Rata-rata (Semi Average Method) 3. Metode penerapan garis trend secara matematis 4. Metode Kuadrat Minimum/Kuadrat Terkecil (Least Square Method) 5. Metode Rata-rata Bergerak/Rata-rata Berpindah (Moving Average Method)
- 33. 33 1. TREND 1. Metodepenarapan garis linear secara bebas Data Y = f ( t ) . . .. . . . .. . waktu
- 34. 34 1. TREND 2. MetodeSetengah Rata-rata (Semi Average Method) Yt = a0 + b t Yt adalah nilai trend pada periode tertentu a0 adalah nilai trend pada periode dasar b adalah pertambahan/ pengurangan trend tahunan secara rata-rata t adalah jumlah unit tahun yang dihitung dari periode dasar
- 35. 35 1. TREND Untuk datayang ganjil • Jumlah deret berkala dikelompokkan menjadi dua bagian yang sama dengan cara memasukkan tahun dan nilai terte- ngah kedalam tiap kelompok. • Jumlah deret berkala dikelompokkan menjadi dua bagian yang sama dengan jalan menghilangkan tahun dan nilai tertengah.
- 36. 36 1. TREND 3. Metodepenerapan garis trend secara Matematis. Persamaan Yt = a0 + b t Persamaan Normal Σ Y = na + b Σ X Σ YX = a Σ X + b Σ X2
- 37. 37 1. TREND 4. MetodeKuadrat terkecil (Least Square Method) Persamaannya : Yt = a0 + b t atau Y’ = a + b x dann Y a ∑= ∑ ∑= 2 X XY b
- 38. 38 1. TREND Ekstrapolasi • Secarateknis ekstrapolsi berarti menaksir nilai yang sebetulnya terletak diluar batas nilai-nilai yang digunakan sebagi dasar perumusan persamaan trend pada umumnya.
- 39. 39 1. TREND Meskipun ekstrapolasiberguna sekali bagi pemimpin perusahaan, tetapi sifatnya sangat spekulatif dan harus diberi inter- pretasi secara hati-hati. Karena selama kurun waktu penaksiran pertumbuhan ekonomi daerah, perkembangan pasar, perubahan pola konsumsi, kegoncangan politik dlsb dapat mempengaruhi per- kembangan fenomena ekonomi dimasa yang akan datang.
- 40. 40 1. TREND 5. MetodeRata-rata Bergerak (Moving Average Method) • Didalam cara ini kita tidak mendapatkan persamaan trendnya akan tetapi kita ha- nya dapat menentukan nilai-nilai trendnya. • Metode ini sering digunakan untuk meng- ratakan deret berkala yang bergelombang
- 41. 41 1. TREND 5. MetodeRata-rata Bergerak (Moving Average Method) • Menghitungnya dari rata-rata bergerak beberapa tahun secara berturut-turut atas dasar jumlah tahun yang tertentu. Metode ini tidak memberi ketentuan ten- tang jumlah tahun yang harus digunakan sebagai dasar pengrata-rataan. Makin banyak jumlah tahun yang digunakan makin rata bentuk kurva yang diperoleh dan makin intensif kita mengisolasikan fluktuasi Musim (Vm), Residu ( R ) dan Sikli (Vs).
- 42. 42 1. TREND 5. MetodeRata-rata Bergerak (Moving Average Method) • Metode ini dibedakan atas dasar jumlah tahun yang digunakan untuk mencari rata-ratanya. • Bila kita gunakan 3 tahun sebagai dasar rata-rata bergerak, tehnik tersebut dina- makan rata-rata bergerak per 3 tahun
- 43. 43 2. VARIASI MUSIM •Fluktuasi sekitar trend yang berulang secara teratur tiap-tiap tahun disebut variasi musim (seasonal variation). Variasi ini dapat disebabkan oleh faktor alami maupun institusional dan membawa pengaruh terhadap pola itu sendiri.
- 44. 44 2. VARIASI MUSIM •Pola tersebut sangat berguna bagi perencanaan produksi, penggunaan tenaga kerja dalam jangka pendek. Selain itu pola Vm dapat digunakan bagi dasar kebijakan pimpinan perusahaan dalam mengatur diversifikasi produk dan kegiatan produksi.
- 45. 45 2. VARIASI MUSIM •Per definisi : Db = Ts . Vs . Vm . R • Untuk memperoleh Vm , maka harus mengisolasikan Ts , Vs dan R dari Db. Pengisolasian tersebut akan menghasil- kan Vm yang dapat digunakan sebagai dasar penyusunan indeks musim (seasonal indices).
- 46. 46 2. VARIASI MUSIM •Vm dari data bulanan terdiri dari 12 ang- ka indeks yang menggambarkan gera- kan musim tiap-tiap bulan dalam bentuk indeks. • Pembentukan indeks tersebut hendak- nya menggunakan rata-rata bulanan da- ri beberapa tahun agar dapat menghi- langkan fluktuasi Ts dan Vs .
- 47. 47 2. VARIASI MUSIM •Indeks yang diperoleh merupakan indeks yang menggambarkan gerakan rata-rata tiap bulan sebegai persentase dari gera-kan rata-rata semua bulan yang diikut sertakan dalam penyusunan indeks.
- 48. 48 2. VARIASI MUSIM Ada3 cara untuk memperoleh Vm yaitu: 1. Metode rata-rata sederhana (cara % rata-rata) 2. Metode % dari trend (falkners method/ cara perbandingan dari trend) 3. Metode rasio terhadap rata-rata bergerak (cara % rata-rata bergerak atau cara perbandingan terhadap rata-rata bergerak).
- 49. 49 2. VARIASI MUSIM Ada3 cara untuk memperoleh Vm yaitu: 1. Metode rata-rata sederhana (cara % rata-rata) • Secara sederhana metode ini bertujuan guna menghilangkan gerakan Vs dan R, baru kemudian menghilangkan Ts untuk memperoleh Vm .
- 50. 50 2. VARIASI MUSIM Ada3 cara untuk memperoleh Vm yaitu: 1. Metode rata-rata sederhana (cara % rata-rata) Rumusnya: n adalah jumlah tahun ( ) s mss T n RVVT − ...
- 51. 51 2. VARIASI MUSIM Ada3 cara untuk memperoleh Vm yaitu: 2. Metode % dari trend (falkners method/ cara perbandingan dari trend)
- 52. 52 2. VARIASI MUSIM Ada3 cara untuk memperoleh Vm yaitu: 3. Metode rasio terhadap rata-rata bergerak (cara % rata-rata bergerak atau cara perbandingan terhadap rata-rata bergerak). • Hingga saat ini cara ini merupakan cara yang dianggap memuaskan dibandingkan dengan ketiga cara lainnya.
- 53. 53 2. VARIASI MUSIM Ada3 cara untuk memperoleh Vm yaitu: 3. Metode rasio terhadap rata-rata bergerak (cara % rata-rata bergerak atau cara perbandingan terhadap rata-rata bergerak). • Rata-rata bergerak untuk data bulanan, dihitung jumlah rata-rata bergerak 12 bulan. • Rata-rata bergerak untuk data kuartalan, dihitung jumlah rata-rata bergerak 4 bulanan.
- 54. 54 3. GERAKAN SIKLIDAN RESIDU • Pengertian sikli sebetulnya variasi dari Db yang meliputi periode lebih dari 1 tahun. Pola sikli sedemikian itu paling sukar diter- ka. Lama dan amplitudo sikli tidak pernah sama. Rangkaian ayunannya memang berulang kali, tetapi sifatnya tidak pernah periodik. Lama Vs bervariasi dari periode yang meliputi beberapa tahun hingga periode yang meliputi 10 bahkan 12 tahun.
- 55. 55 3. GERAKAN SIKLIDAN RESIDU • R atau variasi random merupakan jenis fluktuasi yang disebabkan oleh faktor- faktor random atau sebab-sebab khusus yang sporadis. Variasi ini sukar ditaksir meskipun gerakannya menimbulkan vari- asi dari periode ke periode. R acapkali dapat dianggap hanya sebagai bagian dari Vs dan Vm.
- 56. 56 3. GERAKAN SIKLIDAN RESIDU Pengukuran Vm. Db umumnya terdiri dari dua komponen yaitu Ts dan Vs Bila data tahunan maka Vm tidak akan nampak R merupakan gerakan yang tidak reguler yg memiliki pengaruh yang bersifat jangka pendek jika ditinjau dari sudut periode ta- hunan sehingga pengaruhnya bertendensi saling meniadakan selama setahun.
- 57. 57 3. GERAKAN SIKLIDAN RESIDU Pengukuran Vs. Jika ditinjau dari data tahunan, nilai Ts da- pat dianggap sebagai normal, yaitu per- tumbuhan tahunan yang normal jika tidak terdapat pengaruh Vs. Dengan perkataan lain, Vs dapat dianggap sebagai deviasi dari Ts . Sehingga pemisahannya adalah dengan jalan membagi Db dengan Ts hasilnya relatif sikli (Cyclical Relatives).
- 58. 58 3. GERAKAN SIKLIDAN RESIDU % deviasi relatif sikli yaitu: 1001 × − s b T D
- 59. 59 3. GERAKAN SIKLIDAN RESIDU % deviasi residu sikli yaitu: 100× − s sb T TD
- 60. 60 3. GERAKAN SIKLIDAN RESIDU Cara menentukan gerakan Sikli (Vs). • Karena Vm untuk data tahunan tidak ada, persamaan Db = Ts .Vs . R jika persama- an tersebut kita bagi dengan Ts hasilnya adalah Vs . R • Untuk mengukur pengaruh gabungan dila- kukan pembagian antara nilai sebenarnya dengan nilai trend untuk tahun ybs. Hasilnya dinyatakan dalam %.
- 61. 61 3. GERAKAN SIKLIDAN RESIDU • Persen dari pada trend adalah: • Hasilnya dinyatakan sebagai % dari pada nilai trend. =× %100' Y Yi RV T RVT Y Y s s ssi . .. ' ==∴
- 62.
- 63. 63 A. Tabel dibawahini adalah tentang jumlah pelanggan salah satu alat komunikasi di Indonesia yaitu PT “XYZ” dari tahun 2005 – 2010
- 64. 64 Tahun Jumlah Pelanggan (dalamjuta) 2005 2006 2007 2008 2009 2010 4,2 5,0 5,6 6,1 6,7 7,2
- 65. Pertanyaannya : 1. Tentukanpersamaan trend dari pelanggan PT. “XYZ” dengan metode: a. Metode Penerapan Garis secara bebas b. Metode Setengah Rata – rata c. Metode Matematis d. Metode Kuadrat Terkecil e. Metode Rata – rata Bergerak 65
- 66. 2. Tentukan jumlahpelanggan PT ”XYZ” pada tahun 2014. 3. Rubahlah persamaan trendnya menjadi bulanan dgn thn dsr 2006 4. Rubahlah persamaan trend (1) menjadi - trend semesteran dengan waktu dasar semester I - trend triwulan dengan waktu dasar triwulan II - trend bulanan dengan waktu dasar 15 Juli 2004 66
- 67. 5. Lakukan peramalanutk tahun 2014 dari jawaban 4 67
- 68. 1. a. MetodePenerapan Garis secara bebas 68
- 69. 69 1.b. Metode SetengahRata-rata (Semi Average Method) a. Kasus jumlah data genap dan komponen kelompok ganjil
- 70.
- 71.
- 72.
- 73. 73 Tahun Jumlah Pelanggan (juta) Semi Total Setengah Rata-rata Nilai X Tahundsr 2006 2005 2006 2007 2008 2009 2010 4,2 5,0 5,6 6,1 6,7 7,2 14,80 20,0 4,93 6,67 -1 0 1 2 3 4
- 74. 74 4,93 adalah nilaitrend jumlah pelanggan Telkom periode dasar 30 Juni 2006 6,67 adalah nilai trend jumlah pelanggan Telkom periode dasar 30 Juni 2009
- 75. 75 Bila a0 =a2006 = 4,93 ( ) 58,0 3 93,467,6 = − =b
- 76. 76 Yt = 4,93+ 0,58 t Tahun dasar 30 Juni 2006 Unit t : 1 tahun Yt : jumlah pelanggan PT ”XYZ” per tahun Yt = 6,67 + 0,58 t Tahun dasar 30 Juni 2009 Unit t : 1 tahun Yt : jumlah pelanggan PT ”XYZ” per tahun
- 77. • 0.58 =rata2 peningkatan jumlah pelanggan “XYZ” pertahun selama 2005- 2010 • 4.93 = jumlah pelanggan pada tanggal 30 juni 2006 77
- 78. 78 maka nilai trendawal tahun 2006 adalah Yt = 4,93 + 0,58 ( – ½ ) = 4,64 maka nilai trend awal tahun 2009 adalah Yt = 4,93 + 0,58 (2 ½ ) = 6,38 Bila a0 = a2009 = 6,67 maka nilai trend awal tahun 2009 adalah Yt = 6,67 + 0,58(– ½ ) = 6,38
- 79. 79 1.b. Metode SetengahRata-rata (Semi Average Method) b. Kasus jumlah data ganjil dan komponen kelompok ganjil
- 80. 80 Untuk data yangganjil • Jumlah deret berkala dikelompokkan men- jadi dua bagian yang sama dengan jalan menghilangkan tahun dan nilai tertengah. • Jumlah deret berkala dikelompokkan men- jadi dua bagian yang sama dengan cara memasukkan tahun dan nilai tertengah kedalam tiap kelompok.
- 81.
- 82. 82 • 5,57 adalahnilai trend jumlah pelanggan PT. ”XYZ” periode dasar 30 Juni 2007 6,67 adalah nilai trend jumlah pelanggan PT. ”XYZ” periode dasar 30 Juni 2009
- 83. 83 • Bila a0= a2007 = 5,57 Maka persamaan trend 2007 adalah • Yt = 5,57 + 0,55 t Tahun dasar 30 Juni 2007 Unit t : 1 tahun Yt jumlah pelanggan PT. “XYZ” ( ) 55,0 2 57,567,6 = − =b
- 84. 84 maka nilai trendawal tahun 2006 adalah Yt = 5,57 + 0,55 (–1½ ) = 4,745 maka nilai trend awal tahun 2007 adalah Yt = 5,57 + 0,55 ( – ½ ) = 5,295 maka nilai trend awal tahun 2009 adalah Yt = 5,57 + 0,55 (1 ½ ) = 6,395
- 85. 85 c. Kasus jumlahdata ganjil dan komponen kelompok genap Tahun Jumlah Pel (dlm juta) Semi Total Setengah Rata-rata Trend Awal tahun 2004 2005 2006 2007 2007 2008 2009 2010 3,8 4,2 5,0 5,6 5,6 6,1 6,7 7,2 18,6 25,6 4,65 6,40 3,49 4,07 4,65 5,23 5,23 5,81 6,39 6,97 Sumber: latihan soal
- 86. 86 • Yt =4,65 + 0,58 t Tahun dasar 1 Jan 2006/ 31 Des 2005 Unit t : 1 tahun Yt : jumlah pelanggan dalam juta • Yt = 6,40 + 0,58 t Tahun dasar 1 Jan 2009/ 31 Des 2008 Unit t : 1 tahun Yt : jumlah pelanggan dalam juta
- 87. 87 1. TREND Metode penerapangaris trend secara matematis
- 88. 88 1.c. Metode penerapangaris trend secara Matematis. Persamaan Yt = a0 + b t Persamaan bagi nilai-nilai observasi dan nilai trend bagi garis linear adalah Σ Yt = Σ Yt‘= Σ ( a + bt) Yt adalah nilai deret berkala hasil obse- rvasi pada periode t Yt‘ adalah nilai trend yang telah dihitung pada periode t
- 89. 89 1.c. Metode penerapangaris trend secara Matematis. Persamaan Normal Σ Y = na + b ΣX Σ YX = a ΣX + b ΣX2
- 90.
- 91. 91 Tahun X PelangganXY X^2 2005 2006 2007 2008 2009 2010 0 1 2 3 4 5 4,2 5,0 5,6 6,1 6,7 7,2 0 5 11,2 18,3 26,8 36 0 1 4 9 16 25 Jumla h 15 34,8 97,30 55
- 92. 92 Persamaan Normal Σ Y= na + b ΣX Σ YX = a ΣX + b ΣX2
- 93. 93 34,8 = 6a + 15 b x 10 97,3 = 15 a + 55 b x 4 348 = 60 a + 150 b 389,2 = 60 a + 220 b − − 41,2 =− 70 b b = 0,5886
- 94. 94 34,8 = 6a + 15 (0.5886) 6 a = 25,971 a = 4,3285 Y ‘ = 4,3285 + 0,5886 t Tahun dasar 30 Juni 2005 Unit t : 1 tahun Yt : jumlah pelanggan per tahun
- 95. 95 1. TREND d. MetodeKuadrat Minimum/Kuadrat Terkecil (Least Square Method)
- 96. 96 1.d. Metode Kuadratterkecil (Least Square Method) Y’ = a + b x dan n Y a ∑= ∑ ∑= 2 X XY b
- 97. 97 a. Untuk dataganjil Tahun Jumlah Pelanngan (dalam juta) 2006 2007 2008 2009 2010 5,0 5,6 6,1 6,7 7,2 Jumlah 30,6
- 98. 98 a. Untuk dataganjil Tahun Jumlah Pelanngan (dalam juta) X XY X 2 Y’ 2006 2007 2008 2009 2010 5,0 5,6 6,1 6,7 7,2 - 2 - 1 0 1 2 Jumlah 30,6 0
- 99. 99 a. Untuk dataganjil Tahun Jumlah Pelanngan (dalam juta) X XY X 2 Y’ 2006 2007 2008 2009 2010 5,0 5,6 6,1 6,7 7,2 - 2 - 1 0 1 2 - 10,0 - 5,6 0 6,7 14,4 Jumlah 30,6 0 5,5
- 100. 100 a. Untuk dataganjil Tahun Jumlah Pelanngan (dalam juta) X XY X 2 Y’ 2006 2007 2008 2009 2010 5,0 5,6 6,1 6,7 7,2 - 2 - 1 0 1 2 - 10,0 - 5,6 0 6,7 14,4 4 1 0 1 4 Jumlah 30,6 0 5,5 10
- 101. 101 12,6 5 65,30 === ∑ n Y a 55,0 10 5,5 2 === ∑ ∑ X XY b Y’ = 6,12+ 0,55 t Tahun dasar 2008 Unit t 1 tahun ; Y jumlah pelanggan dlm juta
- 102. 102 a. Untuk datagenap Tahun Jumlah Pelanggan (dalam juta) 2005 2006 2007 2008 2009 2010 4,2 5,0 5,6 6,1 6,7 7,2 Jumlah 34,8
- 103. 103 a. Untuk datagenap Tahun Jumlah Pelanggan (dalam juta) X XY X 2 Y’ 2005 2006 2007 2008 2009 2010 4,2 5,0 5,6 6,1 6,7 7,2 Jumlah 34,8
- 104. 104 a. Untuk datagenap Tahun Jumlah Pelanggan (dalam juta) X XY X 2 Y’ 2005 2006 2007 2008 2009 2010 4,2 5,0 5,6 6,1 6,7 7,2 - 5 - 3 - 1 1 3 5 Jumlah 34,8 0
- 105. 105 a. Untuk datagenap Tahun Jumlah Pelanggan (dalam juta) X XY X 2 Y’ 2005 2006 2007 2008 2009 2010 4,2 5,0 5,6 6,1 6,7 7,2 - 5 - 3 - 1 1 3 5 - 21 - 15 5,6 6,1 20,1 36 Jumlah 34,8 0 20,61
- 106. 106 a. Untuk datagenap Tahun Jumlah Pelanggan (dalam juta) X XY X 2 Y’ 2005 2006 2007 2008 2009 2010 4,2 5,0 5,6 6,1 6,7 7,2 - 5 - 3 - 1 1 3 5 - 21 - 15 - 5,6 6,1 20,1 36 25 9 1 1 9 25 Jumlah 34,8 0 20,61 70
- 107. 107 80,5 6 8,34 === ∑ n Y a 2944,0 70 61,20 2 === ∑ ∑ X XY b Y’ = 5,80+ 0,2944 t Tahun dasar jan 2008/ des 2007 Unit ½ tahun ; Y jumlah pelanggan dlm juta
- 108. 108 1. TREND e. MetodeRata-rata Bergerak/Rata-rata Berpindah (Moving Average Method)
- 109. 109 Tahun Jumlah Pelanggan (dalam juta) Jumlah bergerak selama3 thn Rata-rata bergerak per 3 th 2005 2006 2007 2008 2009 2010 4,2 5,0 5,6 6,1 6,7 7,2 14,8 16,7 18,4 20,0 4,94 5,57 6,13 6,67
- 110. 2. Tentukan jumlahpelanggan PT. ”XYZ” pada tahun 2013 110
- 111. 111 Persamaan trend adalah: Y’ = 6,12 + 0,55X Tahun dasar 2008 Unit X : 1 tahun Unit Y : jumlah pelanggan PT. “XYZ” dlm juta
- 112. 112 2. Peramalan Pelanggan PTTelkom pada tahun 2013 Y’ = 6,12 + 0,55 (5) = 8,87 Jumlah pelanggan PT. “XYZ” pada bulan juni 2013 berkisar 8,87 juta orang
- 113. 3. Rubahlah persamaantrendnya menjadi bulanan dgn thn dsr 2010 113
- 114. 114 3. Perubahan Tahundasar, var Y dan var X Tahun 2010 , Y’ = 6,12 + 0,55 (2) = 7,22 a. Y’ = 7,22 + 0,55 X Tahun dasar 2010 Unit X : 1 tahun Unit Y : banyaknya pelanggan PT. “XYZ” per tahun
- 115. 115 3. Perubahan Tahundasar, var Y dan var X b. Y’ = 0,6017 + 0,046 X Tahun dasar 2010 Unit X : 1 tahun Unit Y : banyaknya pelanggan PT. “XYZ” per bulan
- 116. 116 3. Perubahan Tahundasar, var Y dan var X c. Y’ = 0,6017 + 0,00038 X Tahun dasar 2010 Unit X : 1 bulan Unit Y : banyaknya pelanggan PT. “XYZ” per bulan
- 117. 4. Rubahlah persamaantrend (1) menjadi - trend semesteran dengan waktu dasar semester I - trend triwulan dengan waktu dasar triwulan II - trend bulanan dengan waktu dasar 15 Juli 2009 117
- 118. 118 Persamaan trend adalah: Y’ = 6,12 + 0,55X Tahun dasar 2008 Unit X : 1 tahun Unit Y : jumlah pelanggan PT. “XYZ” dlm juta
- 119. 119 4. Merubah persamaantrend dari hasil perhitungan menjadi : a. Trend semesteran dengan waktu dasar semester I (april 2008) Y’ = 6,12 + 0,55 X Y’ = ½ { 6,12 + ( 0,55 X )/ 2 }
- 120. 120 4. Merubah persamaantrend dari hasil perhitungan menjadi : a. Trend semesteran dengan waktu dasar semester I (april 2008) Y’ = 6,12 + 0,55 X Y’ = ½ { 6,12 + ( 0,55 X )/ 2 } = 3,06 + 0,1375 ( – 0,5 ) + 0,1375 X = 2,99125 + 0,1375 X
- 121. 121 4. Merubah persamaantrend dari hasil perhitungan menjadi : b. Trend triwulanan dengan waktu dasar triwulan II ( 15 Mei 2008) Y’ = 6,12 + 0,55X Y’ = ¼ { 6,12 + ( 0,55 X ) /4 } = 1,53 + 0,0344 ( – 0,5 ) + 0,0344 X = 1,5128 + 0,0344 X
- 122. 122 4. Merubah persamaantrend dari hasil perhitungan menjadi : c. Trend bulanan dengan waktu dasar 15 Juli 2008. Y’ = 6,12 + 0,55X Y’ = 1/12 { 6,12 + ( 0,55 X ) /12 } = 0,51 + 0,0038 ( 0,5 ) + 0,0038 X = 0,5119 + 0,0038 X
- 123. 123 5. Tentukan banyaknyapelanggan PT. “XYZ” pada tahun 20013 dari jawaban (4) a. Y’ = 2,99125 + 0,1375 ( 10,5 ) = 4,435 b. Y’ = 1,5128 + 0,0344 ( 20,5 ) = 2,218 c. Y’ = 0,5119 + 0,0038 ( 60 ) = 0,7399
- 124. 124 5. Tentukan banyaknyapelanggan PT. “XYZ” pada tahun 20013 dari jawaban (4) a. Y’ → 4,435 x 2 = 8,87 b. Y’ → 2,218 x 4 = 8,87 c. Y’ → 0,7399 x 12 = 8,88 (krn pembulatan)
- 125. 125 2008 2009 20102011 2012 20013 J F M A M J J A S O N D J F M A M J J A S O N D J F M A M J J A S O N D J F M A M J J A S O N D J F M A M J J A S O N D J F M A M J J A S O N D
- 126.
- 127. 127 Tabel dibawah iniadalah tentang data panen jagung dari tahun 2003 – 2009 Tahun Panen Jagung 2003 2004 2005 2006 2007 2008 2009 40 44 46 48 52 58 60
- 128. 128 Pertanyaannya : a. Gambarkangaris trend b. Tentukan persamaan garisnya dengan metoda kuadrat terkecil. c. Tentukan besarnya jumlah panen jagung pada tahun 2012. d. Rubahlah persamaan trendnya menjadi bulanan dengan tahun dasar 2009
- 129. 129 e. Rubahlah persamaantrend (b) menjadi - trend semesteran dengan waktu dasar semester I - trend triwulan dengan waktu dasar triwulan II - trend bulanan dengan waktu dasar 15 Juli 2009 f. Lakukan peramalan utk tahun 2012 dari jawaban e