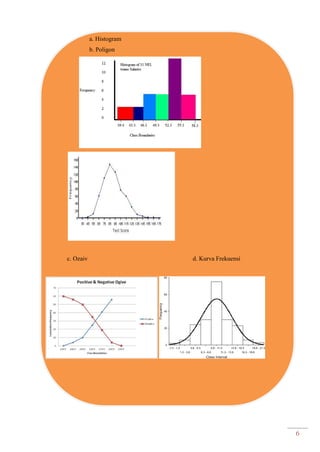
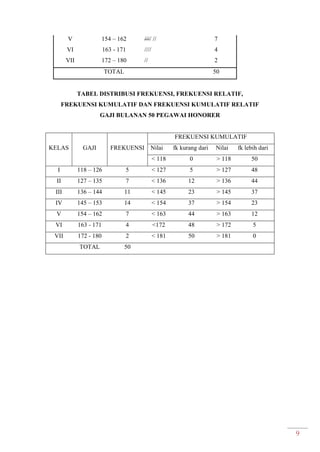
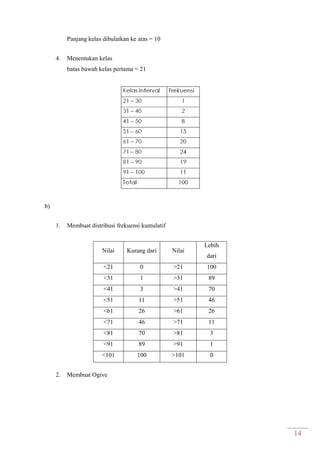
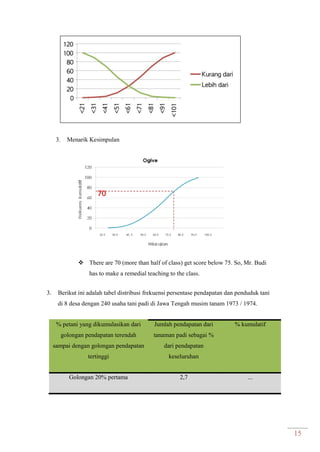
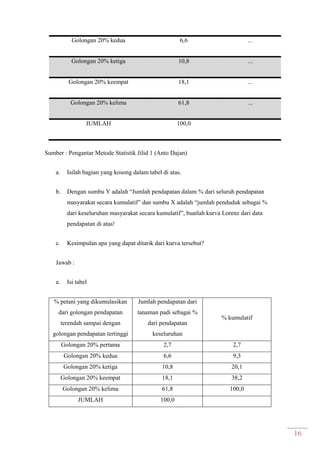
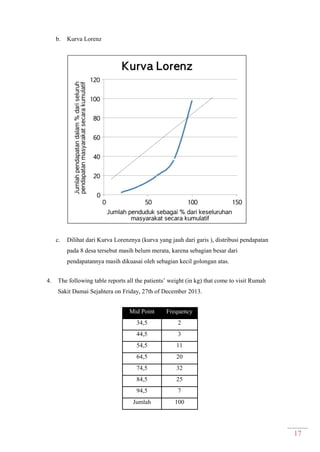
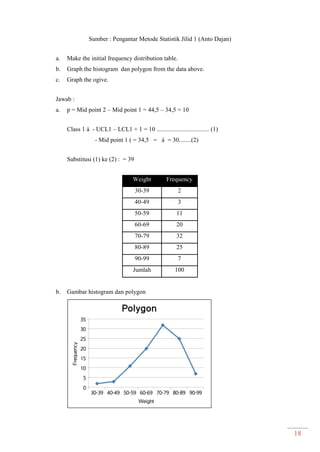
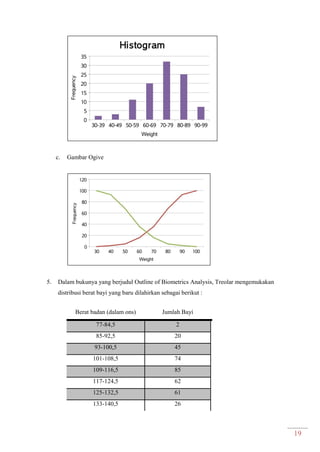
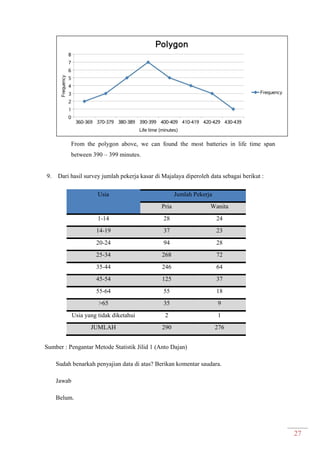
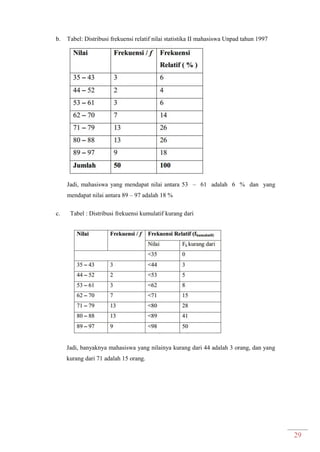
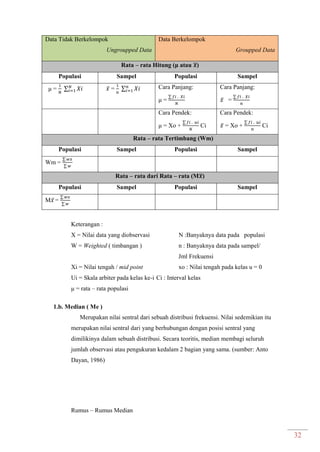
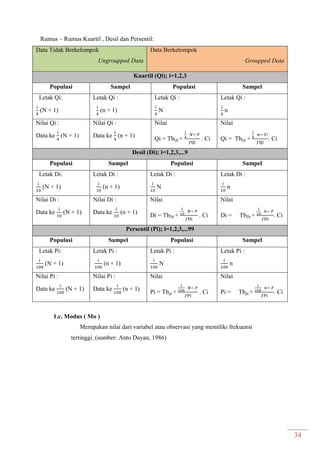
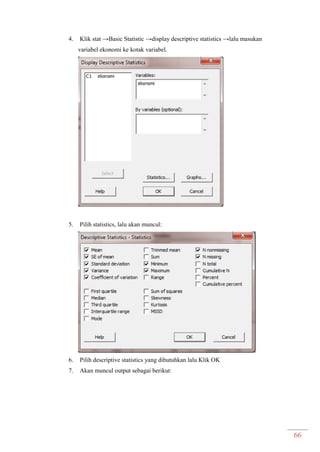
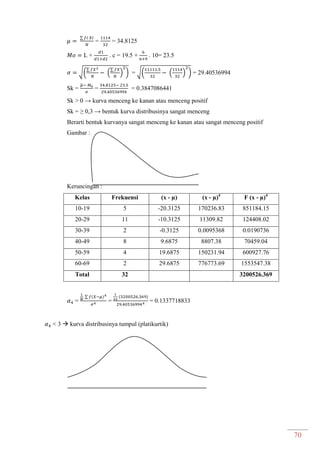
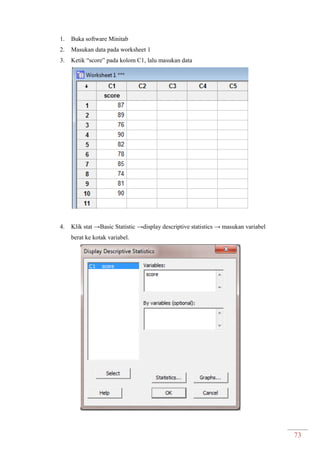
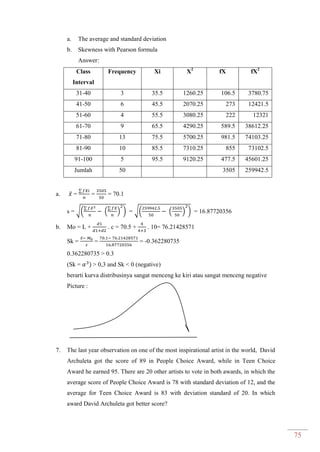
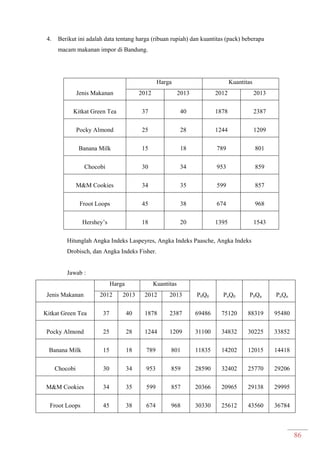
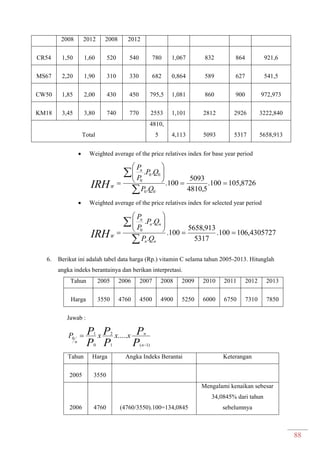
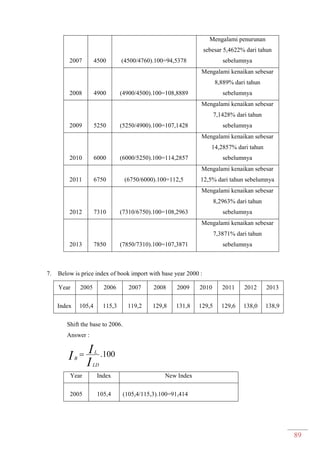
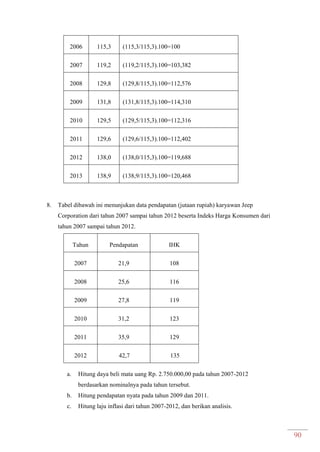
Dokumen ini adalah modul praktikum statistika I yang mencakup berbagai topik seperti distribusi frekuensi, ukuran gejala pusat, dan analisis deret berkala. Modul ini disusun oleh tim asisten dosen di Fakultas Ekonomi dan Bisnis Universitas Padjadjaran dan berisi panduan serta metode dalam menyusun dan menganalisis distribusi data. Terdapat juga contoh soal dan tabel distribusi frekuensi untuk berbagai contoh data.