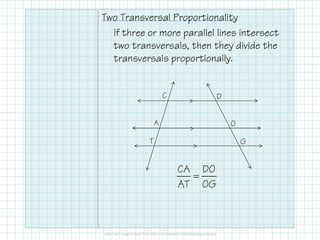
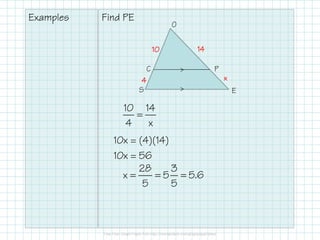
The document explains properties of similar triangles, including the triangle proportionality theorem, which states that a line parallel to a side of a triangle divides the other two sides proportionally. It also covers methods of indirect measurement using proportionality and similar figures to calculate lengths, along with examples for clarity. The document emphasizes the application of these concepts through problems involving scale drawings and real-life situations.

1. Similar Triangle Properties
The student is able to (I can):
• Use properties of similar triangles to find segment
lengths.lengths.
• Apply proportionality and triangle angle bisector
theorems.
• Use ratios to make indirect measurements
• Use scale drawings to solve problems.

2. Triangle Proportionality Theorem
If a line parallel to a side of a triangle
intersects the other two sides then it
divides those sides proportionally.
P
A
C>
AP AC
PS CE
=
S E>
PC SE
Note: This ratio is not the same as the
ratio between the third sides!
≠
AP PC
PS SE

3. Triangle Proportionality Theorem Converse
If a line divides two sides of a triangle
proportionally, then it is parallel to the
third side.
P
A
C> PC SE
S E>
AP AC
PS CE
=

4. Two Transversal Proportionality
If three or more parallel lines intersect
two transversals, then they divide the
transversals proportionally.
O
D
A
C
>
G
O
T
A
>
>
CA DO
AT OG
=

5. Examples Find PE
S
C
O
P
E
10101010 14141414
4444
10 14
4 x
=
xxxx
>
>
10x = (4)(14)
10x = 56
4 x
=
28 3
x 5 5.6
5 5
= = =

6. Example Verify that
H
O
R
SE
HE OS
15
10
12 8
(15)(8) = (10)(12)?
120 = 120 Therefore,
=
15 10
?
12 8
HE OS

7. Example Solve for x.
>
>
>
x
96
10
6x = (10)(9)
6x = 90
x = 15
10 x
6 9
=

8. indirect
measurement
Any method that uses formulas, similar
figures, and/or proportions to measure an
object.
Example: An 8 foot tall stick casts a
6 foot shadow. At the same time, a tall
flagpole casts an 18 foot shadow. How tall
is the flagpole?
6
8
18
x
The triangles are similar by AA~.
8 x
6 18
= 6x = 144 → x = 24 feet

9. Example Miriam saw a mirror on the ground and
noticed that she could see the top of
Reunion Tower in the mirror. Her line of
sight was 5’ above the ground, and the
mirror was 2’ away from her. She measured
the distance from that position to the
base of Reunion Tower, and it was 224 feet.
How high is Reunion Tower?
The reflection creates congruent angles, so
the triangles are similar by AA~.

10. Example
5’
2’ 224’
x
5 x
2 224
=
2 224
2x 1120
x 560 ft.
=
=
=

11. Example
According to the map’s scale, 1 in = 100 mi.
If it measures 2.75 in. from Ft. Worth toIf it measures 2.75 in. from Ft. Worth to
San Antonio, how far away are the two
cities?
1 2.75
100 x
x 275 mi.
=
=