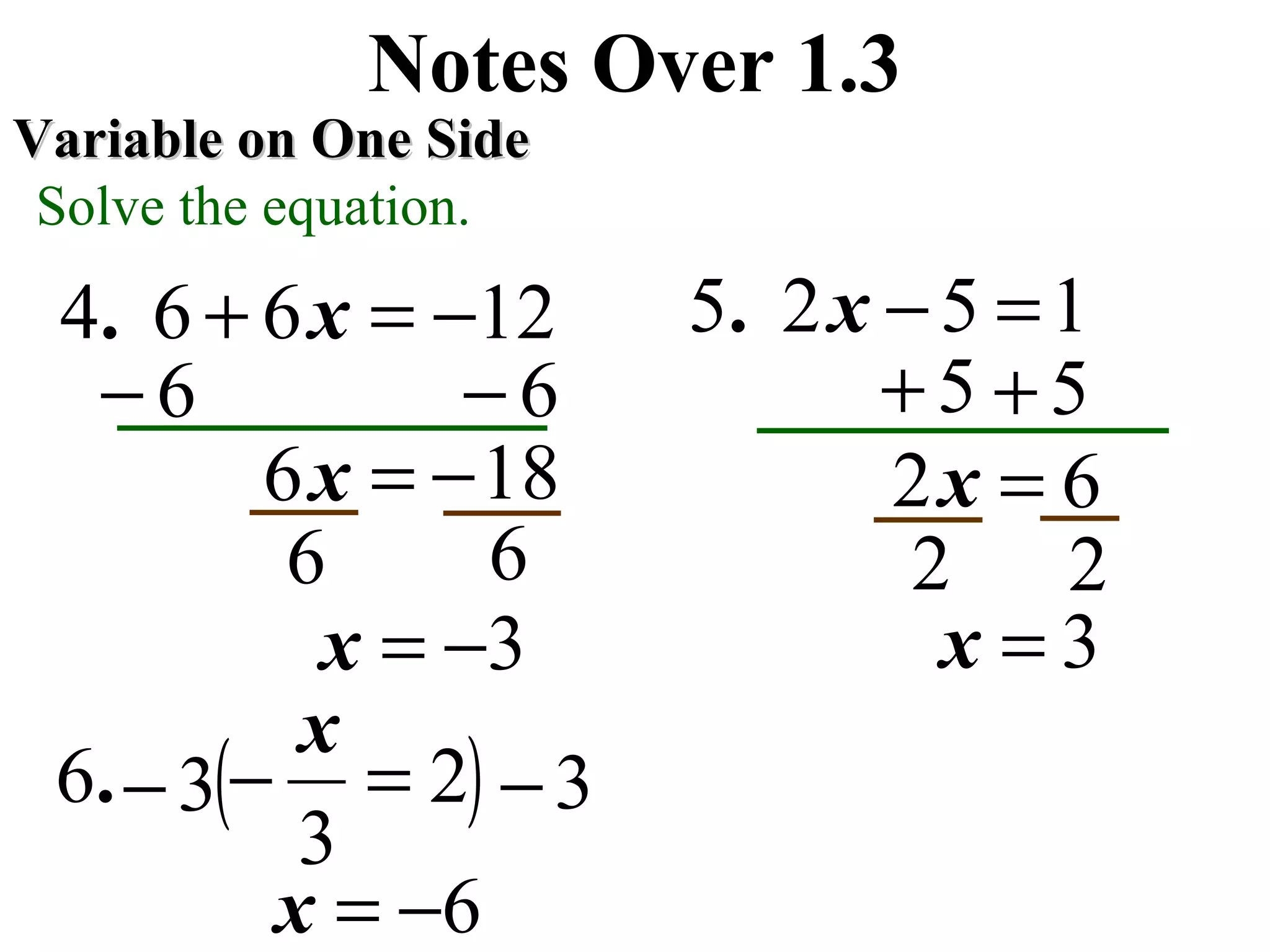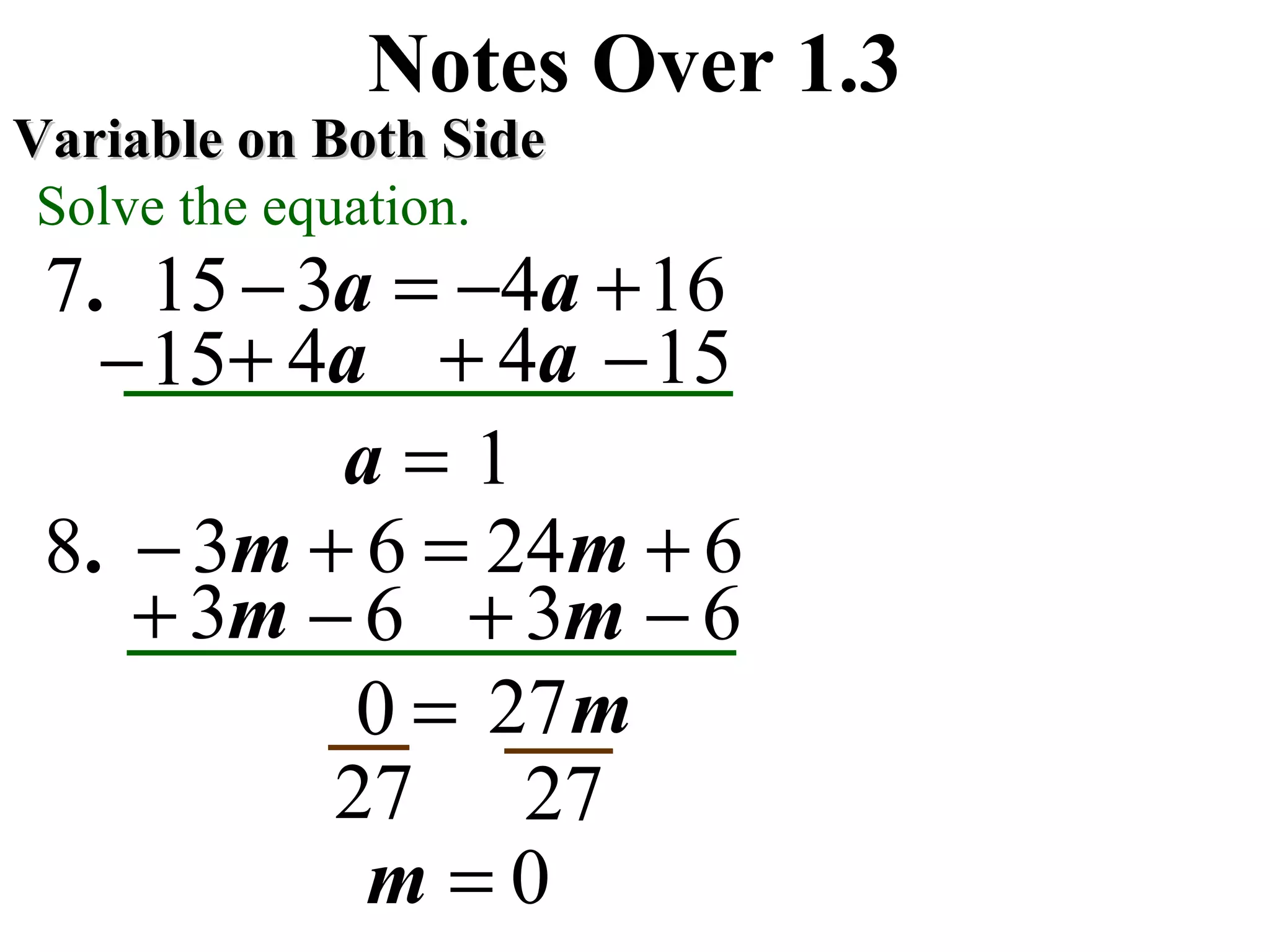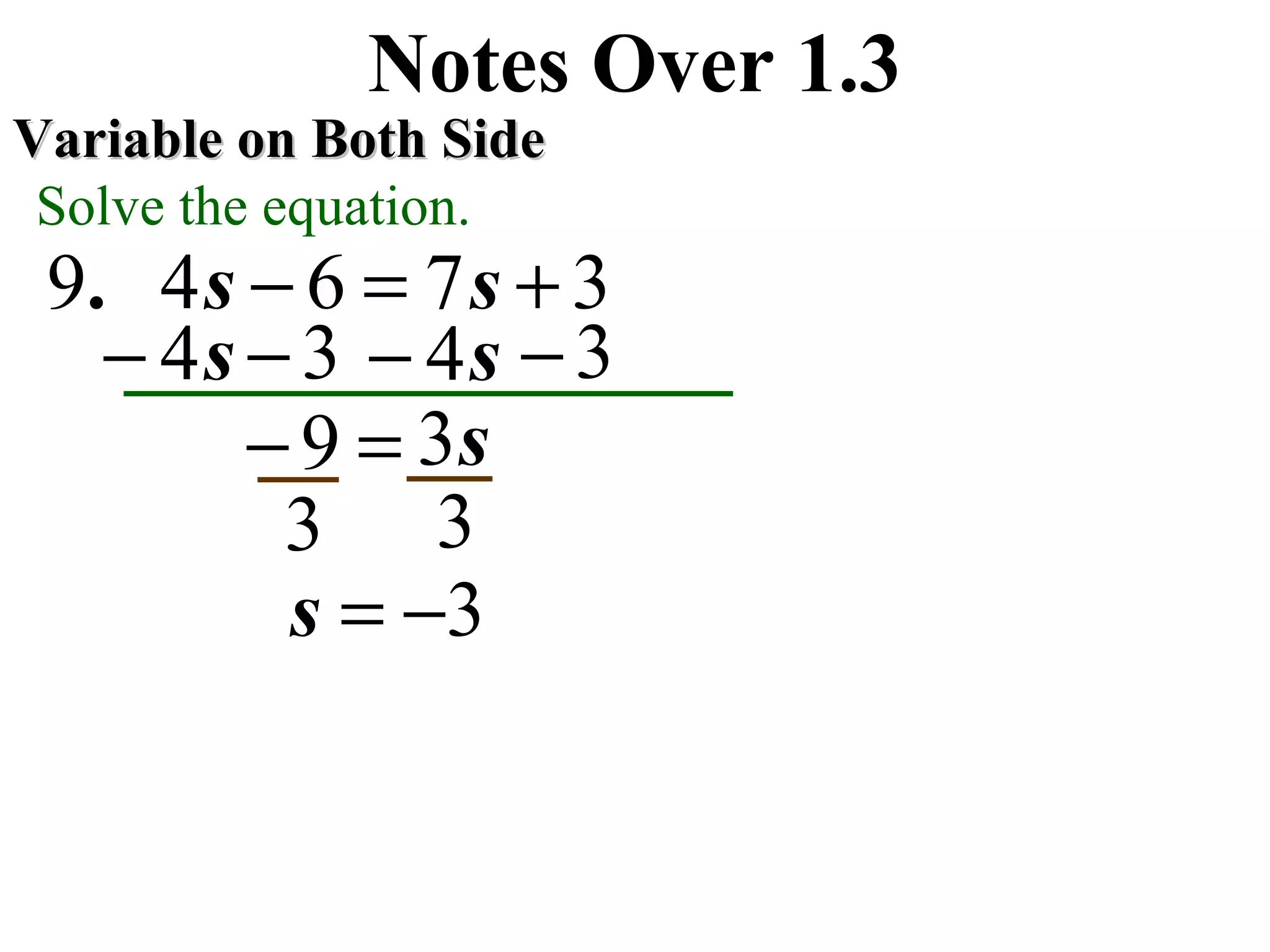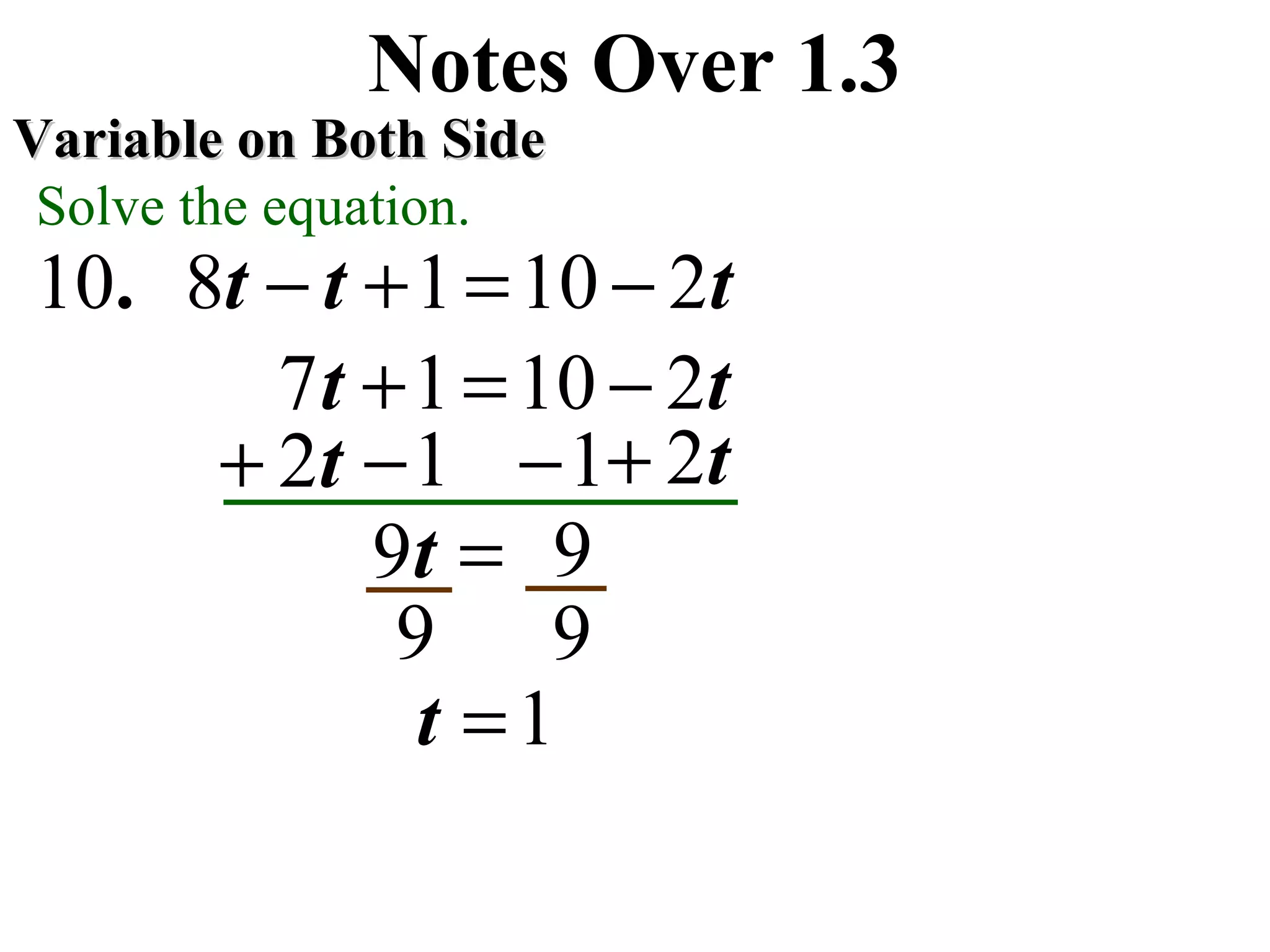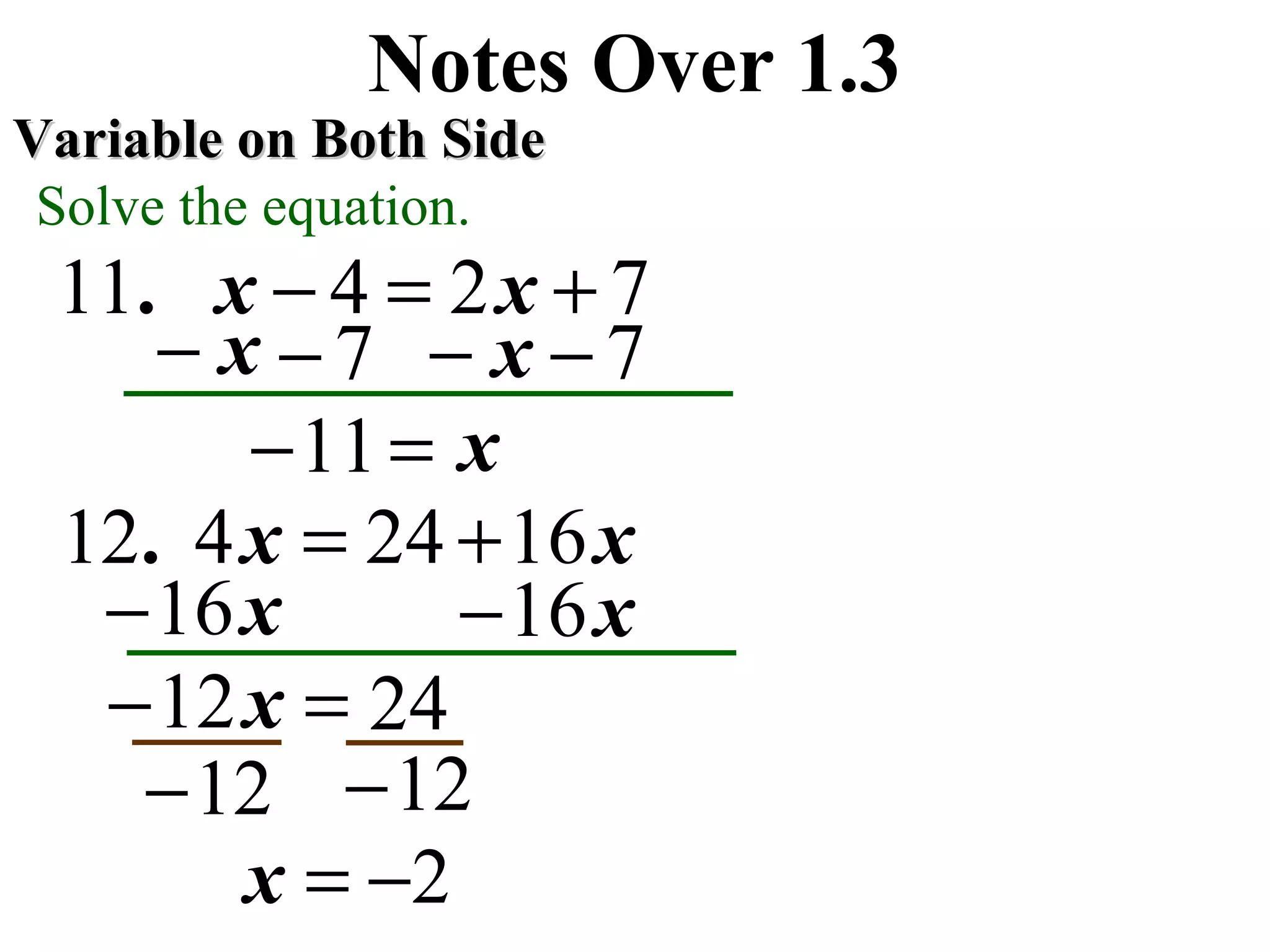This document contains step-by-step solutions to various equations involving variables on one or both sides. The equations include integers, fractions, and variables with exponents. The solutions demonstrate techniques such as isolating the variable, using the distributive property, and rationalizing denominators.

1. Notes Over 1.3
It’s time to stop
“daydreaming”
and start applying
“mental math”

2. 231 −−= x.
Notes Over 1.3
Variable on One SideVariable on One Side
Solve the equation.
2+2+
x−
6182 +=− y.
6− 6−
24−
593 =− z.
=5
5−=x y=
9− 9−
z− 4−=
4=z

3. 12664 −=+ x.
Notes Over 1.3
Variable on One SideVariable on One Side
Solve the equation.
6−6−
18−
1525 =−x.
5+5+
x2=x6
3−=x
6=
6 6 2 2
3=x
2
3
6 =−
x
. (3− ) 3−
6−=x

4. 1643157 +−=− aa.
Notes Over 1.3
Variable on Both SideVariable on Both Side
Solve the equation.
a4+a4+
1=a
15− 15−
624638 +=+− mm.
m3+ m3+
m27=0
6−6−
2727
0=m

5. 37649 +=− ss.
Notes Over 1.3
Variable on Both SideVariable on Both Side
Solve the equation.
s4− s4−
s3=−9
3−3−
33
3−=s

6. ttt 2101810 −=+−.
Notes Over 1.3
Variable on Both SideVariable on Both Side
Solve the equation.
t2+t2+
9=t9
1− 1−
9 9
1=t
tt 21017 −=+

7. 72411 +=− xx.
Notes Over 1.3
Variable on Both SideVariable on Both Side
Solve the equation.
x− x−
x=−11
7−7−
xx 1624412 +=.
x16−x16−
24=− x12
12− 12−
2−=x

8. ( ) ( )221235.13 −−=+− xx
Notes Over 1.3
Using the Distributive PropertyUsing the Distributive Property
Solve the equation.
x5
x2+x2+
7=x7
3+ 3+
7 7
1=x
1215+− x2−= 4+
4235 +−=− xx

9. ( ) ( ) 7132414 =++−− kk.
Notes Over 1.3
Using the Distributive PropertyUsing the Distributive Property
Solve the equation.
k4−
4−=− k
11− 11−
4=k
8+ k3+ 73 =+
k− 711=+

10. ( )12215 +=− xx.
Notes Over 1.3
Using the Distributive PropertyUsing the Distributive Property
Solve the equation.
x2−
2=− x4
x2−x2−
x2= 2+
4− 4−
2
1
−=x

11. ( )529316 −=− xx.
Notes Over 1.3
Using the Distributive PropertyUsing the Distributive Property
Solve the equation.
93 −x
1−=x
x2−x2−
x2= 10−
9+ 9+

12. ( )25
3
2
617 −= nn.
Notes Over 1.3
Solving an Equation with FractionsSolving an Equation with Fractions
Solve the equation.
n10−n10−
4−=n8
8 8
2
1
−=n
=n18 n10 4−

13. 41
4
3
18 =+x.
Notes Over 1.3
Solving an Equation with FractionsSolving an Equation with Fractions
Solve the equation.
4− 4−
12=x3
3 3
4=x
x3 =+ 4 16
(4 )4(4

14. xx 4
3
2
2
1
19 =−.
Notes Over 1.3
Solving an Equation with FractionsSolving an Equation with Fractions
Solve the equation.
x3− x3−
x21=− 4
2121
21
4
−=x
3
=− 4 x24
(6 )6(6
x3
2

15. 1
3
2
5
3
20 += xx.
Notes Over 1.3
Solving an Equation with FractionsSolving an Equation with Fractions
Solve the equation.
x10−x10−
15=− x
15−=x
3
x10= 15+
(15 )15(15
x9
5

16. Notes Over 1.3