KEY

1. บทที่ 1
ลําดับอนันตและอนุกรมอนันต
(20 ชั่วโมง)
ลําดับอนันตและอนุกรมอนันตที่จะกลาวถึงในบทนี้ เปนเรื่องเกี่ยวกับลิมิตของลําดับ
ทฤษฎีบทตาง ๆ เกี่ยวกับลิมตของลําดับ การหาผลบวกของอนุกรมอนันต และการใชสญลักษณ
ิ ั
แทนการบวก ตลอดจนโจทยที่แสดงใหเห็นการนําความรูที่กลาวมาไปใชในการแกปญหาตาง ๆ

ผลการเรียนรูที่คาดหวัง
1. หาลิมิตของลําดับอนันตโดยอาศัยทฤษฎีบทเกี่ยวกับลิมิตได
2. หาผลบวกของอนุกรมอนันตได
3. นําความรูเรื่องลําดับและอนุกรมไปใชแกปญหาได
ผลการเรียนรูที่คาดหวังดังกลาวเปนผลการเรียนรูที่สอดคลองกับมาตรฐานการเรียนรู
ชวงชั้นที่ 4 ทางดานความรู ในการจัดการเรียนรูผูสอนตองคํานึงถึงมาตรฐานการเรียนรูดาน
ทักษะ/ กระบวนการทางคณิตศาสตรดวยการสอดแทรกกิจกรรมหรือโจทยปญหาที่จะสงเสริมให
ผูเรียนเกิดทักษะ / กระบวนการทางคณิตศาสตรที่จําเปนอันไดแกความสามารถในการแกปญหา
การใหเหตุผล การสื่อสาร การสื่อความหมายทางคณิตศาสตรและการนําเสนอ การเชื่อมโยง
ความรูตาง ๆ ทางคณิตศาสตรและเชื่อมโยงคณิตศาสตรกับศาสตรอื่น และการคิดริเริ่มสรางสรรค
นอกจากนั้น กิจกรรมการเรียนรูควรสงเสริมใหผูเรียนตระหนักในคุณคาและมีเจตคติที่ดีตอวิชา
คณิตศาสตร ตลอดจนฝกใหผูเรียนทํางานอยางเปนระบบ มีระเบียบวินัย รอบคอบ มีความ
รับผิดชอบ มีวิจารณญาณและมีความเชื่อมันในตนเอง
่
สาระการเรียนรูคณิตศาสตรเพิ่มเติมเปนสาระการเรียนรูสาหรับการศึกษาตอและอาชีพ
ํ
ดังนั้นในการจัดการเรียนรูในสาระนี้ ผูสอนควรสงเสริมใหผูเรียนไดฝกทักษะการคิดวิเคราะห

โดยคํานึงถึงความสมเหตุสมผลของขอมูล ดังนั้น ในการสอนแตละสาระผูสอนจําเปนตองศึกษา
สาระนั้น ๆ ใหเขาใจถองแทเสียกอนแลวเลือกวิธีสอนใหเหมาะสม เพื่อทําใหการจัดการเรียนรู
ไดผลดี

2. 2
ขอเสนอแนะ
1. รูปแบบการกําหนดลําดับทําไดหลายแบบ ผูสอนควรย้าและยกตัวอยางใหผูเรียนเห็นวา
ํ
การกําหนดลําดับโดยการแจงพจนแลวหาพจนทวไปของลําดับนั้น อาจหาพจนทั่วไปไดตางกัน
ั่
(ดูหนังสือเรียนหนา 3 – 4 และคูมือครูสาระการเรียนรูพื้นฐาน ชันมัธยมศึกษาปที่ 5 เรื่องลําดับ
 ้
และอนุกรม หนา 2)
2. ผูสอนควรทบทวนเรื่องลําดับจํากัด ลําดับเลขคณิตและลําดับเรขาคณิต และอนุกรม
จํากัดกอนที่จะขยายความตอและกลาวถึงลําดับอนันตและอนุกรมอนันต ผูสอนควรบอกผูเรียน
ดวยวา ยังมีลําดับอื่น ๆ อีกมากมายที่ไมใชลําดับเลขคณิตหรือลําดับเรขาคณิต ผูสอนอาจใช
ประโยชนจากเว็บไซต The On-Line Encyclopedia of Integer Sequences ซึ่งเก็บรวบรวมลําดับ
ตาง ๆ ไวใหคนหาไดมากมาย ที่ http://www.research.att.com/~njas/sequences/ หรือผูสอนอาจ
ใหผูเรียนชวยกันสรางลําดับใหมเอง
3. ในเรื่องความสัมพันธเวียนเกิด ผูสอนอาจเพิ่มเติมแบบฝกหัดสําหรับผูเรียนที่สนใจ
คณิตศาสตรเปนพิเศษ ผูสอนอาจใหผูเรียนกําหนดลําดับที่กําหนดใหตอไปนี้โดยใชความสัมพันธ
เวียนเกิด
(1) 1, 2, 4, 8, 16, ..., 2n–1 , ...
เพราะวา a1 = 1
a2 = 2 = 2(1) = 2a1
a3 = 4 = 2(2) = 2a2
a4 = 8 = 2(4) = 2a3
an = 2n–1 = 2an–1
ดังนั้น กําหนดลําดับนี้โดยใชความสัมพันธเวียนเกิดไดเปนลําดับ an = 2an–1
เมื่อ n ≥ 2, a1 = 1
(2) 1, –1, 1, –1, ..., (–1)n+1, ...
เพราะวา a1 = 1
a2 = –1 = (–1)(1) = (–1)a1
a3 = 1 = (–1)(–1) = (–1)a2
a4 = –1 = (–1)(1) = (–1)a3
an = (–1)an–1
ดังนั้น กําหนดลําดับนี้โดยใชความสัมพันธเวียนเกิดไดเปนลําดับ an = (–1)an–1
เมื่อ n ≥ 2, a1 = 1

3. 3
(3) กําหนดลําดับ 5, 9, 13, 17, ..., 4n + 1, ... โดยใชความสัมพันธเวียนเกิดไดเปน
ลําดับ an = an–1 + 4 เมื่อ n ≥ 2 , a1 = 5
(4) กําหนดลําดับ 1, 3, 9, 27, ..., 3n–1, ... โดยใชความสัมพันธเวียนเกิดไดเปนลําดับ
an = 3an–1 เมื่อ n ≥ 2 , a1 = 1
(5) กําหนดลําดับ 1, 1, 1, 1, ..., 1, ... โดยใชความสัมพันธเวียนเกิดไดเปนลําดับ
an = an–1 เมื่อ n ≥ 2, a1 = 1
n(n + 1)
(6) กําหนดลําดับ 1, 3, 6, 10, 15, ..., , ... โดยใชความสัมพันธเวียนเกิด
2
ไดเปนลําดับ an = an–1+ n เมื่อ n ≥ 2, a1 = 1
(7) กําหนดลําดับ 5, 10, 30, 120, ..., 5n!, ... โดยใชความสัมพันธเวียนเกิดไดเปน
ลําดับ an = nan–1 เมื่อ n ≥ 2, a1 = 5
4. การทบทวนสูตรพจนที่ n ของลําดับเลขคณิต (หนา 7) และสูตรพจนที่ n ของลําดับ
เรขาคณิต (หนา 9) โดยการเขียนยอนกลับ ผูสอนอาจจะแสดงตัวอยางที่เปนตัวเลขใหผูเรียนพิจารณา
ประกอบไปดวยสัก 2 – 3 ตัวอยางกอนที่จะสรุปเปนกรณีทั่วไป และถาผูสอนพิจารณาแลววา
แนวทางของเรื่องเดียวกันทีนําเสนอไวในหนังสือเรียนสาระการเรียนรูพื้นฐาน ชันมัธยมศึกษา
่  ้
ปที่ 5 เขาใจงายกวา ก็อาจขามสวนนี้ไปก็ได อยางไรก็ตาม ผูสอนควรชี้ใหผูเรียนเห็นแนวทาง
ที่แตกตางของทั้งสองวิธี
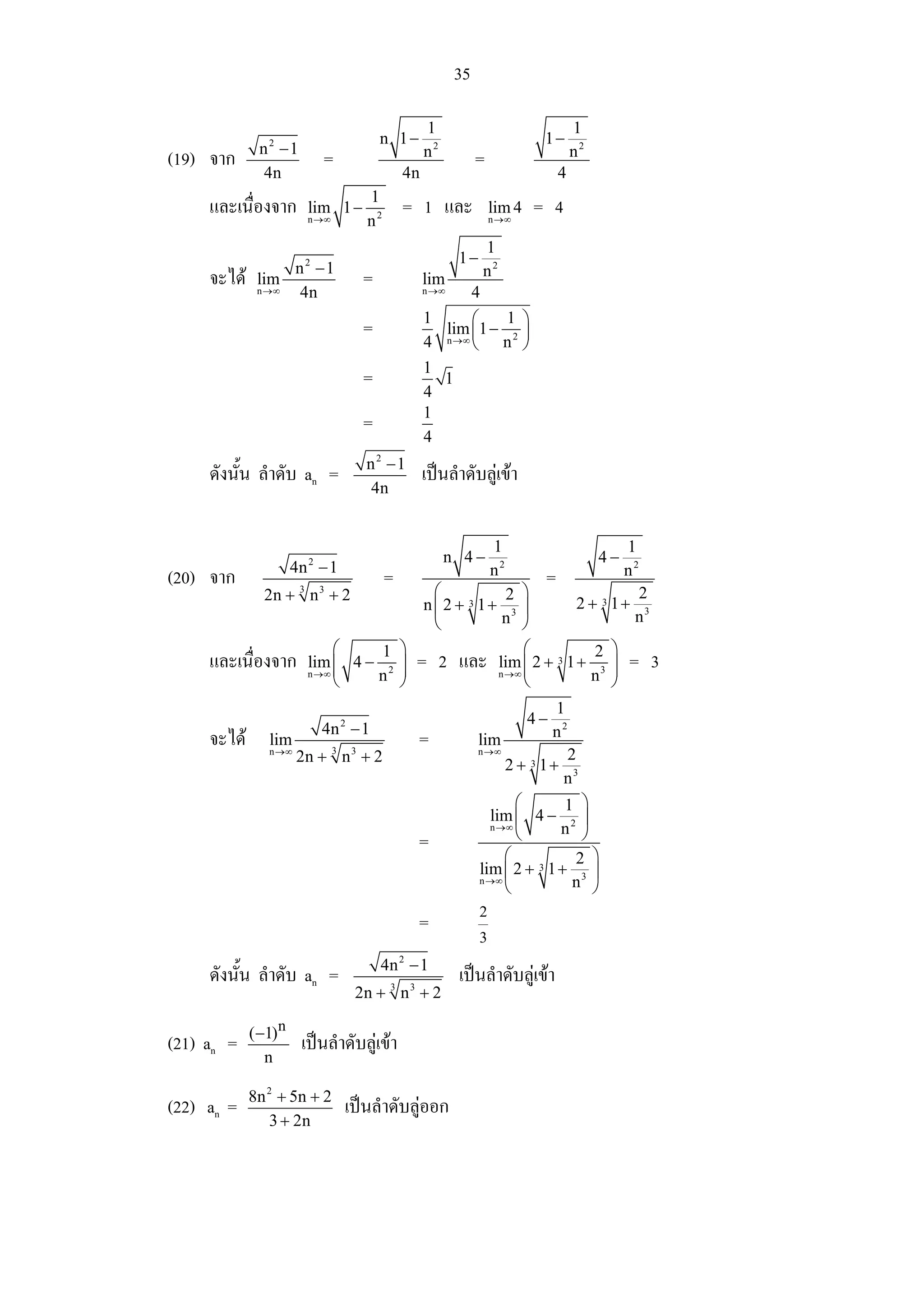
5. จากการพิจารณาลิมิตของลําดับ ทําใหแบงลําดับออกเปน 2 ประเภท คือ ลําดับ
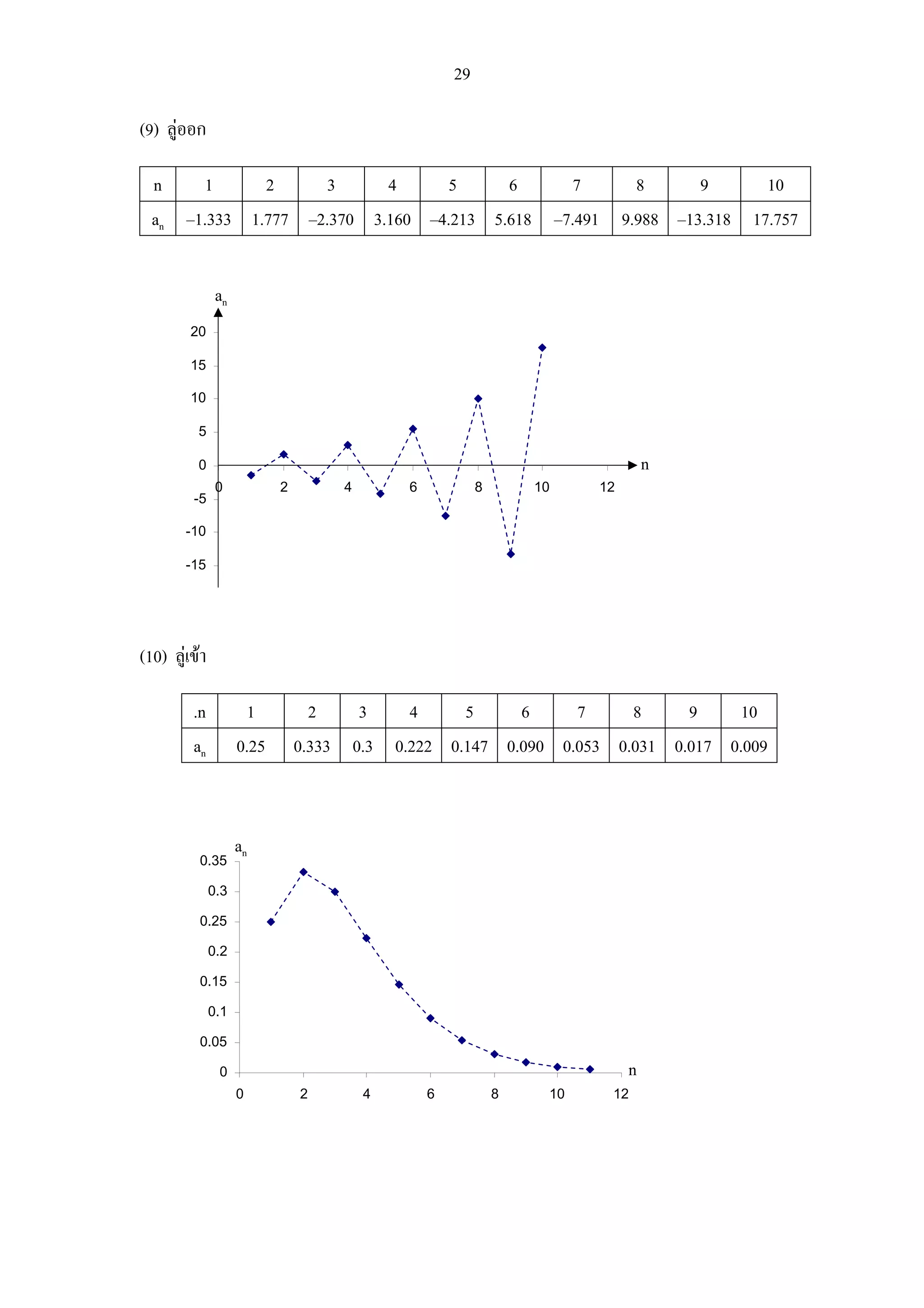
ที่มีลิมิต เรียกวา ลําดับลูเขา และลําดับที่ไมมีลิมิต เรียกวา ลําดับลูออก สําหรับลําดับลูออก
ถาพิจารณาลําดับจากกราฟจะแบงออกเปน 3 ประเภทคือ
(1) ลําดับลูออกซึ่งพจนที่ n มีคามากขึ้นเรื่อย ๆ เมือ n มีคามากขึ้นโดยไมมีที่สนสุด
่  ิ้
เชน 1, 2, 4, ..., 2 n–1 , ...
(2) ลําดับลูออกซึ่งพจนที่ n มีคาลดลงเรื่อย ๆ เมื่อ n มีคามากขึ้นโดยไมมีที่สิ้นสุด
เชน –1, –3, –5, ..., –(2n – 1), ...
(3) ลําดับลูออกซึ่งมีลักษณะแตกตางจากลําดับในขอ (1) และขอ (2) ซึงเรียกวา
่
ลําดับแกวงกวัด เชน an = (–1)n , bn = (–1)n n
6. การเชื่อมโยงมโนทัศนเรื่องลิมิตของลําดับกับรูปภาพ ผูสอนอาจเริ่มจากการคํานวณ

แลวเขียนกราฟ และพิจารณาแนวโนมวา เมื่อ n มีคามากขึ้นเรื่อย ๆ กราฟของลําดับ an จะเปน
อยางไร ผูสอนอาจแนะนําการเขียนกราฟโดยใชเครื่องมือตาง ๆ เชน กระดาษกราฟ เครื่องคํานวณ
โปรแกรม Geometer’s Sketchpad หรือโปรแกรมประเภทตารางทํางาน เชน Microsoft Excel
7. หนังสือเรียนไมไดแสดงวิธีการพิสูจนทฤษฎีบทตาง ๆ เกี่ยวกับลิมิตไว ผูสอนควรให
ผูเรียนพิจารณาคา an โดยตรง หรือทดลองเขียนกราฟของลําดับ an แลวพิจารณาแนวโนมของกราฟ

4. 4
1 1
เชน ใหผูเรียนพิจารณาลําดับ an = และ an = 1
เพื่อนําไปสูการยอมรับทฤษฎีบทที่วา
n3
n 3
1
lim
n →∞ n r
= 0 เมื่อ r เปนจํานวนจริงบวกใด ๆ ผูเรียนควรอธิบายไดวา เมื่อ n มีคามากขึ้นอยาง
1
1 1
ไมมีที่สิ้นสุด n3 และ n3 จะมีคามากขึ้นอยางไมมีที่สิ้นสุดดวย ซึ่งจะทําให และ 1
มีคา
n3
n 3
นอยลงและเขาใกล 0
1
ใหผูเรียนพิจารณาลําดับ an = n4 และ an = n เพื่อนําไปสูการยอมรับทฤษฎีบท
4
ที่วา nlim n r หาคาไมได เมื่อ r เปนจํานวนจริงบวกใด ๆ ผูเรียนควรอธิบายไดวา เมื่อ n มี
→∞

1
คามากขึ้นอยางไมมีที่สิ้นสุด n4 และ n4 จะมีคามากขึ้นอยางไมมีที่สิ้นสุดดวย
n n
⎛1⎞ ⎛ 1⎞
ใหผูเรียนพิจารณาลําดับ an = ⎜ ⎟ และ an = ⎜− ⎟ เพื่อนําไปสูการยอมรับ
⎝ 3⎠ ⎝ 4⎠
ทฤษฎีบทที่วา lim r n
n →∞
= 0 เมื่อ r เปนจํานวนจริง และ r <1
ใหผูเรียนพิจารณาลําดับ an = 3n และ an = (–4)n เพื่อนําไปสูการยอมรับทฤษฎี
บทที่วา nlim r หาคาไมได เมื่อ r เปนจํานวนจริง และ r > 1
→∞
n
8. ขอความวา “ nlim a n หาคาไมได” มีความหมายเชนเดียวกับขอความ “ลําดับ an
→∞
ไมมลิมต” หรือ “พจนที่ n ของลําดับ an ไมเขาใกลหรือเทากับจํานวนจริง L ใด ๆ เลย” ในบทนี้
ี ิ
ไมมการใชขอความวา “ nlim a n = ∞ ” หรือ “ nlim a n = – ∞ ”
ี →∞ →∞
9. ในหนังสือเรียนหนา 22 ผูสอนควรย้ํากับผูเรียนวา จะใชทฤษฎีบทเกี่ยวกับลิมิตได
a lim a n
เมื่อเงื่อนไขเบืองตนเปนจริงกอนเทานัน เชน จะสรุปวา
้ ้ lim n = n →∞ ไดเมื่อ lim a
n →∞ b n lim b n →∞ n
n →∞ n
และ lim b
n →∞ n
หาคาได และ lim b ≠ 0
n →∞ n
ในกรณีที่ไมสามารถใชทฤษฎีบทเกี่ยวกับลิมิตของลําดับ an โดยตรงได อาจตองจัดรูปของ an
กอนการใชทฤษฎีบทเกียวกับลิมิต ดังปรากฏในหลาย ๆ ตัวอยางในหนังสือเรียน อยางไรก็ตาม
่
ลําดับบางลําดับก็ยังคงใชทฤษฎีบทเกียวกับลิมิตไมไดถึงแมจะพยายามจัดรูปใหแตกตางจากเดิม
่
แลว เชน
2
2n − 3n
พิจารณาลําดับ an =
4n − 5
เนื่องจาก 2
lim (2n − 3n)
n →∞
และ lim (4n − 5)
n →∞
หาคาไมไดทั้งคู ฉะนั้น หากตองการ
2 2
2n − 3n lim (2n − 3n)
หา nlim a n = nlim
→∞ →∞
จึงใชทฤษฎีบทเกี่ยวกับลิมิตที่วา lim a =
n →∞ n
n →∞ ไมได
4n − 5 lim (4n − 5)
n →∞
การจัดรูป an กอนการพิจารณาลิมิตอาจทําไดหลาย ๆ แบบ บางคนอาจทําดังนี้

5. 5
2⎛
3⎞ 3
2
2n − 3n
⎜2 − ⎟
n 2−
= ⎝ n⎠ = n
4n − 5 2⎛4 5 ⎞ 4
−
5
n ⎜ − ⎟
⎝ n n2 ⎠ n n2
กรณีนก็ยงคงใชทฤษฎีบทเกียวกับลิมิตไมได เพราะเปนกรณียกเวน เนื่องจาก
้ี ั ่
⎛4 5 ⎞
−
n →∞ ⎜ n n 2
lim ⎟ =0
⎝ ⎠
2
2n − 3n n ( 2n − 3) 2n − 3
บางคนอาจทําดังนี้ = =
4n − 5 ⎛ 5⎞
4−
5
n⎜4 − ⎟
⎝ n⎠ n
การจัดรูป an เชนนี้กยังคงใชทฤษฎีบทเกี่ยวกับลิมิตไมไดเชนเดียวกัน เพราะ
็
lim (2n − 3) หาคาไมได
n →∞
จะเห็นไดวาการจัดรูป an ทั้งสองแบบไมสามารถชวยสรุปไดวา a n เปนลําดับลูเขาหรือลู
ออกโดยใชทฤษฎีบทเกียวกับลิมตได จึงตองใชวิธีอื่นพิจารณา เชน การพิจารณาคาของ an
่ ิ
โดยตรง หรือจากกราฟของลําดับ an เปนตน
10. จากบทนิยามของอนุกรมจะเห็นวา อนุกรมไดจากการบวกพจนทุกพจนของลําดับ
และในการศึกษาเรื่องลิมิตของอนุกรมไดแบงอนุกรมออกเปน 2 ประเภท เชนเดียวกับลําดับ คือ
อนุกรมลูเขาและอนุกรมลูออก จากตัวอยางของอนุกรมลูเขาจะเห็นวา อนุกรมลูเขามักจะไดจาก
ลําดับลูเขา บางคนอาจจะเขาใจอยางไมถูกตองวา ลําดับลูเขาทุกลําดับเมื่อนํามาเขียนเปนอนุกรม
จะไดอนุกรมลูเขาเสมอ ซึ่งเปนขอที่ควรระวังอยางยิ่งดังตัวอยางตอไปนี้
(1) 1, 1, 1, ..., 1, ... เปนลําดับลูเขาที่มีลิมิตเปน 1
1 + 1 + 1 + ... + 1 + ... เปนอนุกรมลูออก
1
(2) 1, 1 , 1 , ..., , ... เปนลําดับลูเขาที่มีลิมิตเปน 0
2 4 2n −1
1 1 1
1 + + + ... +
n −1
+ ... เปนอนุกรมลูเขา และผลบวกของ
2 4 2
อนุกรมนี้มีคาเปน 2

1 1 1
(3)
1, , ,..., ,... เปนลําดับลูเขาที่มีลิมิตเปน 0
2 3 n
1 1 1
1 + + + ... + + ... เปนอนุกรมลูออก

2 3 n
การแสดงวาอนุกรม 1 + 1 + 1 + ... + 1 + ... เปนอนุกรมลูออกนัน จะตองพิสูจนไดวา
้
2 3 n
ลําดับผลบวกยอยไมมีลิมิต แตวิธีการพิสูจนคอนขางยุงยากในทีนี้จะแสดงคาของพจนแรก ๆ บาง
่
พจนของลําดับผลบวกยอยเพื่อใหเห็นวา เมื่อมีจํานวนพจนมากเขาผลบวกยอยจะมากขึ้นไดเรื่อย ๆ
ดังนี้

6. 6
S1 = 1
1
S2 = 1+
2
1 1
S3 = 1+ +
2 3
1 1 1
S4 = 1+ + +
2 3 4
1 1 1 1 1 1
แต 1+ + + > 1+ + +
2 3 4 2 4 4
> 2
ดังนั้น S4 > 2
1 1 1 1 1 1 1
S8 = 1+ + + + + + +
2 3 4 5 6 7 8
1 ⎛1 1⎞ ⎛1 1 1 1⎞
แต 1+ + ⎜ + ⎟ + ⎜ + + + ⎟
2 ⎝3 4⎠ ⎝5 6 7 8⎠
> 1+ 1 + ⎛ 1 + 1 ⎞ + ⎛ 1 + 1 + 1 + 1 ⎞
⎜ ⎟ ⎜ ⎟
2 ⎝ 4 4⎠ ⎝8 8 8 8⎠
> 21
2
ดังนั้น S8 > 2 1
2
1 ⎛1 1⎞ ⎛1 1 1 1⎞
S16 = 1+ + ⎜ + ⎟ + ⎜ + + + ⎟
2 ⎝3 4⎠ ⎝5 6 7 8⎠
⎛1 1 1 1 ⎞ ⎛ 1 1 1 1 ⎞
+⎜ + + + ⎟ + ⎜ + + + ⎟
⎝ 9 10 11 12 ⎠ ⎝ 13 14 15 16 ⎠
1 ⎛1 1⎞ ⎛1 1 1 1⎞
S16 > 1+ + ⎜ + ⎟ + ⎜ + + + ⎟
2 ⎝ 4 4⎠ ⎝8 8 8 8⎠
⎛1 1 1 1 1 1 1 1⎞
+⎜ + + + + + + + ⎟
⎝ 16 16 16 16 16 16 16 16 ⎠
S16 > 3
จะพบวา S4 (ผลบวก 4 พจนแรก) มากกวา 2
1
S8 (ผลบวก 8 พจนแรก) มากกวา 2
2
S16 (ผลบวก 16 พจนแรก) มากกวา 3
1
S32 (ผลบวก 32 พจนแรก) มากกวา 3
2
S64 (ผลบวก 64 พจนแรก) มากกวา 4
และผลบวกยอยจะมีคามากขึ้นเรื่อย ๆ ไปไมมีที่สิ้นสุด
11. จากการศึกษาเรื่องอนุกรมเลขคณิต จะเห็นวาอนุกรมอนันตที่เปนอนุกรมเลขคณิต
สวนมากเปนอนุกรมลูออก จะทําใหบางคนคิดวาอนุกรมอนันตที่เปนอนุกรมเลขคณิตทุกอนุกรม

7. 7
เปนอนุกรมลูออก แตความจริงแลวมีอนุกรมอนันตที่เปนอนุกรมเลขคณิตและเปนอนุกรมลูเขา คือ

อนุกรม 0 + 0 + 0 + ... + 0 + ... ซึ่งเปนอนุกรมเลขคณิตที่มี a1 = 0 และ d = 0 และมีผลบวก
เปน 0
12. ผูสอนควรย้ํากับผูเรียนวาการพิจารณาอนุกรมวาเปนอนุกรมลูเขาหรือลูออกตอง
พิจารณาจากลําดับของผลบวกยอยของอนุกรมเปนหลัก เชน
พิจารณาอนุกรม 1 – 1 + 1 – 1 + ... + (–1)n–1 + ... จะเห็นวาลําดับของผลบวกยอย
ของอนุกรมนีคือ 1, 0, 1, 0, 1, ... ซึ่งเปนลําดับลูออก
้
ดังนั้น อนุกรม 1 – 1 + 1 – 1 + ... + (–1)n–1 + ... จึงเปนอนุกรมลูออก
ผูสอนควรเสนอแนะเพิ่มเติมวา อาจมีบางคนเขียนจัดรูปอนุกรมขางตนใหมดังนี้
1 – 1 + 1 – 1 + ... + (–1)n–1 + ... = (1 – 1) + (1 – 1) + (1 – 1) + ...
ซึ่งจะไดอนุกรม 0 + 0 + 0 + 0 + ... + 0 + ... เปนอนุกรมลูเขา ที่มีผลบวกเปน 0
หรือบางคนอาจเขียนจัดรูปอนุกรมขางตนใหมดังนี้
1 – 1 + 1 – 1 + ... + (–1)n–1 + ... = 1 + (–1 + 1) + (–1 + 1) + (–1 + 1) + ...
ซึ่งจะไดอนุกรม 1 + 0 + 0 + 0 + 0 + ... เปนอนุกรมลูเขา ที่มีผลบวกเปน 1
ผูสอนควรชี้แนะใหผเู รียนเขาใจใหไดวาการเขียนจัดรูปอนุกรมขางตนทั้งสองแบบ
แลวสรุปวา อนุกรม 1 – 1 + 1 – 1 + ... + (–1)n–1 + ... เปนอนุกรมลูเขานั้นไมถูกตอง
13. ในบทเรียนนี้มุงใหพิจารณาอนุกรมอนันตเฉพาะอนุกรมเรขาคณิตหรืออนุกรมที่
อาจจะหาพจนที่ n ของลําดับผลบวกยอยไดไมยากนัก กลาวคือ ถาเปนอนุกรมเรขาคณิตก็
a1
พิจารณาอัตราสวนรวม r และถา r <1 ก็สามารถหาผลบวกจากสูตร S = สวนอนุกรม
1− r
ที่ไมใชอนุกรมเรขาคณิตนัน ใหหาผลบวกโดยการหาลําดับของผลบวกยอยกอน นั่นคือ จะตอง
้
หาพจนที่ n ของลําดับผลบวกยอยนั้น แลวจึงหาลิมิตของลําดับผลบวกยอย
14. ในบทเรียนนี้ไดนําเสนออนุกรมประเภทหนึ่งซึ่งมีความสําคัญและนาสนใจเรียกวา
อนุกรมเทเลสโคป (telescoping series)
อนุกรมเทเลสโคป คือ อนุกรม a1 + a2 + a3 + ... + an + ... ที่สามารถเขียนอยูในรูป
a1 + a2 + a3 + ... + an + ... = (b1 – b2) + (b2 – b3) + (b3 – b4) + ... + (bn – bn+1) + ...
เมื่อ a1 = b1 – b2
a2 = b2 – b3
a3 = b3 – b4
an = bn – bn+1
ดังนั้น a1 + a2 + a3 ... + an = b1 – bn+1

8. 8
ผูสอนควรเนนลักษณะพิเศษของอนุกรมประเภทนี้ใหผเู รียนทราบ ตัวอยางของอนุกรม
เทเลสโคปในหนังสือเรียน ดังเชน
1 1 1 1 ⎛ 1⎞ ⎛1 1⎞ ⎛1 1⎞ ⎛1 1 ⎞
+ + + ... + = ⎜ 1 − ⎟ + ⎜ − ⎟ + ⎜ − ⎟ + ... + ⎜ − ⎟
1⋅ 2 2 ⋅ 3 3 ⋅ 4 n(n + 1) ⎝ 2⎠ ⎝ 2 3⎠ ⎝3 4⎠ ⎝ n n +1⎠
1
= 1−
n +1
3 5 7 2n + 1 ⎛1 1 ⎞ ⎛ 1 1 ⎞ ⎛ 1 1 ⎞
+ + + ... + 2 = ⎜ − ⎟ + ⎜ − ⎟ + ... + ⎜ 2 −
⎜n
⎟
1 ⋅ 4 4 ⋅ 9 9 ⋅ 16 n ( n + 1) ( n + 1) ⎟
2 2
⎝1 4 ⎠ ⎝ 4 9 ⎠ ⎝ ⎠
1
= 1−
( n + 1)
2
15. ผูสอนอาจจะแนะนําสัญลักษณ ∑ ในหัวขอเรื่องสัญลักษณแทนการบวก ไปพรอม
กับหัวขอเรื่องผลบวกของอนุกรมอนันตเลยก็ได หากพิจารณาแลวเห็นวาสอดคลองกับแนว
ทางการจัดการเรียนการสอนที่ปฏิบัติอยู
16. ในหนังสือเรียนหัวขอ 1.2.2 ไดกลาวถึงสมบัติของ ∑ ที่ควรทราบไว สมบัติ
เหลานั้นแสดงใหเห็นจริงไดโดยงาย ผูสอนควรเชิญชวนใหผูเรียนทดลองพิสูจนสมบัติตาง ๆ ดวย
ตนเอง ดังนี้
n
(1) ∑c = nc เมื่อ c เปนคาคงตัว
i =1
n
∑c = c + c + c + ... + c
i =1
n พจน
= nc
n n
(2) ∑ cai = c∑ a i เมื่อ c เปนคาคงตัว
i=1 i =1
n
∑ cai = ca1 + ca2 + ca3 + ... + can
i=1
= c(a1 + a2 + a3 + ... + an)
n
= c∑ a i
i =1
n n n
(3) ∑ (ai + bi ) = ∑ a i + ∑ bi
i =1 i =1 i =1
n
∑ (ai + bi ) = (a1 + b1) + (a2 + b2) + (a3 + b3) + ... + (an + bn)
i =1
= (a1 + a2 + a3 + ... + an) + (b1 + b2 + b3 + ... + bn)
n n
= ∑ a i + ∑ bi
i =1 i =1

9. 9
n n n
ในทํานองเดียวกันจะแสดงไดวา ∑ (ai − bi ) = ∑ ai − ∑ bi
i =1 i =1 i =1
n
17. ในการหาผลบวก ∑ i นอกจากวิธีที่แสดงไวในหนังสือเรียนแลว ยังแสดงไดโดยวิธี
i =1
n n
เดียวกันกับที่ใชหาสูตรของ ∑ i2 หรือ ∑ i3 ดังนี้
i =1 i =1
2 2
เนื่องจาก n – (n – 1) = 2n – 1 -----(1)
(n – 1)2 – (n – 2)2 = 2(n – 1) – 1 -----(2)
(n – 2)2 – (n – 3)2 = 2(n – 2) – 1 -----(3)
32 – 22 = 2(3) – 1 -----(n–2)
22 – 12 = 2(2) – 1 -----(n–1)
12 – 02 = 2(1) – 1 -----(n)
n n
(1) + (2) + (3) + ... + (n) จะได n2 = 2∑ i − ∑1
i=1 i=1
n
= 2∑ i − n
i=1
n n2 + n n(n + 1)
ดังนั้น ∑i = =
i =1 2 2
n n n
หลังจากศึกษาที่มาของสูตร ∑ i , ∑ i , ∑ i แลว ผูสอนอาจถามผูเรียนตอวา
2 3
i =1 i =1 i =1
n n
การหาสูตร ∑ i หรือ ∑ i จะดําเนินการตามวิธีการเดิมไดหรือไม ผูสอนอาจแนะนําให
4 5
i =1 i =1
ผูเรียนเริ่มตนจาก n – (n – 1)5 และ n6 – (n – 1)6 ตามลําดับ
5
18. แบบฝกหัด 1.2 ข ขอ 7 และขอ 9 อาจจะยากเกินไปหากผูเรียนไมสามารถจัดรูปใหม
ได ดังนัน ผูสอนควรใหคาแนะนําเบื้องตนในแตละขอดังนี้
้ ํ
1 1 1
7(1) = −
n ( n + 1) n n +1
1 1⎛ 1 1 ⎞
7(2) = ⎜ − ⎟
( 2n − 1)( 2n + 1) 2 ⎝ 2n − 1 2n + 1 ⎠
1 1⎛ 1 1 ⎞
7(3) = ⎜ n ( n + 1) − ( n + 1)( n + 2 ) ⎟
⎜ ⎟
n ( n + 1)( n + 2 ) 2⎝ ⎠
1 1⎛1 1 ⎞
7(4) = ⎜ − ⎟
n ( n + 2) 2⎝ n n +2⎠
2n + 1 1 1
9(1) = −
n ( n + 1) ( n + 1)
2 2 2
2
n

10. 10
กิจกรรมแสนอแนะ
ลิมิตของลําดับ
กิจกรรมที่ 1
ผูสอนและผูเรียนชวยกันเขียนกราฟของลําดับ an ตอไปนี้บนกระดานดํา หรือใชโปรแกรม
ประเภทตารางทํางาน เชน Microsoft Excel
1
(1) an =
2n
(2) an = 2
(−1)n
(3) an = 1+
n
(4) an = 2n – 1
(5) an = (–1)n+1
จากนั้นชวยกันพิจารณากราฟของลําดับ an เมื่อ n มีคามากขึ้นโดยไมมีที่สิ้นสุด คาของ
พจนที่ n ของลําดับ จะมีคาเขาใกลจํานวนจริงใดหรือไม ซึ่งผูเรียนควรบอกไดวา
สําหรับ ลําดับในขอ (1) คาของพจนที่ n จะเขาใกล 0
ลําดับในขอ (2) คาของพจนที่ n จะเปน 2 เสมอ
ลําดับในขอ (3) คาของพจนที่ n จะเขาใกล 1
ลําดับในขอ (4) คาของพจนที่ n จะมากขึนเรื่อย ๆ
้
ลําดับในขอ (5) คาของพจนที่ n จะเปน 1 เมื่อ n เปนจํานวนคี่ และ
เปน –1 เมื่อ n เปนจํานวนคู
ผูสอนเสนอแนะผูเรียนวาลําดับในขอ (1), (2) และ (3) คาของพจนที่ n จะเขาใกลหรือ
เทากับจํานวนจริงเพียงจํานวนเดียวเทานั้น ในกรณีที่พจนที่ n ของลําดับมีคาเขาใกลหรือเทากับ
จํานวนจริง L เพียงจํานวนเดียวเทานั้น เมื่อ n มีคามากขึ้นโดยไมมีที่สนสุด จะเรียก L วาเปนลิมิต
ิ้
ของลําดับนั้น หรือกลาววาลําดับนั้นมีลิมิตเปน L สวนลําดับที่ไมมีสมบัติเชนนี้จะเปนลําดับที่ไมมี
ลิมิต ผูสอนใหผูเรียนบอกวาลําดับขางตนลําดับใดบางมีลิมิตและลิมตเปนเทาใด ลําดับใดไมมีลิมต
ิ ิ
ซึ่งผูเรียนควรบอกไดวา ลําดับในขอ (1) มีลิมิตเปน 0 ลําดับในขอ (2) มีลิมิตเปน 2 และลําดับใน
ขอ (3) มีลิมิตเปน 1
ผูสอนทบทวนผูเรียนเกี่ยวกับลําดับที่มีลิมิตเรียกวา ลําดับลูเขา สวนลําดับที่ไมมีลิมิต
เรียกวาลําดับลูออก แลวผูสอนใหผูเรียนบอกวาลําดับทั้งหาลําดับขางตน ลําดับใดเปนลําดับลูเขา
และลําดับใดเปนลําดับลูออก ซึ่งผูเรียนควรบอกไดวา ลําดับในขอ (1), (2) และ (3) เปนลําดับลู
เขา ลําดับในขอ (4) และ (5) เปนลําดับลูออก

11. 11
กิจกรรมที่ 2
ผูสอนอาจใชการพับกระดาษแสดงความหมายของลิมิตของลําดับบางลําดับไดดังตอไปนี้
1 1 1 1 1
เชน พิจารณาลําดับ 1, , , , , ,…
2 4 8 16 32
1
1
2
1
4
1
8
1
16
1
32
ผูสอนอธิบายวาถาพับกระดาษตอไปอีก จะไดความยาวของกระดาษนอยลงเรื่อย ๆ จน
เกือบเปน 0 แสดงวา ถา n มีคามากขึ้นโดยไมมีที่สิ้นสุด พจนที่ n ของลําดับจะเขาใกล 0 และ
กลาวไดวา ลิมิตของลําดับขางตนเทากับ 0

อนุกรมอนันต
กิจกรรมที่ 3
ผูสอนอาจประยุกตใชกจกรรมตอไปนี้นําเขาเรื่องอนุกรมอนันตได ใหผูเรียนปฏิบติ
ิ ั
ตามลําดับขั้นและตอบคําถามตอไปนี้
ขั้นที่ 1 ตัดกระดาษขนาด A4 เปนรูปสี่เหลี่ยมผืนผาสามรูปที่เทากัน ดังรูป

12. 12
ขั้นที่ 2 แยกสวนที่หนึ่งไวกองหนึ่ง สวนที่สองไวอีกกองหนึ่ง เก็บสวนที่สามไวในมือ
ขั้นที่ 3 ทําซ้ําขั้นที่ 1 และ 2 กับกระดาษสวนที่สามที่อยูในมือไปเรื่อย ๆ
1. สมมติวากระดาษ A4 มีพื้นที่ 1 ตารางหนวย และสมมติวาสามารถตัดกระดาษซ้ํา
ตอไปไดอีกอยางตอเนื่องไมสิ้นสุด จะมีกระดาษในกองที่หนึ่งเทาไร กองที่สองเทาไร และมี
เหลืออยูในมือเทาไร ใหเขียนผลบวกของเศษสวนทีใชแทนพื้นที่ของกระดาษที่มีอยูในแตละกอง
่
ผูเรียนควรตอบไดวา จะมีกระดาษในกองที่หนึ่งและกองที่สองเทากันคือเทากับ
1 1 1 1
+ + + + ... ตารางหนวย และกระดาษที่อยูในมือจะชิ้นเล็กลงเรื่อย ๆ จนไมสามารถตัด
3 32 33 34
ไดจริง ๆ
2. สมมติวาสามารถตัดกระดาษซ้ําตอไปไดอีกอยางตอเนืองอยางไมสิ้นสุด เศษสวนในขอ 1
่
จะมีอยูอยางจํากัดหรือนับไมถวน และผลบวกของเศษสวนเหลานันหาคาไดหรือไม
้
ผูเรียนควรตอบไดวา เศษสวนในขอ 1 มีอยูอยางไมจํากัด แตผลบวกของเศษสวนเหลานั้น
ยังไมแนใจวาจะหาไดหรือไม
3. อนุกรมอนันต คือ ผลบวกของจํานวนหลาย ๆ จํานวน นับไมถวน เชน 1 + 2 + 3 + 4
+ 5 + ... + n + ... เปนอนุกรมอนันต อนุกรมนี้สามารถหาผลบวกเปนจํานวน ๆ หนึงไดหรือไม
่
ผูเรียนควรตอบไดวา ไมสามารถหาผลบวกดังกลาวได

4. ถาอนุกรมอนันตไมสามารถหาผลบวกเปนจํานวน ๆ หนึ่งได เรียกอนุกรมนั้นวา
1 1 1 1
อนุกรมลูออก เชน อนุกรมในขอ 3 เปนอนุกรมลูออก อนุกรม + + + + ... ลูออก
2 2 2 23 2 4
หรือไม ใหสรางแบบจําลองการตัดกระดาษคลาย ๆ กับที่ทํามาแลว
1 1 1 1
อนุกรม + + + + ... ยังไมแนใจวาจะหาผลบวกไดหรือไม แบบจําลองการ
2 2 2 23 2 4
ตัดกระดาษไปเรื่อย ๆ ซึ่งแทนอนุกรม 1 + 12 + 13 + 14 + ... ในขอ 4 เปนดังนี้
2 2 2 2
1
23 1
24
1
2
1
22

13. 13
กิจกรรมที่ 4
n
การหาสูตร ∑ i นอกจากจะใชวิธีทางพีชคณิตดังที่ปรากฏในหนังสือเรียนแลว ผูสอน
i =1
อาจเพิ่มความนาสนใจใหผูเรียนโดยใชพนที่สรุปการหาผลบวกของ i ไดอีกวิธหนึงดังนี้
ื้ ี ่
กําหนดใหรูปสี่เหลี่ยมจัตุรัสเล็ก ๆ 1 รูป มีพื้นที่ 1 ตารางหนวย
รูปที่ 1
จะเห็นวารูปที่ 1 มีพื้นที่เทากับ 1 + 2 + 3 + 4 ตารางหนวย
ถานํารูปที่ 1 จํานวนสองรูปมาประกอบกัน จะไดรูปสี่เหลี่ยมผืนผาหนึ่งรูป ดังนี้
4
4
4 5
รูปสี่เหลี่ยมผืนผาที่ไดมีพื้นที่เปนสองเทาของรูปที่ 1 และมีพื้นที่เทากับ 4 × 5 ตารางหนวย
ดังนัน จึงได 4 × 5 = 2(1 + 2 + 3 + 4)
้
4×5
= 1+2+3+4
2
ในทํานองเดียวกัน เมื่อ n เปนจํานวนเต็มบวก และตองการหาคาของ 1 + 2 + 3 + ... + n
ก็พิจารณาจากพื้นที่ได
n n
n n+1

14. 14
จะเห็นวารูปซาย มีพื้นที่เทากับ 1 + 2 + 3 + 4 + ... + n ตารางหนวย
ถานํารูปซายจํานวนสองรูปมาประกอบกัน จะไดรูปสี่เหลี่ยมผืนผาหนึ่งรูปทีมความยาว
่ ี
n + 1 หนวย และความกวาง n หนวย
รูปสี่เหลี่ยมผืนผามีพื้นที่เปนสองเทาของรูปซาย และมีพื้นที่เทากับ n(n + 1) ตารางหนวย
ดังนัน จึงได n(n + 1) = 2(1 + 2 + 3 + 4 + ... + n)
้
n
= 2∑ i
i=1
n n(n + 1)
∑i = 2
i =1
ตัวอยางแบบทดสอบประจําบท
1. ลําดับตอไปนี้เปนลําดับลูเขาหรือลูออก
2n 1 − n2
(1) an = (2) an =
5n − 3 2 + 3n 2
n
n2 − n + 7 ⎛9⎞
(3) an = (4) an = 1+ ⎜ ⎟
2n 3 + n 2 ⎝ 10 ⎠
n
⎛ 1⎞
(5) an = 2−⎜− ⎟ (6) an = 1 + (–1)n
⎝ 2⎠
2. จงตัดสินวาลําดับตอไปนี้เปนลําดับลูเขาหรือลูออก โดยพิจารณาคาของพจนตาง ๆ ในลําดับ
โดยตรง หรือใชเครื่องคํานวณชวยเขียนกราฟของลําดับ หรือใชทฤษฎีบทเกี่ยวกับลิมต ิ
n−2 1
(1) an = (2) an = (−1) n +1
n + 13 n
3. เขียน 0.249 ใหอยูในรูปเศษสวน
4. จงหาคา
∞ ∞
(1) ∑ 2 (2) ∑ 4k
1
3
n =1
n
k =1
2
−1
∞ 2n + 7 n ∞
⎛ 6 6 ⎞
(3) ∑ n
(4) ∑ ⎜ 4k − 1 − 4k + 3 ⎟
n =0 9 ⎝
k =1 ⎠
1 1 1 1
5. อนุกรม + + + ... + + ... เปนอนุกรมลูเขาหรือลูออก
1⋅ 5 2 ⋅ 6 3 ⋅ 7 n(n + 4)
6. การเลนบันจีจัมป (bungee jump) เปนกิจกรรมทาทายที่ผูเลนกระโดดลงมาจากที่สงโดยมีปลาย
ู
เชือกดานหนึ่งผูกติดลําตัวหรือหัวเขาของผูเลน ปลายเชือกอีกดานหนึ่งผูกติดไวกบฐานกระโดด
ั
ชายคนหนึงใชเชือกยาว 250 ฟุต กระโดดบันจีจัมปจากฐานกระโดด และพบวาหลังจากใน
่
แตละครั้งที่เขาดิ่งลงถึงตําแหนงต่ําสุด เชือกที่มีความยืดหยุนสูงจะดึงตัวเขาใหลอยขึ้นเปน
ระยะทาง 55% ของระยะทางที่เขาดิ่งลงถึงตําแหนงต่ําสุด จงหาระยะทางที่ชายคนนี้เคลื่อนที่
ลอยขึ้นและดิ่งลงทั้งหมด

15. 15
เฉลยตัวอยางแบบทดสอบประจําบท
2n 2n 2
1. (1) lim
n →∞ 5n − 3
= lim
n →∞ ⎛
= lim
n →∞ 3
3⎞
n⎜5 − ⎟ 5−
⎝ n⎠ n
⎛ 3⎞
เนื่องจาก lim 2
n →∞
= 2 และ lim ⎜ 5 − ⎟
n →∞ ⎝
= 5
n⎠
2 lim 2 2
จะได lim
n →∞ 3
= n →∞ =
5− ⎛ 3⎞ 5
lim 5 − ⎟
n n →∞ ⎜
⎝ n⎠
2n 2n 2
ดังนั้น ลําดับ an = เปนลําดับลูเขา และ lim
n →∞ 5n − 3
=
5n − 3 5
⎛ 1 ⎞ 1
n 2 ⎜ 2 − 1⎟ −1
1− n 2
⎝n ⎠ = lim n 2
(2) lim
n →∞ 2 + 3n 2
= nlim →∞ 2 ⎛ 2 n →∞ 2
⎞ +3
n ⎜ 2 + 3⎟
⎝n ⎠ n2
เนื่องจาก nlim ⎛ 12 − 1⎞ = –1 และ nlim ⎛ 22 + 3 ⎞ = 3
→∞ ⎜ n ⎟ →∞ ⎜ n ⎟
⎝ ⎠ ⎝ ⎠
1 ⎛ 1 ⎞
−1 lim − 1⎟
n →∞ ⎜ n 2
จะได nlim 2 →∞
n2 = ⎝ ⎠ = −1
+3 ⎛ 2 ⎞ 3
lim + 3⎟
n2 n →∞ ⎜ n 2
⎝ ⎠
1 − n2
เปนลําดับลูเขา และ nlim 1 − n 2
2
1
ดังนั้น ลําดับ a n = →∞ 2 + 3n
= −
2 + 3n 2 3
⎛1 1 7 ⎞ 1 1 7
n3 ⎜ − 2 + 3 ⎟ − 2+ 3
n −n+7
2
n n n ⎠
(3) lim
n →∞ 2n 2 + n 2
= nlim ⎝
→∞
= nlim n n 1 n
→∞
3⎛ 1⎞
n ⎜2+ ⎟ 2+
⎝ n⎠ n
เนื่องจาก nlim ⎛ 1 − 13 + 73 ⎞ = 0 และ nlim ⎛ 2 + 1 ⎞ = 2
→∞ ⎜ n n ⎟ →∞ ⎜ ⎟
⎝ n ⎠ ⎝ n⎠
1 1 7
− 2+ 3
จะได nlim n n 1 n = 0 = 0
→∞
2+ 2
n
ดังนั้น ลําดับ a n = 2 2 เปนลําดับลูเขา และ nlim n − n + 27 = 0
n2 − n + 7 2
2n + n →∞ 2n 3 + n
n
⎛ 9⎞
(4) เนื่องจาก lim 1
n →∞
= 1 และ lim
n →∞ ⎜ 10 ⎟
=0
⎝ ⎠
⎛ ⎛ 9 ⎞n ⎞ ⎛9⎞
n
จะได lim ⎜ 1 + ⎜ ⎟ ⎟
n →∞ ⎜ ⎝ 10 ⎠ ⎟
= lim 1 + lim ⎜ ⎟
n →∞ n →∞ ⎝ 10 ⎠
⎝ ⎠
= 1+0
⎛9⎞
n
⎛ ⎛ 9 ⎞n ⎞
ดังนั้น ลําดับ an = 1+ ⎜ ⎟ เปนลําดับลูเขา และ lim ⎜ 1 + ⎟
n →∞ ⎜ ⎜ 10 ⎟ ⎟
=1
⎝ 10 ⎠ ⎝ ⎝ ⎠ ⎠

16. 16
n
⎛ 1⎞
(5) เนื่องจาก lim 2
n →∞
= 2 และ lim −
n →∞ ⎜ 2 ⎟
=0
⎝ ⎠
⎛ ⎛ 1⎞ ⎞
n
⎛ 1⎞
n
จะได lim ⎜ 2 − ⎜ − ⎟ ⎟
n →∞ ⎜
= lim 2 − lim ⎜ − ⎟
⎝ ⎝ 2⎠ ⎟ ⎠
n →∞ n →∞ ⎝ 2 ⎠
= 2–0 = 2
⎛ 1⎞
n
⎛ ⎛ 1⎞ ⎞
n
ดังนั้น an = 2−⎜− ⎟ เปนลําดับลูเขา และ lim ⎜ 2 − ⎜ − ⎟ ⎟
n →∞ ⎜
= 2
⎝ 2⎠ ⎝ ⎝ 2⎠ ⎟ ⎠
(6) ลําดับนี้คือ 0, 2, 0, 2, ... ซึ่งไมมีลิมิต ดังนั้น ลําดับนี้เปนลําดับลูออก
2. (1) พิจารณาคาของ an โดยตรง เมื่อ n มีคามากขึ้น n – 2 และ n +13 มีคาใกลเคียงกัน
n−2
มาก ลิมิตของลําดับ an = จึงเทากับ 1
n + 13
ใชทฤษฎีบทเกี่ยวกับลิมิตเพือสนับสนุนการพิจารณาขางตนดังนี้
่
⎛ 2⎞ 2
n ⎜1 − ⎟ 1−
n−2 ⎝ n⎠
lim
n →∞ n + 13
= nlim →∞ ⎛ 13 ⎞
= nlim 13
→∞
n
n ⎜1 + ⎟ 1+
⎝ n⎠ n
เนื่องจาก nlim ⎛1 − 2 ⎞ = 1 และ nlim ⎛1 + 13 ⎞ = 1
→∞ ⎜ ⎟ →∞ ⎜ ⎟
⎝ n⎠ ⎝ n⎠
2 ⎛ 2⎞
1− lim ⎜1 − ⎟
n →∞ ⎝ n⎠
จะได nlim 13 =
→∞
n
1+ ⎛ 13 ⎞
lim 1 + ⎟
n n →∞ ⎜⎝ n⎠
1
= = 1
1
ดังนั้น ลําดับ a n = n − 2 เปนลําดับลูเขา และ nlim n − 2
→∞ n + 13
=3
n + 13
1 1 1 1 1
(2) คํานวณหาแตละพจนของลําดับ an = (−1) n +1 ไดลําดับ 1, − , , − , , ...
n 2 3 4 5
จากนั้นพิจารณาคาของ an โดยตรง หรือเขียนกราฟของลําดับ an โดยใชโปรแกรม
ประเภทตาราง เชน Microsoft Excel มาชวย จะไดกราฟดังรูป
an
1
0.8
0.6
0.4
0.2
0
2 4 6 8 10
n
-0.2
-0.4

17. 17
จากกราฟ จะเห็นวา an จะเขาใกล 0 เมื่อ n มีคามากขึ้นโดยไมมีที่สนสุด
ิ้
ดังนั้น ลําดับ an = (−1) n +1
1
เปนลําดับลูเขา และ n →∞ ⎛ (−1)n +1 1 ⎞ = 0
lim ⎜ ⎟
n ⎝ n⎠
3. 0.249 = 0.24999...
= 0.24 + 0.009 + 0.0009 + 0.00009 + ...
9 9 9
= 0.24 + 3
+ 4 + 5 + ...
10 10 10
9 9 9 9
3
+ 4 + 5 + ... เปนอนุกรมเรขาคณิตที่มี a1 = 3
และ r = 1
10 10 10 10 10
1 9 9 9
เนื่องจาก r = <1 อนุกรม 3 + 4 + 5 + ... เปนอนุกรมลูเขา
10 10 10 10
9 9
a1 103 103 = 1
และมีผลบวกเทากับ = 1
= 9 = 0.01
1− r 1− 100
10 10
1
ดังนั้น 0.249 = 0.24 + 0.01 = 0.25 =
4
∞
4. (1) ∑ 2 = n
2 2 2 2
+ 2 + 3 + ... + n + ...
3 n =1 3 3 3 3
2 1
เปนอนุกรมเรขาคณิตที่มี a1 = และ r =
3 3
1 1
เนื่องจาก r = = < 1 อนุกรมนี้เปนอนุกรมลูเขา
3 3
2
a1
และมีผลบวกเทากับ = 3
1
= 1
1− r 1−
3
∞
ดังนั้น ∑ 2 = 1 n
3 n =1
n
(2) ให Sn = ∑ 1
4k − 1 k =1
2
1 1
เนื่องจาก =
4k − 1 2
(2k) 2 − 1
1
=
(2k − 1)(2k + 1)
n ⎛1
⎛ 1 1 ⎞⎞
จะได Sn = ∑ ⎜ 2 ⎜ 2k − 1 − 2k + 1 ⎟ ⎟
k =1⎝ ⎝ ⎠ ⎠
1 n ⎛ 1 1 ⎞
= ∑ ⎝ 2k − 1 − 2k + 1 ⎠
⎜ ⎟
2 k =1
1 ⎛⎛ 1 ⎞ ⎛ 1 1 ⎞ ⎛ 1 1 ⎞ ⎛ 1 1 ⎞⎞
= ⎜ ⎜1 − ⎟ + ⎜ − ⎟ + ⎜ − ⎟ + ... + ⎜ − ⎟⎟
2 ⎝⎝ 3 ⎠ ⎝ 3 5 ⎠ ⎝ 5 7 ⎠ ⎝ 2n − 1 2n + 1 ⎠ ⎠

18. 18
1⎛ 1 ⎞
= ⎜1 − ⎟
2 ⎝ 2n + 1 ⎠
1⎛ 1 ⎞ 1
lim Sn
n →∞
= lim ⎜ 1 −
n →∞ 2 ⎝ ⎟ =
2n + 1 ⎠ 2
∞
ดังนั้น ∑ 1 = 1
4k − 1
k =1
2
2
∞ 2n + 7 n ∞ 2n ∞ n
(3) ∑ = ∑ + ∑7
n =0 9n n =0 9
n
9
n =0
n
∞ ⎛ 2 ⎞n ∞ ⎛ 7 ⎞n
= ∑⎜ ⎟ + ∑⎜ ⎟
n =0 ⎝ 9 ⎠ ⎝9⎠
n =0
1 1
= 2
+ 7
1− 1−
9 9
9 9 18 + 63 81
= + = =
7 2 14 14
∞ 2n + 7 n 81
∑ =
n =0 9n 14
(4) ให Sn = ∑ ⎛ 6 − 6 ⎞
n
⎜ ⎟
⎝ 4k − 1 4k + 3 ⎠
k =1
n
⎛ 6 6 ⎞
จะได Sn = ∑ ⎝ 4k − 1 − 4k + 3 ⎠
⎜ ⎟
k =1
⎛ 6⎞ ⎛6 6 ⎞ ⎛ 6 6 ⎞ ⎛ 6 6 ⎞
= ⎜ 2 − ⎟ + ⎜ − ⎟ + ⎜ − ⎟ + ... + ⎜ − ⎟
⎝ 7 ⎠ ⎝ 7 11 ⎠ ⎝ 11 15 ⎠ ⎝ 4n − 1 4n + 3 ⎠
6
= 2−
4n + 3
⎛ 6 ⎞
lim S
n →∞ n
= lim 2 −
n →∞ ⎜ ⎟ = 2
⎝ 4n + 3 ⎠
∞
ดังนั้น ∑ ⎛ 6 − 6 ⎞ = 2
⎜ ⎟
k =1⎝ 4k − 1 4k + 3 ⎠
1 1⎛1 1 ⎞
5. พิจารณา = ⎜ − ⎟
k(k + 4) 4⎝k k+4⎠
1 1 1 1
ดังนั้น Sn = + + + ... +
1⋅ 5 2⋅6 3⋅ 7 n(n + 4)
1 ⎛⎛ 1⎞ ⎛1 1⎞ ⎛1 1⎞ ⎛1 1⎞ ⎛1 1⎞ ⎛1 1 ⎞
= ⎜ ⎜1 − ⎟ + ⎜ − ⎟ + ⎜ − ⎟ + ⎜ − ⎟ + ⎜ − ⎟ + ⎜ − ⎟ +
4 ⎝ ⎝ 5 ⎠ ⎝ 2 6 ⎠ ⎝ 3 7 ⎠ ⎝ 4 8 ⎠ ⎝ 5 9 ⎠ ⎝ 6 10 ⎠
⎛1 1 ⎞ ⎛1 1 ⎞⎞
⎜ − ⎟ + ... + ⎜ − ⎟⎟
⎝ 7 11 ⎠ ⎝ n n + 4 ⎠⎠
1⎛ 1 1 1⎞ 1⎛ 1 1 1 1 ⎞
= ⎜1 + + + ⎟ + ⎜ − − − − ⎟
4 ⎝ 2 3 4 ⎠ 4 ⎝ n +1 n + 2 n + 3 n + 4 ⎠

19. 19
⎛1⎛ 1 1 1⎞ 1⎛ 1 1 1 1 ⎞⎞
เนื่องจาก lim Sn
n →∞
= lim ⎜ ⎜ 1 + + + ⎟ + ⎜ − − − − ⎟⎟
⎝ ⎝ 2 3 4 ⎠ 4 ⎝ n +1 n + 2 n + 3 n + 4 ⎠⎠
n →∞ 4
1⎛ 1 1 1⎞
= ⎜1 + + + ⎟
4⎝ 2 3 4⎠
25
=
48
1 1 1 1 25
ดังนั้น อนุกรม + + + ... + + ... เปนอนุกรมลูเขา และมีผลบวกเทากับ
1⋅ 5 2⋅6 3⋅ 7 n(n + 4) 48
6. ระยะทางทีชายคนนี้เริ่มกระโดดจนถึงตําแหนงต่ําสุดมีระยะทาง 250 ฟุต
่
ชายคนนี้จะลอยขึ้นสูงเปนระยะทาง 55% ของระยะทางที่เขาดิ่งลงถึงตําแหนงต่ําสุด
มีคาเทากับ 11 ของระยะทางที่เขาดิ่งลงถึงตําแหนงต่ําสุด
20
ระยะทางที่ชายคนนี้ลอยขึ้นครั้งที่ 1 แลวดิ่งลงถึงตําแหนงต่ําสุดมีระยะทาง
11 11 11
คือ 250 ⎛ 20 ⎞ + 250 ⎛ 20 ⎞ = 500 ⎛ 20 ⎞ ฟุต
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
ระยะทางที่ชายคนนี้ลอยขึ้นครั้งที่ 2 แลวดิ่งลงถึงตําแหนงต่ําสุดมีระยะทางคือ
11 11 11 11 11 2
250 ⎛ 20 ⎞⎛ 20 ⎞ + 250 ⎛ 20 ⎞⎛ 20 ⎞ = 500 ⎛ 20 ⎞
⎜ ⎟⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎜ ⎟ ฟุต
⎝ ⎠⎝ ⎠ ⎝ ⎠⎝ ⎠ ⎝ ⎠
ระยะทางที่ชายคนนี้ลอยขึ้นแลวดิ่งลงเปนเชนนีไปเรื่อย ๆ
้
จะไดระยะทางที่ชายคนนี้เคลื่อนที่ลอยขึ้นและดิ่งลงทั้งหมดเทากับ
2 3
⎛ 11 ⎞ ⎛ 11 ⎞ ⎛ 11 ⎞
250 + 500 ⎜ ⎟ + 500 ⎜ ⎟ + 500 ⎜ ⎟ + ...
⎝ 20 ⎠ ⎝ 20 ⎠ ⎝ 20 ⎠
⎛ 11 ⎛ 11 ⎞2 ⎛ 11 ⎞3 ⎞
= 250 + 500 ⎜ + ⎜ ⎟ + ⎜ ⎟ + ... ⎟
⎜ 20 ⎝ 20 ⎠ ⎝ 20 ⎠ ⎟
⎝ ⎠
⎛ 11 ⎞
⎜ ⎟
= 250 + 500 ⎜ 20 ⎟
11
⎜1− ⎟
⎜ ⎟
⎝ 20 ⎠
⎛ 11 ⎞
= 250 + 500 ⎜ ⎟
⎝9⎠
= 861.11
ดังนั้น ในการกระโดดบันจีจัมปครั้งนี้ ชายคนนี้เคลื่อนที่ลอยขึ้นและดิ่งลงเปนระยะทาง
ทั้งหมด 861.11 ฟุต

20. 20
เฉลยแบบฝกหัด 1.1 ก
1. (1) a2 = a1 + 2 – 1 = 0 + 2 – 1 = 1
a3 = a2 + 3 – 1 = 1 + 3 – 1 = 3
a4 = a3 + 4 – 1 = 3 + 4 – 1 = 6
a5 = a4 + 5 – 1 = 6 + 5 – 1 = 10
ดังนั้น 5 พจนแรกของลําดับนี้คือ 0, 1, 3, 6, 10
(2) a2 = 1 + 0.05a1 = 1 + 0.05(1000) = 51
a3 = 1 + 0.05a2 = 1 + 0.05(51) = 3.55
a4 = 1 + 0.05a3 = 1 + 0.05(3.55) = 1.1775
a5 = 1 + 0.05a4 = 1 + 0.05(1.1775) = 1.058875
ดังนั้น 5 พจนแรกของลําดับนี้คือ 1000, 51, 3.55, 1.1775, 1.058875
(3) a2 = 6a1 = 6(2) = 12
a3 = 6a2 = 6(12) = 72
a4 = 6a3 = 6(72) = 432
a5 = 6a4 = 6(432) = 2592
ดังนั้น 5 พจนแรกของลําดับนี้คือ 2, 12, 72, 432, 2592
(4) a3 = a2 + 2a1 = 2 + 2(1) = 4
a4 = a3 + 2a2 = 4 + 2(2) = 8
a5 = a4 + 2a3 = 8 + 2(4) = 16
ดังนั้น 5 พจนแรกของลําดับนี้คือ 1, 2, 4, 8, 16
(5) a3 = a2 + a1 = 0+2 = 2
a4 = a3 + a2 = 2+0 = 2
a5 = a4 + a3 = 2+2 = 4
ดังนั้น 5 พจนแรกของลําดับนี้คือ 2, 0, 2, 2, 4
2. (1) เปนลําดับเลขคณิต มีผลตางรวมเปน 2
(2) เปนลําดับเรขาคณิต มีอัตราสวนรวมเปน –1
(3) เปนลําดับเลขคณิต มีผลตางรวมเปน –2
1
(4) เปนลําดับเรขาคณิต มีอัตราสวนรวมเปน
3
(5) ไมเปนทั้งลําดับเลขคณิตและลําดับเรขาคณิต

21. 21
3. (1) d = 4 – (–2) = 6
เนื่องจาก an = a1 + (n – 1)d
∴ an = –2 + (n – 1)6
= 6n – 8
พจนที่ n ของลําดับนี้คือ an = 6n – 8
1 ⎛ 1⎞ 1
(2) d = −⎜− ⎟ =
6 ⎝ 6⎠ 3
เนื่องจาก an = a1 + (n – 1)d
1 1
∴ an = − + (n − 1)
6 3
3 n
= − +
6 3
2n − 3
=
6
2n − 3
พจนที่ n ของลําดับนี้คือ an =
6
1 5
(3) d = 13 − 11 =
2 2
เนื่องจาก an = a1 + (n – 1)d
5
∴ an = 11 + (n − 1)
2
17 5n
= +
2 2
5n + 17
=
2
5n + 17
พจนที่ n ของลําดับนี้คือ an =
2
(4) d = 22.54 – 19.74 = 2.8
เนื่องจาก an = a1 + (n – 1)d
∴ an = 19.74 + (n – 1)(2.8)
= 2.8n + 16.94
พจนที่ n ของลําดับนี้คือ an = 2.8n + 16.94
(5) d = (x + 2) – x = 2
เนื่องจาก an = a1 + (n – 1)d
∴ an = x + (n – 1)2
= x + 2n – 2
พจนที่ n ของลําดับนี้คือ an = x – 2 + 2n

22. 22
(6) d = (2a + 4b) – (3a + 2b) = –a + 2b
เนื่องจาก an = a1 + (n – 1)d
∴ an = (3a + 2b) + (n – 1)(–a + 2b)
= 3a + 2b – na + 2nb + a – 2b
= 4a – na + 2nb
พจนที่ n ของลําดับนี้คือ an = 4a – na + 2nb
4. จะได 5p – p = 6p + 9 – 5p
4p = p+9
3p = 9
p = 3
จะได สามพจนแรกของลําดับนี้คือ 3, 15, 27 ลําดับนี้มีผลตางรวมเปน 12
ดังนั้น สี่พจนตอไปของลําดับนี้คือ 39, 51, 63, 75
5. ใหลําดับนี้มีสามพจนแรกคือ a – d, a, a + d
จะได a–d+a+a+d = 12 ---------- (1)
3 3 3
และ (a – d) + a + (a + d) = 408 ---------- (2)
จาก (1) 3a = 12
a = 4
จาก (2), a3 – 3a2d + 3ad2 – d3 + a3 + a3 + 3a2d + 3ad2 + d3 = 408
3a3 + 6ad2 = 408
3 2
3(4) + 24d = 408
24d2 = 408 – 192
216
d2 =
24
= 9
d = 3 หรือ –3
ถา d = 3 แลว จะไดลําดับนี้คือ 1, 4, 7, 10, 13, ...
ถา d = –3 แลว จะไดลําดับนี้คือ 7, 4, 1, –2, –5, ...
−6
6. (1) r = = 2
−3
เนื่องจาก an = a1rn–1
∴ an = (–3)2n–1
พจนที่ n ของลําดับนี้คือ an = (–3)2n–1

23. 23
−5 1
(2) r = = −
10 2
เนื่องจาก an = a1rn–1
n −1
⎛ 1⎞
∴ an = 10 ⎜ − ⎟
⎝ 2⎠
n −1
⎛ 1⎞
พจนที่ n ของลําดับนี้คือ an = 10 ⎜ − ⎟
⎝ 2⎠
5
(3) r = 4
1
= 5
4
เนื่องจาก an = a1rn–1
⎛ 1 ⎞ n −1
∴ an = ⎜ ⎟5
⎝4⎠
⎛ 1 ⎞ n −1
พจนที่ n ของลําดับนี้คือ an = ⎜ ⎟5
⎝4⎠
5
(4) r = 3
5
= 2
6
เนื่องจาก an = a1rn–1
⎛ 5 ⎞ n −1
∴ an = ⎜ ⎟ (2)
⎝6⎠
⎛ 5 ⎞ n −1
พจนที่ n ของลําดับนี้คือ an = ⎜ ⎟ (2)
⎝6⎠
1
3
(5) r = 12
2
= −
− 8
9
เนื่องจาก an = a1rn–1
n −1
⎛ 2 ⎞⎛ 3 ⎞
∴ an = ⎜ − ⎟⎜ − ⎟
⎝ 9 ⎠⎝ 8 ⎠
n −1
⎛ 2 ⎞⎛ 3 ⎞
พจนที่ n ของลําดับนี้คือ an = ⎜ − ⎟⎜ − ⎟
⎝ 9 ⎠⎝ 8 ⎠
a 2 b2 a
(6) r = =
ab3 b
เนื่องจาก an = a1rn–1
n −1
⎛a⎞
∴ an = 3
(ab ) ⎜ ⎟
⎝b⎠

24. 24
an
=
b4− n
an
พจนที่ n ของลําดับนี้คือ an =
b4− n
7. (1) ให a1 = –15 และ a5 = –1215
จะได a5 = a 1r4 = –1215
–15r4 = –1215
r4 = 81
r = –3 หรือ r = 3
ดังนั้น สามพจนที่อยูระหวาง –15 กับ –1215 คือ 45, –135, 405 หรือ –45, –135, –405
4 27
(2) ให a1 = และ a5 =
3 64
27
จะได a5 = a 1r4 =
64
4 4 27
r =
3 64
4 81
r =
256
3 3
r = หรือ r = −
4 4
4 27 3 9 3
ดังนั้น 3 พจนที่อยูระหวาง กับ คือ 1, , หรือ –1, , −9
3 64 4 16 4 16
8. ให a เปนจํานวนทีนําไปบวก
่
จะได 3 + a, 20 + a, 105 + a เปนลําดับเรขาคณิต
20 + a 105 + a
ดังนั้น =
3+ a 20 + a
400 + 40a + a2 = 315 + 108a + a2
68a = 85
85 5
a = =
68 4
5
จํานวนที่นําไปบวกคือ
4

25. 25
เฉลยแบบฝกหัด 1.1 ข
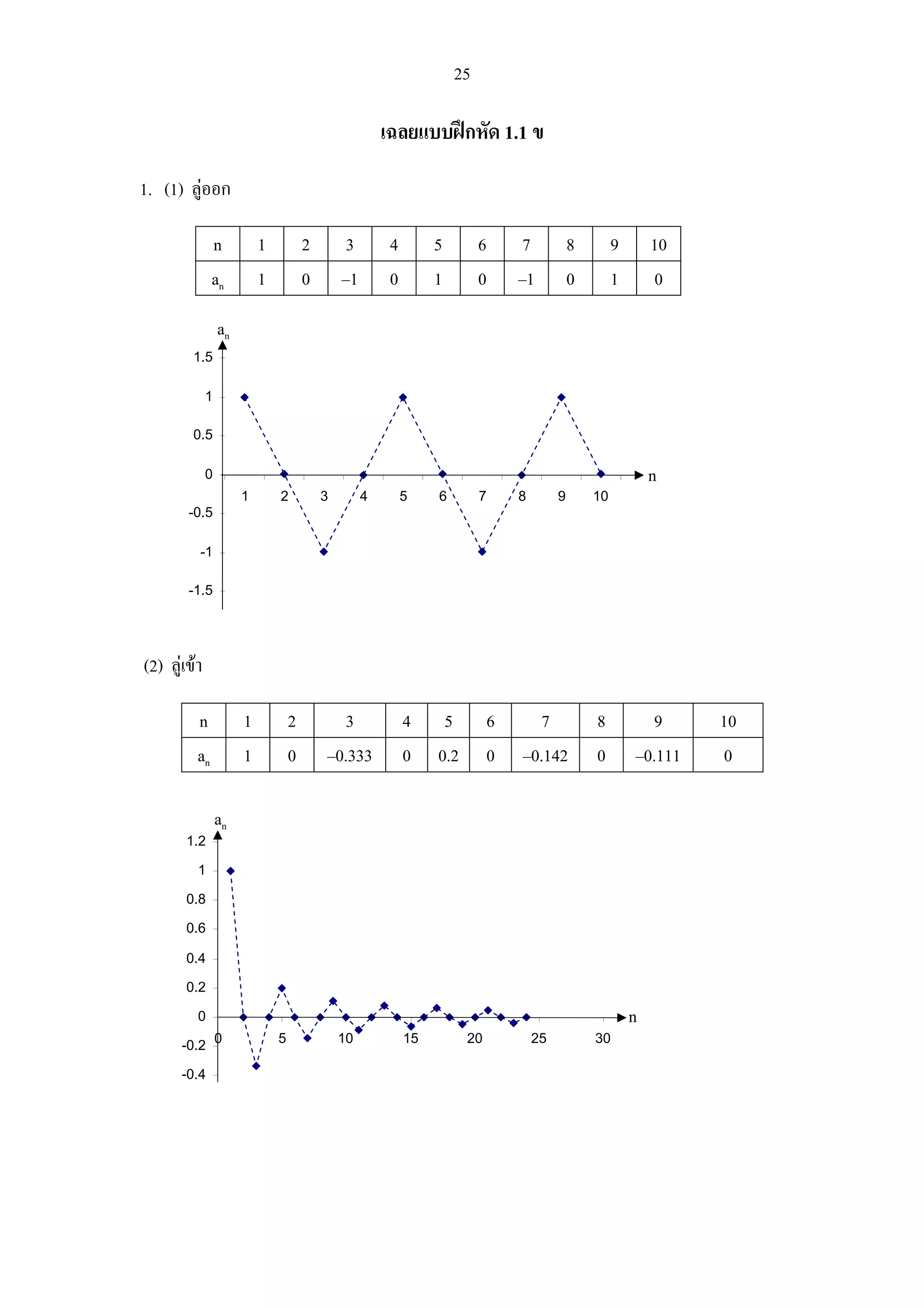
1. (1) ลูออก
n 1 2 3 4 5 6 7 8 9 10
an 1 0 –1 0 1 0 –1 0 1 0
an
1.5
1
0.5
0 n
1 2 3 4 5 6 7 8 9 10
-0.5
-1
-1.5
(2) ลูเขา
n 1 2 3 4 5 6 7 8 9 10
an 1 0 –0.333 0 0.2 0 –0.142 0 –0.111 0
an
1.2
1
0.8
0.6
0.4
0.2
0 n
-0.2 0 5 10 15 20 25 30
-0.4

26. 26
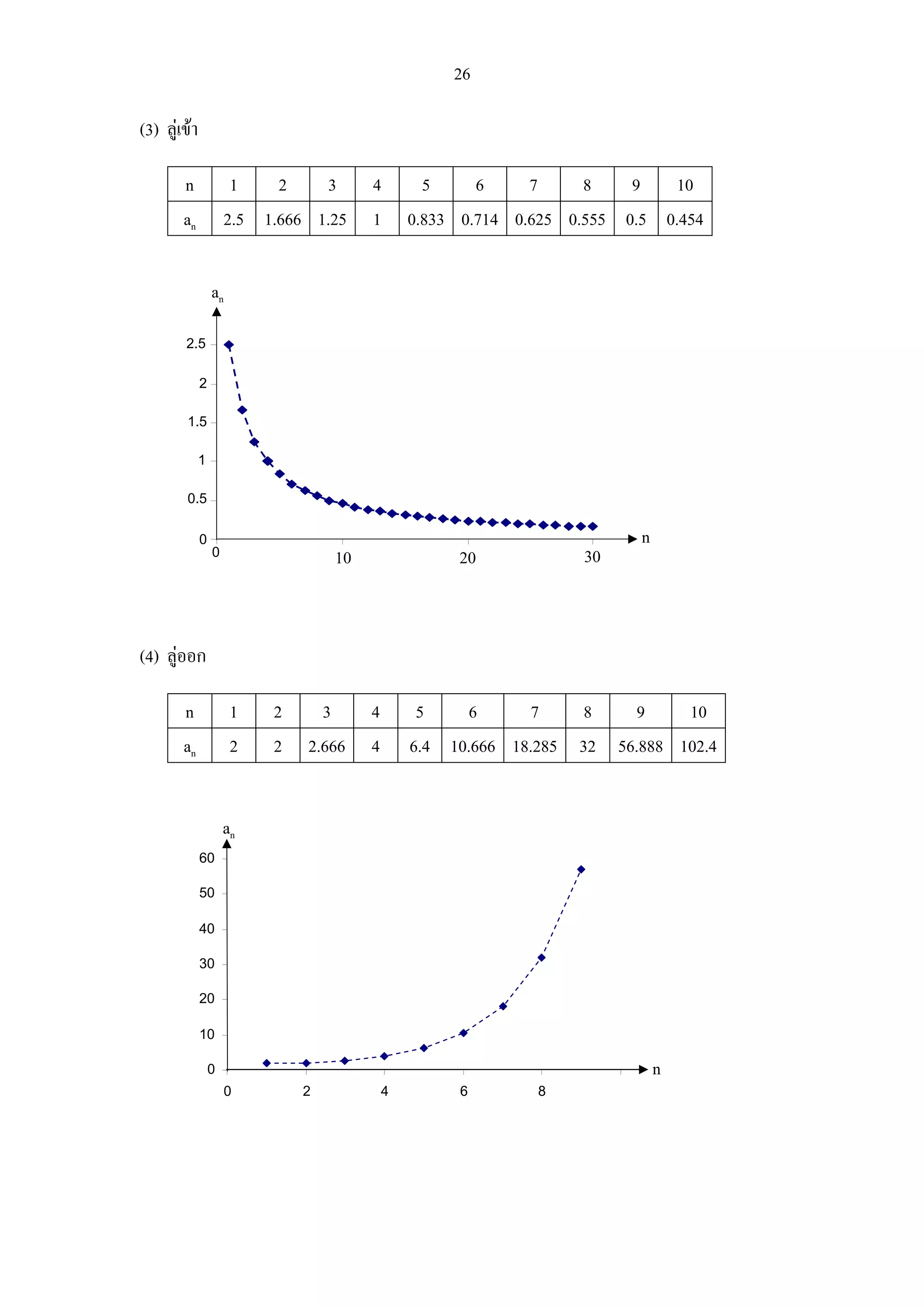
(3) ลูเขา
n 1 2 3 4 5 6 7 8 9 10
an 2.5 1.666 1.25 1 0.833 0.714 0.625 0.555 0.5 0.454
an
2.5
2
1.5
1
0.5
0 n
0 10 20 30
(4) ลูออก
n 1 2 3 4 5 6 7 8 9 10
an 2 2 2.666 4 6.4 10.666 18.285 32 56.888 102.4
an
60
50
40
30
20
10
0 n
0 2 4 6 8

27. 27
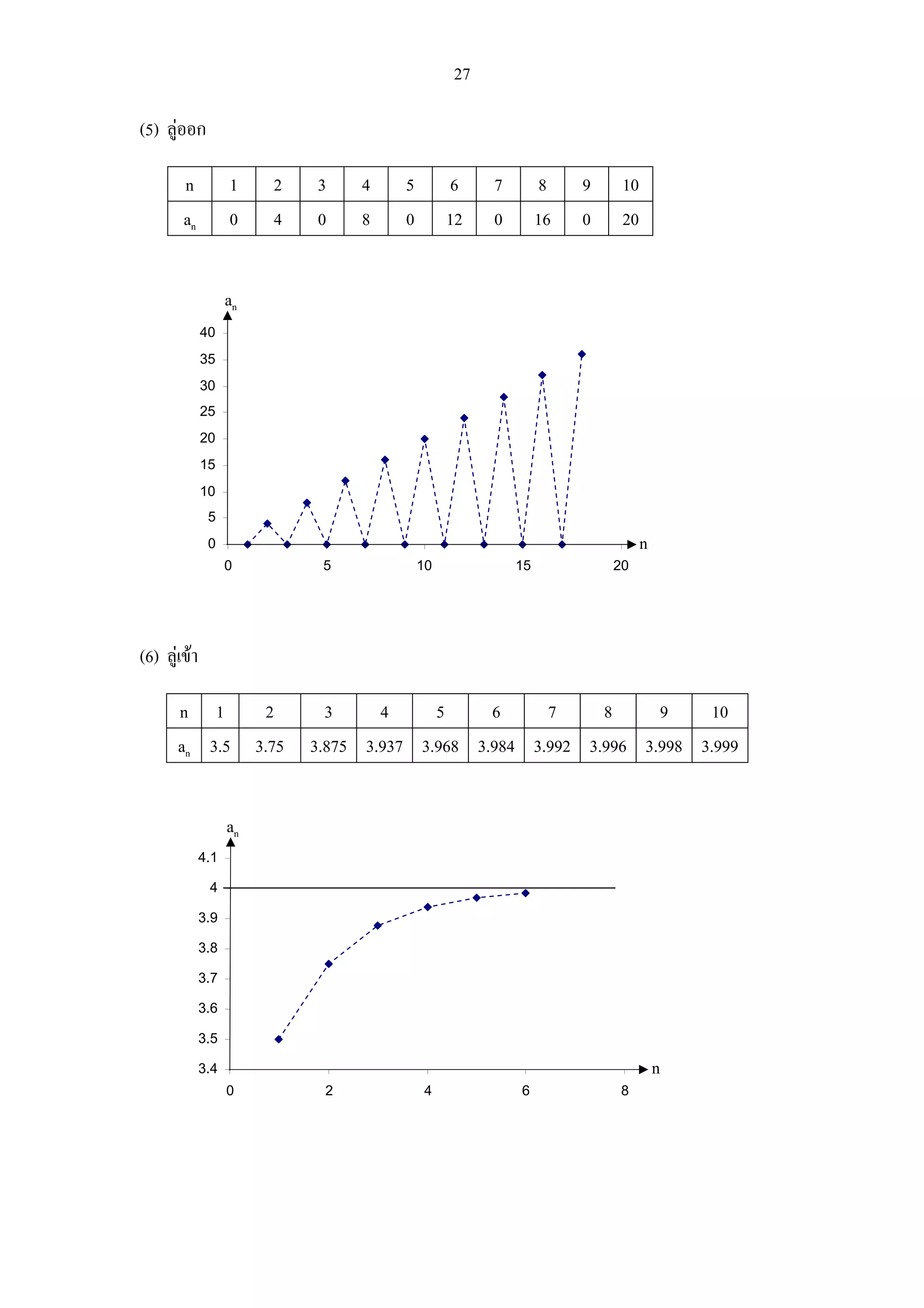
(5) ลูออก
n 1 2 3 4 5 6 7 8 9 10
an 0 4 0 8 0 12 0 16 0 20
an
40
35
30
25
20
15
10
5
0 n
0 5 10 15 20
(6) ลูเขา
n 1 2 3 4 5 6 7 8 9 10
an 3.5 3.75 3.875 3.937 3.968 3.984 3.992 3.996 3.998 3.999
an
4.1
4
3.9
3.8
3.7
3.6
3.5
3.4 n
0 2 4 6 8

28. 28
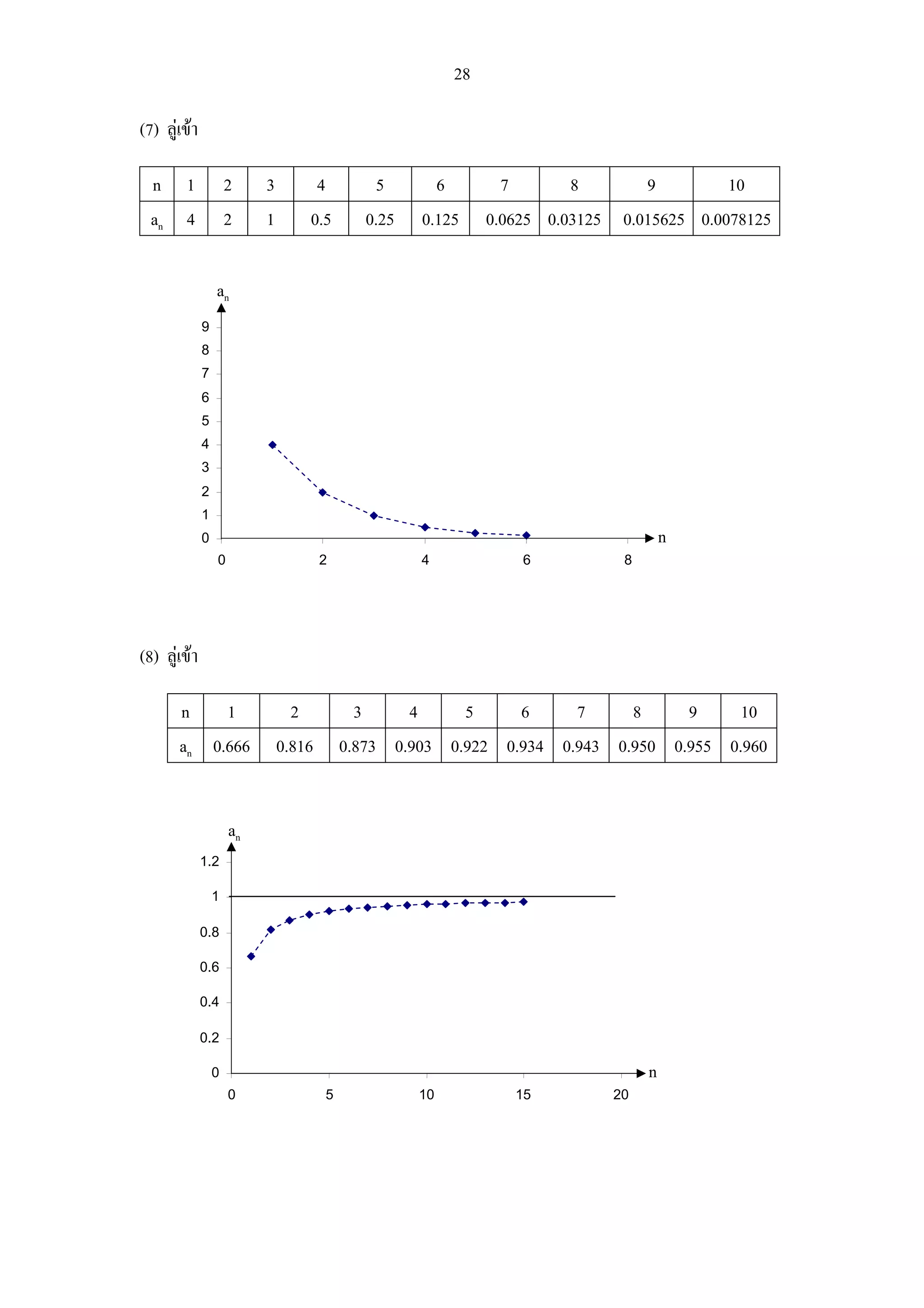
(7) ลูเขา
n 1 2 3 4 5 6 7 8 9 10
an 4 2 1 0.5 0.25 0.125 0.0625 0.03125 0.015625 0.0078125
an
9
8
7
6
5
4
3
2
1
0 n
0 2 4 6 8
(8) ลูเขา
n 1 2 3 4 5 6 7 8 9 10
an 0.666 0.816 0.873 0.903 0.922 0.934 0.943 0.950 0.955 0.960
an
1.2
1
0.8
0.6
0.4
0.2
0 n
0 5 10 15 20

29. 29
(9) ลูออก
n 1 2 3 4 5 6 7 8 9 10
an –1.333 1.777 –2.370 3.160 –4.213 5.618 –7.491 9.988 –13.318 17.757
an
20
15
10
5
0 n
0 2 4 6 8 10 12
-5
-10
-15
(10) ลูเขา
.n 1 2 3 4 5 6 7 8 9 10
an 0.25 0.333 0.3 0.222 0.147 0.090 0.053 0.031 0.017 0.009
an
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0 n
0 2 4 6 8 10 12

30. 30
2. ไมเห็นดวย เพราะเปนการสรุปที่ไมถูกตอง ถา x n และ yn เปนลําดับ การที่จะกลาววา
⎛x ⎞ lim x n
lim ⎜ n ⎟
n →∞ y
= n →∞
ไดนน ขอตกลงเบืองตนเกียวกับ
ั้ ้ ่ lim x n และ lim y n ตองเปน
⎝ n⎠ lim y n n →∞ n →∞
n →∞
จริงกอน ขอกําหนดเบื้องตนนั้นคือ lim x n
n →∞
และ lim y n
n →∞
ตองหาคาได
ในกรณีน้ี ตองจัดรูป an และ bn กอนการใชทฤษฎีบทเกี่ยวกับลิมิต ดังนี้
1 1
n 4 (2 − ) 2−
2n 4 − n 2 n2 n2
จาก = =
3n 4 + 13 n 4 (3 +
13
) 3+
13
n4 n4
1
และเนื่องจาก lim(2 − ) = 2 และ lim(3 + 13 ) = 3
n →∞ n2 n →∞n4
1
2−
ดังนั้น lim
2n 4 − n 2
= lim n2
n →∞ 3n 4 + 13 n →∞ 13
3+
n4
1
lim(2 − )
= n →∞ n2
13
lim(3 + 4 )
n →∞ n
2
=
3
8 8 1
3. (1) lim = lim
n →∞ 3n 3 n →∞ n
8
= (0)
3
= 0
8
ดังนั้น ลําดับ an = เปนลําดับลูเขา
3n
n
8n ⎛8⎞
(2) จาก = ⎜ ⎟
7n ⎝7⎠
n
8n ⎛8⎞
จะได lim
n →∞ 7 n
= lim ⎜ ⎟
n →∞ 7
⎝ ⎠
n
⎛8⎞ 8
lim ⎜ ⎟ หาคาไมได เพราะ >1
n →∞ 7
⎝ ⎠ 7
8n
ดังนั้น ลําดับ an = เปนลําดับลูออก
7n
(3) (−1) n = 1 เมื่อ n เปนจํานวนคู และ (−1) = –1 เมื่อ n เปนจํานวนคี่
n
ดังนั้น ลําดับ an = (–1)n ไมมีลิมิต และเปนลําดับลูออก

31. 31
n n
⎛1⎞ ⎛1⎞
(4) lim 3 ⎜ ⎟ = 3lim ⎜ ⎟
n →∞
⎝2⎠ n →∞ 2
⎝ ⎠
= 3(0)
= 0
n
⎛1⎞
ดังนั้น ลําดับ an = 3⎜ ⎟ เปนลําดับลูเขา
⎝2⎠
1
(5) เนื่องจาก lim 4 = 4 และ lim =0
n →∞ n →∞ n
⎛ 1⎞ 1
จะได lim ⎜ 4 + ⎟ = lim 4 + lim
n →∞
⎝ n⎠ n →∞ n →∞ n
= 4+0
= 4
1
ดังนั้น ลําดับ an = 4+ เปนลําดับลูเขา
n
6n − 4 6n 4 2
(6) จาก = − = 1–
6n 6n 6n 3n
⎛ 2 ⎞
และเนื่องจาก lim1 = 1 และ lim ⎜ ⎟ = 0
n →∞ 3n
n →∞
⎝ ⎠
⎛ 6n − 4 ⎞ ⎛ 2 ⎞
จะได lim ⎜ ⎟ = lim ⎜1 − ⎟
n →∞
⎝ 6n ⎠ n →∞
⎝ 3n ⎠
2
= lim1 − lim
n →∞ n →∞ 3n
= 1–0
= 1
6n − 4
ดังนั้น ลําดับ an = เปนลําดับลูเขา
6n
(7) เมื่อ n มีคาเพิ่มขึ้น คาของพจนที่ n ของลําดับนี้จะเพิ่มขึ้น และไมเขาใกลจํานวนใด
จํานวนหนึ่ง
3n + 5
ดังนั้น ลําดับ an = เปนลําดับลูออก
6
n n 1
(8) จาก = =
n +1 ⎛ 1⎞
1+
1
n ⎜1 + ⎟
⎝ n⎠ n
1
และเนื่องจาก lim1 = 1 และ lim = 0
n →∞ n →∞ n
⎛ ⎞
⎛ n ⎞ ⎜ 1 ⎟
จะได lim ⎜ ⎟ = lim ⎜ ⎟
⎜1+ 1 ⎟
n →∞ n + 1
⎝ ⎠ n →∞
⎜ ⎟
⎝ n⎠

32. 32
lim1
= n →∞
1
lim1 + lim
n →∞ n →∞ n
1
=
1+ 0
= 1
n
ดังนั้น ลําดับ an = เปนลําดับลูเขา
n +1
4
(9) เนื่องจาก lim = 0 และ nlim 5n = 0
n →∞ n2 →∞ n 2
⎛ 4 + 5n ⎞ 4 5n
จะได lim ⎜ 2 ⎟ = lim 2
+ lim 2
n →∞
⎝ n ⎠ n →∞ n n →∞ n
= 0+0
= 0
4 + 5n
ดังนั้น ลําดับ an = เปนลําดับลูเขา
n2
⎛ 1⎞ 1
n⎜2 −⎟ 2−
2n − 1 ⎝ n⎠
(10) จาก = = n
1
3n + 1 ⎛ 1⎞ 3+
n ⎜3 + ⎟
⎝ n⎠ n
⎛ 1⎞ ⎛ 1⎞
และเนื่องจาก lim ⎜ 2 − ⎟ = 2
n →∞ ⎝
และ lim 3 + ⎟
n →∞ ⎜
= 3
n⎠ ⎝ n⎠
⎛ 1⎞
lim ⎜ 2 − ⎟
2n − 1 n →∞
⎝ n⎠
จะได lim =
n →∞ 3n + 1 ⎛ 1⎞
lim ⎜ 3 + ⎟
n →∞
⎝ n⎠
2
=
3
2n − 1
ดังนั้น ลําดับ an = เปนลําดับลูเขา
3n + 1
3n 2 − 5n
(11) an = เปนลําดับลูออก
7n − 1
7n 2 7n 2 7
(12) จาก = = 3
5n 2 − 3 ⎛ 3 ⎞
5−
n2 ⎜ 5 − 2 ⎟
⎝ n ⎠ n2
⎛ 3 ⎞
และเนื่องจาก lim 7 = 7 และ lim ⎜ 5 − 2 ⎟ = 5
n →∞
⎝
n →∞ n ⎠
7n 2 lim 7
จะได lim
n →∞ 5n 2 − 3
= n →∞
⎛ 3 ⎞
lim ⎜ 5 − 2 ⎟
n →∞
⎝ n ⎠

33. 33
7
=
5
7n 2
ดังนั้น ลําดับ an = เปนลําดับลูเขา
5n 2 − 3
4n 2 − 2n + 3 2 3
(13) จาก = 4− +
n2 n n2
2 3
และเนื่องจาก lim 4 = 4, lim = 0 และ lim= 0
n →∞ n →∞ n n2
n →∞
⎛ 4n 2 − 2n + 3 ⎞ ⎛ 2 3 ⎞
จะได lim ⎜ ⎟ = lim ⎜ 4 − + 2 ⎟
n →∞
⎝ n2 ⎠ n →∞
⎝ n n ⎠
2 3
= lim 4 − lim + lim 2
n →∞ n →∞ n n →∞ n
= 4–0+0
= 4
4n 2 − 2n + 3
ดังนั้น ลําดับ an = เปนลําดับลูเขา
n2
⎛ 1 ⎞ 1
n2 ⎜ 3 − 2 ⎟ 3− 2
3n − 1
2
⎝ n ⎠
(14) จาก = = 10 n
10n − 5n 2 2 ⎛ 10 ⎞ −5
n ⎜ − 5⎟
⎝n ⎠ n
และเนื่องจาก nlim ⎛ 3 − 12 ⎞ = 3 และ nlim ⎛ 10 − 5 ⎞
⎜ ⎟ →∞ ⎜ n ⎟ = –5
→∞
⎝ n ⎠ ⎝ ⎠
⎛ 1 ⎞
lim ⎜ 3 − 2 ⎟
⎛ 3n 2 − 1 ⎞ n →∞
⎝ n ⎠
จะได nlim ⎜
→∞ 10n − 5n 2
⎟ =
⎝ ⎠ ⎛ 10 ⎞
lim ⎜ − 5 ⎟
n →∞
⎝ n ⎠
3
= −
5
ดังนั้น ลําดับ an = 3n − 1 2 เปนลําดับลูเขา
2
10n − 5n
1
(15) เนื่องจาก lim = 0 และ nlim 1 = 0
→∞ n + 1
n →∞ n
⎛1 1 ⎞ 1 1
จะได lim ⎜ − ⎟ = lim − lim
n →∞ n + 1
n →∞ n
⎝ n +1⎠ n →∞ n
= 0–0
= 0
1 1
ดังนั้น ลําดับ an = − เปนลําดับลูเขา
n n +1

34. 34
n +1
3n +1 3n +1 1⎛ 3⎞
(16) จาก = = ⎜ ⎟
5n + 2 5 ⋅ 5n +1 5⎝ 5⎠
n +1
3n +1 1⎛ 3⎞
จะได lim
n →∞ 5n + 2
= lim ⎜ ⎟
n →∞ 5 5
⎝ ⎠
n +1
1 ⎛3⎞
= lim ⎜ ⎟
5 n →∞ 5
⎝ ⎠
1
= (0)
5
= 0
n +1
3
ดังนั้น ลําดับ an = เปนลําดับลูเขา
5n + 2
n −1
2n −1 + 3 2n −1 3 1 ⎛2⎞ 1
(17) จาก = + n+2 = ⎜ ⎟ +
n +1
3n + 2 27 ⋅ 3n −1
3 27 ⎝ 3 ⎠ 3
⎛ 1 2 n −1 ⎞ 1 ⎛ 1 ⎞
และเนื่องจาก lim ⎜ ⎛ ⎞⎜ ⎟ ⎟ = และ lim ⎜ ⎟ = 0
n →∞ ⎜ 27 ⎝ 3 ⎠
⎝
⎟
⎠ 27 n →∞ ⎜ 3n +1 ⎟
⎝ ⎠
2n −1 + 3 ⎛ 1 2 n −1 1 ⎞
จะได lim
n →∞ 3n + 2
= lim ⎜ ⎛ ⎞
⎜ 27 ⎜ 3 ⎟
+ ⎟
n +1 ⎟
n →∞ ⎝ ⎝ ⎠ 3 ⎠
n −1
1 ⎛2⎞ 1
= lim ⎜ ⎟ + lim n +1
27 n →∞ 3
⎝ ⎠ n →∞ 3
1
= (0) + 0
27
= 0
n −1
2 +3
ดังนั้น ลําดับ an = เปนลําดับลูเขา
3n + 2
⎛ 1 ⎞ 1
n ⎜1 − ⎟ 1−
n −1 ⎝ n⎠ n
(18) จาก = = 1
n +1 ⎛ 1 ⎞ 1+
n ⎜1 + ⎟
⎝ n⎠ n
1 1
และเนื่องจาก lim(1 − ) = 1 และ lim(1 + ) = 1
n →∞ n n →∞ n
⎛ 1 ⎞
lim ⎜ 1 − ⎟
n −1 n →∞
⎝ n⎠
จะได lim =
n →∞ n +1 ⎛ 1 ⎞
lim 1 +
n →∞ ⎜ ⎟
⎝ n⎠
= 1
n −1
ดังนั้น ลําดับ an = เปนลําดับลูเขา
n +1

35. 35
1 1
n 1− 1−
n2 −1 n2 n2
(19) จาก = =
4n 4n 4
1
และเนื่องจาก lim 1 − = 1 และ lim 4 = 4
n →∞ n2 n →∞
1
1−
n2 −1 n2
จะได lim = lim
n →∞ 4n n →∞ 4
1 ⎛ 1 ⎞
= lim ⎜1 − 2 ⎟
4 n →∞ ⎝ n ⎠
1
= 1
4
1
=
4
n2 −1
ดังนั้น ลําดับ an = เปนลําดับลูเขา
4n
1 1
n 4− 4−
4n − 1
2
n2 n2
(20) จาก = =
2n + 3 n 3 + 2 ⎛ 2 ⎞ 2
n⎜ 2 + 3 1+ 3 ⎟ 2 + 3 1+ 3
⎝ n ⎠ n
⎛ 1 ⎞ ⎛ ⎞
และเนื่องจาก lim ⎜ 4 − 2 ⎟
⎜ = 2 และ nlim ⎜ 2 + 3 1 + 23 ⎟ = 3
n →∞
⎝ n ⎟⎠
→∞ ⎜
⎝ n ⎟ ⎠
1
4−
4n − 1
2
n2
จะได lim = lim
n →∞
2n + 3 n 3 + 2 n →∞ 2
2 + 3 1+
n3
⎛ 1 ⎞
lim ⎜ 4 − 2 ⎟
n →∞
⎝ n ⎠
=
⎛ 2 ⎞
lim ⎜ 2 + 3 1 + 3 ⎟
n →∞
⎝ n ⎠
2
=
3
4n − 1
2
ดังนั้น ลําดับ an = เปนลําดับลูเขา
2n + 3 n 3 + 2
( −1)n
(21) an = เปนลําดับลูเขา
n
8n 2 + 5n + 2
(22) an = เปนลําดับลูออก
3 + 2n

36. 36
4. (1) ไมจริง เชน ลําดับ an = n และ ลําดับ bn = –n เปนลําดับลูออก
แตลาดับ (an + bn) = n – n = 0 เปนลําดับลูเขา
ํ
(2) จริง การพิสูจนโดยขอขัดแยง (proof by contradiction) ทําไดดังนี้
สิ่งที่กําหนดใหคือ ลําดับ an เปนลําดับลูเขา และ ลําดับ bn เปนลําดับลูออก
สมมติวา “(an + bn) เปนลําดับลูเขา”
เนื่องจากลําดับ an และลําดับ (an + bn) เปนลําดับลูเขา จึงไดวา lim a และ
 n →∞
n
lim(a n + b n )
n →∞
หาคาได ให lim a n
n →∞
= A และ lim(a n + b n )
n →∞
=B
พิจารณา lim(a n + b n − a n )
n →∞
= lim b n
n →∞
และ lim(a n + b n − a n )
n →∞
= lim(a n + b n ) – lim a n
n →∞ n →∞
= B–A
ดังนั้น lim b n
n →∞
หาคาได ซึ่งทําให ลําดับ bn เปนลําดับลูเขา
เกิดขอขัดแยงกับสิ่งทีกําหนดให
่
จึงสรุปวา ขอความที่สมมติวา “(an + bn) เปนลําดับลูเขา” เปนเท็จ
นั่นคือ (an + bn) ตองเปนลําดับลูออก
r n r n
5. (1) lim P(1 + ) = P lim(1 + )
n →∞ 12 n →∞ 12
n
r ⎛ r ⎞
เนื่องจาก 1+ > 1 ดังนั้น lim ⎜1 + ⎟ หาคาไมได
12 n →∞
⎝ 12 ⎠
n
⎛ r ⎞
ดังนั้น an = P ⎜1 + ⎟ ไมเปนลําดับลูเขา
⎝ 12 ⎠
n
⎛ r ⎞
(2) จาก an = P ⎜1 + ⎟
⎝ 12 ⎠
1.5
กําหนด r = = 0.015
100
⎛ 0.015 ⎞
สิ้นเดือนที่ 1 จะได a1 = 9000 ⎜1 + ⎟ = 9011.25
⎝ 12 ⎠
2
⎛ 0.015 ⎞
สิ้นเดือนที่ 2 จะได a2 = 9000 ⎜1 + ⎟ = 9022.51
⎝ 12 ⎠
3
⎛ 0.015 ⎞
สิ้นเดือนที่ 3 จะได a3 = 9000 ⎜1 + ⎟ = 9033.79
⎝ 12 ⎠
4
⎛ 0.015 ⎞
สิ้นเดือนที่ 4 จะได a4 = 9000 ⎜1 + ⎟ = 9045.08
⎝ 12 ⎠
5
⎛ 0.015 ⎞
สิ้นเดือนที่ 5 จะได a5 = 9000 ⎜1 + ⎟ = 9056.39
⎝ 12 ⎠
6
⎛ 0.015 ⎞
สิ้นเดือนที่ 6 จะได a6 = 9000 ⎜1 + ⎟ = 9067.71
⎝ 12 ⎠

37. 37
7
⎛ 0.015 ⎞
สิ้นเดือนที่ 7 จะได a7 = 9000 ⎜1 + ⎟ = 9079.05
⎝ 12 ⎠
8
⎛ 0.015 ⎞
สิ้นเดือนที่ 8 จะได a8 = 9000 ⎜1 + ⎟ = 9090.39
⎝ 12 ⎠
9
⎛ 0.015 ⎞
สิ้นเดือนที่ 9 จะได a9 = 9000 ⎜1 + ⎟ = 9101.76
⎝ 12 ⎠
10
⎛ 0.015 ⎞
สิ้นเดือนที่ 10 จะได a10 = 9000 ⎜ 1 + ⎟ = 9113.13
⎝ 12 ⎠
ดังนั้น สิบพจนแรกของลําดับ คือ 9011.25, 9022.51, 9033.79, 9045.08, 9056.39,
9067.71, 9079.05, 9090.39, 9101.76, 9113.13
6. (1) ให an เปนงบรายจายปกติทถูกตัดลงเมื่อเวลาผานไป n ป
ี่
A แทนงบรายจายปกติเปน 2.5 พันลานบาท
20 4
สิ้นปที่ 1 จะได a1 = A− (A) = A
100 5
2
4 20 ⎛ 4 ⎞ ⎛4⎞
สิ้นปที่ 2 จะได a2 = A− ⎜ A⎟ = ⎜ ⎟ A
5 100 ⎝ 5 ⎠ ⎝5⎠
2 2 3
⎛4⎞ 20 ⎛ 4 ⎞ ⎛4⎞
สิ้นปที่ 3 จะได a3 = ⎜ ⎟ A− ⎜ ⎟ A = ⎜ ⎟ A
⎝5⎠ 100 ⎝ 5 ⎠ ⎝5⎠
n
⎛4⎞
สิ้นปท่ี n จะได an = ⎜ ⎟ A
⎝5⎠
n
⎛4⎞
ดังนั้น เมื่อเวลาผานไป n ป งบรายจายเปน 2.5 ⎜ ⎟ พันลานบาท
⎝5⎠
4
(2) งบรายจายเมื่อสิ้นปที่ 1 เปน (2.5) = 2 พันลานบาท
5
2
⎛4⎞
งบรายจายเมื่อสิ้นปที่ 2 เปน ⎜ ⎟ (2.5) = 1.6 พันลานบาท
⎝5⎠
3
⎛4⎞
งบรายจายเมื่อสิ้นปที่ 3 เปน ⎜ ⎟ (2.5) = 1.28 พันลานบาท
⎝5⎠
4
⎛4⎞
งบรายจายเมื่อสิ้นปที่ 4 เปน ⎜ ⎟ (2.5) = 1.024 พันลานบาท
⎝5⎠
ดังนั้น งบรายจายในสี่ปแรก หลังถูกตัดงบเปน 2, 1.6, 1.28 และ 1.024 พันลานบาท
ตามลําดับ
n
4 ⎛4⎞
(3) เนื่องจาก < 1 จะได lim 2.5 ⎜ ⎟
n →∞
= 0
5 ⎝5⎠
ดังนั้น ลําดับของงบรายจายนี้เปนลําดับลูเขา

38. 38
เฉลยแบบฝกหัด 1.2 ก
1. (1) ผลบวกยอยของอนุกรมนี้มดังนี้
ี
1
S1 =
2
1 1 2
S2 = + =
2 6 3
1 1 1 13
S3 = + + =
2 6 18 18
n −1
1 1 1 1⎛1⎞ 3n − 1
Sn = + + + ... + ⎜ ⎟ =
2 6 18 2⎝ 3⎠ 4 ⋅ 3n −1
3n − 1
ลําดับผลบวกยอยของอนุกรมนี้คือ 1 , 2 , 13 , ..., , ...
2 3 18 4 ⋅ 3n −1
(2) ผลบวกยอยของอนุกรมนี้มดังนี้
ี
S1 = 3
S2 = 3+2 = 5
S3 = 3+2+4 = 19
3 3
n −1
⎛ ⎛2⎞ n
⎞
Sn = 3 + 2 + 4 + ... + 3 ⎛ 2 ⎞
⎜ ⎟ = 9 ⎜1 − ⎜ ⎟
⎜ ⎝3⎠ ⎟
⎟
3 ⎝3⎠ ⎝ ⎠
19 ⎛ ⎛ 2 ⎞n ⎞
ลําดับผลบวกยอยของอนุกรมนี้คือ 3, 5, , ..., 9 ⎜ 1 − ⎜ ⎟ ⎟ , ...
⎜ ⎝3⎠ ⎟
3 ⎝ ⎠
(3) ผลบวกยอยของอนุกรมนี้มดังนี้
ี
1
S1 =
2
1 5
S2 = + = 3
2 2
1 5 25 31
S3 = + + =
2 2 2 2
1 5 25 1 1
Sn = + + + ... + (5) n −1 = − (1 − 5n )
2 2 2 2 8
ลําดับผลบวกยอยของอนุกรมนี้คือ 1 , 3, 31 , ..., − 1 (1 − 5n ) , ....
2 2 8

39. 39
(4) ผลบวกยอยของอนุกรมนี้มดังนี้
ี
1
S1 =
2
1 1 1
S2 = + (− ) =
2 4 4
1 ⎛ 1⎞ 1 3
S3 = +⎜− ⎟ + =
2 ⎝ 4⎠ 8 8
1⎛ ⎛ 1 ⎞ ⎞
n
1 ⎛ 1⎞ 1 (−1) n −1
Sn = + ⎜ − ⎟ + + ... + = ⎜1 − ⎜ − ⎟ ⎟
2 ⎝ 4⎠ 8 2n 3⎜ ⎝ 2 ⎠
⎝
⎟
⎠
1⎛ ⎛ 1 ⎞ ⎞
n
1 1 3
ลําดับผลบวกยอยของอนุกรมนี้คือ , , , ..., ⎜1 − ⎜ − ⎟ ⎟ , ...
2 4 8 3⎜ ⎝ 2 ⎠ ⎟
⎝ ⎠
(5) ผลบวกยอยของอนุกรมนี้มดังนี้
ี
S1 = 2
S2 = 2 + (–1) = 1
S3 = 2 + (–1) + (–4) = –3
n
Sn = 2 + (–1) + (–4) + ... + (5 – 3n) = (7 − 3n)
2
n
ลําดับผลบวกยอยของอนุกรมนี้คือ 2, 1, –3, ..., (7 − 3n) , ...
2
(6) ผลบวกยอยของอนุกรมนี้มดังนี้
ี
3
S1 =
4
3 9 21
S2 = + =
4 16 16
3 9 27 111
S3 = + + =
4 16 64 64
3 9 27 ⎛3⎞
n
⎛ ⎛ 3 ⎞n ⎞
Sn = + + + ... + ⎜ ⎟ = 3 ⎜1 − ⎜ ⎟ ⎟
⎜ ⎝4⎠ ⎟
4 16 64 ⎝4⎠ ⎝ ⎠
3 21 111 ⎛ ⎛3⎞ ⎞ n
ลําดับผลบวกยอยของอนุกรมนี้คือ , , , ..., 3 ⎜ 1 − ⎜ ⎟ ⎟ , ...
⎜ ⎝4⎠ ⎟
4 16 64 ⎝ ⎠
(7) ผลบวกยอยของอนุกรมนี้มดังนี้
ี
S1 = 0
S2 = 0+3 = 3

40. 40
S3 = 0+3+8 = 11
n
2n 3 + 3n 2 − 5n
Sn = 0 + 3 + + 8 + ... + (n2 – 1) = ∑ (i 2 − 1) =
i =1 6
3
+ 3n 2 − 5n
ลําดับผลบวกยอยของอนุกรมนี้คือ 0, 3, 11, ..., 2n , ...
6
(8) ผลบวกยอยของอนุกรมนี้มดังนี้
ี
S1 = –1
S2 = –1 + 0 = –1
S3 = –1 + 0 + 9 = 8
n 3 3n 4 − 2n 3 − 9n 2 − 4n
Sn = –1 + 0 + 9 + ... + ∑ (i − 2i ) =
2
i=1 12
–1, 8, ..., 3n − 2n − 9n − 4n , ...
4 3 2
ลําดับผลบวกยอยของอนุกรมนี้คือ –1,
12
(9) ผลบวกยอยของอนุกรมนี้มดังนี้
ี
1
S1 = −
10
1 1 9
S2 = − + = −
10 100 100
1 1 1 91
S3 = − + − = −
10 100 1000 1000
1⎛ ⎛ 1⎞ ⎞
n n
1 1 1 ⎛ −1 ⎞
Sn = − + − + ... + ⎜ ⎟ = − ⎜1 − ⎜ − ⎟ ⎟
10 100 1000 ⎝ 10 ⎠ 11 ⎜ ⎝ 10 ⎠
⎝
⎟
⎠
1⎛ ⎛ 1⎞ ⎞
n
1 9 91
ลําดับผลบวกยอยของอนุกรมนี้คือ − , − , − , ..., − ⎜1 − ⎜ − ⎟ ⎟ , ...
10 100 1000 11 ⎜ ⎝ 10 ⎠ ⎟
⎝ ⎠
(10) ผลบวกยอยของอนุกรมนี้มดังนี้
ี
S1 = 100
S2 = 100 + 10 = 110
S3 = 100 + 10 + 1 = 111
1000 ⎛ 1 ⎞
Sn = 100 + 10 + 1 + 0.1 + ... + 103 – n = ⎜1 − n ⎟
9 ⎝ 10 ⎠
1000 ⎛ 1 ⎞
ลําดับผลบวกยอยของอนุกรมนี้คือ 100, 110, 111, ..., ⎜1 − n ⎟ , ...
9 ⎝ 10 ⎠

41. 41
(11) ผลบวกยอยของอนุกรมนี้มีดังนี้
S1 = 1
S2 = 1–2 = –1
S3 = 1–2+3 = 2
S4 = 1–2+3–4 = –2
S5 = 1–2+3–4+5 = 3
S6 = 1–2+3–4+5–6 = –3
ลําดับผลบวกยอยของอนุกรมนี้คือ 1, –1, 2, –2, 3, –3, ...
n −1
1 1 1 1⎛1⎞ 1
2. (1) + + + ... + ⎜ ⎟ + ... เปนอนุกรมเรขาคณิตที่มี r = ซึ่ง | r | < 1
2 6 18 2⎝ 3⎠ 3
1
3
ดังนั้น อนุกรมนี้จึงเปนอนุกรมลูเขาที่มีผลบวกเปน 2
1
=
1− 4
3
(2) อนุกรมลูเขา มีผลบวกเปน 9
1 31
(3) ลําดับผลบวกยอยของอนุกรมนี้คือ , 3, , ..., − 1 (1 − 5n ) , ... ลําดับนี้ไมมีลิมิต
2 2 8
ดังนั้น อนุกรมที่กําหนดให ไมสามารถหาผลบวกได จึงเปนอนุกรมลูออก
1
(4) อนุกรมลูเขา มีผลบวกเปน
3
n
(5) ลําดับผลบวกยอยของอนุกรมนี้คือ 2, 1, –3, ..., (7 − 3n) , ... ลําดับนี้ไมมีลิมิต
2
ดังนั้น อนุกรมที่กําหนดให ไมสามารถหาผลบวกได จึงเปนอนุกรมลูออก
(6) อนุกรมลูเขา มีผลบวกเปน 3
3
+ 3n 2 − 5n
(7) ลําดับผลบวกยอยของอนุกรมนี้คือ 0, 3, 11, ..., 2n , ... ลําดับนี้ไมมีลิมิต
6
ดังนั้น อนุกรมทีกําหนดให ไมสามารถหาผลบวกได จึงเปนอนุกรมลูออก
่
3n 4 − 2n 3 − 9n 2 − 4n
(8) ลําดับผลบวกยอยของอนุกรมนี้คือ –1, –1, 8, ..., , ... ลําดับนี้
12
ไมมีลิมิต ดังนั้น อนุกรมที่กําหนดให ไมสามารถหาผลบวกได จึงเปนอนุกรมลูออก
1
(9) อนุกรมลูเขา มีผลบวกเปน −
11
1000
(10) อนุกรมลูเขา มีผลบวกเปน
9
(11) ลําดับผลบวกยอยของอนุกรมนี้คือ 1, –1, 2, –2, 3, –3, ... ลําดับนี้ไมมีลิมิต
ดังนั้น อนุกรมทีกําหนดให ไมสามารถหาผลบวกได จึงเปนอนุกรมลูออก
่

42. 42
4 + 1 8 + 1 16 + 1 ⎛ 4 8 16 ⎞ ⎛1 1 1 ⎞
3. (1) จะได + + + ... = ⎜ + + + ... ⎟ + ⎜ + + + ... ⎟
9 27 81 ⎝ 9 27 81 ⎠ ⎝ 9 27 81 ⎠
4 1
= 9 + 9
2 1
1− 1−
3 3
⎛ 4⎞ ⎛ 1 ⎞⎛ 3 ⎞
= ⎜ ⎟ (3) + ⎜ ⎟⎜ ⎟
⎝9⎠ ⎝ 9 ⎠⎝ 2 ⎠
4 1
= +
3 6
3
=
2
3 3 3 3 1
(2) อนุกรม 3+ + + + ... + n −1 + ... เปนอนุกรมเรขาคณิตที่มีอัตราสวนรวมเทากับ
2 4 8 2 2
3 3 3 3 3
จะได 3 + + + + ... + n −1 + ... = 1
2 4 8 2 1−
2
3
= 1
2
= 6
1 1 1 1
(3) เมื่อ x เปนจํานวนจริง จะได 2
+
2 2
+
2 3
+ ... +
2 n
+ ...
2+x (2 + x ) (2 + x ) (2 + x )
1
เปนอนุกรมเรขาคณิตที่มีอัตราสวนรวมเทากับ 2
2+x
1
1
เนื่องจาก x2 ≥ 0 ดังนัน 2 + x2
้ ≥ 2 ซึ่งทําให 2
≤ <1
2+x 2
1
1 1 1 1 2
ดังนัน
้ 2
+
2 2
+
2 3
+ ... +
2 n
+ ... = 2+x
1
2+x (2 + x ) (2 + x ) (2 + x ) 1−
2
2+x
1
= 2
x +1
i
4. 0.9 = 0.9999...
= 0.9 + 0.09 + 0.009 + 0.0009 + ...
9 9 9 9
= + 2 + 3 + 4 + ...
10 10 10 10
9 9 9 1
เนื่องจาก + 2 + 3 + ... เปนอนุกรมเรขาคณิต ที่มีอัตราสวนรวมเทากับ
10 10 10 10
9
9 9 9
ดังนั้น + + + ... = 10
1
10 102 103 1−
10
⎛ 9 ⎞⎛ 10 ⎞
= ⎜ ⎟⎜ ⎟
⎝ 10 ⎠⎝ 9 ⎠

43. 43
= 1
i
จะได 0.9 = 1
i i
5. (1) 0.21 = 0.212121...
= 0.21 + 0.0021 + 0.000021 + ...
21 21 21
= + + + ...
102 104 106
21
= 102
1
1− 2
10
⎛ 21 ⎞ ⎛ 10 ⎞
2
= ⎜ 2 ⎟⎜ ⎟
⎝ 10 ⎠ ⎝ 99 ⎠
21 7
= =
99 33
i i
(2) 0.610 4 = 0.6104104...
= 0.6 + 0.0104 + 0.0000104 + 0.0000000104 + ...
6 104 104 104
= + + + + ...
10 104 107 1010
104
6 4
= + 10
10 1 − 1
103
6 104
= +
10 9990
5994 + 104
=
9990
6098
=
9990
i i
(3) 7.256 = 7.25656...
= 7 + 0.2 + 0.056 + 0.00056 + 0.0000056 + ...
2 56 56 56
= 7+ + + + + ...
10 103 105 107
56
2 3
= 7 + + 10
10 1 − 1
102
2 56
= 7+ +
10 990
198 + 56
= 7+
990

44. 44
254
= 7
990
127
= 7
495
i i
(4) 4.387 = 4.38787...
= 4 + 0.3 + 0.087 + 0.00087 + 0.0000087 + ...
3 87 87 87
= 4+ + + + + ...
10 103 105 107
87
3 3
= 4 + + 10
10 1 − 1
102
3 87
= 4+ +
10 990
297 + 87
= 4+
990
384
= 4
990
192
= 4
495
i i
(5) 0.073 = 0.07373...
= 0.073 + 0.00073 + 0.0000073 + ...
73 73 73
= + + + ...
103 105 107
73
= 103
1
1− 2
10
73
=
990
i
(6) 2.9 = 2.999 ...
= 2 + 0.9 + 0.09 + 0.009 + ...
9 9 9
= 2+ + 2 + 3 + ...
10 10 10
9
= 2 + 10
1
1−
10
9
= 2+
9
= 3

45. 45
2
6. เพราะวา 1 + x + x2 + x3 + ... + xn–1 + ... =
3
และเนื่องจาก a1 = 1 , r = x
2 1
จะไดวา =
3 1− x
2 – 2x = 3
1
∴ x = −
2
3 a1 3
7. จาก a1 + a1r + a1r2 + a1r3 + ... = จะได = ---------- (1)
2 1− r 2
3 a1 3
และ a1 – a1r + a1r2 – a1r3 + ... = จะได = ---------- (2)
4 1+ r 4
จาก (1), 2a1 + 3r = 3 ---------- (3)
จาก (2), 4a1 – 3r = 3 ---------- (4)
(3) + (4), 6a1 = 6
∴ a1 = 1
3− 2 1
จาก (3) จะได r = =
3 3
8. (1) รูปสี่เหลี่ยมจัตรัสรูปแรกมีดานยาว 5 หนวย
ุ
2 2
⎛5⎞ ⎛5⎞ 25
ดานของรูปสี่เหลี่ยมจัตุรสรูปที่สองยาว
ั ⎜ ⎟ +⎜ ⎟ =
⎝2⎠ ⎝2⎠ 2
5 2
= หนวย
2
ดังนั้น รูปสี่เหลี่ยมจัตุรัสรูปที่สองมีเสนรอบรูปยาว 10 2 หนวย
2 2
⎛5 2 ⎞ ⎛5 2 ⎞ 5
(2) ดานของรูปสี่เหลี่ยมจัตุรสรูปที่สามยาว
ั ⎜ 4 ⎟ +⎜ 4 ⎟
⎜ ⎟ ⎜ ⎟ = หนวย
⎝ ⎠ ⎝ ⎠ 2
รูปสี่เหลี่ยมจัตรัสรูปที่สามมีเสนรอบรูปยาว 10 หนวย
ุ
2 2
⎛5⎞ ⎛5⎞ 5 2
ดานของรูปสี่เหลี่ยมจัตุรัสรูปที่สี่ยาว ⎜ ⎟ +⎜ ⎟ = หนวย
⎝4⎠ ⎝4⎠ 4
รูปสี่เหลี่ยมจัตรัสรูปที่สี่มีเสนรอบรูปยาว 5 2 หนวย
ุ
จะได ผลบวกของเสนรอบรูปของรูปสี่เหลี่ยมจัตุรัสเปน 20 + 10 2 + 10 + 5 2 + ...
20
=
2
1−
2
= 20(2 + 2)
9. ความยาวของเสนรอบรูปของรูปสามเหลี่ยมรูปแรก เทากับ 30 นิ้ว
ความยาวของเสนรอบรูปของรูปสามเหลี่ยมรูปที่สอง เทากับ 15 นิ้ว
15
ความยาวของเสนรอบรูปของรูปสามเหลี่ยมรูปที่สาม เทากับ นิ้ว
2

46. 46
ผลบวกของความยาวเสนรอบรูปของรูปสามเหลี่ยมทั้งหมดคือ 30 + 15 + 15 + ...
2
30
= 1
1−
2
= 60
∴ ผลบวกความยาวเสนรอบรูปของรูปสามเหลี่ยมทั้งหมดมีคา 60 นิ้ว
10. การแกวงครั้งแรกจากจุดไกลสุดดานหนึ่งไปอีกดานหนึงไดระยะทาง 75 เมตร
่
การแกวงครั้งที่สองไดระยะทาง 75 ⎛ 3 ⎞ เมตร
⎜ ⎟
⎝5⎠
2
⎛3⎞ ⎛3⎞
การแกวงครั้งที่สามไดระยะทาง ⎜ ⎟ 75 ⎜ ⎟ = 75 ⎛ 3 ⎞ เมตร
⎜ ⎟
⎝5⎠ ⎝5⎠ ⎝5⎠
2 3
⎛3⎞ ⎛3⎞
การแกวงครั้งที่สี่ไดระยะทาง ⎜ ⎟ 75 ⎜ ⎟ = 75 ⎛ 3 ⎞ เมตร
⎜ ⎟
⎝5⎠ ⎝5⎠ ⎝5⎠
ระยะทางที่ไดจากการแกวงครั้งใหมเปนเชนนี้ไปเรื่อย ๆ
ดังนั้น เรือไวกิ้งจะแกวงไปมาตั้งแตเริ่มตนจากจุดสูงสุดเปนระยะทางเทากับ
2 3 ⎛ 2 3 ⎞
75 + 75 ⎛ 3 ⎞ + 75 ⎛ 3 ⎞ + 75 ⎛ 3 ⎞ + ... = 75 ⎜1 + 3 + ⎛ 3 ⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎛3⎞
+ ⎜ ⎟ + ... ⎟
⎝5⎠ ⎝5⎠ ⎝5⎠ ⎜ 5 ⎝5⎠ ⎝5⎠ ⎟
⎝ ⎠
⎛ ⎞
⎜ 1 ⎟
= 75 ⎜ 3 ⎟
⎜ 1− ⎟
⎜ ⎟
⎝ 5⎠
= 75 ⎛ 5 ⎞
⎜ ⎟
⎝2⎠
= 187.5 เมตร
11. (1) ให an เปนระยะทางที่สารพิษแพรกระจายตอจากตําแหนงเดิมเมื่อเวลาผานไป n ป
กําหนด a1 = 1500 , a2 = 900 , a3 = 540
สังเกตวา 900 = 540 = 3
1500 900 5
3
สมมติให an เปนลําดับเรขาคณิตที่มีพจนแรกเปน 1500 และมีอัตราสวนรวมเปน
5
ให S10 เปนผลบวกของระยะทางที่สารพิษแพรกระจายไปไดเมื่อสิ้นปที่สิบ
9
จะได S10 = 1500 + 900 + 540 + ... + 1500 ⎛ 3 ⎞
⎜ ⎟
⎝5⎠
⎛ ⎛3⎞ ⎞ 10
1500 ⎜1 − ⎜ ⎟ ⎟
⎜ ⎝5⎠ ⎟
= ⎝ ⎠
3
1−
5

47. 47
5 ⎛ ⎛ 3 ⎞10 ⎞
= (1500 ) ⎜1 − ⎜ ⎟ ⎟
⎜ ⎝5⎠ ⎟
2 ⎝ ⎠
⎛ ⎛ ⎞ ⎞ 10
= 3750 ⎜1 − ⎜ 3 ⎟
⎜ ⎟
⎝ ⎝5⎠ ⎟
⎠
= 3727.325
เมื่อสิ้นปที่สิบ สารพิษจะแพรกระจายไปได 3727.325 เมตร
1500
(2) เพราะวา ผลบวกอนันตของอนุกรมนี้เทากับ 3
= 3750
1−
5
ดังนั้น สารพิษจะแพรกระจายไปไดไกลทีสุด 3,750 เมตร ซึ่งไปไมถึงโรงเรียน
่
2 n −1
2 ⎛2⎞ ⎛2⎞
12. ให Sn แทนผลบวกยอย n พจนแรกของอนุกรม 1 + + ⎜ ⎟ + ... + ⎜ ⎟ + ...
3 ⎝3⎠ ⎝3⎠
⎛ ⎛ 2 ⎞n ⎞
1⎜1 − ⎜ ⎟ ⎟
Sn =
(
a1 1 − r n ) = ⎜ ⎝3⎠ ⎟
⎝ ⎠ =
⎛ ⎛ 2 ⎞n ⎞
3 ⎜1 − ⎜ ⎟ ⎟
1− r 2 ⎜ ⎝3⎠ ⎟
1− ⎝ ⎠
3
5
S1 = 1 S2 = = 1.6666
3
19 65
S3 = = 2.1111 S4 = = 2.4074
9 27
211 665
S5 = = 2.6049 S6 = = 2.7366
81 243
2059 6305
S7 = = 2.8244 S8 = = 2.8829
729 2187
19171 58025
S9 = = 2.9219 S10 = = 2.9479
6561 19683
175099
S11 = = 2.9653
59049
เมื่อ Sn มีคานอยกวา 3 อยูไมเกิน 1 จะได 2 ≤ Sn < 3
เมื่อ Sn มีคานอยกวา 3 อยูไมเกิน 0.2 จะได 2.8 ≤ Sn < 3
เมื่อ Sn มีคานอยกวา 3 อยูไมเกิน 0.05 จะได 2.95 ≤ Sn < 3
จะได n ที่นอยที่สุด ตามเงือนไขขางตนเปน n = 3, n = 7 และ n = 11 ตามลําดับ
 ่
1 1 1
13. ให Sn แทนผลบวกยอย n พจนแรกของอนุกรม 1 + + + ... + + ...
2 3 n
โดยใชเครื่องคํานวณ จะได S1 = 1
3
S2 = = 1.500
2

48. 48
11
S3 = = 1.833
6
25
S4 = = 2.083
12
137
S5 = = 2.283
60
49
S6 = = 2.450
20
363
S7 = = 2.592
140
761
S8 = = 2.717
280
7129
S9 = = 2.828
2520
7381
S10 = = 2.928
2520
83711
S11 = = 3.019
27720
86021
S12 = = 3.103
27720
1145993
S13 = = 3.180
360360
1171733
S14 = = 3.251
360360
1195757
S15 = = 3.318
360360
2436559
S16 = = 3.380
720720
42142223
S17 = = 3.439
12252240
14274301
S18 = = 3.495
4084080
275295799
S19 = = 3.547
77597520

49. 49
55835135
S20 = = 3.597
15519504
18858053
S21 = = 3.645
5173168
19093197
S22 = = 3.690
5173168
444316699
S23 = = 3.734
118982864
1347822955
S24 = = 3.775
356948592
34052522467
S25 = = 3.815
8923714800
34395742267
S26 = = 3.854
8923714800
312536252003
S27 = = 3.891
80313433200
315404588903
S28 = = 3.927
80313433200
9227046511387
S29 = = 3.961
2329089562800
9304682830147
S30 = = 3.994
2329089562800
290774257297357
S31 = = 4.027
72201776446800
ดังนั้น n ที่นอยทีสุด เมื่อ Sn มากกวา 2 คือ 4
 ่
n ที่นอยทีสุด เมื่อ Sn มากกวา 3 คือ 11
่
n ที่นอยทีสุด เมื่อ Sn มากกวา 4 คือ 31
่
14. (1) ไมถูกตอง เพราะ 1 + 2 + 4 + 8 + 16 + 32 + ... เปนอนุกรมอนันตที่เปนอนุกรม
เรขาคณิต อนุกรมนี้มอัตราสวนรวมเปน 2 ซึ่ง | 2 | > 1 จึงไมสามารถหาผลบวกได
ี
(2) ไมถูกตอง เพราะ 1 – 2 + 4 – 8 + 16 – 32 + ... เปนอนุกรมอนันตที่เปนอนุกรม
เรขาคณิต อนุกรมนี้มอัตราสวนรวมเปน –2 ซึ่ง | –2 | > 1 จึงไมสามารถหาผลบวกได
ี

50. 50
a1 (1 − r n )
15. Sn =
1− r
⎛ ⎛ 3 ⎞n ⎞
160 ⎜ 1 − ⎜ ⎟ ⎟
⎜ ⎝2⎠ ⎟
2110 = ⎝ ⎠
3
1−
2
n = 5
16. ใหพจนแรกของอนุกรมเรขาคณิตเปน a และมีอัตราสวนรวมเปน r
จะได a + ar = –3
3
และ ar4 + ar5 = −
16
1
แกระบบสมการขางตน จะได r = หรือ – 1
2 2
1
ถา r = แลวจะได a = –2
2
1
ถา r = – แลวจะได a = –6
2
255
ผลบวก 8 พจนแรกของอนุกรมนี้เทากับ − ทั้งสองกรณี
64
18. เดิมมีแบคทีเรีย 1000 ตัว
120
เมื่อเวลาผานไป 1 ชั่วโมง จะมีแบคทีเรีย (1000) = 1200 ตัว
100
2
⎛ 120 ⎞
เมื่อเวลาผานไป 2 ชั่วโมง จะมีแบคทีเรีย ⎜ ⎟ (1000) = 1440 ตัว
⎝ 100 ⎠
3
⎛ 120 ⎞
เมื่อเวลาผานไป 3 ชั่วโมง จะมีแบคทีเรีย ⎜ ⎟ (1000) = 1728 ตัว
⎝ 100 ⎠
t
⎛ 120 ⎞
ดังนั้น เมื่อเวลาผานไป t ชั่วโมง จะมีแบคทีเรีย ⎜ ⎟ (1000)
⎝ 100 ⎠
10
⎛ 120 ⎞
เมื่อ t = 10 จะได a10 = ⎜ ⎟ (1000) ≈ 6191 ตัว
⎝ 100 ⎠

51. 51
เฉลยแบบฝกหัด 1.2 ข
4
1. (1) ∑ 2i = 2+4+6+8
i =1
52
(2) ∑ ( i + 2 ) = (1 + 2) + (2 + 2) + (3 + 2) + ... + (50 + 2) + (51 + 2) + (52 + 2)
i =1
4
(3) ∑ (10 − 2k ) = (10 – 2) + (10 – 4 ) + (10 – 6) +(10 – 8)
k =1
20
(4) ∑ ( i 2
+ 4) = (12 + 4) + (22 + 4) + (32 + 4) + ... + (182 + 4) + (192 + 4) + (202 + 4)
i =1
5
2. (1) ∑ 3j = 3(1) + 3(2) + 3(3) + 3(4) + 3(5)
j=1
= 3 + 6 + 9 + 12 + 15
= 45
50
(2) ∑ 8 = 8 + 8 + 8 + ... + 8
k =1
50 จํานวน
= 8 x 50
= 400
4
(3) ∑ i ( i − 3) =
2
12(1 – 3) + 22(2 – 3) + 32(3 – 3) + 42(4 – 3)
i =1
= –2 – 4 + 0 + 16
= 10
k+4
6
2+ 4 3+ 4 4+ 4 5+ 4 6+ 4
(4) ∑ = + + + +
k =2 k −1 2 −1 3 −1 4 −1 5 −1 6 −1
7 8 9
= 6+ + + +2
2 3 4
197
=
12
5
(5) ∑(k
k =1
2
+ 3) = (12 + 3) + (22 + 3) + (32 + 3) + (42 + 3) + (52 + 3)
= 4 + 7 + 12 + 19 + 28
= 70
10 10
(6) ∑ (i − 2) = ∑ (i − 6i 2 + 12i − 8 )
3 3
i =1 i =1
10 10 10 10
= ∑i 3
− 6∑ i 2 + 12∑ i − ∑ 8
i =1 i =1 i =1 i =1
2
⎛ 10 (10 + 1) ⎞ ⎛ 10 ⎞ ⎛ (10 )(10 + 1) ⎞
= ⎜ ⎟ − 6 ⎜ (10 + 1)( 20 + 1) ⎟ + 12 ⎜ ⎟ − 80
⎝ 2 ⎠ ⎝6 ⎠ ⎝ 2 ⎠
= 3025 – 2310 + 660 – 80
= 1295

52. 52
15 15 15
(7) ∑ ( i + 5) = ∑i + ∑5
i =1 i =1 i =1
15(16)
= + 5(15)
2
= 195
20 20 9
(8) ∑ ( 2i + 1) = ∑ ( 2i + 1) – ∑ ( 2i + 1)
i =10 i =1 i =1
20 20 9 9
= 2∑ i + ∑1 – 2 ∑ i – ∑1
i =1 i =1 i =1 i =1
2(20)(21) 2(9)(10)
= + 20 – –9
2 2
= 420 + 20 – 90 – 9
= 341
15 15
(9) ∑ ( k + 5) (k − 5)
k =1
= ∑(k
k =1
2
− 25 )
15 15
= ∑ k – ∑ 25
2
k =1 k =1
15(16)(31)
= – 15(25)
6
= 1240 – 375
= 865
∞
3. (1) 1⋅3 + 2⋅4 + 3⋅5 + ... + n(n + 2) + ... = ∑ n ( n + 2)
n =1
n
1 1 1 1 1
(2) + + + ... + = ∑i
4 5 6 n i=4
∞
(3) arp + arp + 1 + arp + 2 + ... + arp + q + ... = ∑ ar p+i
i =0
n
(4) 2 + 4 + 6 + ... + 2n = ∑ 2i
i =1
∞
1 1 1 1 1
(5) + + + ... + + ... = ∑3
3 6 12 3 ( 2n −1 ) n =1 ( 2n −1 )
∞
1 1 1 1 1
(6) + + + ... + + ... = ∑
2+ 1 3+ 2 4+ 3 n + n −1 n =2 n + n −1
n n
4. (1) ∑ 6i = 6∑ i
i =1 i =1
⎛ n ( n + 1) ⎞
= 6⎜ ⎟
⎝ 2 ⎠
= 3n(n + 1)

53. 53
k k k
(2) ∑ ( 2i + 1) = 2∑ i + ∑ 1
i =1 i =1 i =1
⎛ k ( k + 1) ⎞
= 2⎜ ⎟+k
⎝ 2 ⎠
= k2 + k + k
= k2 + 2k
m m
(3) ∑3⋅ 4 i
= 3∑ 4i
i =1 i =1
= 3(4 + 42 + 43 + ... + 4m)
⎛ ( 4 ) (1 − 4m ) ⎞
= 3⎜
⎜ 1− 4
⎟
⎟
⎝ ⎠
= 4m + 1 – 4
n n n
(4) ∑ (i
i =1
2
− i) = ∑ i 2 −∑ i
i =1 i =1
n(n + 1)(2n + 1)
= – n(n + 1)
6 2
n(n + 1) ⎛ 2n + 1 ⎞
= ⎜ 3 − 1⎟
2 ⎝ ⎠
n(n + 1) ⎛ 2n + 1 − 3 ⎞
= ⎜ ⎟
2 ⎝ 3 ⎠
n(n + 1)(2n − 2)
=
6
n(n + 1)(n − 1)
=
3
n −n
3
=
3
10
5. (1) 1 ⋅ 2 + 2 ⋅ 3 + 3 ⋅ 4 + 4 ⋅ 5 + ... + n(n + 1) + ... = ∑ n ( n + 1)
n =1
10 10
= ∑n + ∑n 2
n =1 n =1
10(11)(12) 10 (11)
= +
6 2
= 385 + 55
= 440
(2) 1 ⋅ 4 ⋅ 7 + 2 ⋅ 5 ⋅ 8 + 3 ⋅ 6 ⋅ 9 + ... + n(n + 3)(n + 6) + ...
10
= ∑ n ( n + 3)( n + 6 )
n =1
10 10 10
= ∑ n 3 + 9∑ n 2 + 18∑ n
n =1 n =1 n =1

54. 54
⎛ 10 (11) ⎞ 9 (10 )(11)( 21) 18 (10 )(11)
2
= ⎜ ⎟ + +
⎝ 2 ⎠ 6 2
= 3025 + 3465 + 990
= 7480
(3) 2
1(2 + 3) + 4(4 + 3) + 9(6 + 3) + 16(8 + 3) + ... + n (2n + 3) + ...
10
= ∑ n ( 2n + 3)
2
n =1
10 10
= 2∑ n 3 + 3∑ n 2
i =1 n =1
⎛ 10 (11) ⎞ 3 (10 )(11)( 21)
2
= 2⎜ ⎟ +
⎝ 2 ⎠ 6
= 6050 + 1155
= 7205
(4) 12 + 32 + 52 + 7 2 + ... + (2n − 1) 2 + ...
10
= ∑ ( 2n − 1)
2
n =1
10
= ∑ (4n 2
− 4n + 1)
n =1
10 10 10
= 4∑ n 2 − 4 ∑ n + ∑1
n =1 n =1 n =1
⎛ 10(11)(21) ⎞ ⎛ (10 )(11) ⎞
= 4⎜ ⎟ − 4⎜ ⎟ + 10
⎝ 6 ⎠ ⎝ 2 ⎠
= 1540 – 220 + 10
= 1330
⎛ 1⎞ ⎛ 1 ⎞ ⎛ 1 ⎞ ⎛ 1⎞
= ∑ n ⎛1 + 1 ⎞
10
(5) 1⎜ 1 + ⎟ + 2 ⎜ 1 + ⎟ + 3 ⎜ 1 + ⎟ + ... + n ⎜ 1 + ⎟ + ... ⎜ ⎟
⎝ 1⎠ ⎝ 2 ⎠ ⎝ 3 ⎠ ⎝ n⎠ ⎝ n⎠
n =1
10
= ∑ ( n + 1)
n =1
10 10
= ∑ n + ∑1
n =1 n =1
10 (11)
= + 10
2
= 65
6. (1) 1 ⋅ 2 ⋅ 3 + 2 ⋅ 3 ⋅ 4 + 3 ⋅ 4 ⋅ 5 + ... + n(n + 1)(n + 2) + ... + 10 ⋅ 11 ⋅ 12
10
= ∑ n ( n + 1)( n + 2 )
n =1

55. 55
10 10 10
= ∑ n 3 + 3∑ n 2 + 2∑ n
n =1 n =1 n =1
⎛ 10 (11) ⎞ 3 (10 )(11)( 21) 2 (10 )(11)
2
= ⎜ ⎟ + +
⎝ 2 ⎠ 6 2
= 3025 + 1155 + 110
= 4290
(2) 1 ⋅ 2 + 2 ⋅ 3 + 3 ⋅ 4 + ... + n(n + 1) + ... + 99 ⋅ 100
99
= ∑ n ( n + 1)
n =1
99 99
= ∑ n2 + ∑ n
n =1 n =1
99 (100 )(199 ) 99 (100 )
= +
6 2
= 328350 + 4950
= 333300
(3) จํานวนเต็มระหวาง 1 ถึง 100 ทีหารดวย 4 แลวเหลือเศษ 3 คือ 7, 11, 15, ... , 99
่
24
อนุกรม 7 + 11 + 15 + ... + (4n + 3) + ... + 99 เขียนแทนดวย ∑ ( 4n + 3)
n =1
24 24 24
จะได ∑ ( 4n + 3) = 4∑ n + ∑ 3
n =1 n =1 n =1
4 ( 24 )( 25 )
= + ( 24 )( 3)
2
= 1200 + 72
= 1272
ผลบวกของจํานวนเต็มทังหมดระหวาง 1 ถึง 100 ทีหารดวย 4 แลวเหลือเศษ 3 เปน 1272
้ ่
n
1 n
⎛1 1 ⎞
7. (1) ∑ i ( i + 1) = ∑⎜ i − i +1⎟
i =1 ⎝
i =1 ⎠
⎛ 1⎞ ⎛1 1⎞ ⎛1 1⎞ ⎛1 1 ⎞
Sn = ⎜ 1 − ⎟ + ⎜ − ⎟ + ⎜ − ⎟ + ... + ⎜ − ⎟
⎝ 2⎠ ⎝ 2 3⎠ ⎝3 4⎠ ⎝ n n +1⎠
1 n
= 1− =
n +1 n +1
20
S20 =
21
n
1 1 n ⎛ 1 1 ⎞
(2) ∑ ( 2i − 1)( 2i + 1) = ∑ ⎜ 2i − 1 − 2i + 1 ⎟
i =1 2 i =1 ⎝ ⎠
1 ⎡⎛ 1 ⎞ ⎛ 1 1 ⎞ ⎛ 1 1 ⎞ ⎛ 1 1 ⎞⎤
Sn = ⎢⎜1 − 3 ⎟ + ⎜ 3 − 5 ⎟ + ⎜ 5 − 7 ⎟ + ... + ⎜ 2n − 1 − 2n + 1 ⎟ ⎥
2 ⎣⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠⎦

56. 56
1⎛ 1 ⎞ n
= ⎜1 − ⎟ =
2 ⎝ 2n + 1 ⎠ 2n + 1
20
S20 =
41
n
1
(3) ให Sn = ∑ i ( i + 1)( i + 2 )
i =1
1 1⎛ 1 1 ⎞
จะได a1 = = ⎜ − ⎟
1⋅ 2 ⋅ 3 2 ⎝ 1⋅ 2 2 ⋅ 3 ⎠
1 1⎛ 1 1 ⎞
a2 = = ⎜ − ⎟
2⋅3⋅ 4 2 ⎝ 2 ⋅3 3⋅ 4 ⎠
1 1⎛ 1 1 ⎞
a3 = = ⎜ − ⎟
3⋅ 4 ⋅5 2 ⎝ 3⋅ 4 4⋅5 ⎠
1 1⎛ 1 1 ⎞
an = = ⎜ − ⎟
n ( n + 1)( n + 2 ) 2 ⎜ n ( n + 1) ( n + 1)( n + 2 ) ⎟
⎝ ⎠
Sn = a1 + a2 + a3 + ... + an
1 ⎡⎛ 1 1 ⎞ ⎛ 1 1 ⎞ ⎛ 1 1 ⎞⎤
= ⎢⎜ − ⎟ + ⎜ − ⎟ + ... + ⎜
⎜ − ⎟⎥
⎟
2 ⎢⎝ 2 6 ⎠ ⎝ 6 12 ⎠
⎣ ⎝ n ( n + 1) ( n + 1)( n + 2 ) ⎠ ⎥
⎦
1⎛1 1 ⎞
= ⎜ −
⎜ 2 ( n + 1)( n + 2 ) ⎟
⎟
2⎝ ⎠
1⎛1 1 ⎞ 115
S20 = ⎜ − ⎟ =
2 ⎝ 2 21 ⋅ 22 ⎠ 462
n
1 1 n ⎛1 1 ⎞
(4) ∑ i (i + 2) = ∑⎜ i − i + 2 ⎟
i =1 2 i =1 ⎝ ⎠
1 ⎡⎛ 1 ⎞ ⎛ 1 1 ⎞ ⎛ 1 1 ⎞ ⎛1 1 ⎞⎤
Sn = ⎢⎜1 − 3 ⎟ + ⎜ 2 − 4 ⎟ + ⎜ 3 − 5 ⎟ + ... + ⎜ n − n + 2 ⎟ ⎥
2 ⎣⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠⎦
1⎡ 1 1 1 ⎤
= ⎢1 + 2 − n + 1 − n + 2 ⎥
2⎣ ⎦
1⎛3 2n + 3 ⎞
= ⎜ − ⎟
2 ⎜ 2 ( n + 1)( n + 2 ) ⎟
⎝ ⎠
1⎛3 43 ⎞ 325
S20 = ⎜ − ⎟ =
2 ⎝ 2 21 ⋅ 22 ⎠ 462
8. (1) ให Sn แทนผลบวกของอนุกรมนี้
Sn = 1 + 2⋅2 + 3⋅22 + 4⋅23 + ... + n⋅2n–1 ---------- (1)
(1) × 1 , 2Sn = 1⋅2 + 2⋅22 + 3⋅23 + ... + (n – 1)⋅2n–1 + n⋅2n ---------- (2)
5
(1) – (2), –Sn = 1 + (2 – 1)2 + (3 – 2)22 + (4 – 3)23 + … + (n – n + 1)2n-1 – n⋅2n

57. 57
= 1 + 2 + 22 + 23 + ... + 2n–1 – n⋅2n
1(1 − 2n )
–Sn = − n ⋅ 2n
1− 2
–Sn = –1(1 – 2n) – n⋅2n
Sn = (1 – 2n) + n⋅2n
จะได S10 = (1 – 210) + 10⋅210
= –1023 + 10240
= 9217
(2) ให Sn แทนผลบวกของอนุกรมนี้
1 1 1 1
Sn = 1 ⋅ + 2 ⋅ 2 + 3 ⋅ 3 + ... + n ⋅ n ---------- (1)
5 5 5 5
1 1 1 1 1
(1) × (2), Sn = 1 ⋅ 2 + 2 ⋅ 3 + ... + (n − 1) ⋅ n + n ⋅ n +1 ---------- (2)
5 5 5 5 5
4 1 1 1 1 1
(1) – (2), Sn = + (2 − 1) ⋅ 2 + (3 − 2) ⋅ 3 + ... + (n − (n − 1)) ⋅ n − n ⋅ n +1
5 5 5 5 5 5
1 1 1 1 1
= + + + ... + n − n ⋅ n +1
5 52 53 5 5
1⎛ ⎛1⎞ ⎞
n
⎜1 − ⎜ ⎟ ⎟
4 5⎜ ⎝ 5⎠ ⎟
⎝ ⎠ −n⋅ 1
Sn =
5 1−
1 5n +1
5
4 1 1 1
Sn = (1 − n ) − n ⋅ n +1
5 4 5 5
5 1 1
Sn = (1 − n ) − n ⋅
16 5 4 ⋅ 5n
5 1 1
จะได S10 = (1 − 10 ) −
16 5 2 ⋅ 59
2n + 1 1 1
9. (1) = −
n ( n + 1) ( n + 1)
2 2 2
2
n
3 5 7 2n + 1
ให Sn = + + + ... + 2
1 ⋅ 4 4 ⋅ 9 9 ⋅ 16 n ( n + 1)
2
⎛1 1 ⎞ ⎛ 1 1 ⎞ ⎛ 1 1 ⎞
= ⎜ − ⎟ + ⎜ − ⎟ + ... + ⎜ 2 −
⎜n
⎟
( n + 1) ⎟
2
⎝1 4 ⎠ ⎝ 4 9 ⎠ ⎝ ⎠
1
= 1−
( n + 1)
2
n 2 + 2n
=
( n + 1)
2
n 2 + 2n
ผลบวก n พจนแรก เปน
( n + 1)
2

58. 58
2 −1 3− 2 2− 3 n +1 − n
(2) ให Sn = + + + ... +
1⋅ 2 2⋅ 3 3⋅2 n n +1
⎛ 1 ⎞ ⎛ 1 1 ⎞ ⎛ 1 1⎞ ⎛ 1 1 ⎞
= ⎜1 − ⎟+⎜ − ⎟+⎜ − ⎟ + ... + ⎜ − ⎟
⎝ 2⎠ ⎝ 2 3⎠ ⎝ 3 2⎠ ⎝ n n +1 ⎠
1
= 1−
n +1
1
ผลบวก n พจนแรก เปน 1−
n +1
∞ ∞ n −1
−(n −1) ⎛1⎞
10. (1) เนื่องจาก ∑ e = ∑⎜e⎟
n =1 n =1 ⎝ ⎠
1 1 1
Sn =
1+ +
2
+ ... +
n −1
e e e
⎛ 1 ⎞
1⎜1 − n ⎟
= ⎝e ⎠
1
1−
e
1
1− n
e
lim Sn = lim e
1
=
n →∞ n →∞ e −1
1−
e
e
ดังนั้น อนุกรมนี้เปนอนุกรมลูเขา และมีผลบวกเทากับ
e −1
(2) ลําดับผลบวกยอยของอนุกรมนี้คือ 1, –1, 3, –5, 11, ...
อนุกรมนี้เปนอนุกรมลูออก
9 9 9 9
(3) Sn = + + + ... +
100 1002 1003 100n
9 ⎛ 1 ⎞
⎜1 − n⎟
= 100 ⎝ 100 ⎠ = 1 ⎛1 − 1 n ⎞
1 ⎜ ⎟
11 ⎝ 100 ⎠
1−
100
1⎛ 1 ⎞ 1
lim Sn = lim ⎜ 1 − n ⎟ = 11
n →∞ n →∞ 11
⎝ 100 ⎠
1
ดังนั้น อนุกรมนี้เปนอนุกรมลูเขา และมีผลบวกเทากับ
11
5 10 15 20 25 5n
(4) ลําดับผลบวกยอยของอนุกรมนี้คือ , , , , , ..., , ...
2 3 4 5 6 n +1
5n
เนื่องจาก lim = 5
n →∞ n +1
ดังนั้น อนุกรมนี้เปนอนุกรมลูเขา และมีผลบวกเทากับ 5

59. 59
∞ 2n + 1 ∞ ⎛ 1 1 ⎞
(5) ∑ = ∑ ⎜ − ⎟
n =1 n 2 (n + 1) 2 n =1⎜ n 2 (n + 1) 2 ⎟
⎝ ⎠
⎛ 1 ⎞ ⎛ 1 1 ⎞ ⎛ 1 1 ⎞ ⎛ 1 1 ⎞
Sn = ⎜ 1− ⎟ +⎜ − ⎟ + ⎜ 2 − 2 ⎟ + ... + ⎜ 2 −
⎜ ⎟
⎝ 22 ⎠ ⎝ 22 32 ⎠ ⎝ 3 4 ⎠ ⎝n (n + 1) 2 ⎟
⎠
1
= 1−
(n + 1) 2
⎛ 1 ⎞
lim Sn
n →∞
= lim ⎜1 −
n →∞ ⎜ 2⎟
⎟
= 1
⎝ (n + 1) ⎠
ดังนั้น อนุกรมนี้เปนอนุกรมลูเขา และมีผลบวกเทากับ 1
⎛ 1 ⎞ ⎛ 1 1 ⎞ ⎛ 1 1 ⎞ ⎛ 1 1 ⎞
(6) Sn = ⎜1 − ⎟+⎜ − ⎟+⎜ − ⎟ + ... + ⎜ − ⎟
⎝ 2⎠ ⎝ 2 3⎠ ⎝ 3 4⎠ ⎝ n n +1 ⎠
1
= 1−
n +1
⎛ 1 ⎞
lim Sn = lim ⎜1 − ⎟ = 1
n →∞ n →∞
⎝ n +1 ⎠
ดังนั้น อนุกรมนี้เปนอนุกรมลูเขา และมีผลบวกเทากับ 1
16 4
(7) อนุกรมที่กําหนดใหเปนอนุกรมเรขาคณิตที่มี a1 = และ r =
5 5
เนื่องจาก | r | < 1 อนุกรมนี้จึงเปนอนุกรมลูเขา
16
a1
และมีผลบวกเทากับ = 5 = 16
1− r 1−
4
5
∞ 1 1 ∞ 2
(8) ∑
2 −1
= ∑
n =1 4n 2 n =1 (2n + 1)(2n − 1)
∞
= 1 ∑⎛ 1 − 1 ⎞
⎜ ⎟
2 n =1⎝ 2n − 1 2n + 1 ⎠
1 ⎛⎛ 1 ⎞ ⎛ 1 1 ⎞ ⎛ 1 1 ⎞ ⎛ 1 1 ⎞⎞
Sn = ⎜ ⎜1 − 3 ⎟ + ⎜ 3 − 5 ⎟ + ⎜ 5 − 7 ⎟ + ... + ⎜ 2n − 1 − 2n + 1 ⎟ ⎟
2 ⎝⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠⎠
1⎛ 1 ⎞
= ⎜1 − ⎟
2 ⎝ 2n + 1 ⎠
lim Sn = lim 1 ⎛1 − 1 ⎞ = 1
⎜ ⎟
n →∞ n →∞ 2
⎝ 2n + 1 ⎠ 2
1
ดังนั้น อนุกรมนี้เปนอนุกรมลูเขา และมีผลบวกเทากับ
2

60. 60
11. ใหอนุกรมนี้คอ a1 + a2 + a3 + ... + an + ... โดยที่ an = 2n – 5
ื
15 15
จะได ผลบวกของ 15 พจนแรกของอนุกรมนี้ คือ ∑ a n = ∑ (2n − 5)
n =1 n =1
15 15
= 2 ∑ n– ∑ 5
n =1 n =1
⎛ 15(16) ⎞
= 2⎜ ⎟ –15(5)
⎝ 2 ⎠
= 240 – 75
= 165
12. (1) ลําดับของจํานวนเต็มระหวาง 9 กับ 199 ที่ 8 หารลงตัวคือ 16, 24, 32, ..., 192
เพราะวา an = a1 + (n – 1)8
จะได 192 = 16 + (n – 1)8
⎛ 192 − 16 ⎞
n = ⎜ ⎟ +1
⎝ 8 ⎠
n = 23
n
จาก Sn = (a1 + a n )
2
23
จะได S23 = (16 + 192)
2
= 2392
ดังนัน ผลบวกของจํานวนเต็มที่อยูระหวาง 9 กับ 199 ที่ 8 หารลงตัวเทากับ 2392
้
(2) ลําดับของจํานวนเต็มระหวาง 9 กับ 199 คือ 10, 11, 12, ..., 198 ซึ่งมี 189 จํานวน
189
จะได S189 = (10 + 198)
2
= 19656
ผลบวกของจํานวนเต็มทีอยูระหวาง 9 กับ 199 เปน 19656
่
จะไดผลบวกของจํานวนเต็มที่อยูระหวาง 9 กับ 199 ที่ 8 หารไมลงตัวเปน
19656 – 2392 = 17264
13. (1) e
(2) π
(3) ln 2