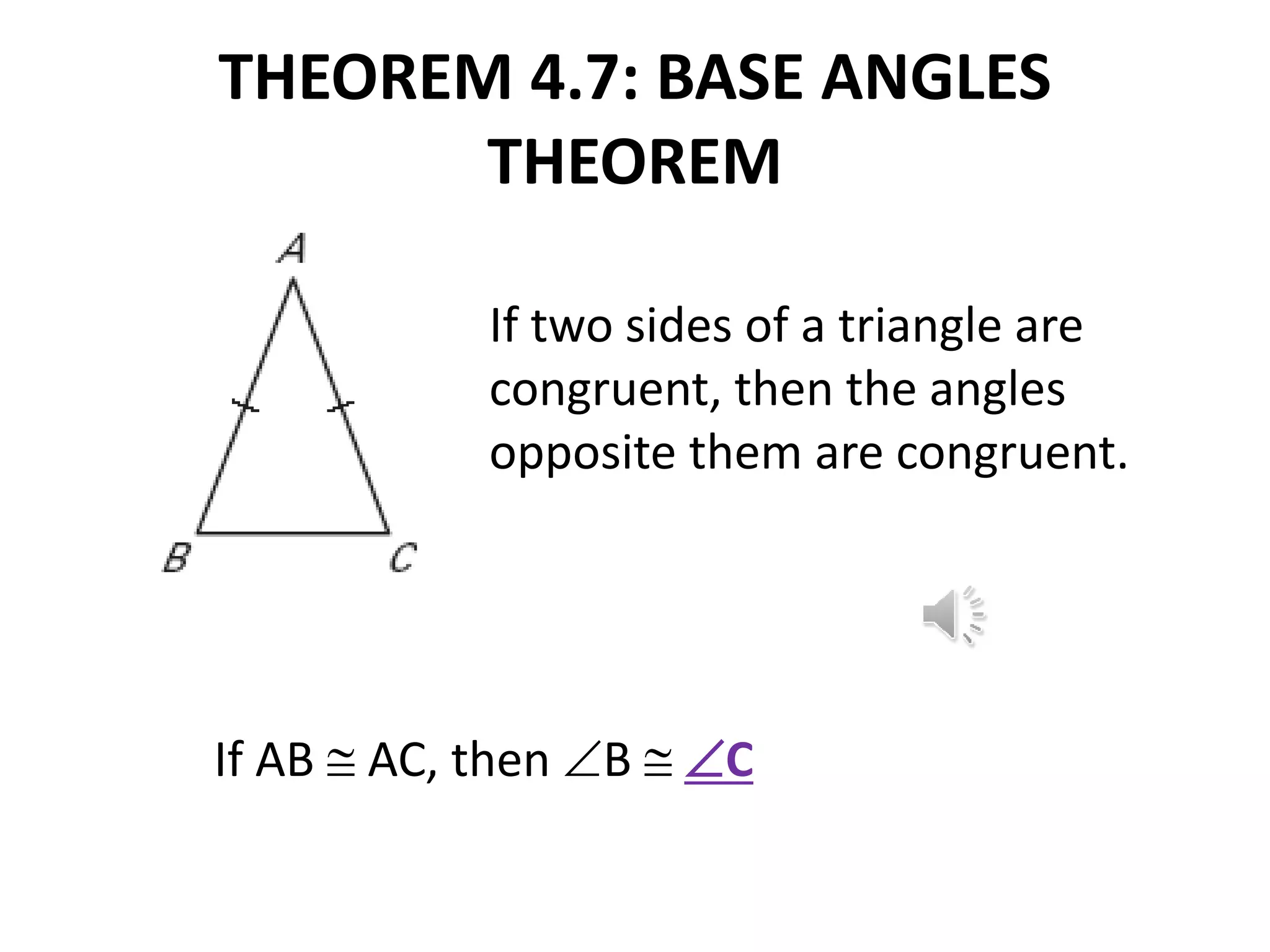
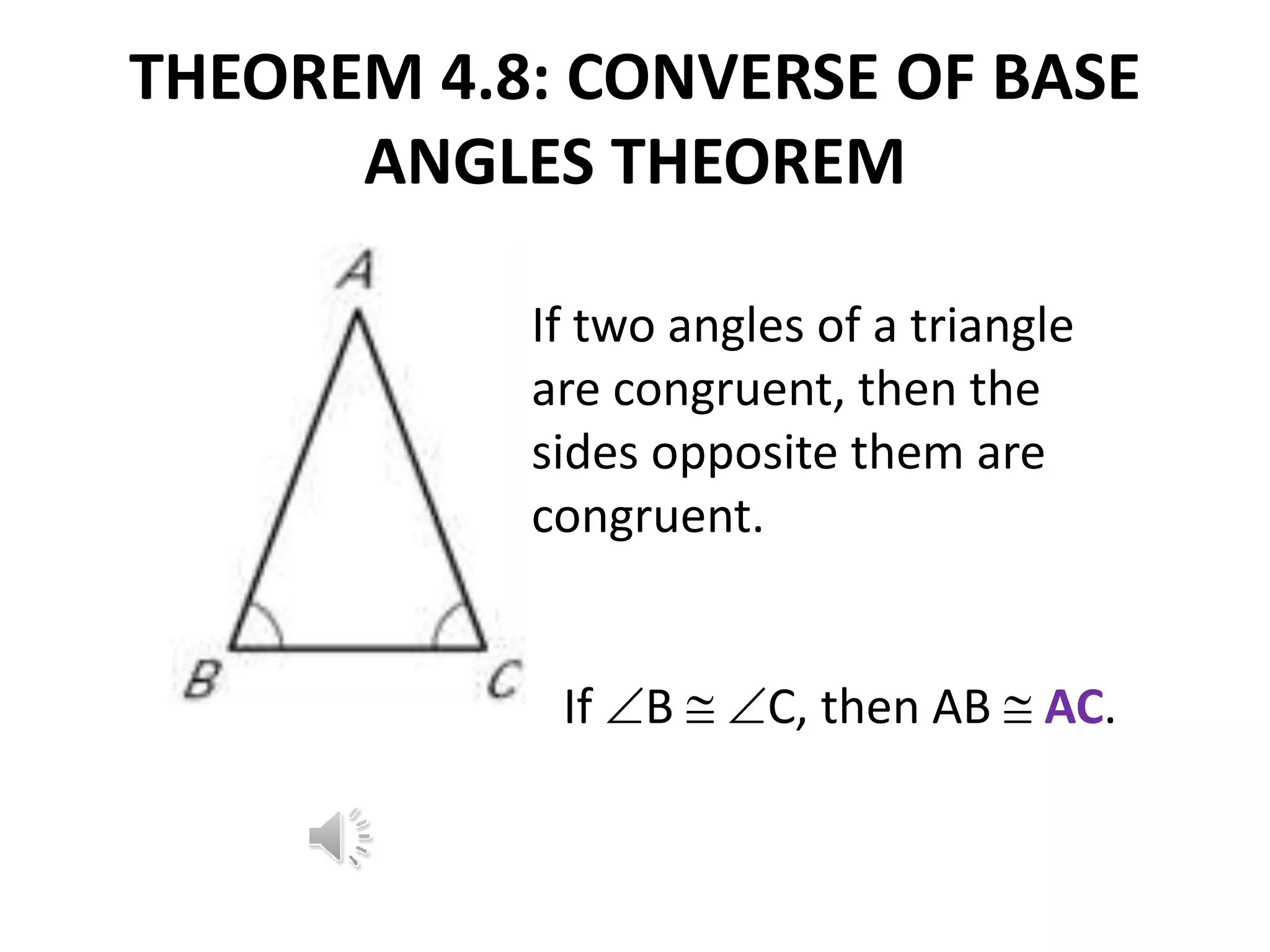
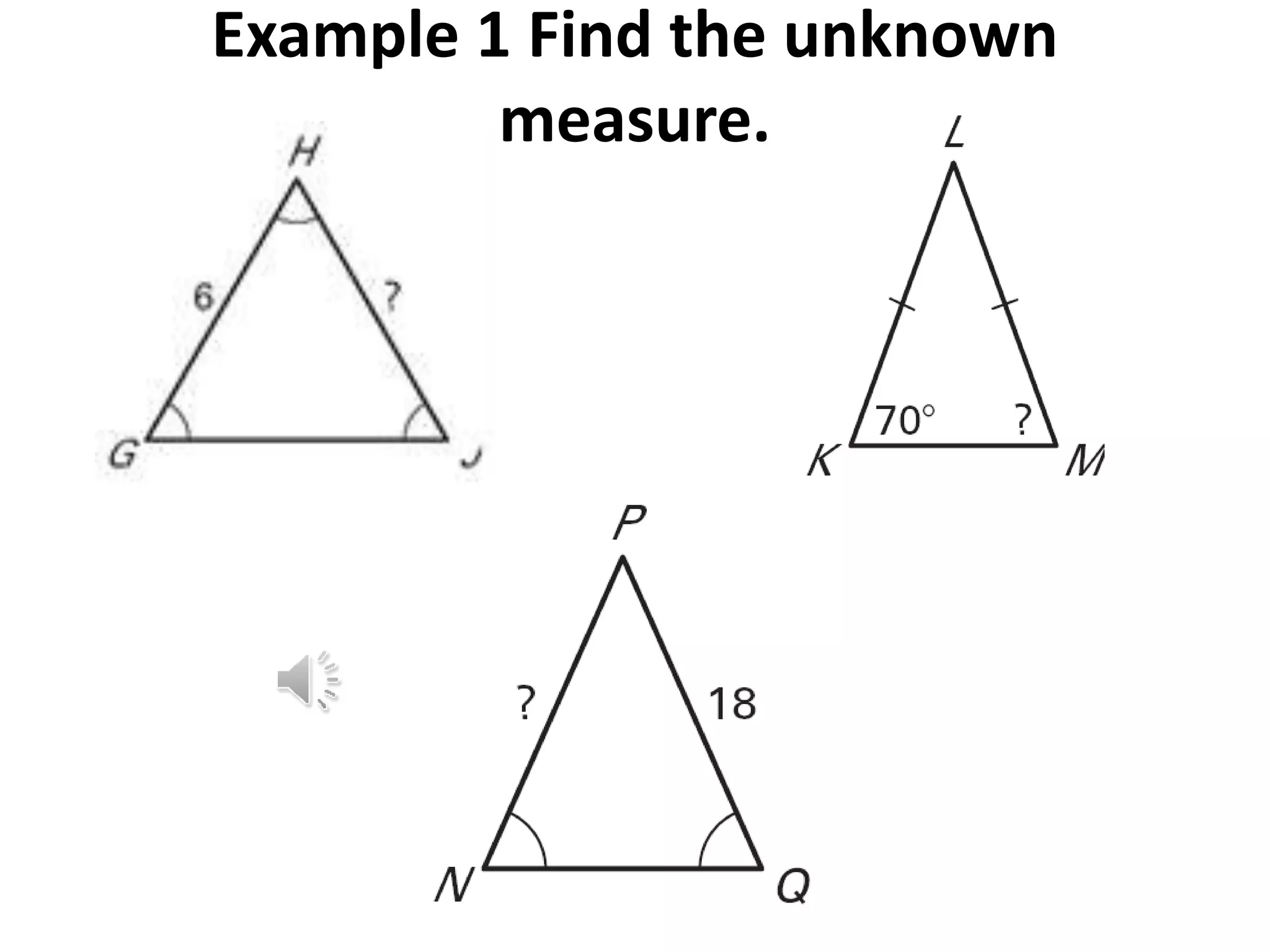
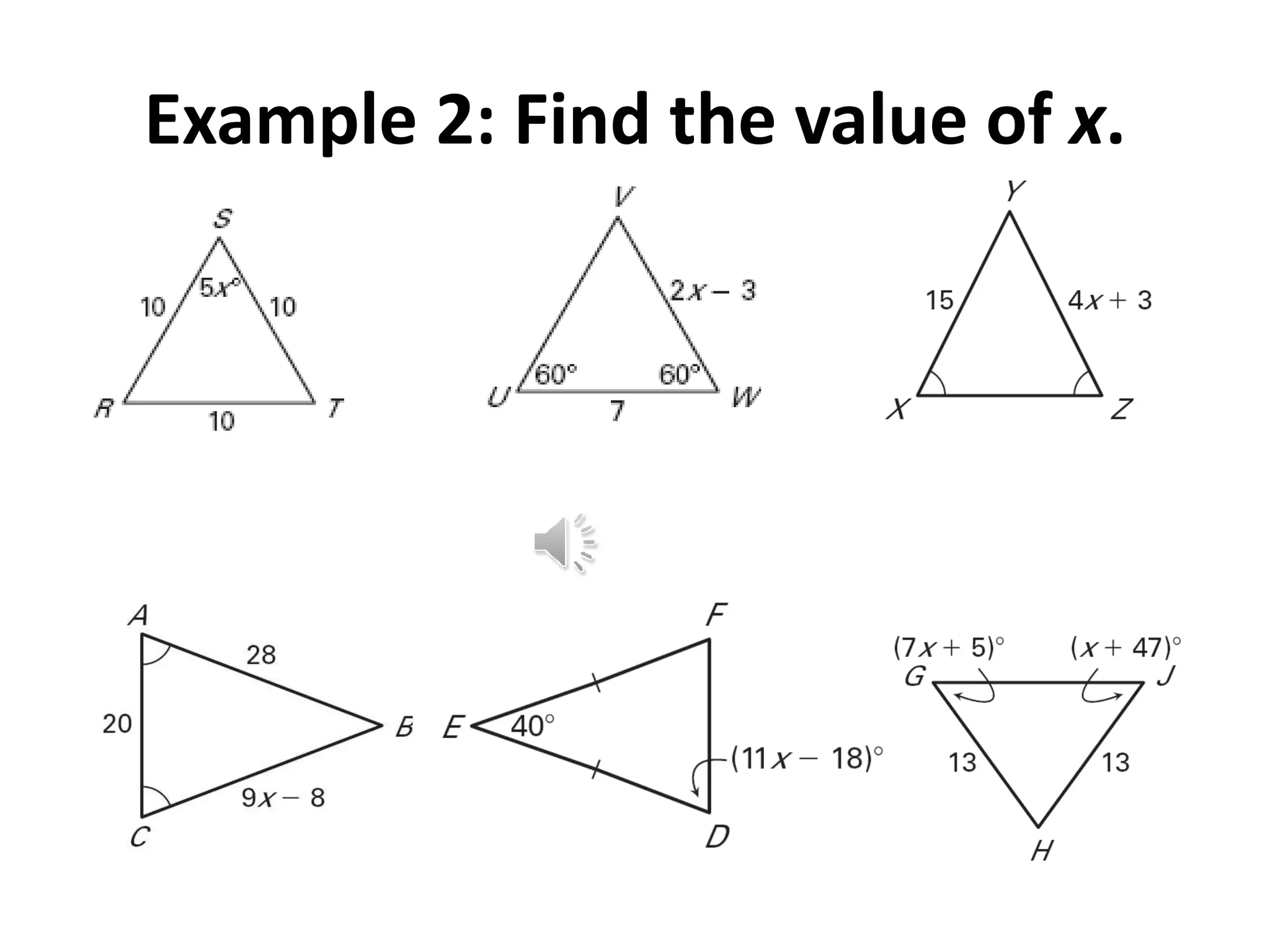
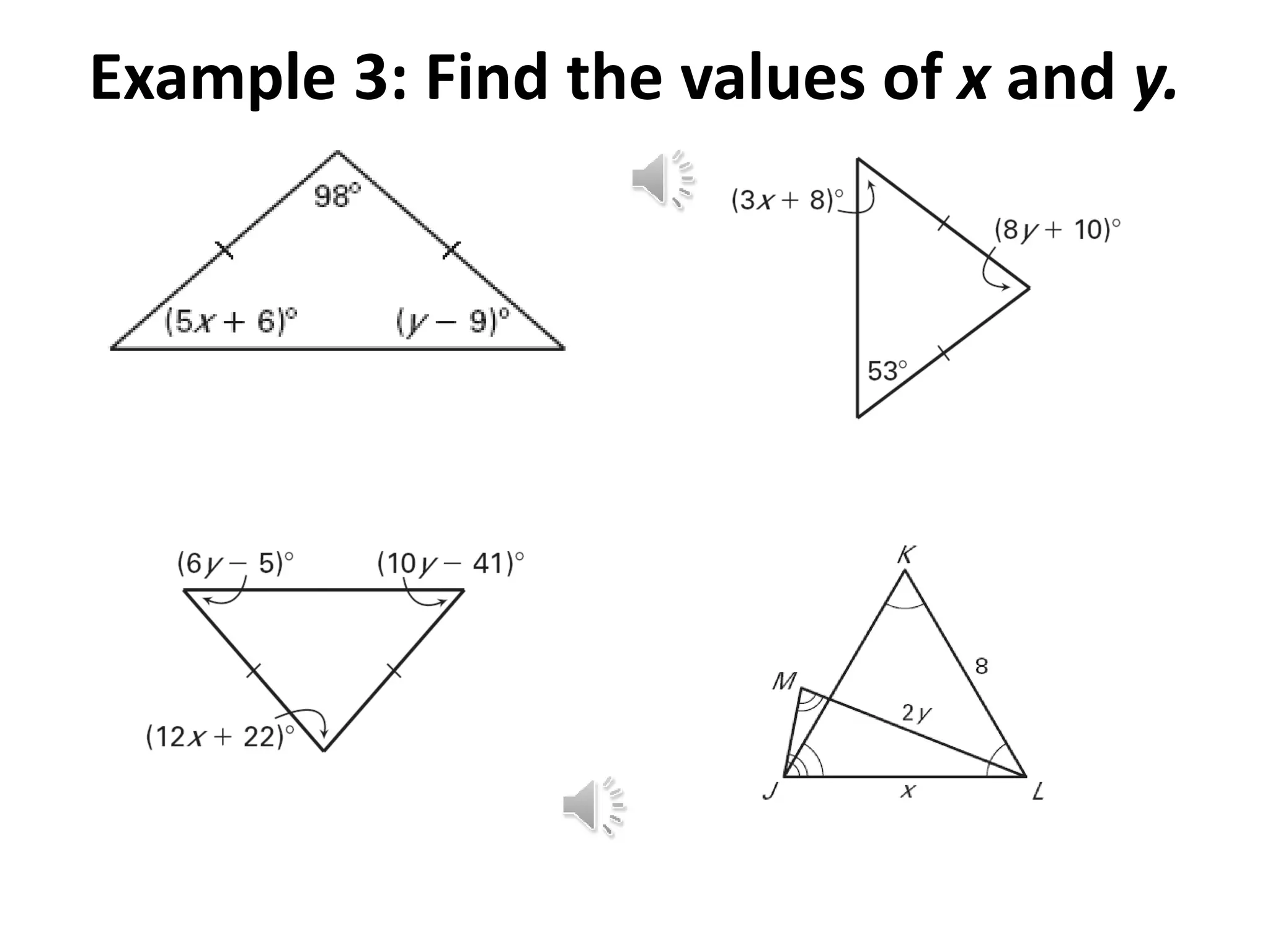
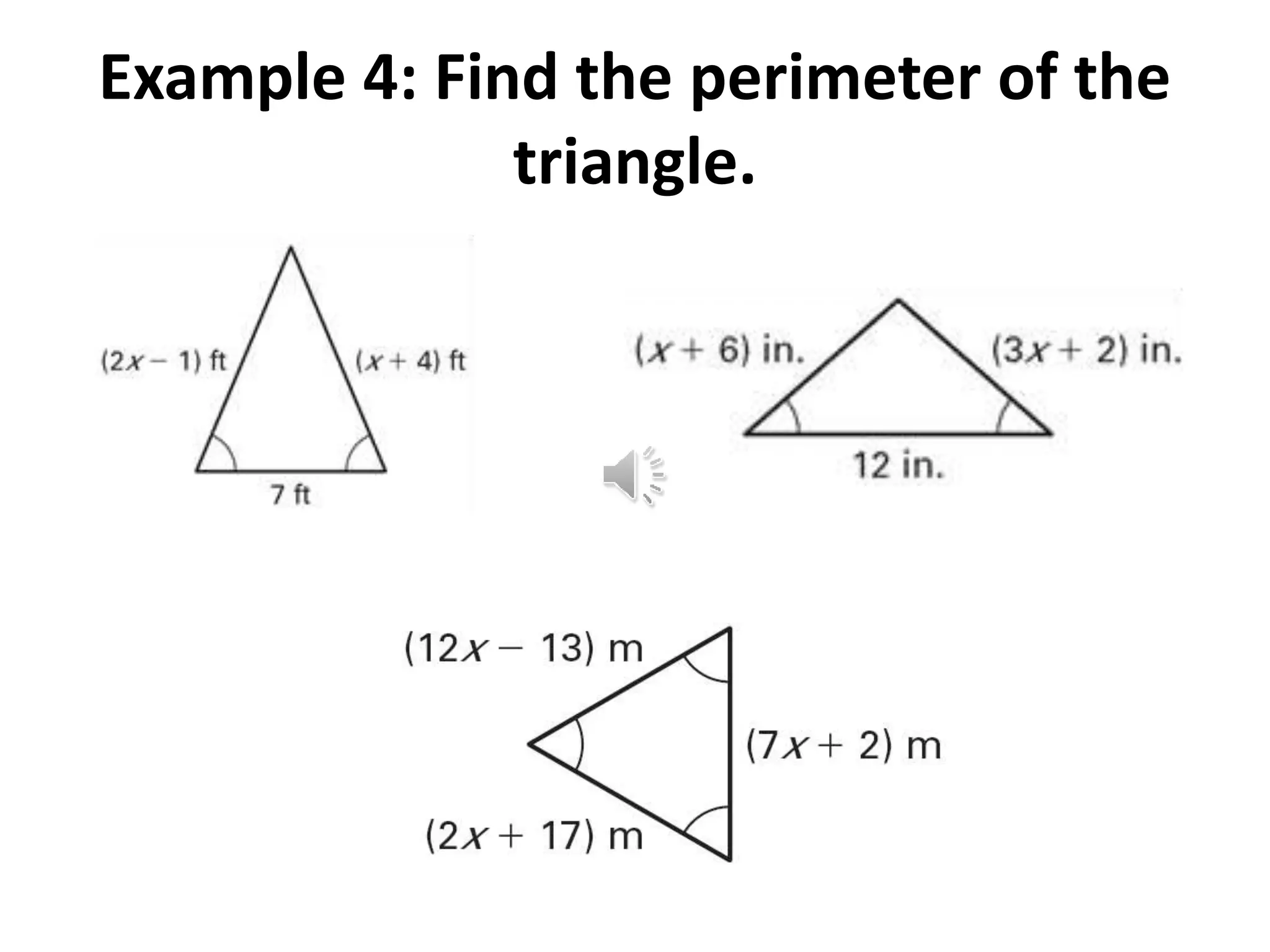
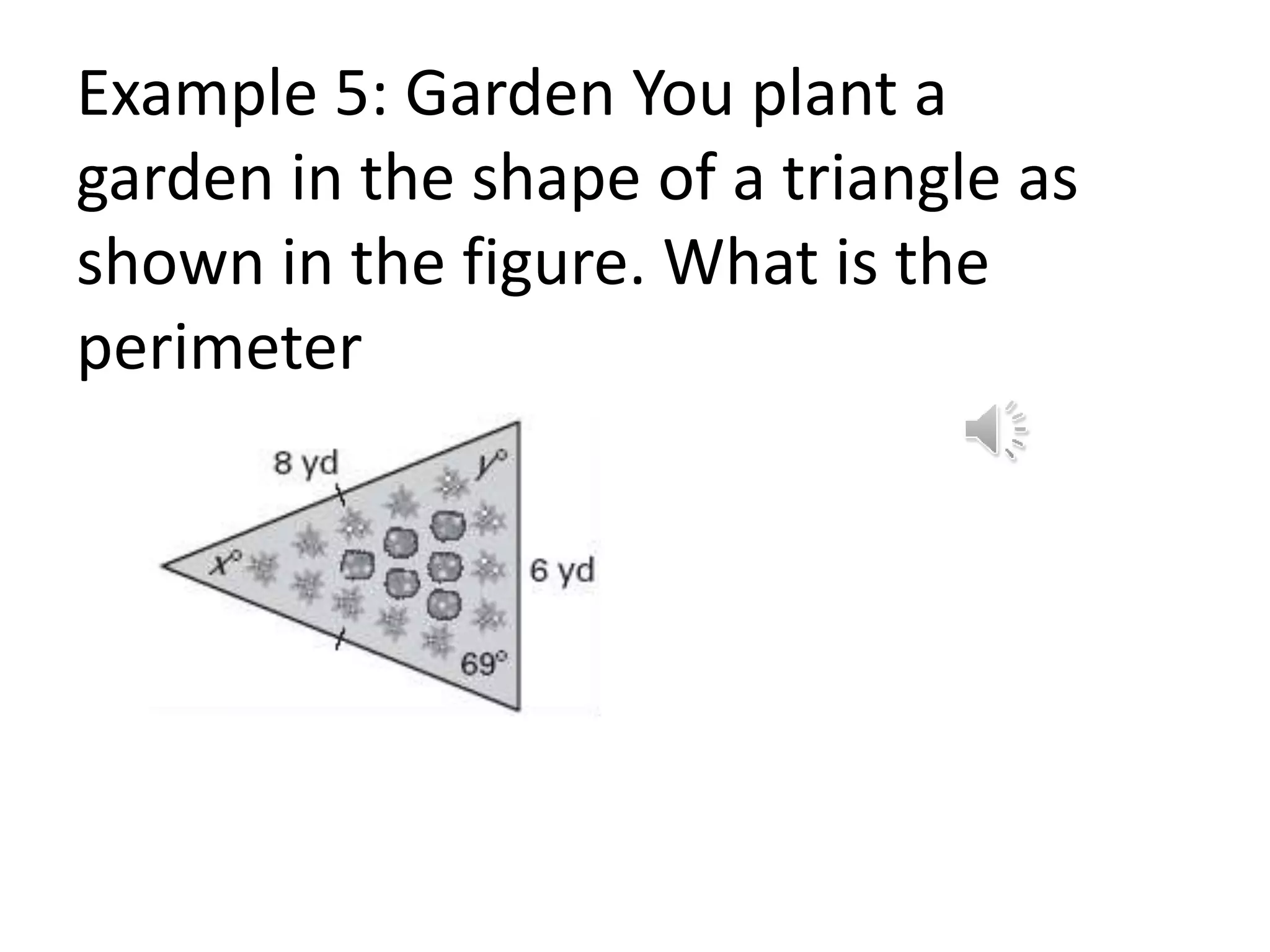
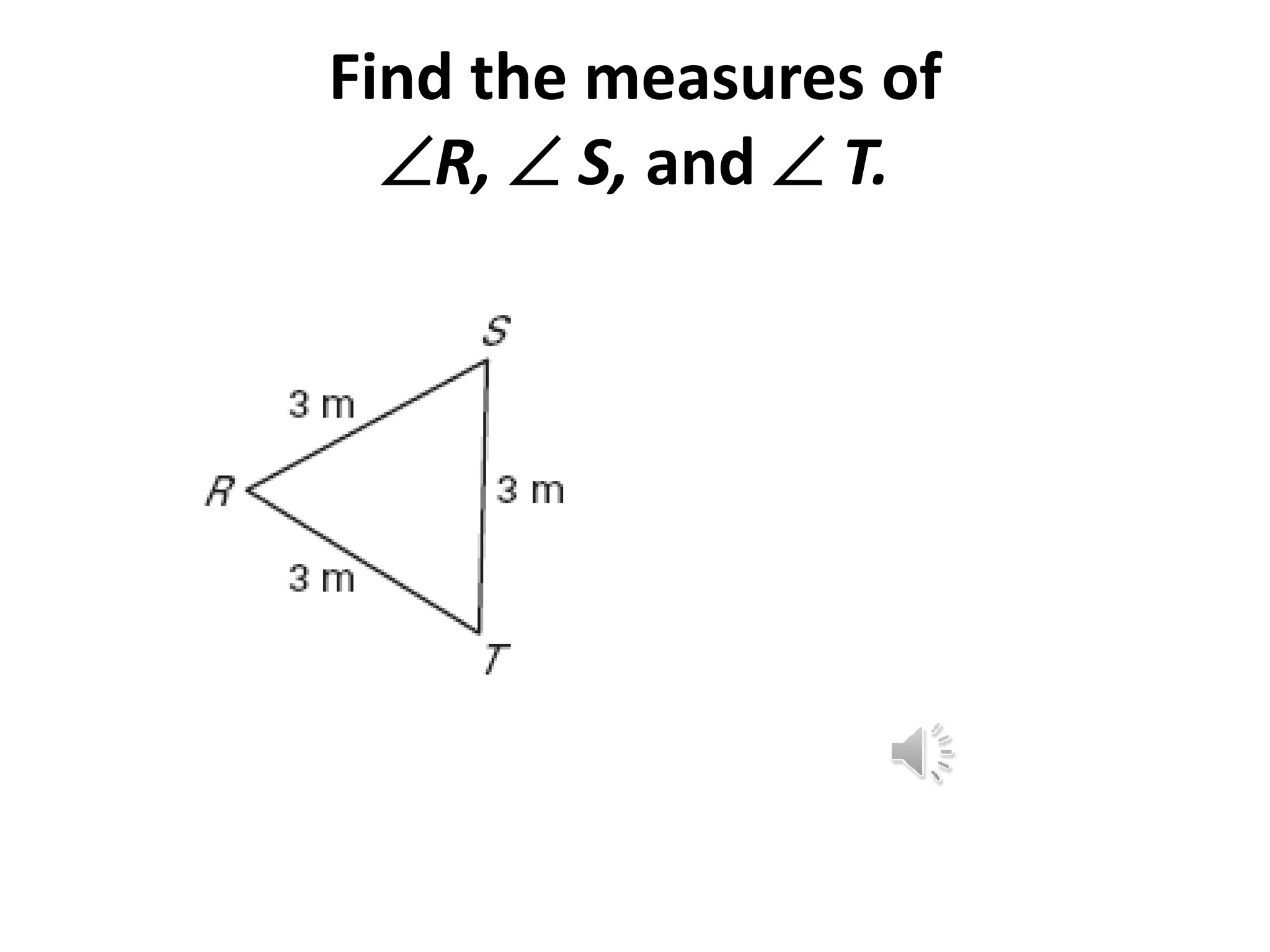
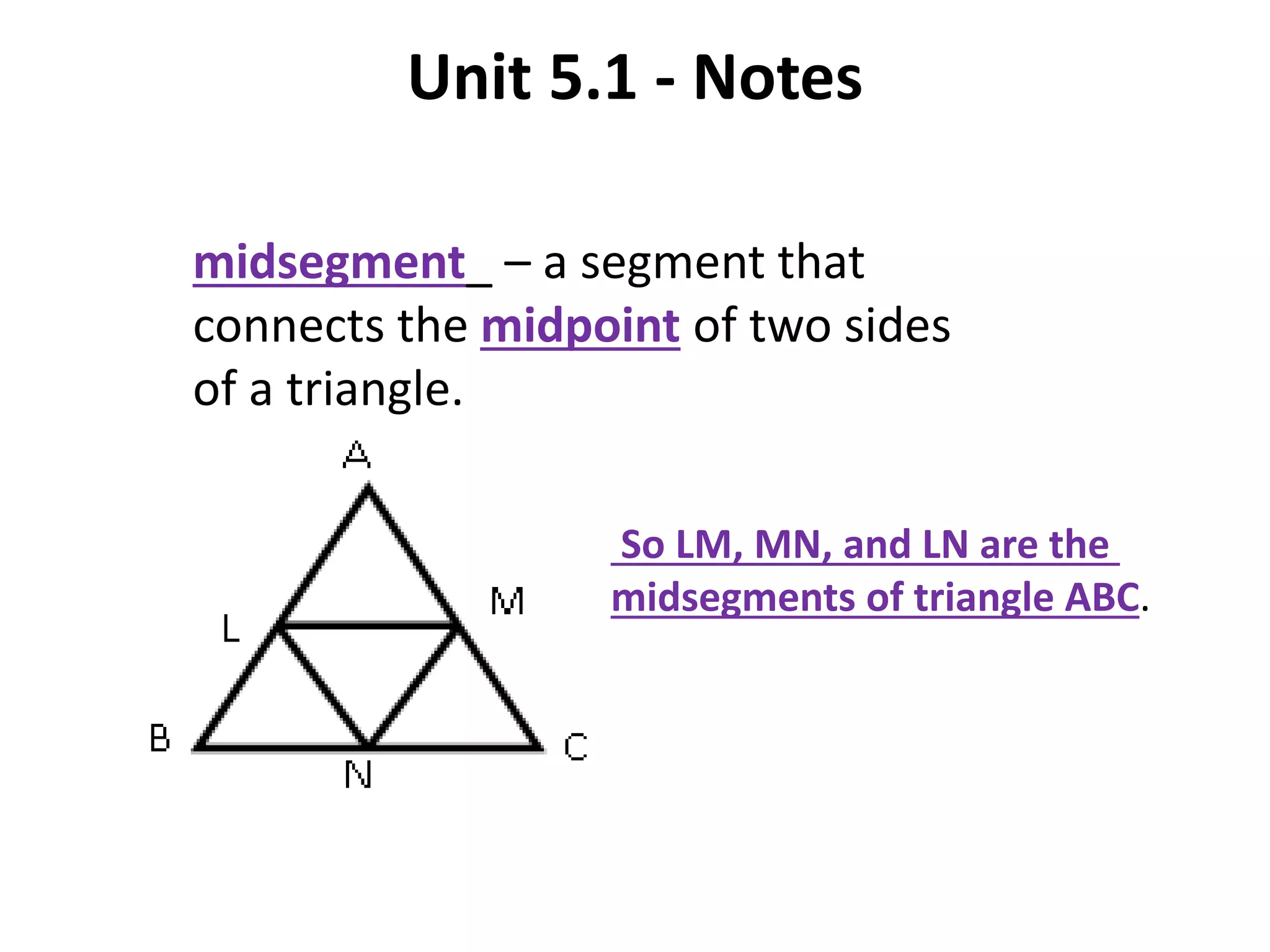
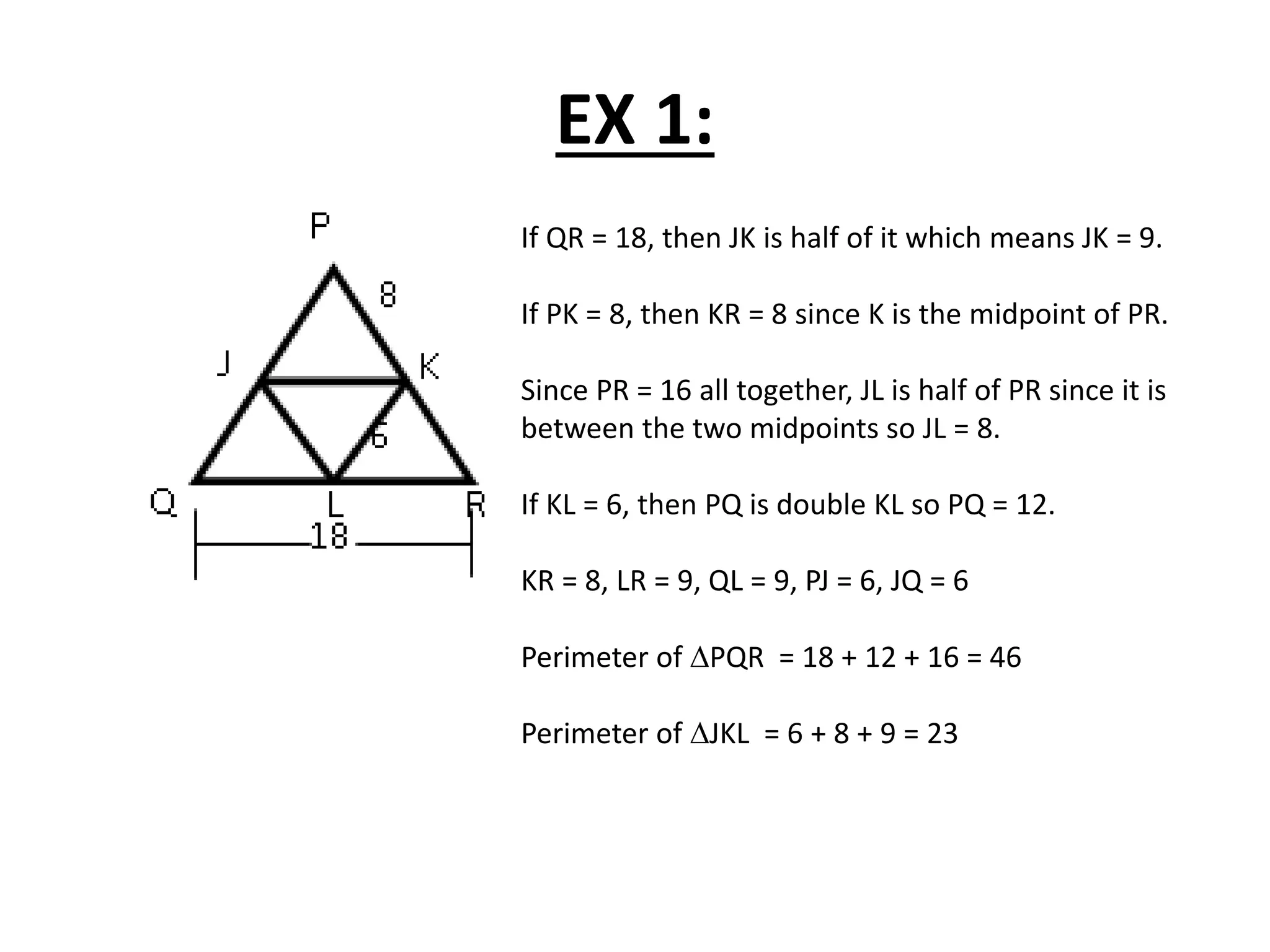
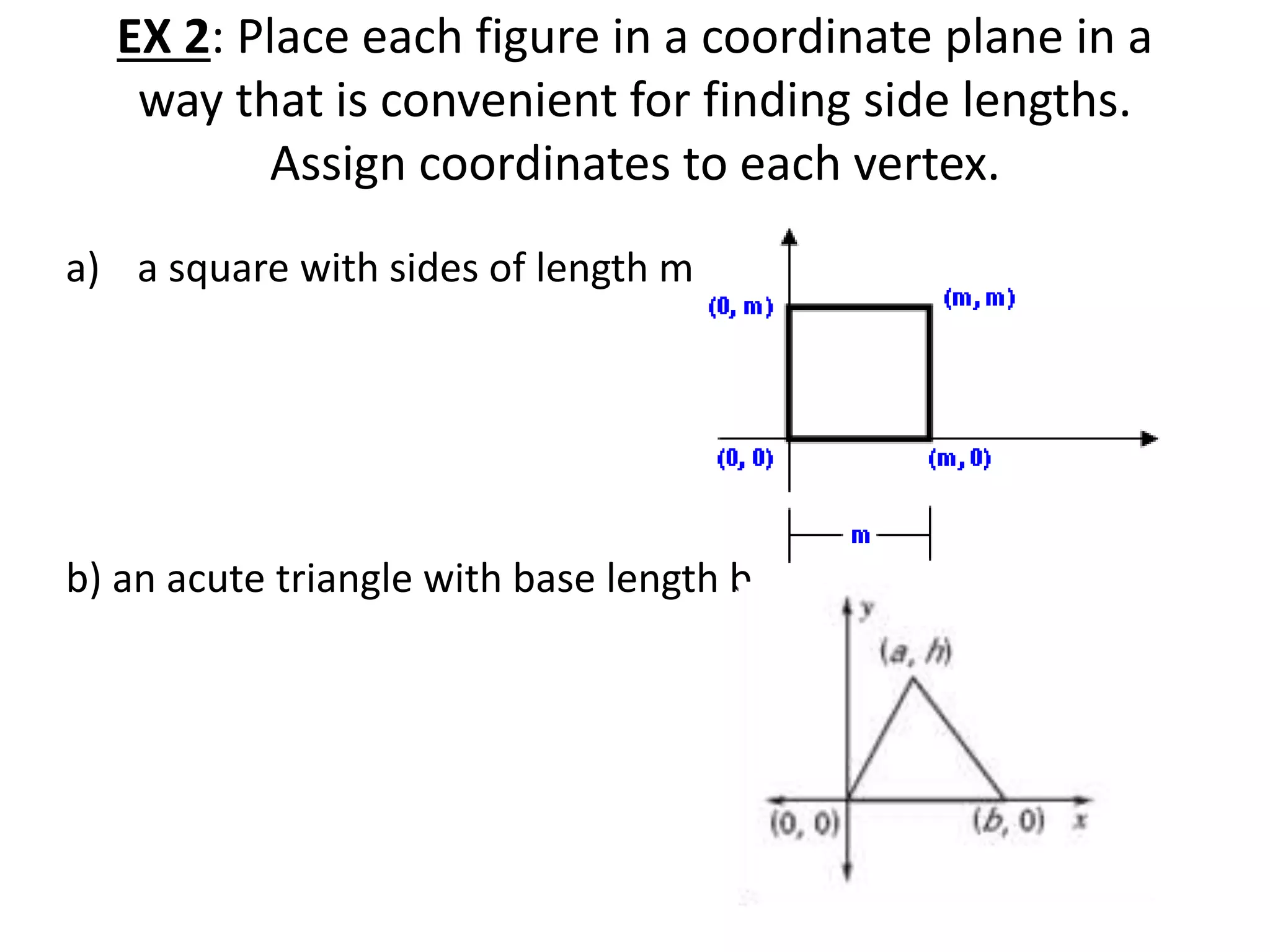
This document contains theorems and examples regarding isosceles and equilateral triangles. Theorem 4.7 states that if two sides of a triangle are congruent, then the angles opposite them are congruent. Theorem 4.8 is the converse of 4.7 - if two angles of a triangle are congruent, then the sides opposite them are congruent. The document then provides examples applying these theorems to find unknown side lengths and angle measures of various triangles. It also introduces the midsegment theorem, which states that the segment connecting the midpoints of two sides of a triangle is parallel to the third side and half its length, along with examples applying this theorem.

1. Section 4.7
Use Isosceles and Equilateral
Triangles

2. THEOREM 4.7: BASE ANGLES
THEOREM
If two sides of a triangle are
congruent, then the angles
opposite them are congruent.
If AB  AC, then B  C

3. THEOREM 4.8: CONVERSE OF BASE
ANGLES THEOREM
If two angles of a triangle
are congruent, then the
sides opposite them are
congruent.
If B  C, then AB  AC.

4. Example 1 Find the unknown
measure.

5. Example 2: Find the value of x.

6. Example 3: Find the values of x and y.

7. Example 4: Find the perimeter of the
triangle.

8. Example 5: Garden You plant a
garden in the shape of a triangle as
shown in the figure. What is the
perimeter

9. Find the measures of
R,  S, and  T.

10. Unit 5.1 - Notes
midsegment_ – a segment that
connects the midpoint of two sides
of a triangle.
So LM, MN, and LN are the
midsegments of triangle ABC.

11. Midsegment Theorem:
The segment connecting the midpoints of two
sides of a triangle is parallel to the third side
and half its length.

12. EX 1:
If QR = 18, then JK is half of it which means JK = 9.
If PK = 8, then KR = 8 since K is the midpoint of PR.
Since PR = 16 all together, JL is half of PR since it is
between the two midpoints so JL = 8.
If KL = 6, then PQ is double KL so PQ = 12.
KR = 8, LR = 9, QL = 9, PJ = 6, JQ = 6
Perimeter of PQR = 18 + 12 + 16 = 46
Perimeter of JKL = 6 + 8 + 9 = 23

13. EX 2: Place each figure in a coordinate plane in a
way that is convenient for finding side lengths.
Assign coordinates to each vertex.
a) a square with sides of length m
b) an acute triangle with base length b