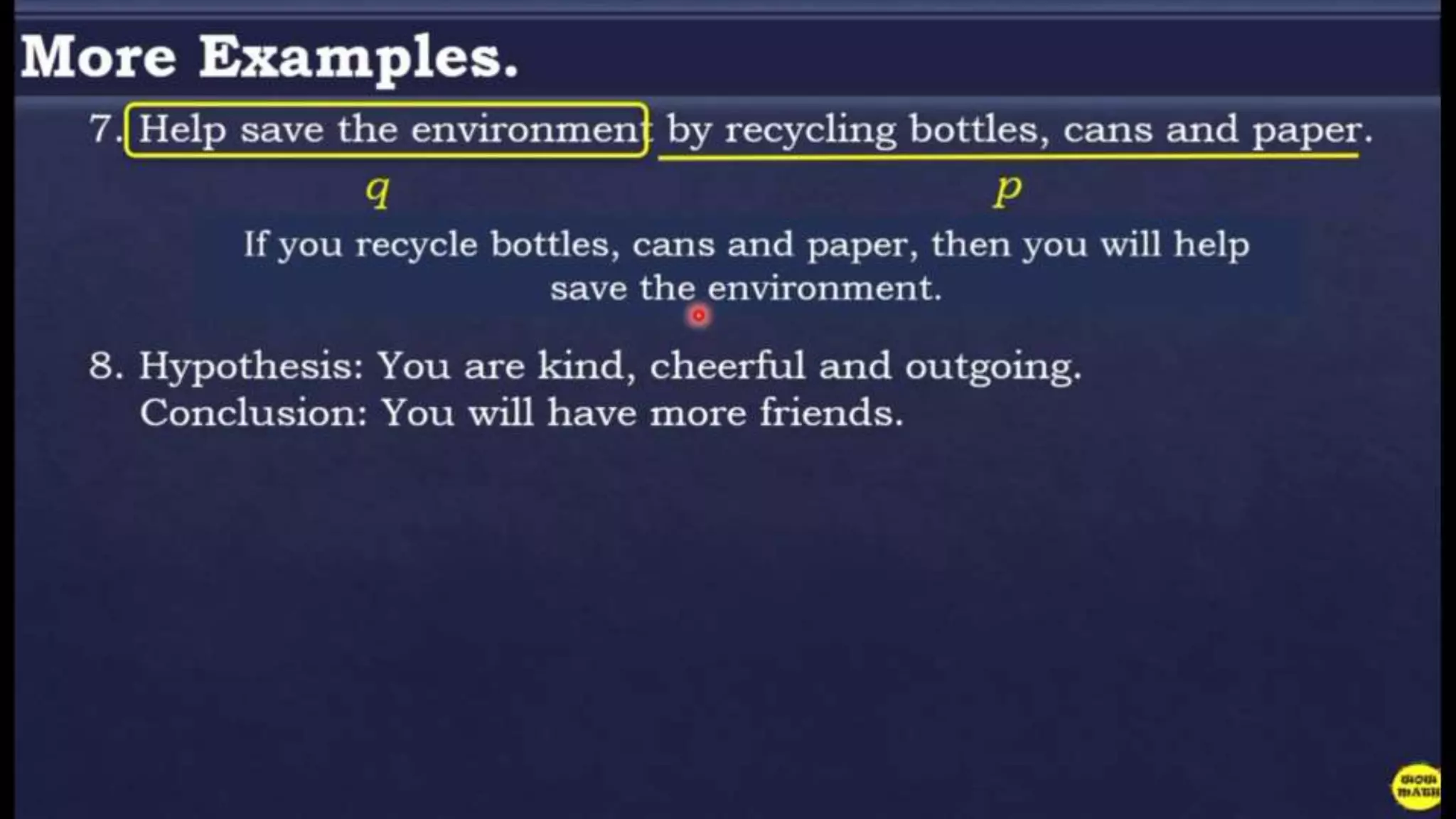
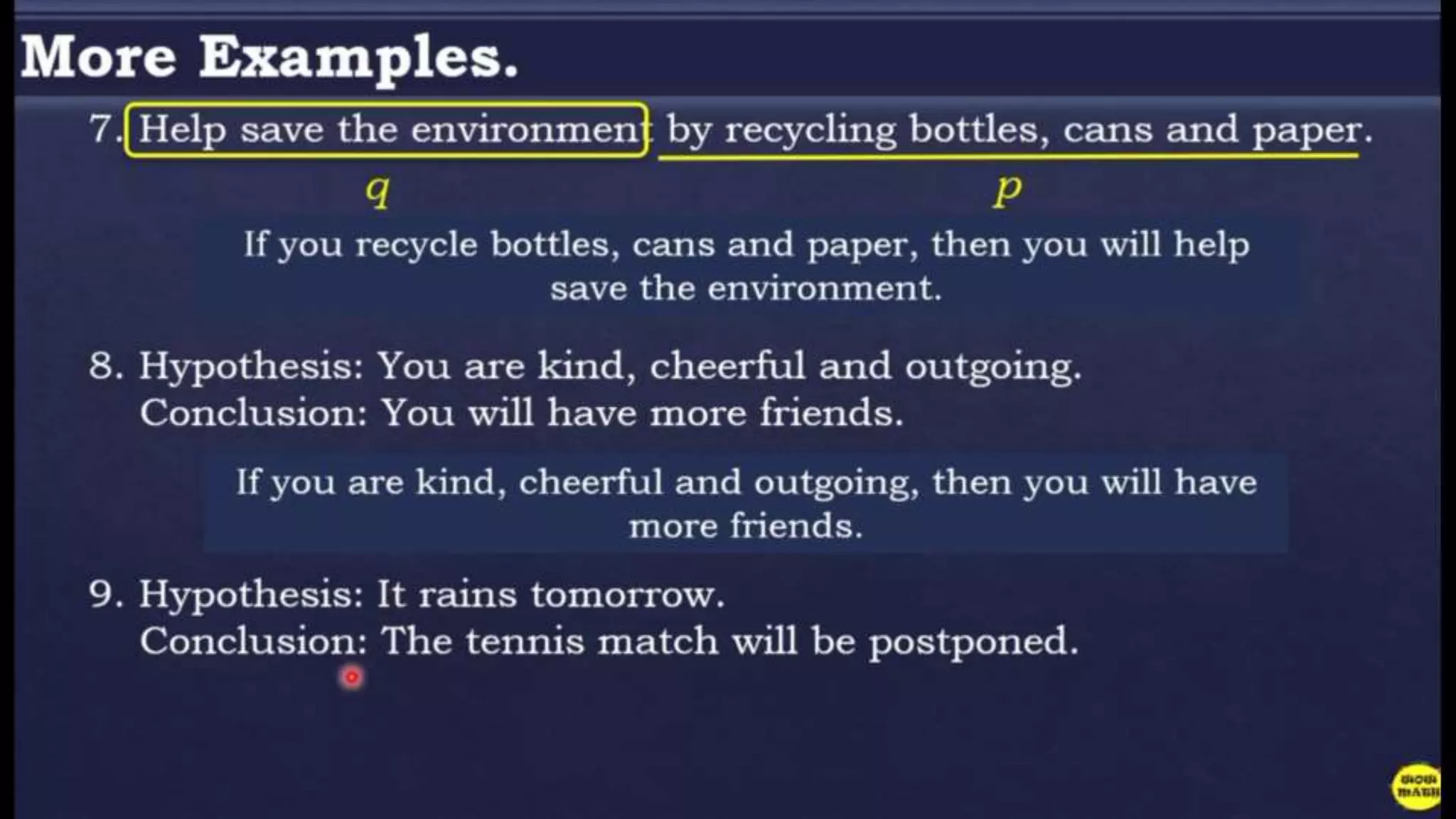
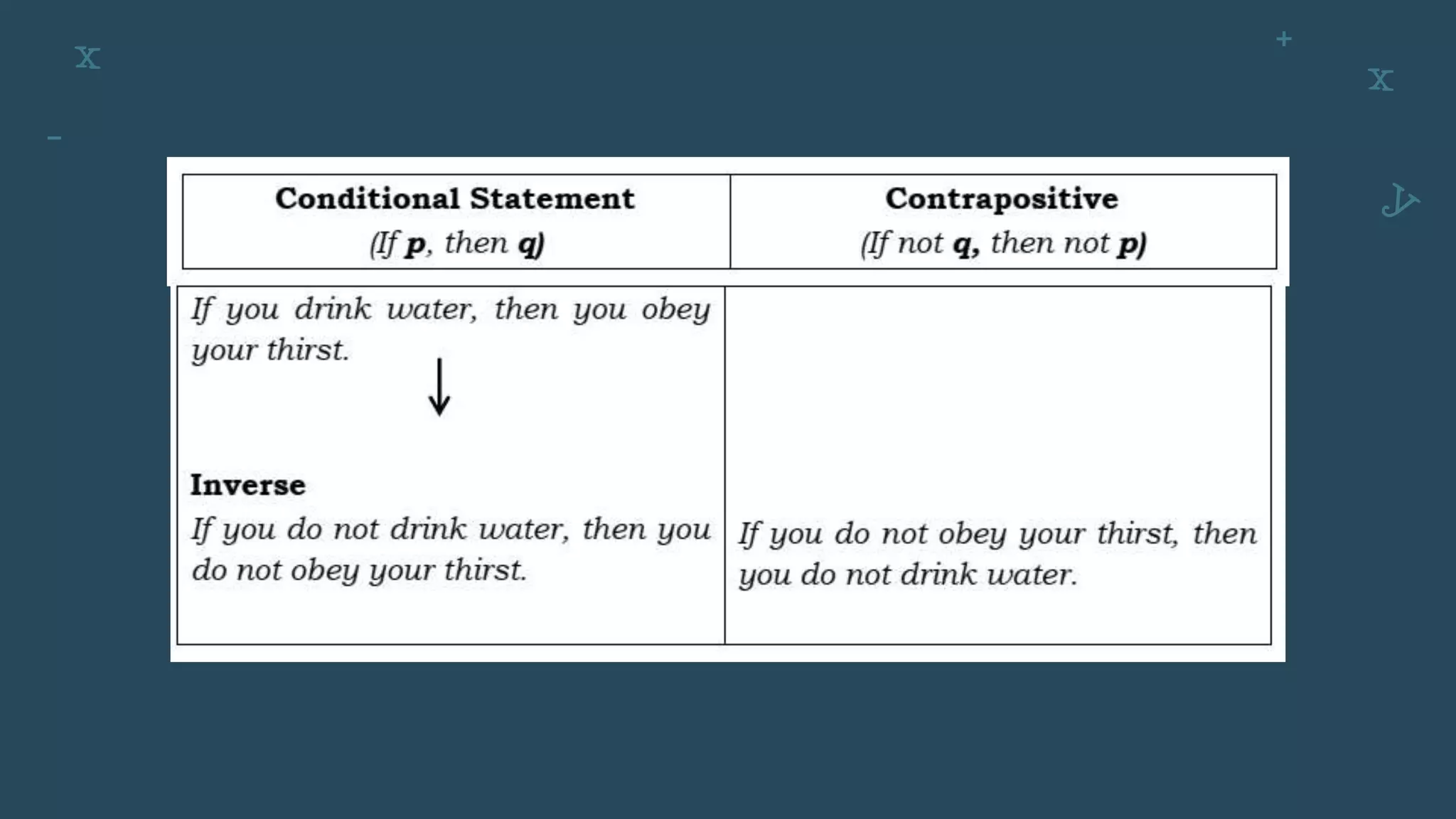
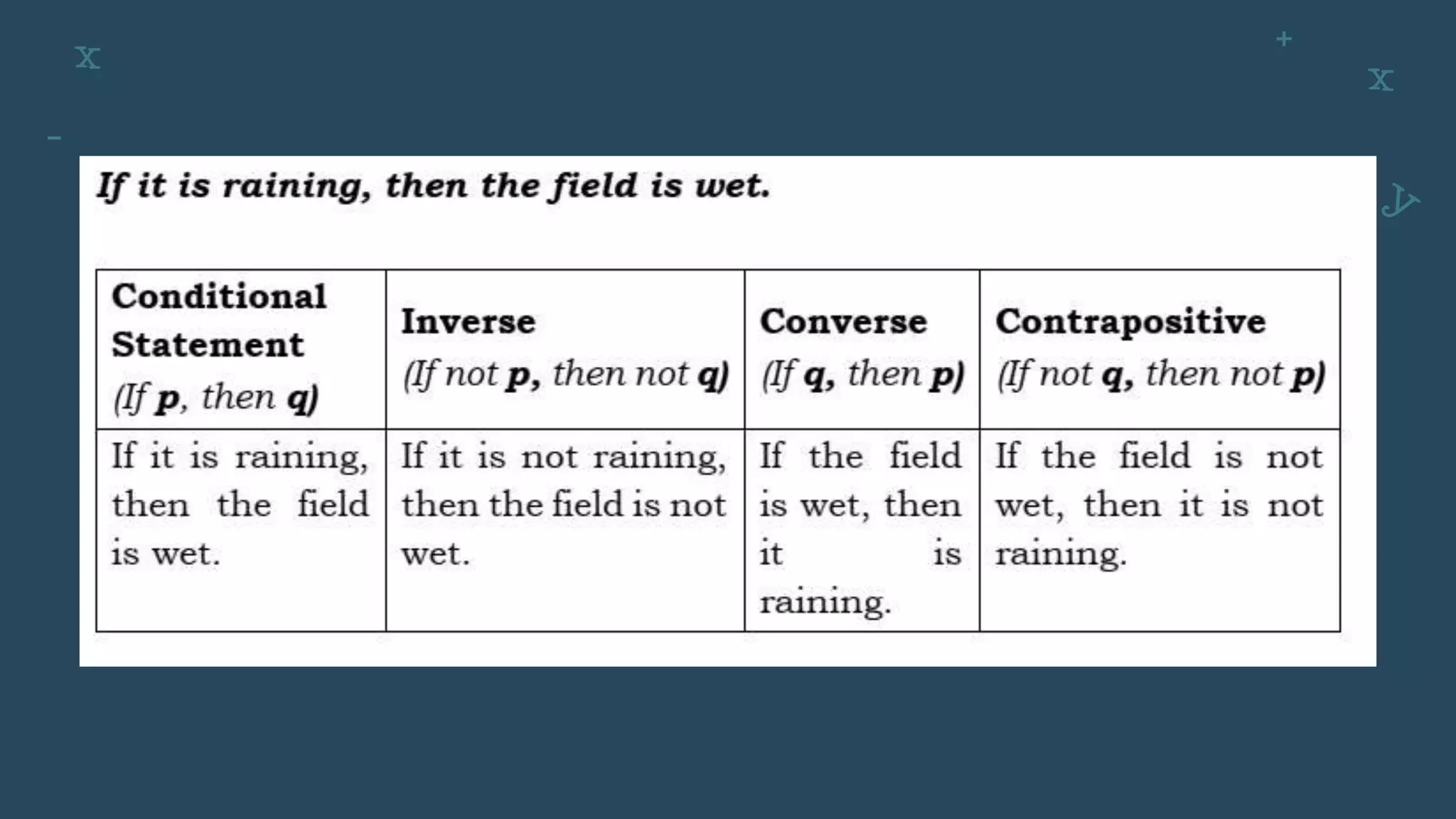
The document discusses conditional statements, also known as if-then statements. It defines conditional statements as having two parts: a hypothesis and a conclusion. The hypothesis is the if part and the conclusion is the then part. It provides examples of writing conditional statements based on given inputs and outputs. It also discusses determining the converse, inverse, and contrapositive of a conditional statement by changing or negating the hypothesis and conclusion.

1. If-then
Statements

2. Conditional Statement
• A logical type of statement that has two parts: a
hypothesis and a conclusion. Conditional can be
written in IF-THEN form.
• A conditional statement is a compound statement of
the form “If p then q“ where p and q are statements.

3. • The first statement, p, is called the hypothesis and
usually begins with if, while the second statement,
q, which usually begins with then is called the
conclusion.
• If HYPOTHESIS, then CONCLUSION.
• If _____________, then ______________.
Hypothesis (p) Conclusion (q)

4. Hypothesis- It states the given facts that are
assumed to be true.
Conclusion- What need to be proven or established.
Implication- is a statement formed by hypothesis and
conclusion.
“If p, then q.” “p q”

5. Let us connect the given input and output
using the if-then form.
Input: I studied for my math test.
Output: I got a good grade.
So, using the if- then statement, the input is the hypothesis of the
statement and the output is the conclusion of the statement.
Answer: If I studied for my math test, then I got a good grade.

6. Let us connect the given input and output
using the if-then form.
Input: It is raining.
Output: We need to use our umbrella.
So, using the if- then statement, the input is the hypothesis of the
statement and the output is the conclusion of the statement.
Answer: If it is raining, then we need to use our umbrella.

7. Example #1
If a number is greater than zero, then the number is
positive.
Hypothesis: The number is greater than zero.
Conclusion: The number is positive.

8. Example #2
If it’s a quadrilateral, then it has four sides.
Hypothesis: It’s a quadrilateral.
Conclusion: It has four sides.

9. Example #3
If 3(n+1) = 6, then n= 1.
Hypothesis: 3(n+1) = 6
Conclusion: n= 1

10. Example #4
Getting enough sleep is good for your health.
Hypothesis: Getting enough sleep
Conclusion: Good for your health.

11. Example #5
An integer that ends in 1,3,5,7 and 9 is an odd
integer.
Hypothesis: An integer that ends in 1,3,5,7 and 9
Conclusion: It is an odd integer

12. Example #6
All prime number are numbers with no other factor
aside from 1 and itself.
Hypothesis: Numbers with no other factor aside
from 1 and itself
Conclusion: It is a prime number

13. Example #7
You have a fever if your body temperature is above
37.6 ℃
Hypothesis: Your body temperature is above 37.6 ℃
Conclusion: You have a fever.

18. Transforming a
Statement
into an
Equivalent If-
then Statement

19. You learned how to identify the hypothesis and
conclusion of a given conditional statement. But
not all conditional statements are written in if-then
form where the hypothesis-conclusion can be
easily identified. In some conditional statements,
conclusions are written before the hypothesis.

35. Determining
the Inverse,
Converse
and
Contrapositiv
e
of an If-then

36. Every conditional statement
has three (3) related
statements and these are
converse, inverse and
contrapositive conditional.

38. Converse
To write the converse of a conditional
statement, simply interchange the
hypothesis and the conclusion. That is, the
then part becomes the if part and the if part
becomes the then part.

39. Inverse
To write the inverse of a conditional
statement, simply negate both the
hypothesis and conclusion.

40. Contrapositive
To form the contrapositive of a conditional
statement, first, get its inverse. Then,
interchange its hypothesis and conclusion.

43. More Examples

44. Converse

47. Biconditional Statement

49. Inverse

50. Contrapositive

51. Exercises

52. Exercises
“A guitar is a musician”

53. Logically Equivalent

56. Directions: Determine the following statement if it is
converse, inverse or contrapositive of the given conditional
(if-then) statement.
Conditional statement: If it’s a right angle, then its
measure is 90 degrees
_________1. If the measure of the angle is 90 degrees, then it is a right
angle.
_________2. If the measure of the angle is not 90 degrees, then it is not
a right angle.
_________3. If the angle is not a right angle, then its measure is not 90
degrees

57. Directions: Determine the following statement if it is
converse, inverse or contrapositive of the given conditional
(if-then) statement.
Conditional statement: If you do your homework,
then you will pass in Mathematics.
_________4. If you do not pass in Mathematics, then you do not do your
homework.
_________5. If you passed in Mathematics, then you did your homework.
_________6. If you do not do your homework, then you will not pass in
Mathematics.

58. For items 7-10, refer to the statement
below.
“If a figure is a square, then it has 4 equal
sides.”
7. What is the hypothesis of the statement?
A. equal sides
B. is a square
C. a figure is a square
D. it has 4 equal sides

59. For items 7-10, refer to the statement
below.
“If a figure is a square, then it has 4 equal
sides.”
8. If a figure is not square, then it doesn’t have 4
equal sides.
A. contrapositive
B. converse
C. if-then
D. inverse

60. For items 7-10, refer to the statement
below.
“If a figure is a square, then it has 4 equal
sides.”
9. If a figure has 4 equal sides, then it is a square.
A. conclusion
B. contrapositive
C. converse
D. inverse

61. For items 7-10, refer to the statement
below.
“If a figure is a square, then it has 4 equal
sides.”
10. If a figure doesn’t have 4 equal sides, then it is
not a square.
A. contrapositive C. hypothesis
B. converse D. inverse