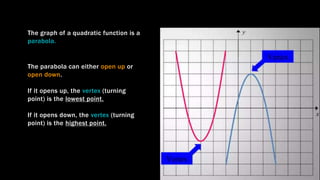
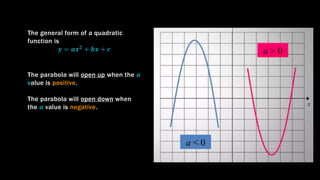
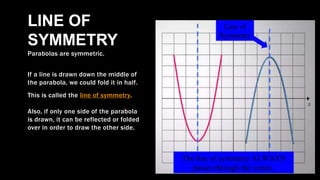
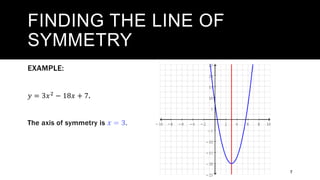
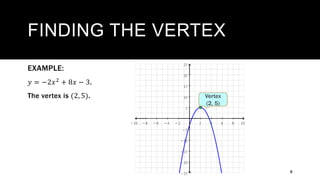
The document discusses key properties of quadratic functions whose general form is y = ax^2 + bx + c. It explains that the graph of a quadratic function is a parabola that can open up or down, with the vertex (lowest/highest point) determining which. It describes how the sign of a determines the direction, and how parabolas are symmetric with a line of symmetry that passes through the vertex. It provides examples of finding the line of symmetry using the formula x = -b/2a and then substituting into the equation to find the y-value of the vertex. Finally, it explains how to transform a quadratic function into vertex form using the method of completing the square.

1. GRAPH OF
QUADRATIC
FUNCTIONS
𝒚 = 𝒂𝒙𝟐 + 𝒃𝒙 + 𝒄

2. SAMPLE FOOTER TEXT
The graph of a quadratic function is a
parabola.
The parabola can either open up or
open down.
If it opens up, the vertex (turning
point) is the lowest point.
If it opens down, the vertex (turning
point) is the highest point.
20XX 2

3. SAMPLE FOOTER TEXT
The general form of a quadratic
function is
𝒚 = 𝒂𝒙𝟐 + 𝒃𝒙 + 𝒄
The parabola will open up when the 𝒂
value is positive.
The parabola will open down when
the 𝒂 value is negative.
20XX 3

4. LINE OF SYMMETRY

5. SAMPLE FOOTER TEXT
Parabolas are symmetric.
If a line is drawn down the middle of
the parabola, we could fold it in half.
This is called the line of symmetry.
Also, if only one side of the parabola
is drawn, it can be reflected or folded
over in order to draw the other side.
20XX 5
LINE OF
SYMMETRY

6. FINDING THE LINE OF
SYMMETRY
6
Given a quadratic
function of the form
𝑦 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐,
the equation of the
line of symmetry is
𝒙 = −
𝒃
𝟐𝒂
EXAMPLE:
Find the axis of symmetry of
𝑦 = 3𝑥2 − 18𝑥 + 7.
Using the formula: 𝒙 = −
𝒃
𝟐𝒂
𝑥 = −
−18
2 3
=
18
6
= 3
Therefore, the axis of symmetry is 𝒙 = 𝟑.
It is illustrated on the next slide.

7. FINDING THE LINE OF
SYMMETRY
7
EXAMPLE:
𝑦 = 3𝑥2
− 18𝑥 + 7.
The axis of symmetry is 𝒙 = 𝟑.

8. FINDING THE VERTEX
8
RECALL:
The line of symmetry always
passes through the vertex.
Thus, the line of symmetry gives
the 𝒙 − 𝒄𝒐𝒐𝒓𝒅𝒊𝒏𝒂𝒕𝒆 of the
vertex.
To get the 𝒚 − 𝒄𝒐𝒐𝒓𝒅𝒊𝒏𝒂𝒕𝒆,
substitute the 𝑥 − 𝑣𝑎𝑙𝑢𝑒 into the
equation.
EXAMPLE:
𝑦 = −2𝑥2
+ 8𝑥 − 3.
Find the axis of symmetry first. 𝒙 = −
𝒃
𝟐𝒂
𝑥 = −
8
2 −2
=
−8
−4
= 2
Substitute 𝒙 = 𝟐 into the equation to find the y
coordinate.
𝑦 = −2 2 2 + 8 2 − 3
= −2 4 + 16 − 3
= 5
Therefore, the vertex is (2, 5).

9. FINDING THE VERTEX
9
EXAMPLE:
𝑦 = −2𝑥2
+ 8𝑥 − 3.
The vertex is (2, 5). Vertex
(2, 5)

10. SAMPLE FOOTER TEXT
VERTEX
FORM OF
A
QUADRATI
C
FUNCTION
10

11. FINDING VERTEX FORM
11
To find the vertex form of a quadratic function, the method of
Completing the Square is used.
Use the link below to watch a video on how this is done.
Vertex Form by Completing the Square

12. FINDING VERTEX FORM
12
Now, let us find the vertex form of the
previous example.
𝑦 = −2𝑥2
+ 8𝑥 − 3
𝑎 = −2, 𝑏 = 8, 𝑐 = −3
Step 1: Group the variables
(−2𝑥2
+8𝑥) − 3
Step 2: Factorize out −2.
−2(𝑥2
− 4𝑥) − 3
Step 3: Create a perfect square
−2 𝑥2
− 4𝑥 + −2 2
− 3 + 2(−2)2
Step 3 cont’d:
−2 𝑥 − (−2) 2
− 3 + 8
= −2 𝑥 − −2
2
+ 5
= −2 𝑥 + 2 2 + 5
The expression is now of the form
𝑎(𝑥 + ℎ)2
+𝑘
This is the vertex form:
𝑦 = −2 𝑥 + 2 2 + 5

13. THE END.
13