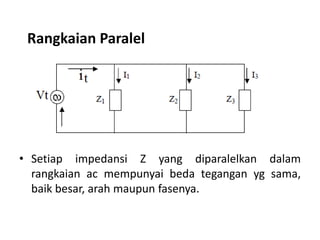
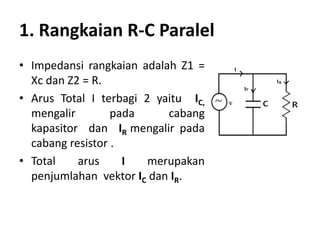
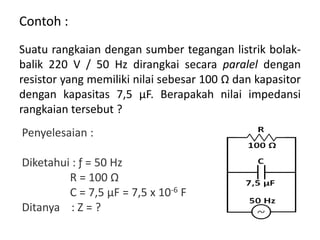
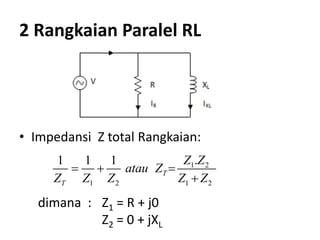
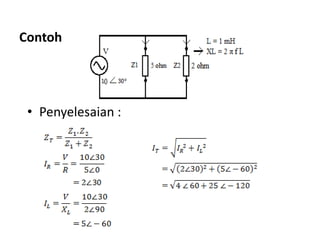
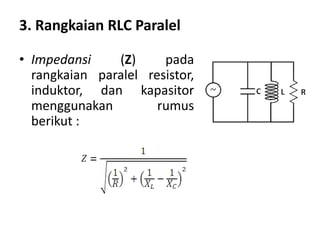
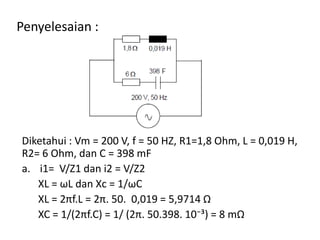
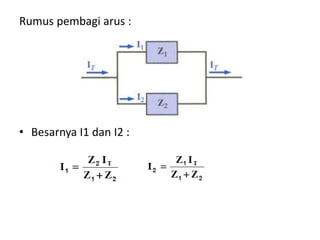
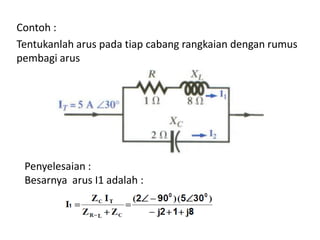
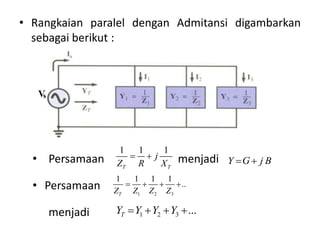
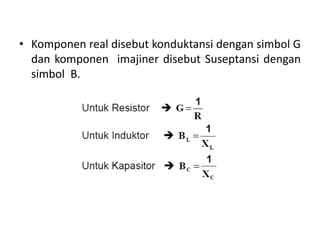
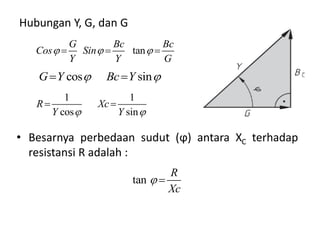
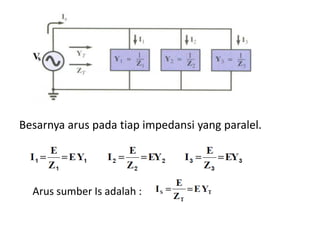
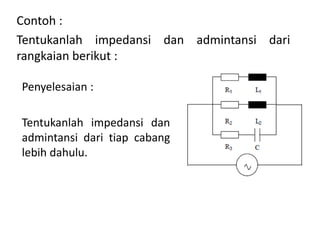
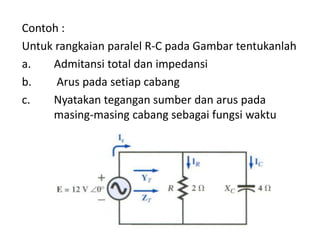
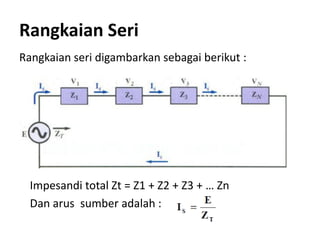
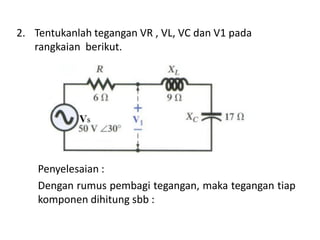
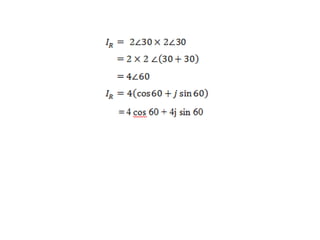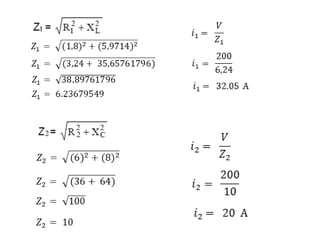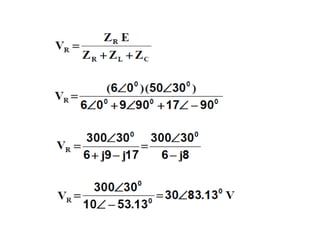Dokumen menjelaskan tentang rangkaian AC paralel yang melibatkan resistor, kapasitor, dan induktor, serta cara menghitung impedansi dan arus total menggunakan hukum Kirchhoff dan hukum Ohm. Terdapat juga contoh perhitungan untuk berbagai konfigurasi rangkaian, termasuk variasi dengan arus bolak-balik. Selain itu, dokumentasi mencakup konsep admitansi sebagai kebalikan dari impedansi dan hubungan di antara komponen dalam rangkaian.

1. Rangkaian AC Pararel
Simon Patabang, MT.
Universitas Atma Jaya Makassar

2. • Setiap impedansi Z yang diparalelkan dalam
rangkaian ac mempunyai beda tegangan yg sama,
baik besar, arah maupun fasenya.
Rangkaian Paralel

3. • Berdasarkan hukum Kirchof I diperoleh besarnya
arus It adalah It = i1 + i2 + i3
• Berdasarkan hukum Ohm, diperoleh persamaan
sebagai berikut It = Vt/ Zt
• Besarnya total impedansi yang paralel adalah :
• Untuk dua impedansi yang dihubungkan paralel,
persamaan menjadi :
tV

4. 1. Rangkaian R-C Paralel
• Impedansi rangkaian adalah Z1 =
Xc dan Z2 = R.
• Arus Total I terbagi 2 yaitu IC,
mengalir pada cabang
kapasitor dan IR mengalir pada
cabang resistor .
• Total arus I merupakan
penjumlahan vektor IC dan IR.

5.  Tegangan pada R dan XC, besarnya sama karena
terhubung paralel yaitu V= Vm sin ω t.
 Arus pada R adalah sefasa dengan tegangan (V).
IR = V/R
 Arus pada cabang Xc adalah IC mendahului tegangan
sebesar 900.
IC = V/XC
 Sedangkan arus total I mendahului tegangan (v)
sebesar sudut φ.
I = IR + Ic

6. • Karena arus yang mengalir melalui resistor
dan kapasitor terjadi perbedaan fasa, untuk
itu hubungan arus (i) dapat ditentukan dengan
menggunakan persamaan kuadrat berikut;
Sehingga :

7. • Oleh karena itu, besarnya arus percabangan yang
mengalir menuju resistor dan kapasitor menentukan
besarnya impedansi (Z) secara keseluruhan dari
rangkaian
dimana
maka

8. • Besarnya perbedaan sudut (φ) antara
reaktansi kapasitif (XC) terhadap resistansi (R)
dapat ditentukan dengan menggunakan
persamaan :
atau

9. Contoh :
Suatu rangkaian dengan sumber tegangan listrik bolak-
balik 220 V / 50 Hz dirangkai secara paralel dengan
resistor yang memiliki nilai sebesar 100 Ω dan kapasitor
dengan kapasitas 7,5 μF. Berapakah nilai impedansi
rangkaian tersebut ?
Penyelesaian :
Diketahui : ƒ = 50 Hz
R = 100 Ω
C = 7,5 μF = 7,5 x 10-6 F
Ditanya : Z = ?

10. • Jawab :
Langkah pertama menghitung nilai reaktansi
kapasitif (XC) pada kapasitor :

11. • Jika nilai XC telah diketahui, selanjutnya menghitung
nilai impedansi (Z) dengan rumus impedansi
dihubungkan secara paralel :

12. 2 Rangkaian Paralel RL
• Impedansi Z total Rangkaian:
1 2
1 2 1 2
.1 1 1
T
T
Z Z
atau Z
Z Z Z Z Z
  

dimana : Z1 = R + j0
Z2 = 0 + jXL

13. • Arus Total Rangkaian :
Arus sumber I terbagi menjadi IR dan IL, jadi
I = IR + IL, dimana :
• Total Tegangan Rangkaian
Tegangan pada R dan XL besarnya sama, yaitu sama
dengan tegangan sumber V.
V = VR = VL  Karena L , R, dan sumber hubungan
paralel.
L R
L
V V
I dan I
X R
 

14. • Berdasarkan grafik di atas, maka diperolah IT adalah:
• Sudut phasa θ dan Z dapat dihitung dengan rumus :
1
, ,XL
R T
I V
tg Z Z Z
I I
   
     
 
2 2
T R XLI I I 

15. • Impedansi Z total :
Nilai Z1 dan Z2 dapat kita cari menggunakan rumus
dibawah ini:
1 2
1 2 1 2
.1 1 1
T
T
Z Z
atau Z
Z Z Z Z Z
  


16. Contoh
• Penyelesaian :

18. 3. Rangkaian RLC Paralel
• Impedansi (Z) pada
rangkaian paralel resistor,
induktor, dan kapasitor
menggunakan rumus
berikut :

19. Arus Total I
• Arus listrik (I) total pada rangkaian paralel resistor,
induktor, dan kapasitor dengan arus bolak-balik
dapat diketahui, jika arus listrik masing-masing pada
beban telah diketahui kemudian menghitung dengan
menggunakan rumus :
I = Arus listrik total pada rangkaian (A)
IR = Arus listrik yang mengalir pada beban resistor (A)
IL = Arus listrik yang mengalir pada beban induktor (A)
IC = Arus listrik yang mengalir pada beban kapasitor (A)

20. Tegangan Total V
• Nilai tegangan (V) pada rangkaian tersebut dapat
dihitung dengan menggunakan rumus yang berasal
sari hasil substitusi rumus hukum ohm :
Keterangan:
V = Tegangan listrik pada rangkaian (Volt)
I = Arus listrik pada rangkaian (A)
Z = Impedansi (Ω)

21. Sudut phasa
• Sudut phasa dapat diketahui dengan menggunakan
rumus berikut :
p
1
cos
R
Z
   
  
 

22. Sifat Rangkaian
1. Bersifat resistif apabila nilai arus listrik yang mengalir
pada induktor sama dengan arus listrik yang mengalir
pada kapasitor IL = IC, arus listrik total se fase dengan
tegangan.
2. Bersifat induktif apabila nilai arus listrik yang
mengalir pada induktor lebih besar dari pada arus
listrik yang mengalir pada kapasitor IL > IC, arus listrik
total tertinggal (Lag) terhadap tegangan.
3. Bersifat kapasitif apabila nilai arus listrik yang
mengalir pada induktor lebih kecil dari pada arus
listrik yang mengalir pada kapasitor IL < IC, arus listrik
total mendahului (lead) terhadap tegangan.

23. Contoh :
1. Suatu sumber tegangan bolak-balik memiliki nilai
frekuensi sebesar 50 Hz, dirangkai secara paralel
dengan beban-bebannya yang berupa resistor 30 Ω,
Induktor 300 mH, dan kapasitor 50 μF. Berapakah
nilai impedansi pada rangkaian tersebut?
Diketahui : f = 50 Hz
R = 30 Ω
L = 300 mH = 0,3 H
C = 50 μF = 5 x 10-5 F
Ditanya : Z =?

24. • Jawab :
Langkah pertama menghitung nilai reaktansi
induktif (XL), dan reaktansi kapasitif (XC) :

25. • Nilai impedansi (Z) total pada rangkaian tersebut :

26. 2. Sebuah Resistor dengan resistansi 8 Ohm dihubung
seri dengan induktansi 0,0191 H kemudian diparalel
dengan kapasitor 398 mF dan resistansi 6 Ohm yang
dihubung seri. Rangkaian disuplay dengan tega-
ngan 200 V, 50 Hz.
Hitunglah:
a. Arus masing-masing cabang.
b. Arus total
c. Sudut fase antara arus dan tegangan

27. Penyelesaian :
Diketahui : Vm = 200 V, f = 50 HZ, R1=1,8 Ohm, L = 0,019 H,
R2= 6 Ohm, dan C = 398 mF
a. i1= V/Z1 dan i2 = V/Z2
XL = ωL dan Xc = 1/ωC
XL = 2πf.L = 2π. 50. 0,019 = 5,9714 Ω
XC = 1/(2πf.C) = 1/ (2π. 50.398. 10⁻³) = 8 mΩ

29. b. Arus total It = ?
It = i1 + i2
c. Sudut fase antara arus dan tegangan
Cos θ1 = R1/Z1
Cos θ1 = 1,8/6,24
Cos θ1 = 0,288462
θ1 = 73,2°
Cos θ2 = R2/Z2
Cos θ2 = 6/10
Cos θ2 = 0,6
θ2 = 53,1°
Z1 dan Z2 paralel maka Z = Z1. Z2 / (Z1 + Z2)

30. 


1,53102,7326,6
1,53102,7326,6 x
Zt
1,53sin101,53cos102,73sin26,62,73cos26,6
3,1266,62
jj
Zt



14807,7
3,1266,62
j
Zt






88,33023,16
3,1266,62
Zt
 42,92907,3Zt
Sudut fase antara arus dan tegangan adalah 92,42°,
bertanda negatip berarti arus terlambat terhadap
tegangan.
 1,53102dan2,7326,61 ZZ
 It = V/Zt  42,9219,51it


31. Rumus pembagi arus :
• Besarnya I1 dan I2 :

32. Contoh :
Tentukanlah arus pada tiap cabang rangkaian dengan rumus
pembagi arus
Penyelesaian :
Besarnya arus I1 adalah :

33. • Arus I2 pada cabang 2 :

34. • Admitansi adalah kebalikan dari impedansi Z. Admitansi
dinyatakan dengan simbol Y dan satuan mho
• Konduktansi adalah kebalikan dari impedansi R.
Admitansi dinyatakan dengan simbol G.
• Suseptansi adalah kebalikan dari impedansi X. Admitansi
dinyatakan dengan simbol B.
Admitansi, Konduktansi, dan Suseptansi
1
Y
Z

1
G
R

1
B
X


35. • Rangkaian paralel dengan Admitansi digambarkan
sebagai berikut :
• Persamaan menjadi
1 1 1
T T
j
Z R X
 
Y G j B 
1 2 3
1 1 1 1
..
TZ Z Z Z
   • Persamaan
menjadi 1 2 3 ...TY Y Y Y   

36. • Komponen real disebut konduktansi dengan simbol G
dan komponen imajiner disebut Suseptansi dengan
simbol B.

37. Hubungan Y, G, dan G
• Besarnya perbedaan sudut (ϕ) antara XC terhadap
resistansi R adalah :
tan
G Bc Bc
Cos Sin
Y Y G
    
cos sinG Y Bc Y  
tan
R
Xc
 
1 1
cos sin
R Xc
Y Y 
 

38. Admitansi untuk tiap elemen impedansi didefinisikan
sebagai berikut :
1. Admitansi Resistor
2. Admitansi Induktor
3. Admitansi Kapasitor

39. Besarnya arus pada tiap impedansi yang paralel.
Arus sumber Is adalah :

40. Contoh :
Tentukanlah impedansi dan admintansi dari
rangkaian berikut :
Penyelesaian :
Tentukanlah impedansi dan
admintansi dari tiap cabang
lebih dahulu.

41. • Cabang 1 terdiri dari R1 dan L1
• Cabang 2 terdiri dari R2 dan L2
• Cabang 3 terdiri dari R3 dan C
Ketiga cabang terhubung paralel maka :
Yt = Y1 + Y2 + Y3

42. Contoh :
Untuk rangkaian paralel R-C pada Gambar tentukanlah
a. Admitansi total dan impedansi
b. Arus pada setiap cabang
c. Nyatakan tegangan sumber dan arus pada
masing-masing cabang sebagai fungsi waktu

43. Penyelesaian :
Total admitansi dan impedansi :

44. Impedansi total adalah :
b. Arus pada tiap admitansi
c. Tegangan sumber dan arus sebagai fungsi waktu

45. Rangkaian Seri
Rangkaian seri digambarkan sebagai berikut :
Impesandi total Zt = Z1 + Z2 + Z3 + … Zn
Dan arus sumber adalah :

46. • Tegangan pada setiap impendansi
Dimana setiap tegangan Vn adalah :
• Rumus pembagi tegangan :
dimana :
Zt = impedansi total
Vx = tegangan yang dicari
E = tegangan sumber rangkaian ac

47. 2. Tentukanlah tegangan VR , VL, VC dan V1 pada
rangkaian berikut.
Penyelesaian :
Dengan rumus pembagi tegangan, maka tegangan tiap
komponen dihitung sbb :

50. Sekian