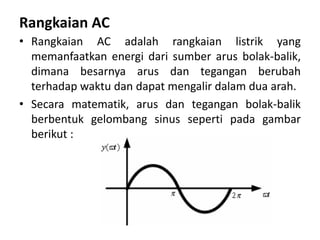
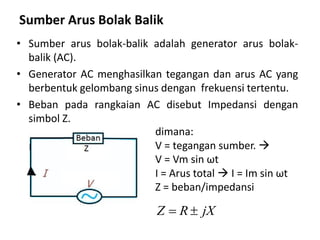
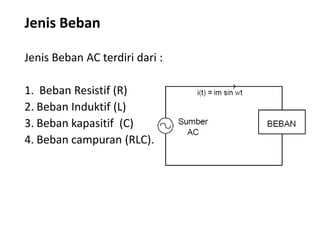
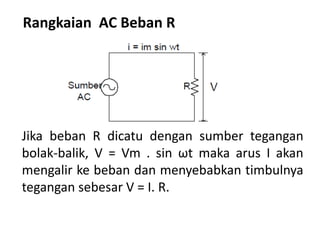
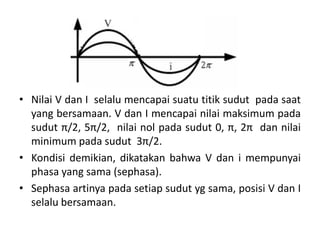
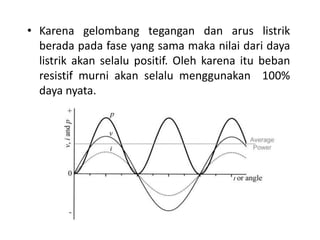
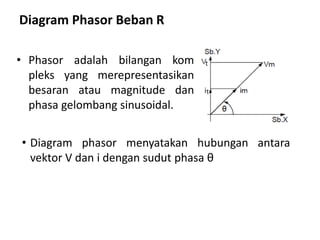
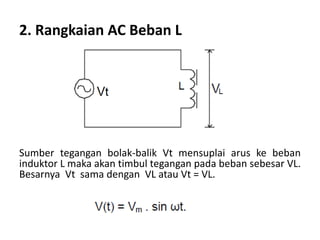
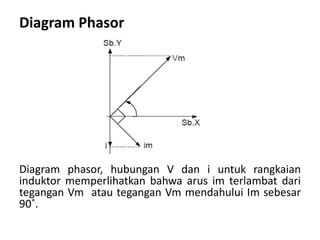
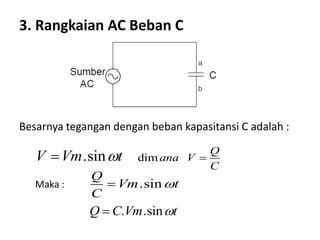
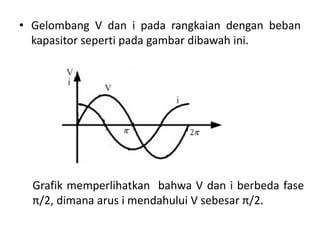
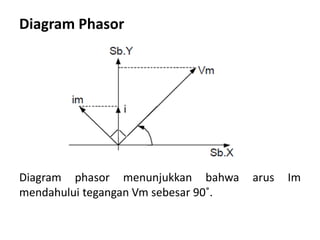
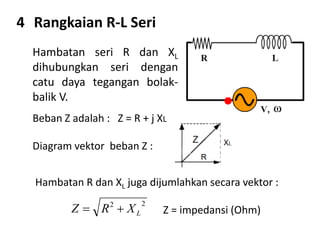
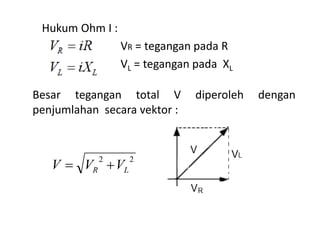
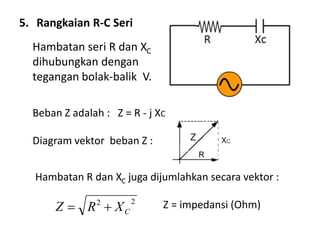
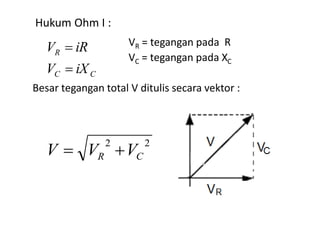
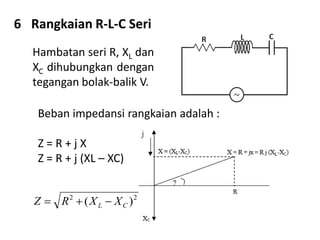
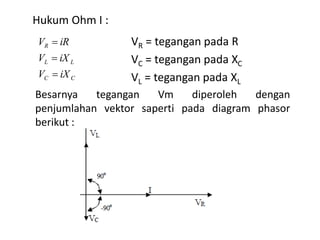
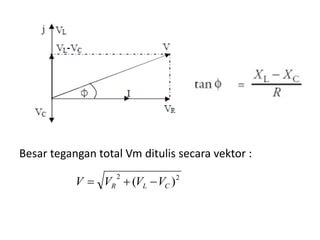
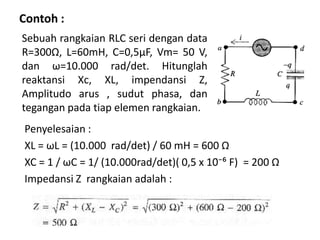
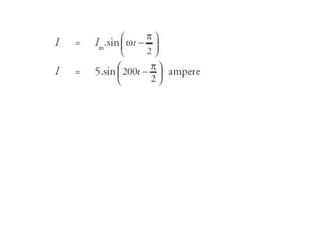Dokumen ini membahas pemanfaatan energi listrik arus bolak-balik (AC), termasuk pengertian beban listrik, rangkaian AC, serta sifat-sifat gelombang arus dan tegangan AC. Ada penjelasan mengenai jenis beban seperti beban resistif, induktif, dan kapasitif, serta persamaan yang berkaitan dengan arus dan tegangan dalam rangkaian tersebut. Terdapat juga contoh soal dan penyelesaian terkait perhitungan dalam rangkaian AC.

1. Pemanfaatan Energi
Sumber Arus Bolak Balik
Simon Patabang, MT.
Universitas Atma Jaya Makassar

2. Pendahuluan
• Pemanfaaan energi listrik AC pada umumnya berupa
beban listrik pada perumahan dan industri.
• Beban listrik adalah besarnya kebutuhan daya listrik yang
harus disuplay oleh pembangkit tenaga listrik kepada
konsumen energi listrik.
• Dalam kehidupan sehari-hari, beban listrik adalah
peralatan yang mengunakan daya listrik agar dapat
bermanfaat bagi manusia.
• Contoh beban listrik dalam rumah tangga diantaranya
televisi, lampu penerangan, setrika, mesin cuci, lemari es
dan lain-lain

3. Rangkaian AC
• Rangkaian AC adalah rangkaian listrik yang
memanfaatkan energi dari sumber arus bolak-balik,
dimana besarnya arus dan tegangan berubah
terhadap waktu dan dapat mengalir dalam dua arah.
• Secara matematik, arus dan tegangan bolak-balik
berbentuk gelombang sinus seperti pada gambar
berikut :

4. Sumber Arus Bolak Balik
• Sumber arus bolak-balik adalah generator arus bolak-
balik (AC).
• Generator AC menghasilkan tegangan dan arus AC yang
berbentuk gelombang sinus dengan frekuensi tertentu.
• Beban pada rangkaian AC disebut Impedansi dengan
simbol Z.
dimana:
V = tegangan sumber. 
V = Vm sin ωt
I = Arus total  I = Im sin ωt
Z = beban/impedansi
Z R jX 

5. • Arus dan tegangan bolak balik didefinisikan dengan
persamaan sebagai berikut :
dimana :
V : tegangan sesaat
I : arus sesaat
Vm : tegangan maksimum
Im : arus maksimum
ω : frekuensi/kecepatan sudut (rad/detik)
t : waktu (detik)
Sudut phasa θ = ω.t rad
Imsin
V Vmsin t
i t





6. Salah satu sifat khusus dari gelombang arus AC adalah
mempunyai sifat periodik atau berulang dengan selang
waktu tertentu yang disebut dengan perioda.
Hubungan antara frekuensi sudut (ω) , frekuensi (f) dan
periode T adalah :
ω = 2πf
f = 1 / T (Hertz,Hz)
Maka ω = 2π/T
T = Periode = waktu untuk satu gelombang

7. Besaran pada tegangan bolak-balik yaitu :
1. Tegangan sesaat (Vt) adalah tegangan pada suatu
waktu (t) detik.
2. Tegangan maksimum (Vm) adalah tegangan dengan
harga maksimum dari tegangan nominal.
3. Tegangan peak to peak (puncak-puncak) (Vpp)
merupakan beda tegangan maksimum dengan
tegangan minimum, dengan persamaan:
Vpp = 2. Vm
Tegangan maksimum dan peak to peak ditunjuk
kan pada pengukuran Osiloscope.

8. 4. Tegangan rata-rata (Vrata-rata) didefinisikan dengan
persamaan :
5. Tegangan efektif (Vef) dirumuskan dengan :
Tegangan efektif ditunjukkan oleh alat ukur
multimeter.

9. Besaran pada Arus bolak-balik yaitu :
1. Arus sesaat (It) adalah arus pada suatu waktu t
detik.
2. Arus maksimum (Vm) adalah arus dengan harga
maksimum dari arus nominal.
3. Arus puncak-puncak (Vpp) merupakan beda arus
maksimum dengan arus minimum, dengan
persamaan:
Ipp = 2. Im

10. 4. Arus rata-rata (Irata-rata) didefinisikan dengan
persamaan :
5. Arus efektif (Ief) adalah dirumuskan dengan :

11. Contoh:
Sebuah generator ac menghasilkan tegangan sebesar Vt =
120 sin 60t volt dan arus it = 40 sin 60t Amper.
Tentukanlah :
1. Tegangan dan arus maksimum
2. Sudut frekuensi
3. Frekuensinya
4. Periodanya
5. Tegangan dan arus rata-rata
6. Tegangan dan arus efektif
7. Tegangan peak to peak

12. Penyelesaian :
Persamaan tegangan Vt = 120 sin 60t volt dan arus it =
40 sin 60t Amper.
1. Tegangan dan arus maksimum
Rumus : Vt = Vm sin wt dan it = Im sin wt.
Dari persamaan diketahui bahwa :
Vm = 120 volt dan Im = 40 A.
2. Sudut frekuensi
Sudut frekuensi w = 60 rad/det

13. 3. Frekuensinya.
 = 2πf  f =  /2π dimana π = 22/7
f = 60/(2.22/7)  f = 9,55 Hz
4. Periodanya
T = 1/f  T = 1/9,55 = 0,105 detik

14. 5. Tegangan dan arus rata-rata
Vr = 2. 120/π = 76,36 Volt
Ir = 2. 40/ π = 25,45 A
6. Tegangan dan arus efektif
Vef = Vm/√2  Vef = 120/√2 = 84,85 Volt
Ief = Im /√2  Ief = 40/√2 = 28,28 A
7. Tegangan peak to peak
Vpp = 2.Vm  Vpp = 2.120 = 240 Volt
dan
2
rata rata
Vm
V
 
2
rata rata
Im
I
 

15. Jenis Beban
Jenis Beban AC terdiri dari :
1. Beban Resistif (R)
2. Beban Induktif (L)
3. Beban kapasitif (C)
4. Beban campuran (RLC).

16. 1. Beban Resistif
• Beban resistif dihasilkan oleh alat-alat listrik yang
bersifat tahanan murni (resistor) seperti pada
elemen pemanas dan lampu pijar.
• Beban resistif ini memiliki sifat yang “pasif”, dimana
ia tidak mampu memproduksi energi listrik, dan
justru menjadi konsumen energi listrik.
• Resistor bersifat menghalangi aliran elektron yang
melewatinya sehingga mengakibatkan terkonver-
sinya energi listrik menjadi panas.

17. Rangkaian AC Beban R
Jika beban R dicatu dengan sumber tegangan
bolak-balik, V = Vm . sin ωt maka arus I akan
mengalir ke beban dan menyebabkan timbulnya
tegangan sebesar V = I. R.

18. dimana Im = Vm/R, Im (arus maksimum), maka :
Gambar gelombang tegangan dan arus bolak-balik
pada beban R digambarkan sebagai berikut :
Besarnya arus listrik yang mengalir pada beban R
adalah :
ImsinI t

19. • Nilai V dan I selalu mencapai suatu titik sudut pada saat
yang bersamaan. V dan I mencapai nilai maksimum pada
sudut π/2, 5π/2, nilai nol pada sudut 0, π, 2π dan nilai
minimum pada sudut 3π/2.
• Kondisi demikian, dikatakan bahwa V dan i mempunyai
phasa yang sama (sephasa).
• Sephasa artinya pada setiap sudut yg sama, posisi V dan I
selalu bersamaan.

20. Sudut Fase dan Beda Fase
• Dalam rangkaian listrik arus bolak-balik sudut
fase dan beda fase akan memberikan informasi
tentang tegangan dan arus.
• Beda fase antara tegangan dan arus bolak-balik
memberikan informasi tentang sifat beban dan
penyerapan energi listrik.
• Dengan mengetahui beda fase antara tegangan
dan arus, maka dapat diketaui sifat beban apakah
resistif, induktif atau kapasitif.

21. • Karena gelombang tegangan dan arus listrik
berada pada fase yang sama maka nilai dari daya
listrik akan selalu positif. Oleh karena itu beban
resistif murni akan selalu menggunakan 100%
daya nyata.

22. Diagram Phasor Beban R
• Phasor adalah bilangan kom
pleks yang merepresentasikan
besaran atau magnitude dan
phasa gelombang sinusoidal.
• Diagram phasor menyatakan hubungan antara
vektor V dan i dengan sudut phasa θ

23. Diagram phasor mempunyai ketentuan sebagai berikut:
a. Panjang phasor menyatakan nilai-nilai maksimum
dari tegangan dan arus bolak-balik, yakni Vm dan
im.
b. Proyeksi phasor terhadap sumbu Y menyatakan
nilai-nilai sesaat dari tegangan (Vt) dan arus bolak-
balik (It), yaitu :
.sin Im.sinVt Vm t dan It t  

24. Pada beban R, sudut phasa arus dan tegangan sama
dengan Nol artinya vektor tegangan dan arus selalu
berimpit.
Sudut phasa artinya beda sudut antara posisi vektor
tegangan dan vektor arus.
Persamaan V dan I dapat dituliskan dalam bentuk polar
sebagai berikut :
/_

25. Contoh :
Rangkaian AC beban R, dimana R = 40Ω, Vm = 100 V, dan
frekuensi generator f = 50 Hz. Pada saat t=0 detik, tegangan
pada resistor VR = 0. Tentukan:
a. arus maksimum,
b. frekuensi sudut ,
c. arus melalui resistor pada t = 1/75 s
d. arus melalui resistor pada t = 1/150 s
Penyelesaian:
Diketahui :
R = 40Ω, Vm = 100 V, f = 50 Hz, VR = 0 , pada saat t=0 detik

26. a. Rangkaian resistor murni, Im dapat dicari dengan
persamaan:
Im = Vm/R = 100/40 = 2,5 A
b. Frekuensi sudut anguler (ω)
ω = 2. π .f = 2. π .50 = 100 π
c. Untuk rangkaian resistor murni, tegangan sefase
dengan arus, sehingga untuk V = Vm.sin ωt, maka I
= Im.sin ωt. Persamaan arus sesaat yaitu:
I(t) = Im.sin ωt = 2,5 sin ωt
pada saat t = 1/75 detik, maka arus It adalah :

27. d. Pada saat t = 1/150 detik, maka arus It adalah :

28. 2. Rangkaian AC Beban L
Sumber tegangan bolak-balik Vt mensuplai arus ke beban
induktor L maka akan timbul tegangan pada beban sebesar VL.
Besarnya Vt sama dengan VL atau Vt = VL.

29. Apabila induktor mempunyai induktansi sebesar L,
maka berdasarkan Hukum Lenz besarnya tegangan
beban adalah :
Karena VL = Vt maka :
L
di
V L
dt

.sin
sin
di
L Vm t
dt
Vm
di t dt
L




Rumus dasar Integral:

30. Jadi arus AC pada beban induktor adalah:
Dgn Integrasi maka besarnya i adalah :
Dimana - cost ωt = sin (ωt - π/2) dan
ωL adalah besarnya hambatan pada induktor disebut
reaktansi induktif dengan simbol XL.
LfLXL .2.    LXVm Im
sin ( cos )
Vm Vm
i t dt i t
L L
 

   
Imsin ( )
2
i t

 
Im
Vm
L


31. Gelombang V dan i dalam rangkaian induktor L
digambarkan sebagai berikut :
Pada saat mencapai nilai maksimum, V berada pada sudut
π/2 sedangkan I mencapai nilai maksimum pada sudut π.
Beda kedua sudut adalah π - π/2 = π/2 (beda sudut fase).
Jadi V dan i berbeda fase sebesar π/2 atau 90 derajat
dimana arus terlambat (lagging) dari tegangan.

32. Diagram Phasor
Diagram phasor, hubungan V dan i untuk rangkaian
induktor memperlihatkan bahwa arus im terlambat dari
tegangan Vm atau tegangan Vm mendahului Im sebesar
90˚.

33. Pada beban induktor L, arus tertinggal terhadap
tegangan sebesar 90˚. Keadaan ini disebut lagging.
maka persamaan tegangan sesaatnya :
Jika persamaan tegangan sesaatnya adalah :
maka persamaan arus sesaat adalah :

34. Jika arusnya adalah :
Maka :
Bentuk polar dari persamaan arus dan tegangan
adalah :

35. Sebuah induktor 0,2 henry dipasang pada sumber
tegangan arus bolak-balik, V = (200. sin 200t) volt.
Tentukan persamaan arus yang mengalir pada
rangkaian tersebut!
Diketahui:
V = (200 sin 200t) volt
L = 0,2 H
Ditanya: I = ... ?
Contoh :

36. Penyelesaian :
V = Vm.sinωt
V = 200.sin 200t
Dari persamaan diketahui :
Vm = 200 volt dan ω= 200 rad/s, maka:
XL = ω.L= (200)(0,2)
XL = 40Ω
Im = Vm / XL = 200 / 40 = 5 A
Untuk beban L, arus tertinggal π/2rad terhadap
tegangan, sehingga:

38. 3. Rangkaian AC Beban C
Besarnya tegangan dengan beban kapasitansi C adalah :
Maka :
.sinV Vm t dim
Q
ana V
C

.sin
Q
Vm t
C

. .sinQ C Vm t

39. Besarnya arus listrik i pada kapasitor adalah :
dq
i
dt
 . .sinQ C Vm tdimana
 . .sin
cos
d C Vm t
i
dt
i C Vm t

 


Jika persamaan Q diturunkan terhadap t maka
diperoleh :
sin( )
2
i C Vm t

  
dimana cos ωt = sin(ωt + π/2), maka persamaan
arus pada beban C adalah :

40. • Besarnya hambatan pada kapasitor disebut reaktansi
kapasitif Xc dengan satuan Ohm yang didefinisikan :
m
m
I
1
I
1
m
m m
CV
V V
Xc
Xc C
C




   
 
 
 
CfC
XC
.2
1
.
1


maka :
mI sini tBentuk dasar persamaan I adalah :

41. Gelombang Arus dan Tegangan
• Persamaan tegangan :
• Persamaan Arus :
.sinV Vm t
sin( )
2
Vm
i t
Xc

 
• Kedua persamaan memperlihatkan beda fasa sebesar
90 derajat dimana arus mendahului tegangan.

42. • Gelombang V dan i pada rangkaian dengan beban
kapasitor seperti pada gambar dibawah ini.
Grafik memperlihatkan bahwa V dan i berbeda fase
π/2, dimana arus i mendahului V sebesar π/2.

43. Diagram Phasor
Diagram phasor menunjukkan bahwa arus Im
mendahului tegangan Vm sebesar 90˚.

44. Pada beban kapasitor, arus mendahului tegangan
sebesar 90˚. Keadaan ini disebut arus leading.
Jika persamaan arus sesaat adalah :
maka persamaan tegangan sesaatnya :
Jika persamaan tegangan sesaatnya adalah :
maka persamaan arus sesaat adalah :

45. Bentuk Polar persamaan arus dan tegangan :

46. Contoh :
Sebuah kapasitor 50 μF dihubungkan dengan sumber
tegangan arus bolak-balik. Arus yang mengalir pada
rangkaian adalah I = (4.sin 100t) A. Tentukanlah
persamaan tegangan pada kapasitor ! Gambarkan
gelombang arus I dan V.
Diketahui:
C = 50 μF = 5 × 10-5 F
I = (4.sin 100t) A
Ditanyakan : Persamaan tegangan, V = ...?

47. Penyelesaian:
I = (Im.sin ω ) A
I = (4.sin100t) A
maka, Im = 4 A, dan ω = 100 rad/s

48. Dari persamaan di atas, maka diperoleh :

49. 4 Rangkaian R-L Seri
Hambatan seri R dan XL
dihubungkan seri dengan
catu daya tegangan bolak-
balik V.
Beban Z adalah : Z = R + j XL
Diagram vektor beban Z :
Hambatan R dan XL juga dijumlahkan secara vektor :
Z = impedansi (Ohm)
22
LXRZ 

50. 22
LR VVV 
Besar tegangan total V diperoleh dengan
penjumlahan secara vektor :
Hukum Ohm I :
VR = tegangan pada R
VL = tegangan pada XL

51. Kuat arus yg mengalir pada rangkaian adalah :
22
LXR
V
Z
V
i


Contoh :
Sebuah Induktor L = 40 mH dan resistor R = 6 Ohm
dirangkai seri dan dihubungkan dengan sebuah
sumber tegangan AC dengan nilai Vm = 200 Volt
dan frekuensi f= 100/π Hz. Tentukanlah kuat arus
melalui rangkaian pada saat t = 0,05 sekon !

52. Terlebih dahulu kita cari beberapa besaran berikut:
Arus maksimum yang mengalir adalah :
Sudut fase antara tegangan dan arus adalah :

53. Subsitusi hasil perhitungan ke dalam persamaan arus,
maka besarnya arus yang mengalir dalam rangkaian
pada saat t=0,05 detik adalah :

54. 5. Rangkaian R-C Seri
Hambatan seri R dan XC
dihubungkan dengan
tegangan bolak-balik V.
Beban Z adalah : Z = R - j XC
Diagram vektor beban Z :
Hambatan R dan XC juga dijumlahkan secara vektor :
Z = impedansi (Ohm)22
CXRZ 

55. VR = tegangan pada R
VC = tegangan pada XC
Besar tegangan total V ditulis secara vektor :
CC
R
iXV
iRV


22
CR VVV 
Hukum Ohm I :

56. Kuat arus i yg mengalir pada rangkaian adalah :
22
CXR
V
Z
V
i


Contoh :
Sebuah kapasitor dengan kapasitas 25/π μF disusun seri
dengan sebuah resistor 300 Ohm dan dihubungkan
dengan sumber tegangan AC dengan persamaan V = 40
sin(100πt) volt. Tentukan arus yang mengalir pada
rangkaian pada saat t = 0,05 sekon.

57. Diketahui :
R=300 Ohm, C= 25/π μF, t = 0,05 detik.
Ditanyakan arus I=?
Jawab :
Persamaan arus I = Im sin(ωt + θ)
Arus maksimum yang mengalir dapat dicari sbb:

58. Sudut fase antara tegangan dan arus dapat dihitung
dari grafik :
 Θ = 53 ͦ
Subsitusi nilai2 yang diperoleh ke dalam persamaan
arus I sbb :
I = Im sin (ωt + θ)

59. Latihan
Sebuah resistor 200 Ω dan kapasitor 5μF dihubungkan seri.
Tegangan pada resistor adalah Vr = 1,2 cos 2500 t Volt.
Tnetukanlah :
a. Persamaan arus
b. Reaktansi kapasitf kapasitor
c. Tegangan pada kapasitor
Penyelesaian :
R dan C dihubungkan seri, maka arus pada R dan C sama
besarnya yaitu : I = VR/R
i= (1,2 cos 2500 t)/ 200 = 6x 10⁻³ cos 2500 t A

60. b. Xc = 1/ωC  Xc = 1/ (2500. 5 x10⁻⁶ )
Xc = 80 Ω.
c. Vc = I. Xc  Vc = 6x 10⁻³ cos 2500 t x 80 Volt . Pada saat t=0
detik maka :
Vc = 6x 10⁻³ x 80 = 0,48 Volt

61. 6 Rangkaian R-L-C Seri
Hambatan seri R, XL dan
XC dihubungkan dengan
tegangan bolak-balik V.
Beban impedansi rangkaian adalah :
Z = R + j X
Z = R + j (XL – XC)
22
)( CL XXRZ 

62. VR = tegangan pada R
VC = tegangan pada XC
VL = tegangan pada XL
Besarnya tegangan Vm diperoleh dengan
penjumlahan vektor saperti pada diagram phasor
berikut :
CC
LL
R
iXV
iXV
iRV



Hukum Ohm I :

63. Besar tegangan total Vm ditulis secara vektor :
22
)( CLR VVVV 

64. Kuat arus yg mengalir pada rangkaian ini adalah :
22
)( CL XXR
V
Z
V
i



65. Contoh :
Penyelesaian :
XL = ωL = (10.000 rad/det) / 60 mH = 600 Ω
XC = 1 / ωC = 1/ (10.000rad/det)( 0,5 x 10̄⁻⁶ F) = 200 Ω
Impedansi Z rangkaian adalah :
Sebuah rangkaian RLC seri dengan data
R=300Ω, L=60mH, C=0,5μF, Vm= 50 V,
dan ω=10.000 rad/det. Hitunglah
reaktansi Xc, XL, impendansi Z,
Amplitudo arus , sudut phasa, dan
tegangan pada tiap elemen rangkaian.

66. Dengan amplitudo tegangan sumber V= 50 volt, maka
amplitudo arus adalah :
Sudut phasa adalah :
Karena sudut phasa positif, maka tegangan
mendahului arus sebesar 53 ͦ.
Tegangan pada R : 
Tegangan L : 

67. Soal Latihan
1. Arus listrik PLN yang sampai ke rumah mempunyai
tegangan 220 V dan frekuensi 50 Hz. Tentukan:
(a) Tegangan maksimum.
(b) Kecepatan sudut.
(c) Tegangan efektif.
2. Sebuah rangkaian ac kapasitif mempunyai frekwensi
sudut 100 rad/s dan Vm = 220 V, Jika C = 20 μF,
tentukanlah kuat arus yang melalui rangkaian pada
saat t = 0,004 s!

68. 3. Suatu kumparan dengan induktansi diri 100 mH dan
hambatan tidak diketahui dan sebuah kapasitor 1 μF di susun
seri dengan suatu osilator berfrekuensi 5000 rad/s. Jika sudut
fase antara tegangan power suplai dan kuat arus 60o ,
tentukan hambatan kumparan.
4. Tegangan induksi pada suatu generator mempunyai
persamaan, Vt = 200 sin(100t )
Tentukan:
a. Tegangan maksimum
b. Kecepatan sudut
c. Frekuensi putaran
d. Periode
e. Lukiskan grafik ggl (tegangan) sebagai fungsi waktu.

69. Sekian