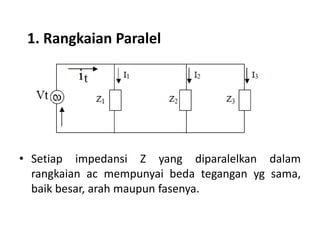
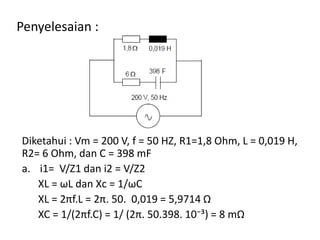
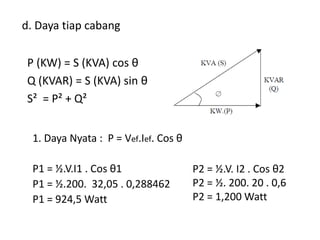
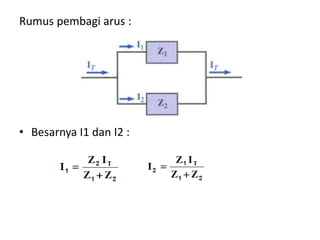
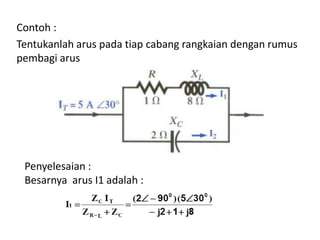
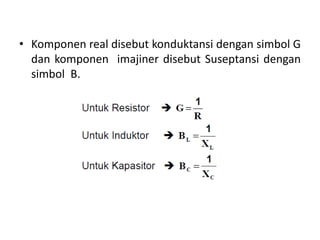
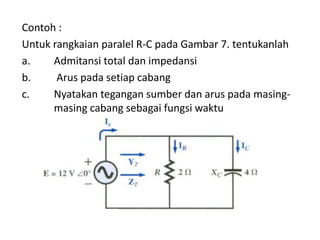
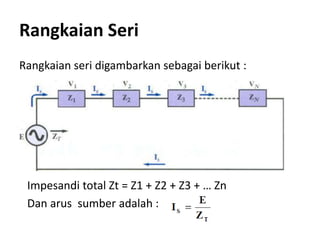
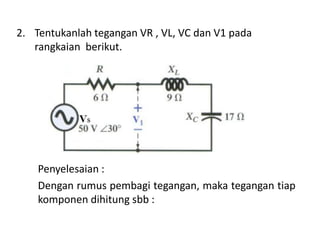
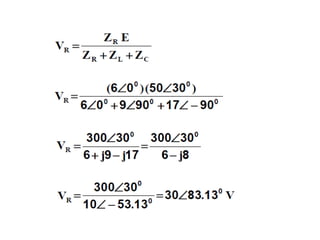Dokumen tersebut membahas tentang rangkaian listrik AC paralel dan seri. Rangkaian paralel memiliki tegangan yang sama pada setiap impedansi, sedangkan arus total pada rangkaian paralel didapat dari penjumlahan arus setiap cabang. Rangkaian seri memiliki arus yang sama pada setiap impedansi, sedangkan tegangan total setara dengan jumlah tegangan setiap cabang. Dokumen ini juga menjelaskan tentang admitansi, impedansi, dan

1. Rangkaian AC Pararel dan Seri
Simon Patabang, ST., MT.
Universitas Atma Jaya Makassar

2. • Setiap impedansi Z yang diparalelkan dalam
rangkaian ac mempunyai beda tegangan yg sama,
baik besar, arah maupun fasenya.
1. Rangkaian Paralel

3. • Berdasarkan hukum Kirchof diperoleh besarnya arus
It adalah It = i1 + i2 + i3
• Berdasarkan hukum Ohm, diperoleh persamaan
sebagai berikut It = Vt/ Zt
• Besarnya total impedansi diperoleh dengan
persamaan :
• Untuk dua impedansi yang dihubungkan paralel,
persamaan menjadi :
tV

4. 1. Sebuah Resistor dengan resistansi 8 Ohm dihubung
seri dengan induktansi 0,0191 H kemudian diparalel
dengan kapasitor 398 mF dan resistansi 6 Ohm yang
dihubung seri. Rangkaian disuplay dengan tega-
ngan 200 V, 50 Hz.
Hitunglah:
a. Arus masing-masing cabang.
b. Arus total
c. Sudut fase antara arus dan tegangan
d. Daya masing-masing cabang
Contoh :

5. Penyelesaian :
Diketahui : Vm = 200 V, f = 50 HZ, R1=1,8 Ohm, L = 0,019 H,
R2= 6 Ohm, dan C = 398 mF
a. i1= V/Z1 dan i2 = V/Z2
XL = ωL dan Xc = 1/ωC
XL = 2πf.L = 2π. 50. 0,019 = 5,9714 Ω
XC = 1/(2πf.C) = 1/ (2π. 50.398. 10⁻³) = 8 mΩ

7. b. Arus total It = ?
It = i1 + i2
It = 32,05 + 20 = 52,05 A
c. Sudut fase antara arus dan tegangan
Cos θ1 = R1/Z1
Cos θ1 = 1,8/6,24
Cos θ1 = 0,288462
θ1 = 73,2°
Cos θ2 = R2/Z2
Cos θ2 = 6/10
Cos θ2 = 0,6
θ2 = 53,1°
Z1 dan Z2 paralel maka Z = Z1. Z2 / (Z1 + Z2)

8. 


1,53102,7326,6
1,53102,7326,6 x
Zt
1,53sin101,53cos102,73sin26,62,73cos26,6
3,1266,62
jj
Zt



14807,7
3,1266,62
j
Zt






88,33023,16
3,1266,62
Zt
 42,92907,3Zt
Sudut fase antara arus dan tegangan adalah 92,42°,
bertanda negatip berarti arus terlambat terhadap
tegangan.
 1,53102dan2,7326,61 ZZ
 It = V/Zt  42,9219,51it


9. 1. Daya Nyata : P = Vef.Ief. Cos θ
P1 = ½.V.I1 . Cos θ1
P1 = ½.200. 32,05 . 0,288462
P1 = 924,5 Watt
P2 = ½.V. I2 . Cos θ2
P2 = ½. 200. 20 . 0,6
P2 = 1,200 Watt
d. Daya tiap cabang
P (KW) = S (KVA) cos θ
Q (KVAR) = S (KVA) sin θ
S² = P² + Q²

10. 2. Daya Reaktif : Q = ½.V.I. sin θ
sin θ1 = XL/Z1
Sin θ1 = 5,9714/6,24
Sin θ1 = 0,956955
Q1 = ½.V.I1 . Sin θ1
Q1 = ½. 200. 32,05 . 0,956955
Q1 = 3.067 VAR
Sin θ2 = XC/Z2
Sin θ2 = 0,008/10
Sin θ2 = 0,0008
Q2 = ½. V. I2 . SIn θ2
Q2 = ½. 200. 20 . 0,008
Q2 = 1,6 VAR

11. 3. Daya Semu : S² = P² + Q²
P1 = 924,5 Watt , Q1 = 3.067 VAR
S1² = P1² + Q1²  S1² = (924,5) ² + (3.067)²
S1 = 3.203,309 VA
P2 = 1,200 Watt , Q2 = 1,6 VAR
S2² = P2² + Q2²  S2² = (1,200) ² + (1,6)²
S2 = 1200,001 VA

12. Rumus pembagi arus :
• Besarnya I1 dan I2 :

13. Contoh :
Tentukanlah arus pada tiap cabang rangkaian dengan rumus
pembagi arus
Penyelesaian :
Besarnya arus I1 adalah :

14. • Arus I2 pada cabang 2 :

15. Admitansi dan Suseptansi
• Kebalikan dari impedansi (Z) disebut admitansi
dengan simbol Y dengan persamaan Y = 1/Z.
• Admitansi dinyatakan dalam satuan mho (kebalikan
dari ohm).
• Persamaan admitansi untuk rangkaian pararel
didefinisikan sbb : Yt = Y1 + Y2 + Y3 + .... Yn
• Impedansi terdiri dari 2 komponen yaitu resistansi
dan Reaktansi dengan persamaan Z = R + jX
sedangkan Admitansi terdiri dari suseptansi G dan
konduktansi B dengan persamaan Y = G + jB.

16. • Komponen real disebut konduktansi dengan simbol G
dan komponen imajiner disebut Suseptansi dengan
simbol B.

17. • Rangkaian paralel dengan Admitansi digambarkan
sebagai berikut :

18. Admitansi untuk tiap elemen impedansi didefinisikan
sebagai berikut :
1. Admitansi Resistor
2. Admitansi Induktor
3. Admitansi Kapasitor

19. Besarnya arus pada tiap impedansi yang paralel.
Arus sumber Is adalah :
Contoh :
Tentukanlah impedansi dan
admintansi dari rangkaian berikut :
Penyelesaian :
Tentukanlah impedansi dan
admintansi dari tiap cabang
lebih dahulu.

20. • Cabang 1 terdiri dari R1 dan L1
• Cabang 2 terdiri dari R2 dan L2
• Cabang 3 terdiri dari R3 dan C
Ketiga cabang terhubung paralel maka :
Yt = Y1 + Y2 + Y3

21. Contoh :
Untuk rangkaian paralel R-C pada Gambar 7. tentukanlah
a. Admitansi total dan impedansi
b. Arus pada setiap cabang
c. Nyatakan tegangan sumber dan arus pada masing-
masing cabang sebagai fungsi waktu

22. Penyelesaian :
Total admitansi dan impedansi :

23. Impedansi total adalah :
b. Arus pada tiap admitansi
c. Tegangan sumber dan arus sebagai fungsi waktu

24. Rangkaian Seri
Rangkaian seri digambarkan sebagai berikut :
Impesandi total Zt = Z1 + Z2 + Z3 + … Zn
Dan arus sumber adalah :

25. • Tegangan pada setiap impendansi
Dimana setiap tegangan Vn adalah :
• Rumus pembagi tegangan :
dimana :
Zt = impedansi total
Vx = tegangan yang dicari
E = tegangan sumber rangkaian ac

26. 2. Tentukanlah tegangan VR , VL, VC dan V1 pada
rangkaian berikut.
Penyelesaian :
Dengan rumus pembagi tegangan, maka tegangan tiap
komponen dihitung sbb :

29. Sekian