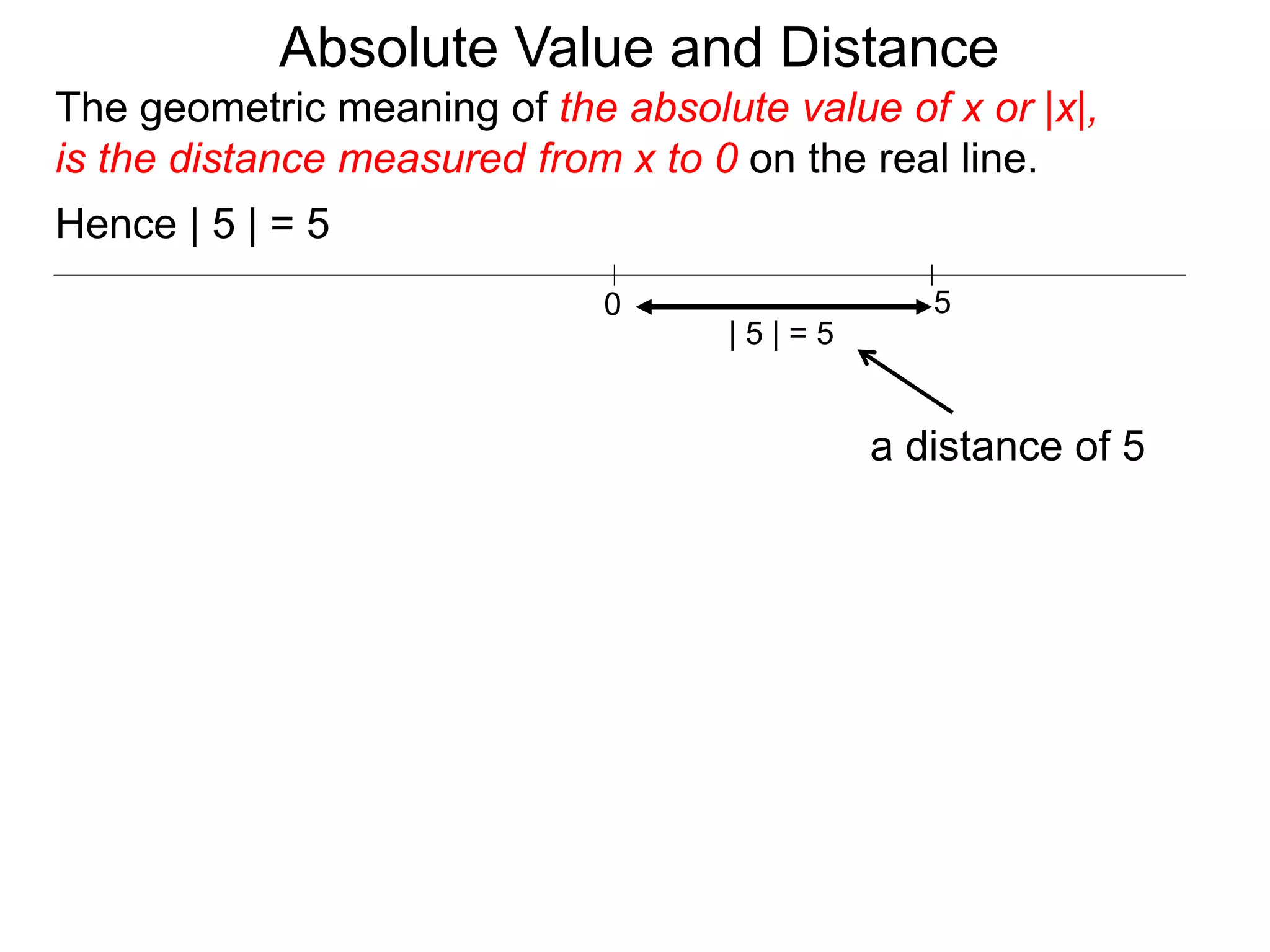
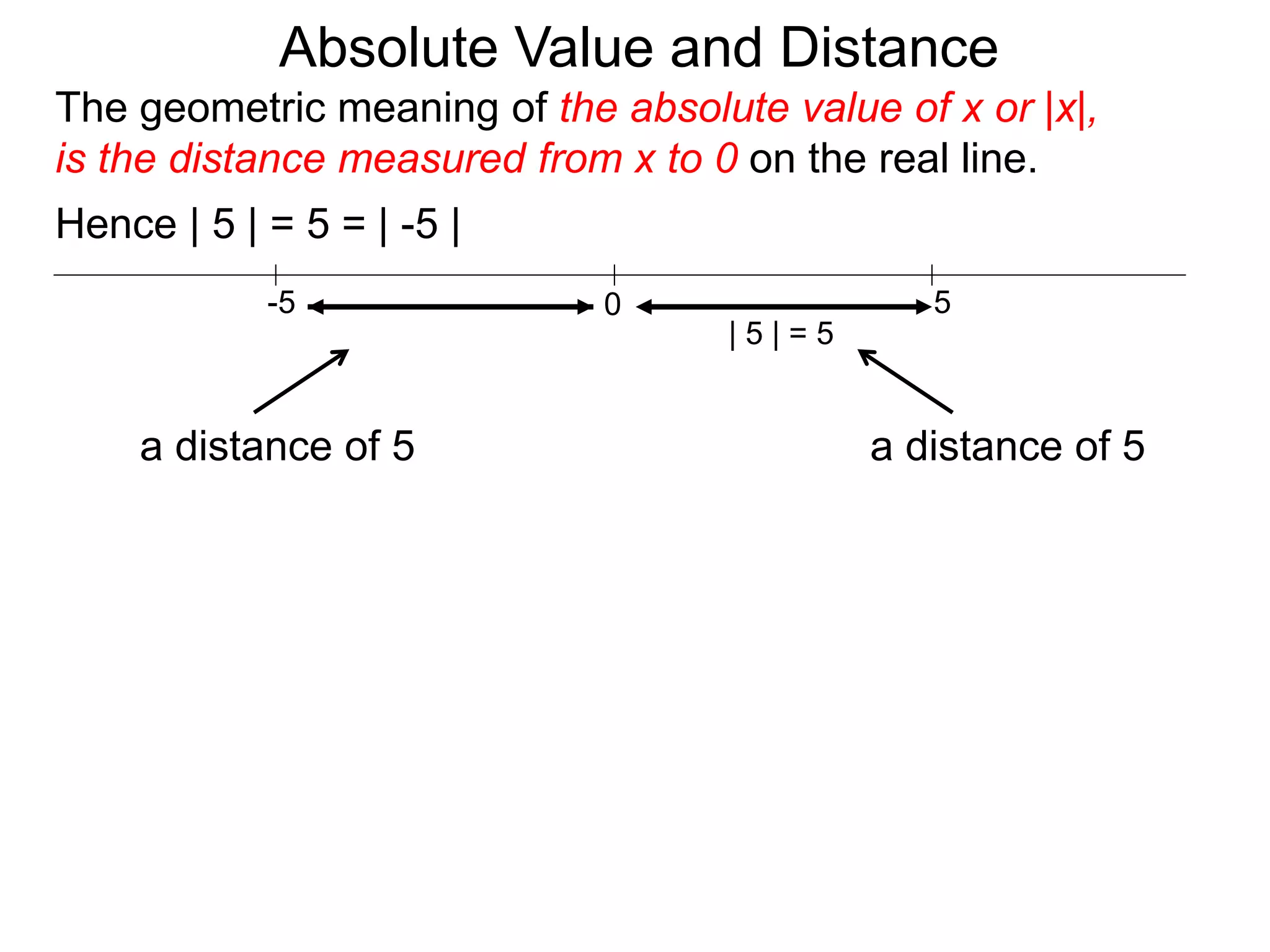
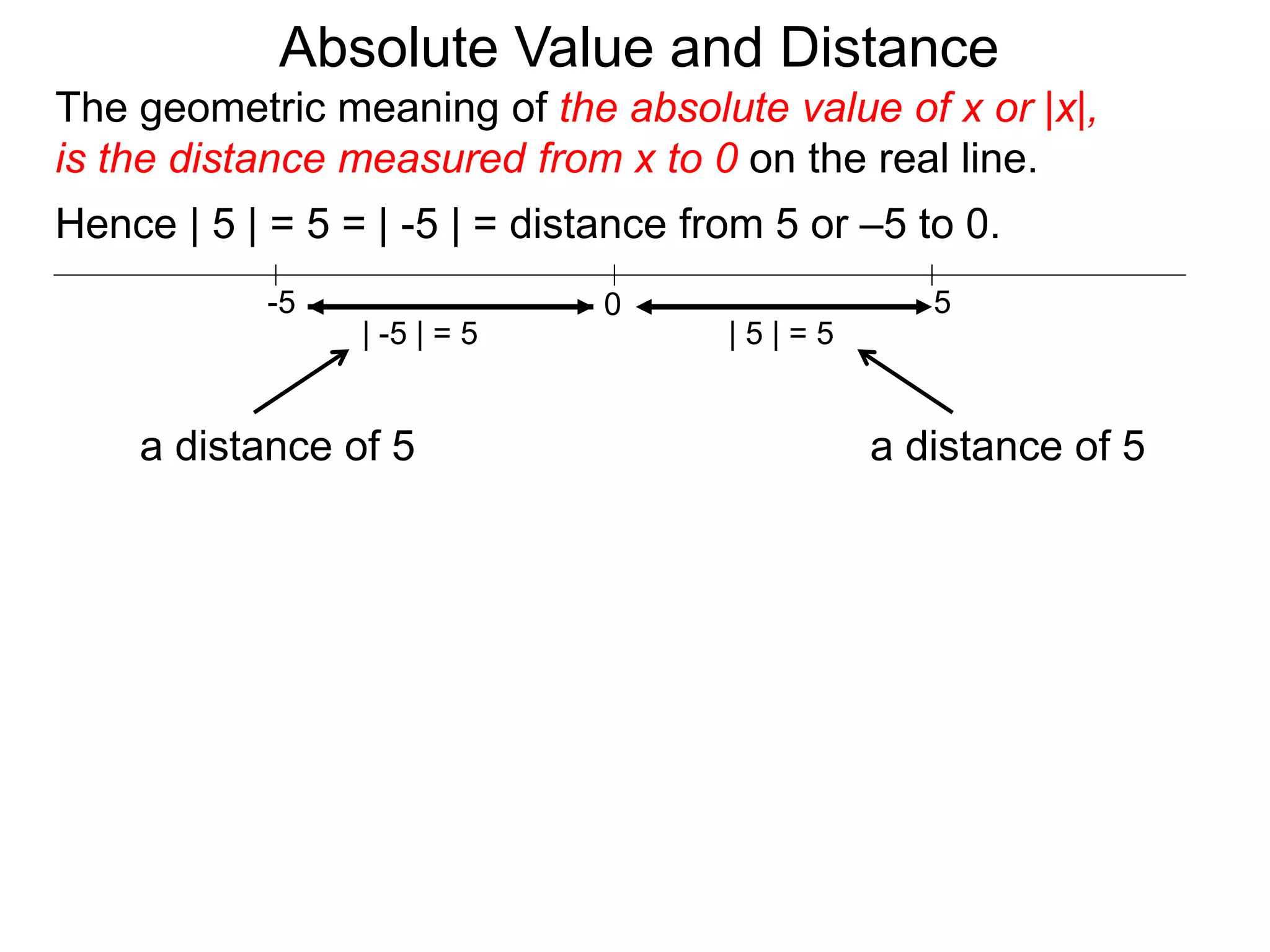
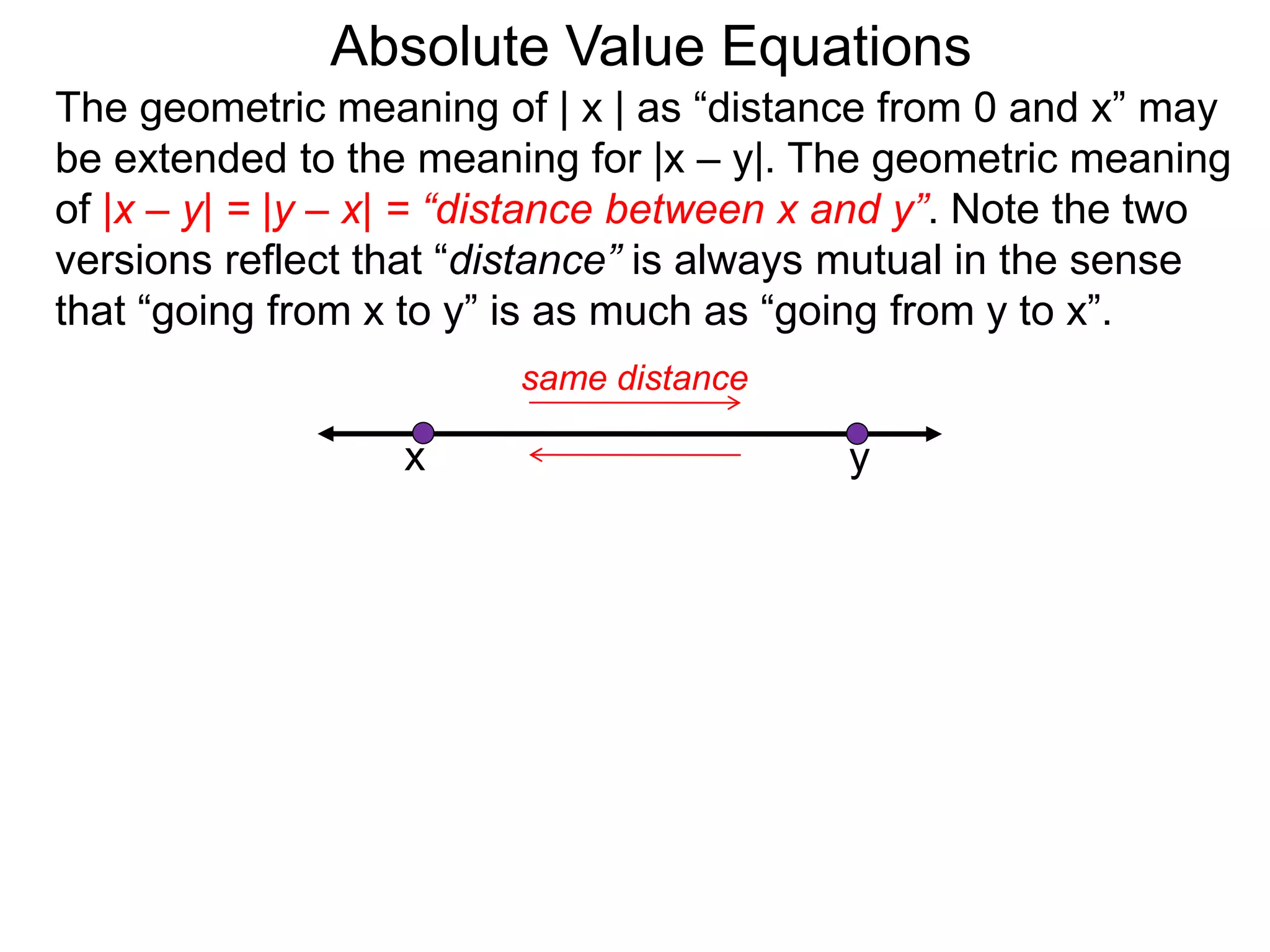
The document discusses absolute value and distance. It defines absolute value as the distance from a number to 0 on the number line. To calculate absolute value, if a number is positive or 0, its absolute value is itself, but if it is negative, its absolute value is its opposite. This makes absolute value always nonnegative, like a distance. The document provides examples of calculating absolute values and explains properties like absolute value is symmetric and follows the rule |xy| = |x| * |y|.

1. Absolute Value and Distance

2. To find the distance, a nonnegative number, between two points
L and R on a ruler, we subtract: R – L (i.e. Right Pt – Left Pt).
Absolute Value and Distance

3. L R
To find the distance, a nonnegative number, between two points
L and R on a ruler, we subtract: R – L (i.e. Right Pt – Left Pt).
Absolute Value and Distance

4. L R
Length from L to R is R – L
To find the distance, a nonnegative number, between two points
L and R on a ruler, we subtract: R – L (i.e. Right Pt – Left Pt).
Absolute Value and Distance

5. L R
Length from L to R is R – L
To find the distance, a nonnegative number, between two points
L and R on a ruler, we subtract: R – L (i.e. Right Pt – Left Pt).
Absolute Value and Distance

6. L R
Length from L to R is R – L
To find the distance, a nonnegative number, between two points
L and R on a ruler, we subtract: R – L (i.e. Right Pt – Left Pt).
Absolute Value and Distance
If we don’t know the values of x and y, then the distance is
either x – y or y – x.

7. L R
Length from L to R is R – L
To find the distance, a nonnegative number, between two points
L and R on a ruler, we subtract: R – L (i.e. Right Pt – Left Pt).
Absolute Value and Distance
If we don’t know the values of x and y, then the distance is
either x – y or y – x. For example, if x = 5 and y = 2,
then the distance between them is x – y = 3
where as y – x = –3 is negative.

8. L R
Length from L to R is R – L
To find the distance, a nonnegative number, between two points
L and R on a ruler, we subtract: R – L (i.e. Right Pt – Left Pt).
Absolute Value and Distance
If we don’t know the values of x and y, then the distance is
either x – y or y – x. For example, if x = 5 and y = 2,
then the distance between them is x – y = 3
where as y – x = –3 is negative. To clarify the two choices for
the distance, we put the absolute value symbol “l l” around the
expression as l x – y l, to remind us “to take the positive (or 0)
one” as the distance between x and y.

9. L R
Length from L to R is R – L
To find the distance, a nonnegative number, between two points
L and R on a ruler, we subtract: R – L (i.e. Right Pt – Left Pt).
Absolute Value and Distance
If we don’t know the values of x and y, then the distance is
either x – y or y – x. For example, if x = 5 and y = 2,
then the distance between them is x – y = 3
where as y – x = –3 is negative. To clarify the two choices for
the distance, we put the absolute value symbol “l l” around the
expression as l x – y l, to remind us “to take the positive (or 0)
one” as the distance between x and y. Facts about the “l l”:

10. L R
Length from L to R is R – L
To find the distance, a nonnegative number, between two points
L and R on a ruler, we subtract: R – L (i.e. Right Pt – Left Pt).
Absolute Value and Distance
If we don’t know the values of x and y, then the distance is
either x – y or y – x. For example, if x = 5 and y = 2,
then the distance between them is x – y = 3
where as y – x = –3 is negative. To clarify the two choices for
the distance, we put the absolute value symbol “l l” around the
expression as l x – y l, to remind us “to take the positive (or 0)
one” as the distance between x and y. Facts about the “l l”:
1. l # l ≥ 0 or “distance” is non–negative.

11. L R
Length from L to R is R – L
To find the distance, a nonnegative number, between two points
L and R on a ruler, we subtract: R – L (i.e. Right Pt – Left Pt).
Absolute Value and Distance
If we don’t know the values of x and y, then the distance is
either x – y or y – x. For example, if x = 5 and y = 2,
then the distance between them is x – y = 3
where as y – x = –3 is negative. To clarify the two choices for
the distance, we put the absolute value symbol “l l” around the
expression as l x – y l, to remind us “to take the positive (or 0)
one” as the distance between x and y. Facts about the “l l”:
1. l # l ≥ 0 or “distance” is non–negative.
2. l x – y l = l y – x l = the distance between x and y
so “distance” is symmetric (mutual).

12. L R
Length from L to R is R – L
To find the distance, a nonnegative number, between two points
L and R on a ruler, we subtract: R – L (i.e. Right Pt – Left Pt).
Absolute Value and Distance
If we don’t know the values of x and y, then the distance is
either x – y or y – x. For example, if x = 5 and y = 2,
then the distance between them is x – y = 3
where as y – x = –3 is negative. To clarify the two choices for
the distance, we put the absolute value symbol “l l” around the
expression as l x – y l, to remind us “to take the positive (or 0)
one” as the distance between x and y. Facts about the “l l”:
1. l # l ≥ 0 or “distance” is non–negative.
2. l x – y l = l y – x l = the distance between x and y
so “distance” is symmetric (mutual).
3. With y = 0, l x l = l –x l = the distance from x (or –x) to 0.

13. 0 5
Hence | 5 | = 5
| 5 | = 5
The geometric meaning of the absolute value of x or |x|,
is the distance measured from x to 0 on the real line.
a distance of 5
Absolute Value and Distance

14. 0 5-5
Hence | 5 | = 5 = | -5 |
| 5 | = 5
a distance of 5a distance of 5
The geometric meaning of the absolute value of x or |x|,
is the distance measured from x to 0 on the real line.
Absolute Value and Distance

15. 0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
a distance of 5a distance of 5
The geometric meaning of the absolute value of x or |x|,
is the distance measured from x to 0 on the real line.
Absolute Value and Distance

16. 0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
The geometric meaning of the absolute value of x or |x|,
is the distance measured from x to 0 on the real line.
Absolute Value and Distance

17. 0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
The geometric meaning of the absolute value of x or |x|,
is the distance measured from x to 0 on the real line.
Absolute Value and Distance

18. |x|=
x if x is positive or 0.
{
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
The geometric meaning of the absolute value of x or |x|,
is the distance measured from x to 0 on the real line.
Absolute Value and Distance

19. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
The geometric meaning of the absolute value of x or |x|,
is the distance measured from x to 0 on the real line.
Absolute Value and Distance

20. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | =
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
The geometric meaning of the absolute value of x or |x|,
is the distance measured from x to 0 on the real line.
Absolute Value and Distance

21. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | = –(–5)
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
Because –5 is negative,
use the 2nd part of the
rule and take its
opposite to obtain
its abs. value.
The geometric meaning of the absolute value of x or |x|,
is the distance measured from x to 0 on the real line.
Absolute Value and Distance

22. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | = –(–5) = 5.
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
Because –5 is negative,
use the 2nd part of the
rule and take its
opposite to obtain
its abs. value.
The geometric meaning of the absolute value of x or |x|,
is the distance measured from x to 0 on the real line.
Absolute Value and Distance

23. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | = –(–5) = 5.
Since the absolute value is never negative, an equation
such as |x14 – 3x9 + 1 | = –2 doesn't have any solution.
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
Because –5 is negative,
use the 2nd part of the
rule and take its
opposite to obtain
its abs. value.
The geometric meaning of the absolute value of x or |x|,
is the distance measured from x to 0 on the real line.
Absolute Value and Distance

24. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | = –(–5) = 5.
Since the absolute value is never negative, an equation
such as |x14 – 3x9 + 1 | = –2 doesn't have any solution.
Fact I. |x*y| = |x|*|y|.
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
Because –5 is negative,
use the 2nd part of the
rule and take its
opposite to obtain
its abs. value.
The geometric meaning of the absolute value of x or |x|,
is the distance measured from x to 0 on the real line.
Absolute Value and Distance

25. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | = –(–5) = 5.
Since the absolute value is never negative, an equation
such as |x14 – 3x9 + 1 | = –2 doesn't have any solution.
Fact I. |x*y| = |x|*|y|. For example, |–2*3 | = |–2|*|3| = 6.
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
Because –5 is negative,
use the 2nd part of the
rule and take its
opposite to obtain
its abs. value.
The geometric meaning of the absolute value of x or |x|,
is the distance measured from x to 0 on the real line.
Absolute Value and Distance

26. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | = –(–5) = 5.
Since the absolute value is never negative, an equation
such as |x14 – 3x9 + 1 | = –2 doesn't have any solution.
Fact I. |x*y| = |x|*|y|. For example, |–2*3 | = |–2|*|3| = 6.
Warning: In general |x ± y|  |x| ± |y|.
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
Because –5 is negative,
use the 2nd part of the
rule and take its
opposite to obtain
its abs. value.
The geometric meaning of the absolute value of x or |x|,
is the distance measured from x to 0 on the real line.
Absolute Value and Distance

27. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | = –(–5) = 5.
Since the absolute value is never negative, an equation
such as |x14 – 3x9 + 1 | = –2 doesn't have any solution.
Fact I. |x*y| = |x|*|y|. For example, |–2*3 | = |–2|*|3| = 6.
Warning: In general |x ± y|  |x| ± |y|.
For instance, |2 – 3 |  |2| – |3|  |2| + |3|.
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
Because –5 is negative,
use the 2nd part of the
rule and take its
opposite to obtain
its abs. value.
The geometric meaning of the absolute value of x or |x|,
is the distance measured from x to 0 on the real line.
Absolute Value and Distance

28. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | = –(–5) = 5.
Since the absolute value is never negative, an equation
such as |x14 – 3x9 + 1 | = –2 doesn't have any solution.
Fact I. |x*y| = |x|*|y|. For example, |–2*3 | = |–2|*|3| = 6.
Warning: In general |x ± y|  |x| ± |y|.
For instance, |2 – 3 |  |2| – |3|  |2| + |3|.
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
A “| |” can not be split
into two | |’s when
adding or subtracting.
Because –5 is negative,
use the 2nd part of the
rule and take its
opposite to obtain
its abs. value.
The geometric meaning of the absolute value of x or |x|,
is the distance measured from x to 0 on the real line.
Absolute Value and Distance

29. Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations.
Absolute Value Equations

30. Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
Absolute Value Equations

31. Fact II: If |#| = a, a >0, (where # is any expression)
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
Absolute Value Equations

32. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Absolute Value Equations

33. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Absolute Value Equations

34. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3 then x = –3 or x = 3
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Absolute Value Equations

35. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3 then x = –3 or x = 3
In picture, if | x | = 3 then
0 x = 3x = –3
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Absolute Value Equations

36. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3 then x = –3 or x = 3
b. | –2x | = 5
In picture, if | x | = 3 then
0 x = 3x = –3
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Absolute Value Equations

37. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3 then x = –3 or x = 3
b. | –2x | = 5
In picture, if | x | = 3 then
0 x = 3x = –3
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Drop the “| |” and set the formula to 5 and –5.
Absolute Value Equations

38. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3 then x = –3 or x = 3
b. | –2x | = 5
–2x = –5 or –2x = 5
In picture, if | x | = 3 then
0 x = 3x = –3
Drop the “| |” and set the formula to 5 and –5.
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Absolute Value Equations

39. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3 then x = –3 or x = 3
b. | –2x | = 5
–2x = –5 or –2x = 5
x = 5/2
In picture, if | x | = 3 then
0 x = 3x = –3
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Drop the “| |” and set the formula to 5 and –5.
Absolute Value Equations

40. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3 then x = –3 or x = 3
b. | –2x | = 5
–2x = –5 or –2x = 5
x = –5/2x = 5/2
In picture, if | x | = 3 then
0 x = 3x = –3
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Drop the “| |” and set the formula to 5 and –5.
Absolute Value Equations

41. c. | 2x – 3 | = 5
Absolute Value Equations

42. c. | 2x – 3 | = 5
Drop the “| |”.
Absolute Value Equations

43. c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
Drop the “| |”.
Absolute Value Equations

44. c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = –2
Drop the “| |”.
Absolute Value Equations

45. c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = –2
x = –1
Drop the “| |”.
Absolute Value Equations

46. c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 82x = –2
x = –1
Drop the “| |”.
Absolute Value Equations

47. c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”.
Absolute Value Equations

48. d. | 2 – 3x | + 2 = 4
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”.
Absolute Value Equations

49. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”.
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations

50. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
| 2 – 3x | + 2 = 4
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”.
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations

51. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
| 2 – 3x | + 2 = 4
| 2 – 3x | = 2
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”.
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations

52. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
| 2 – 3x | + 2 = 4
| 2 – 3x | = 2
Drop the | |.
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”.
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations

53. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
| 2 – 3x | + 2 = 4
| 2 – 3x | = 2
Drop the | |.
2 – 3x = 22 – 3x = –2 or
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”.
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations

54. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
| 2 – 3x | + 2 = 4
| 2 – 3x | = 2
Drop the | |.
2 – 3x = 22 – 3x = –2
–3x = –4
or
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”.
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations

55. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
| 2 – 3x | + 2 = 4
| 2 – 3x | = 2
Drop the | |.
2 – 3x = 22 – 3x = –2
–3x = –4
or
x = 4/3
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”.
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations

56. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
| 2 – 3x | + 2 = 4
| 2 – 3x | = 2
Drop the | |.
2 – 3x = 22 – 3x = –2
–3x = 0–3x = –4
or
x = 4/3
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”.
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations

57. Absolute Value Equations
d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
| 2 – 3x | + 2 = 4
| 2 – 3x | = 2
Drop the | |.
2 – 3x = 22 – 3x = –2
–3x = 0
x = 0
–3x = –4
or
x = 4/3
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”.
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4

58. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|.
Absolute Value Equations

59. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”.
Absolute Value Equations

60. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations

61. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
yx
same distance

62. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
|9 – 3| = 6 = |3 – 9|
yx
same distance

63. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
|9 – 3| = 6 = |3 – 9| and |(–8) – (–1)| = 7.
yx
same distance

64. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
|9 – 3| = 6 = |3 – 9| and |(–8) – (–1)| = 7.
We can solve for x using this method.
yx
same distance

65. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
|9 – 3| = 6 = |3 – 9| and |(–8) – (–1)| = 7.
We can solve for x using this method.
yx
same distance
Example B. Solve for x geometrically if |x – 7| = 12.

66. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
|9 – 3| = 6 = |3 – 9| and |(–8) – (–1)| = 7.
We can solve for x using this method.
yx
same distance
Example B. Solve for x geometrically if |x – 7| = 12.
We want the locations of x's that are 12 units away from 7.

67. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
|9 – 3| = 6 = |3 – 9| and |(–8) – (–1)| = 7.
We can solve for x using this method.
yx
same distance
Example B. Solve for x geometrically if |x – 7| = 12.
We want the locations of x's that are 12 units away from 7.
7
1212
x x

68. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
|9 – 3| = 6 = |3 – 9| and |(–8) – (–1)| = 7.
We can solve for x using this method.
yx
same distance
Example B. Solve for x geometrically if |x – 7| = 12.
We want the locations of x's that are 12 units away from 7.
7
1212
x x
We see that x = –5 or x = 19.

69. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
|9 – 3| = 6 = |3 – 9| and |(–8) – (–1)| = 7.
We can solve for x using this method.
yx
same distance
Example B. Solve for x geometrically if |x – 7| = 12.
We want the locations of x's that are 12 units away from 7.
7
1212
x x
(Solve it algebraically and verify these are the answers.)
We see that x = –5 or x = 19.

70. Absolute Value Equations
c
r
x = c + r
Recall |x*y| = |x|*|y|, so we can pull out constant multiple
hence |3x| = 3|x| and |3x – 6| = |3(x – 2)| = 3|(x – 2)|.
In general, the abs–equation means to find x where
|x – c| = r ( ≥ 0)
distance between x and c is r.
in picture:
r
x = c – r
Hence the solutions for |x – 3 | = 2
are x = 3 – 2 =1 and x = 3 + 2 = 5.
Example C. Solve for x geometrically if |–3x + 6| = 4. Draw.
Since |–3x – 6| = |–3(x + 2)| = 3|x + 2| so
3|x + 2| = 4 or that |x – (–2)| = 4/3.
Hence x = (–2) ± 4/3
or x = –2/3 and x = –3 1
3
–2 x = –2/3x = –3
4/34/3
1
3
|x – (–2)| = 4/3

71. Ex. A.
1. Is it always true that I+x| = x? Give reason for your answer.
2. Is it always true that |–x| = x? Give reason for your answer.
Absolute Value Equations
Ex. B. Drop the | | and write the problem into two equations
then solve for x (if any) and label the answer(s) on the real
line.
3. |x| = 2 4. |x| = 5 5. |–x| = 2 6. |–x| = 5
7. |x| = –2 8. |–2x| = 6 9. |–3x| = 6 10. |–x| = –5
11. |3 – x| = –5 12. |3 + x| = 7 13. |x – 9| = 5
14. |5 – x| = 5 15. |4 + x| = 9 16. |2x + 1| = 3
17. |4 – 5x| = 3 18. |3 + 2x| = 7 19. |–2x + 3| = 5
20. |4 – 5x| = –3 21. |2x + 1| – 1= 5 22. 3|2x + 1| – 1= 5

72. Absolute Value Equations
Ex. C. Solve for x by using the geometric method.
31. |7x – 2| = 1
23. |3 – x| = 5 24. |x – 5| = 5 25. |7 – x| = 3
26. |8 + x| = 9 27. |x + 1| = 3 28. |2x + 1| = 3
30. |3 + 2x| = 729. |–2x + 3| = 2