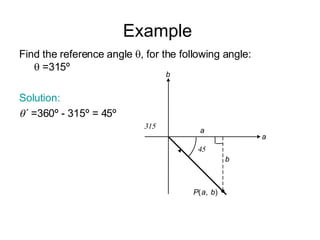
The document defines trigonometric functions for any angle using ratios based on the coordinates of a point on the terminal side of the angle. It introduces the concept of a reference angle, which is the acute angle formed by the terminal side and the x-axis, and explains how to use reference angles to evaluate trigonometric functions for non-acute angles by determining the sign from the quadrant. An example problem demonstrates evaluating trig functions using a reference angle.

1. Trigonometric Functions of Any Angle

3. Text Example Let P = (-3, -4) be a point on the terminal side of  . Find each of the six trigonometric functions of  . Solution The situation is shown below. We need values for x , y , and r to evaluate all six trigonometric functions. We are given the values of x and y . Because P = (-3, -4) is a point on the terminal side of  , x = -3 and y = -4. Furthermore, r x = -3 y = -4 P = (-3, -4)  x y -5 5 -5 5

5. The Signs of the Trigonometric Functions x y Quadrant II Sine and cosecant positive (-,+) Quadrant I All functions positive (+,+) Quadrant III tangent and cotangent positive (-,-) Quadrant IV cosine and secant positive (+,-)

6. Example: Evaluating Trigonometric Functions Given tan  = -2 / 3 and cos  > 0, find cos  and csc  . Solution Because the tangent is negative and the cosine is positive,  lies in quadrant IV. This will help us to determine whether the negative sign in tan  = -2 / 3 should be associated with the numerator or the denominator. Keep in mind that in quadrant IV, x is positive and y is negative. Thus, In quadrant IV, y is negative. x = 3 y = -2 P = (3, -2)  x y -5 5 -5 5 r = 13 Thus, x = 3 and y = -2. Furthermore, Now that we know x , y and r , find cos  and csc  .

11. Example: Using Reference Angles to Evaluate Trigonometric Functions Use reference angles to find the exact value of each of the following trigonometric functions. a. sin 135° x y 135° 45° more more x y 4  / 3  / 3 x y  / 3 -  / 3