Uploaded byTzenma
PPTX, PDF178 views

7 system of linear equations ii x

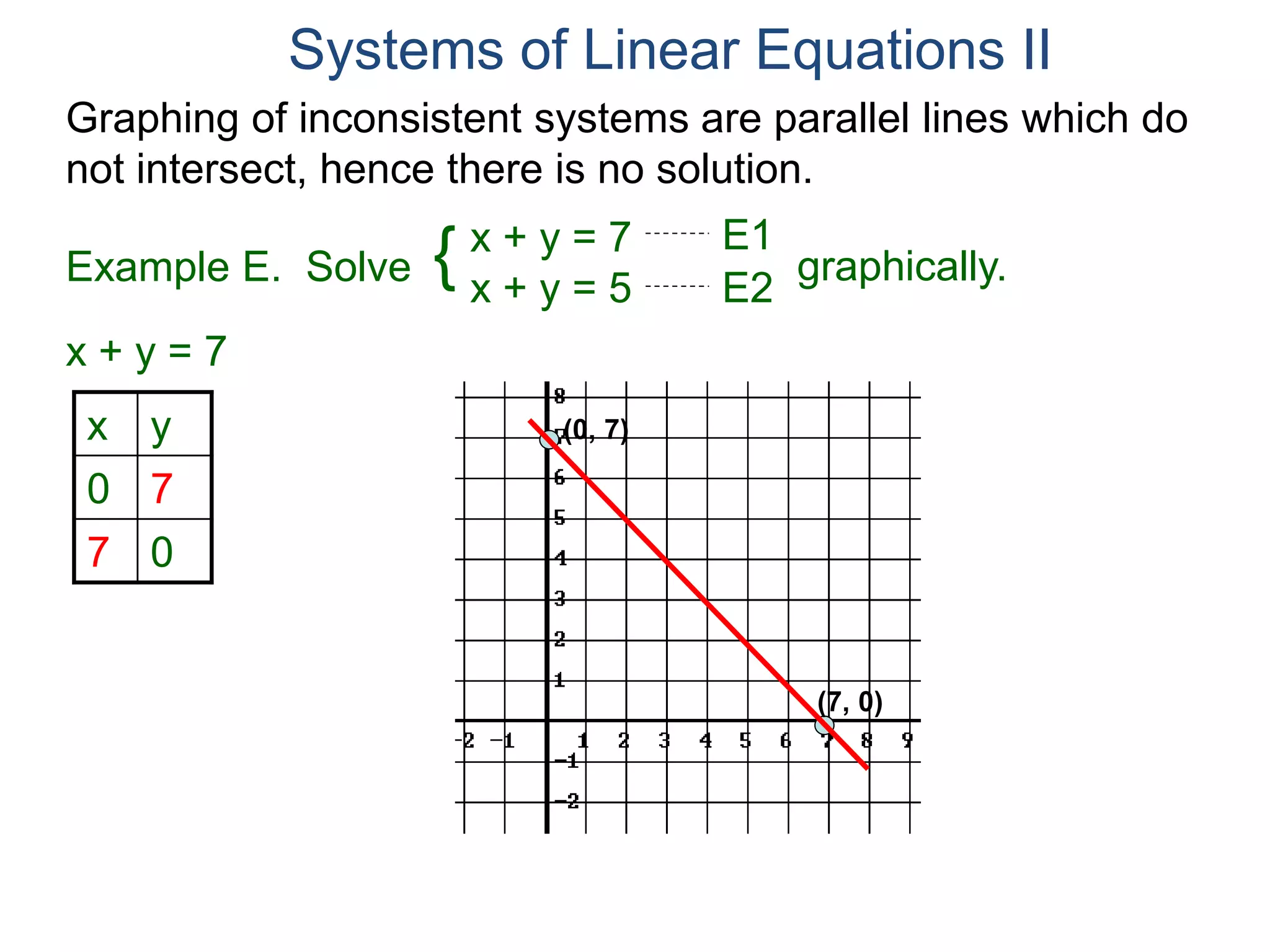
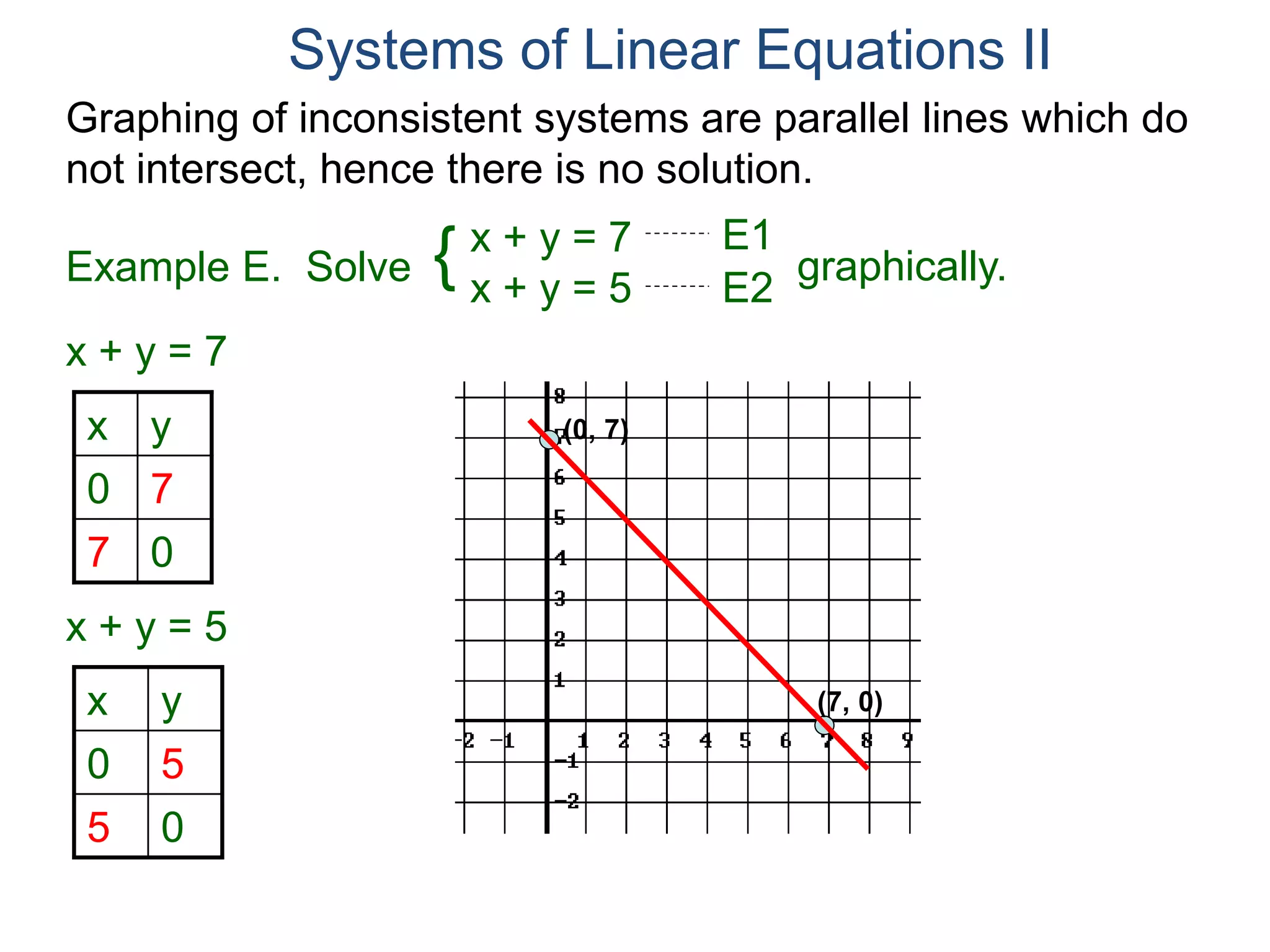
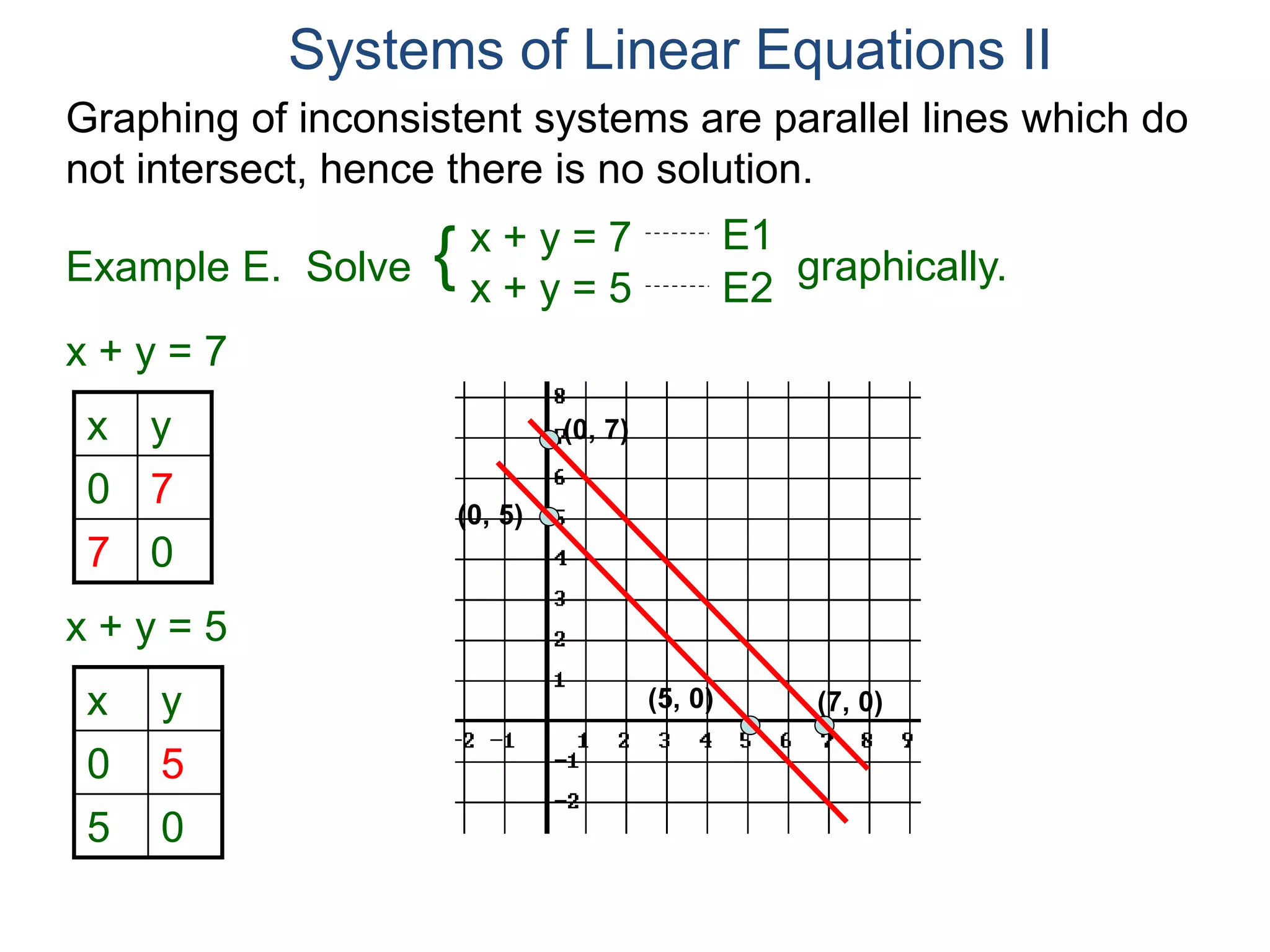
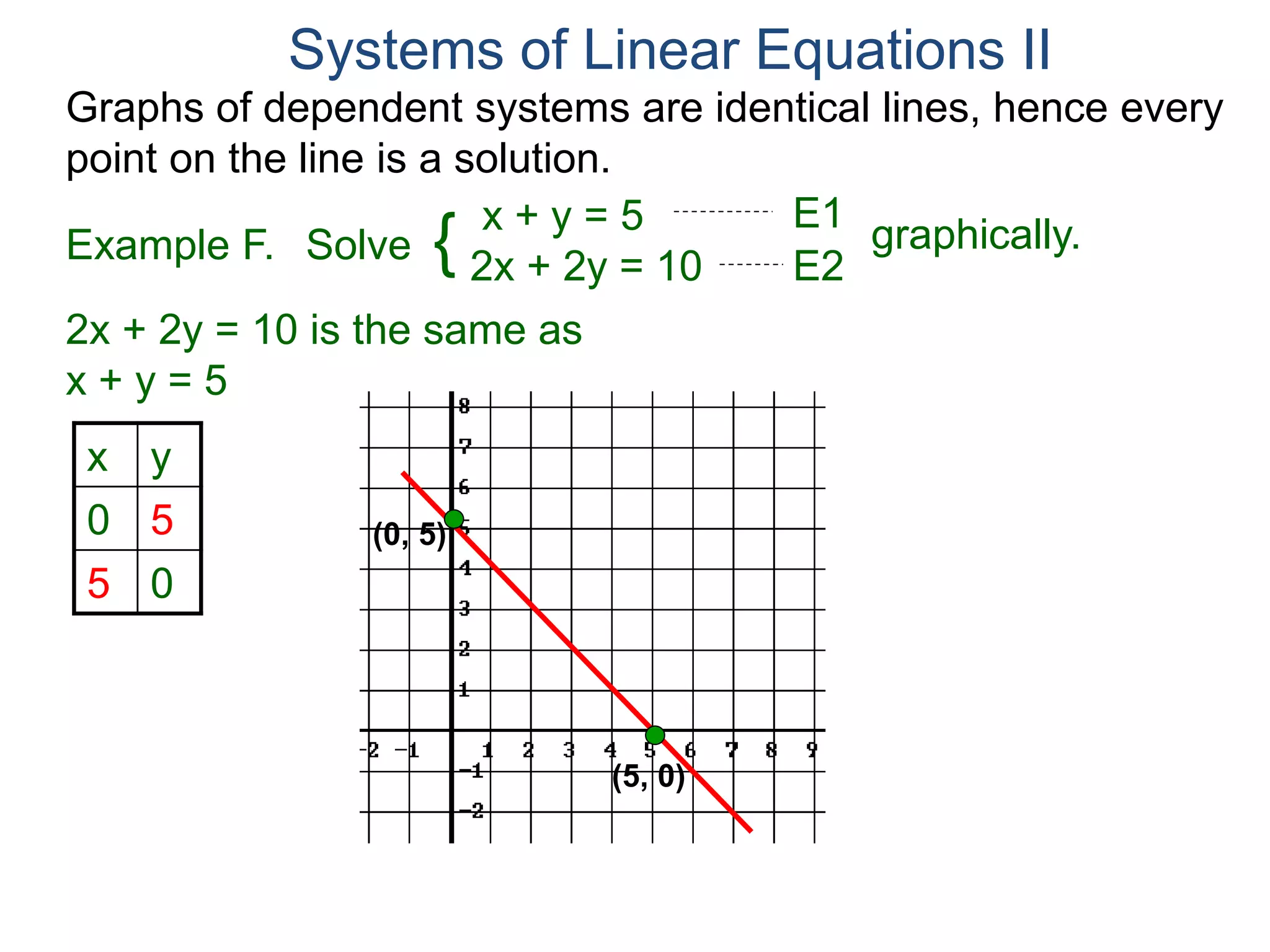
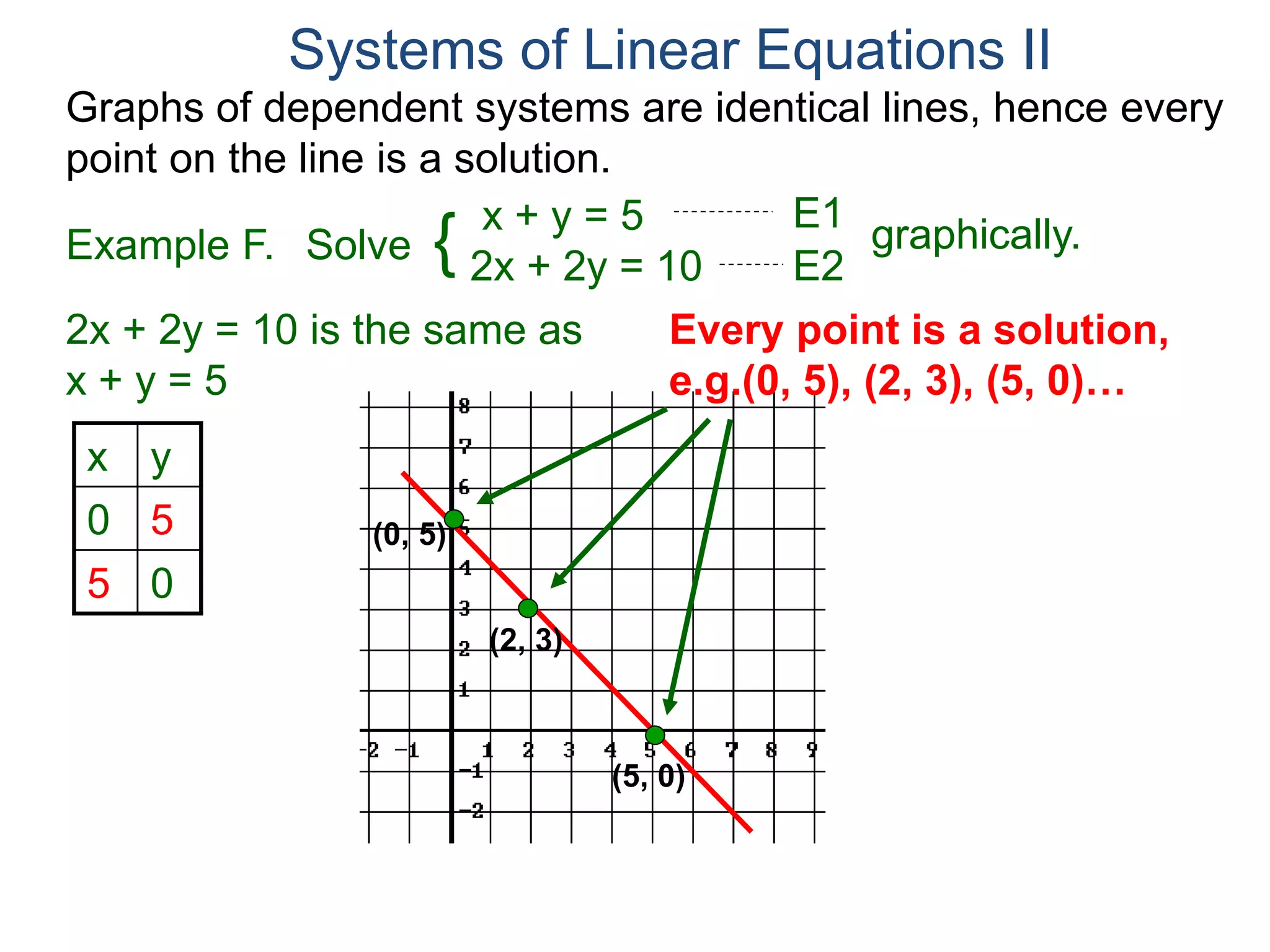
The document provides an example of solving a system of linear equations using the substitution method. It begins with the system 2x + y = 7 and x + y = 5. It solves the second equation for x in terms of y, getting x = 5 - y. This expression for x is then substituted into the first equation, giving 10 - 2y + y = 7, which can be solved to find the value of y, and then substituted back into the original equation to find the value of x. The solution is presented as (2, 3). The document then provides two additional examples demonstrating how to set up and solve systems of equations using the substitution method.

Embed presentation

Download to read offline
Systems of Linear Equations II
Systems of Linear Equations II Example A. At Pizza Grande, one coupon C may be exchanged for three slices of pizza (P) and five donuts (D). We have 5 slices of pizzas, 3 donuts and 2 coupons. What do we have after exchanging the 2 coupons?
Systems of Linear Equations II Example A. At Pizza Grande, one coupon C may be exchanged for three slices of pizza (P) and five donuts (D). We have 5 slices of pizzas, 3 donuts and 2 coupons. What do we have after exchanging the 2 coupons? The coupon value of C may be recorded as C = 5P + 3D.
Systems of Linear Equations II Example A. At Pizza Grande, one coupon C may be exchanged for three slices of pizza (P) and five donuts (D). We have 5 slices of pizzas, 3 donuts and 2 coupons. What do we have after exchanging the 2 coupons? The coupon value of C may be recorded as C = 5P + 3D. 5 slices of pizzas, 3 donuts and 2 coupons is 5P + 3D+ 2C.
Systems of Linear Equations II Example A. At Pizza Grande, one coupon C may be exchanged for three slices of pizza (P) and five donuts (D). We have 5 slices of pizzas, 3 donuts and 2 coupons. What do we have after exchanging the 2 coupons? The coupon value of C may be recorded as C = 5P + 3D. 5 slices of pizzas, 3 donuts and 2 coupons is 5P + 3D+ 2C. Exchanging the 2 coupons for pizzas and donuts, we would have 5P + 3D + 2C
Systems of Linear Equations II Example A. At Pizza Grande, one coupon C may be exchanged for three slices of pizza (P) and five donuts (D). We have 5 slices of pizzas, 3 donuts and 2 coupons. What do we have after exchanging the 2 coupons? The coupon value of C may be recorded as C = 5P + 3D. 5 slices of pizzas, 3 donuts and 2 coupons is 5P + 3D+ 2C. Exchanging the 2 coupons for pizzas and donuts, we would have 5P + 3D + 2C = 5P + 3D + 2(5P + 3D)
Systems of Linear Equations II Example A. At Pizza Grande, one coupon C may be exchanged for three slices of pizza (P) and five donuts (D). We have 5 slices of pizzas, 3 donuts and 2 coupons. What do we have after exchanging the 2 coupons? The coupon value of C may be recorded as C = 5P + 3D. 5 slices of pizzas, 3 donuts and 2 coupons is 5P + 3D+ 2C. Exchanging the 2 coupons for pizzas and donuts, we would have 5P + 3D + 2C = 5P + 3D + 2(5P + 3D) = 5P + 3D + 10P + 6D
Systems of Linear Equations II Example A. At Pizza Grande, one coupon C may be exchanged for three slices of pizza (P) and five donuts (D). We have 5 slices of pizzas, 3 donuts and 2 coupons. What do we have after exchanging the 2 coupons? The coupon value of C may be recorded as C = 5P + 3D. 5 slices of pizzas, 3 donuts and 2 coupons is 5P + 3D+ 2C. Exchanging the 2 coupons for pizzas and donuts, we would have 5P + 3D + 2C = 5P + 3D + 2(5P + 3D) = 5P + 3D + 10P + 6D = 15P + 9D or 15 slices of pizzas and 9 donuts.
In math, the phrase "substitute (the expression) back into ...“ means to do the exchange, using the given coupon–expression, in the targeted equations, or expressions mentioned. Systems of Linear Equations II Example A. At Pizza Grande, one coupon C may be exchanged for three slices of pizza (P) and five donuts (D). We have 5 slices of pizzas, 3 donuts and 2 coupons. What do we have after exchanging the 2 coupons? The coupon value of C may be recorded as C = 5P + 3D. 5 slices of pizzas, 3 donuts and 2 coupons is 5P + 3D+ 2C. Exchanging the 2 coupons for pizzas and donuts, we would have 5P + 3D + 2C = 5P + 3D + 2(5P + 3D) = 5P + 3D + 10P + 6D = 15P + 9D or 15 slices of pizzas and 9 donuts.
There are two other methods to solve system of equations. Systems of Linear Equations II
There are two other methods to solve system of equations. Substitution Method Systems of Linear Equations II
There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation. Systems of Linear Equations II
2x + y = 7 E1 x + y = 5 E2 Solve by the substitution method. Systems of Linear Equations II Example B. { There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation.
2x + y = 7 E1 x + y = 5 E2 Solve by the substitution method. From E2, x + y = 5, we get x = 5 – y. Systems of Linear Equations II Example B. { There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation.
2x + y = 7 E1 x + y = 5 E2 Solve by the substitution method. From E2, x + y = 5, we get x = 5 – y. Systems of Linear Equations II Example B. { There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation. This is the coupon expression so we may exchange x = 5 – y
2x + y = 7 E1 x + y = 5 E2 Solve by the substitution method. From E2, x + y = 5, we get x = 5 – y. Then we replace x by (5 – y) in E1 and get 2(5 – y) + y = 7 Systems of Linear Equations II Example B. { There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation. This is the coupon expression so we may exchange x = 5 – y
2x + y = 7 E1 x + y = 5 E2 Solve by the substitution method. From E2, x + y = 5, we get x = 5 – y. Then we replace x by (5 – y) in E1 and get 2(5 – y) + y = 7 10 – 2y + y = 7 Systems of Linear Equations II Example B. { There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation. This is the coupon expression so we may exchange x = 5 – y
2x + y = 7 E1 x + y = 5 E2 Solve by the substitution method. From E2, x + y = 5, we get x = 5 – y. Then we replace x by (5 – y) in E1 and get 2(5 – y) + y = 7 10 – 2y + y = 7 10 – y = 7  3 = y Systems of Linear Equations II Example B. { There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation. This is the coupon expression so we may exchange x = 5 – y
2x + y = 7 E1 x + y = 5 E2 Solve by the substitution method. From E2, x + y = 5, we get x = 5 – y. Then we replace x by (5 – y) in E1 and get 2(5 – y) + y = 7 10 – 2y + y = 7 10 – y = 7  3 = y Systems of Linear Equations II Example B. { Put 3 = y back to E2 to find x, we get x + 3 = 5 There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation. This is the coupon expression so we may exchange x = 5 – y
2x + y = 7 E1 x + y = 5 E2 Solve by the substitution method. From E2, x + y = 5, we get x = 5 – y. Then we replace x by (5 – y) in E1 and get 2(5 – y) + y = 7 10 – 2y + y = 7 10 – y = 7  3 = y Systems of Linear Equations II Example B. { Put 3 = y back to E2 to find x, we get x + 3 = 5  x = 2 Therefore the solution is (2, 3) There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation. This is the coupon expression so we may exchange x = 5 – y
We use the substitution method when it's easy to solve for one of the variable in terms of the other. Systems of Linear Equations II
We use the substitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. Systems of Linear Equations II
We use the substitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. Systems of Linear Equations II Example C. {
We use the substitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. By inspection, we see that it's easy to solve for the y using E1. Systems of Linear Equations II Example C. {
We use the substitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. By inspection, we see that it's easy to solve for the y using E1. From E1, 2x – y = 7, we get 2x – 7= y. Systems of Linear Equations II Example C. {
We use the substitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. By inspection, we see that it's easy to solve for the y using E1. From E1, 2x – y = 7, we get 2x – 7= y. Substitute y by (2x – 7) in E2 and get 3x + 2(2x – 7) = 7 Systems of Linear Equations II Example C. {
We use the substitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. By inspection, we see that it's easy to solve for the y using E1. From E1, 2x – y = 7, we get 2x – 7= y. Substitute y by (2x – 7) in E2 and get 3x + 2(2x – 7) = 7 3x + 4x – 14 = 7 Systems of Linear Equations II Example C. {
We use the substitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. By inspection, we see that it's easy to solve for the y using E1. From E1, 2x – y = 7, we get 2x – 7= y. Substitute y by (2x – 7) in E2 and get 3x + 2(2x – 7) = 7 3x + 4x – 14 = 7 7x = 21 x = 3 Systems of Linear Equations II Example C. {
We use the substitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. By inspection, we see that it's easy to solve for the y using E1. From E1, 2x – y = 7, we get 2x – 7= y. Substitute y by (2x – 7) in E2 and get 3x + 2(2x – 7) = 7 3x + 4x – 14 = 7 7x = 21 x = 3 Systems of Linear Equations II Example C. { To find y, use the substitution equation, set x = 3 in y = 2x – 7
We use the substitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. By inspection, we see that it's easy to solve for the y using E1. From E1, 2x – y = 7, we get 2x – 7= y. Substitute y by (2x – 7) in E2 and get 3x + 2(2x – 7) = 7 3x + 4x – 14 = 7 7x = 21 x = 3 Systems of Linear Equations II Example C. { To find y, use the substitution equation, set x = 3 in y = 2x – 7 y = 2(3) – 7 y = -1
We use the substitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. By inspection, we see that it's easy to solve for the y using E1. From E1, 2x – y = 7, we get 2x – 7= y. Substitute y by (2x – 7) in E2 and get 3x + 2(2x – 7) = 7 3x + 4x – 14 = 7 7x = 21 x = 3 Systems of Linear Equations II Example C. { To find y, use the substitution equation, set x = 3 in y = 2x – 7 y = 2(3) – 7 y = -1 Hence the solution is (3, -1).
Graphing Method Systems of Linear Equations II
Graphing Method Given a system of linear equations the graph of each equation is a straight line. Systems of Linear Equations II
Graphing Method Given a system of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Systems of Linear Equations II
Graphing Method Given a system of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. Systems of Linear Equations II
Graphing Method Given a system of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II
Graphing Method Given a system of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D.
Graphing Method Given a system of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method.
Graphing Method Given a system of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x y 0 0 2x + y = 7
Graphing Method Given a system of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x y 0 7 0 2x + y = 7
Graphing Method Given a system of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x y 0 7 7/2 0 2x + y = 7 E2
Graphing Method Given a system of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x y 0 7 7/2 0 2x + y = 7 E2 (Check another point.)
Graphing Method Given a system of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x y 0 7 7/2 0 2x + y = 7 E1 E2 (0, 7) (7/2, 0) E1(Check another point.)
Graphing Method Given a system of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x + y = 5 x y 0 7 7/2 0 2x + y = 7 x y 0 0 (0, 7) (7/2, 0) E1(Check another point.)
Graphing Method Given a system of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x y 0 7 7/2 0 2x + y = 7 x + y = 5 x y 0 5 5 0 (0, 7) (7/2, 0) E1(Check another point.)
Graphing Method Given a system of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x y 0 7 7/2 0 2x + y = 7 (0, 7) (7/2, 0) (0, 5) (5, 0) E2 x + y = 5 x y 0 5 5 0 E1(Check another point.)
Graphing Method Given a system of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x y 0 7 7/2 0 2x + y = 7 (0, 7) (7/2, 0) (0, 5) (5, 0) The intersection (2, 3) is the solution E1 E2 x + y = 5 x y 0 5 5 0 E1(Check another point.)
Graphing of inconsistent systems are parallel lines which do not intersect, hence there is no solution. Systems of Linear Equations II
Graphing of inconsistent systems are parallel lines which do not intersect, hence there is no solution. Systems of Linear Equations II x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example E.
Graphing of inconsistent systems are parallel lines which do not intersect, hence there is no solution. x + y = 7 x y 0 7 7 0 Systems of Linear Equations II x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example E.
Graphing of inconsistent systems are parallel lines which do not intersect, hence there is no solution. x + y = 7 x y 0 7 7 0 (0, 7) (7, 0) Systems of Linear Equations II x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example E.
Graphing of inconsistent systems are parallel lines which do not intersect, hence there is no solution. x + y = 7 x y 0 7 7 0 x y 0 5 5 0 (0, 7) (7, 0) Systems of Linear Equations II x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example E. x + y = 5
Graphing of inconsistent systems are parallel lines which do not intersect, hence there is no solution. x + y = 7 x y 0 7 7 0 x y 0 5 5 0 (0, 7) (7, 0) (0, 5) (5, 0) Systems of Linear Equations II x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example E. x + y = 5
Graphing of inconsistent systems are parallel lines which do not intersect, hence there is no solution. x + y = 7 x y 0 7 7 0 x y 0 5 5 0 (0, 7) (7, 0) (0, 5) (5, 0) No intersection. No solution Systems of Linear Equations II x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example E. x + y = 5
Graphs of dependent systems are identical lines, hence every point on the line is a solution. Systems of Linear Equations II
Graphs of dependent systems are identical lines, hence every point on the line is a solution. Systems of Linear Equations II x + y = 5 2x + 2y = 10 Solve graphically.{ E1 E2Example F.
Graphs of dependent systems are identical lines, hence every point on the line is a solution. 2x + 2y = 10 is the same as x + y = 5 Systems of Linear Equations II x + y = 5 2x + 2y = 10 Solve graphically.{ E1 E2Example F.
Graphs of dependent systems are identical lines, hence every point on the line is a solution. 2x + 2y = 10 is the same as x + y = 5 x y 0 5 5 0 Systems of Linear Equations II x + y = 5 2x + 2y = 10 Solve graphically.{ E1 E2Example F.
Graphs of dependent systems are identical lines, hence every point on the line is a solution. 2x + 2y = 10 is the same as x + y = 5 x y 0 5 5 0 (5, 0) (0, 5) Systems of Linear Equations II x + y = 5 2x + 2y = 10 Solve graphically.{ E1 E2Example F.
Graphs of dependent systems are identical lines, hence every point on the line is a solution. 2x + 2y = 10 is the same as x + y = 5 x y 0 5 5 0 (5, 0) (0, 5) Every point is a solution, e.g.(0, 5), (2, 3), (5, 0)… (2, 3) Systems of Linear Equations II x + y = 5 2x + 2y = 10 Solve graphically.{ E1 E2Example F.
Systems of Linear Equations II 4. {–x + 2y = –12 y = 4 – 2x Exercise. Solve by the substitution method. 1. {y = 3 – x 2x + y = 4 2. 3. {x = 3 – y 2x – y = 6 {x + y = 3 2x + 6 = y 5. {3x + 4y = 3 x = 6 + 2y 6. { x = 3 – 3y 2x – 9y = –4 10. Graph the inconsistent system { x + 3y = 4 2x + 6y = 8 {2x – y = 2 8x – 4y = 6 Problem 7, 8, 9: Solve problem 1, 2, and 3 by graphing. 11. Graph the dependent system

More Related Content

PPTX
Calculus Assignment Help
byMaths Assignment Help
 
PPTX
Constant-Coefficient Linear Differential Equations
byashikul akash
 
PPTX
4.6 radical equations
bymath123b
 
PDF
Differential Equation
byV.M. Raut Shri Shivaji Science College, Amravati
 
PPTX
2 2 addition and subtraction ii
bymath123b
 
PDF
Improper integral
byV.M. Raut Shri Shivaji Science College, Amravati
 
PPTX
Calculus Homework Help
byMath Homework Solver
 
PPTX
Solving systems of equations
bybillingssr
 
Calculus Assignment Help
byMaths Assignment Help
 
Constant-Coefficient Linear Differential Equations
byashikul akash
 
4.6 radical equations
bymath123b
 
Differential Equation
byV.M. Raut Shri Shivaji Science College, Amravati
 
2 2 addition and subtraction ii
bymath123b
 
Improper integral
byV.M. Raut Shri Shivaji Science College, Amravati
 
Calculus Homework Help
byMath Homework Solver
 
Solving systems of equations
bybillingssr
 

What's hot

PPT
6.2 presentation
byRandall Micallef
 
DOCX
Liner Differential Equation
byV.M. Raut Shri Shivaji Science College, Amravati
 
PPTX
Calculus Homework Help
byMath Homework Solver
 
PDF
Ncert solutions for class 7 maths chapter 1 integers exercise 1.2
byjobazine India
 
PDF
E content on algebra & trignomentry
byV.M. Raut Shri Shivaji Science College, Amravati
 
PPT
Systems of equations by graphing by graphing sect 6 1
bytty16922
 
PPTX
Differential equations
bySanthanam Krishnan
 
PPTX
Simultaneous equations
byfisayo omoniyi
 
PDF
Succesive differntiation
byJaydevVadachhak
 
PPTX
43literal equations
byalg1testreview
 
PPTX
2 7 variations
bymath123b
 
DOCX
.Chapter7&8.
byjennytuazon01630
 
PPTX
formulation of first order linear and nonlinear 2nd order differential equation
byMahaswari Jogia
 
PPTX
5 1 complex numbers-x
bymath123b
 
PDF
Basic math solution
byBijayKanojiya
 
PDF
Solutions Manual for An Introduction To Abstract Algebra With Notes To The Fu...
byAladdinew
 
PPT
Solving linear systems by the substitution method
bybutterflyrose0411
 
PDF
Chapter0
byosamahussien
 
PDF
Mcq differential and ordinary differential equation
bySayyad Shafi
 
PDF
Multiple Choice Questions_Successive Differentiation (CALCULUS)
bysanjay gupta
 
6.2 presentation
byRandall Micallef
 
Liner Differential Equation
byV.M. Raut Shri Shivaji Science College, Amravati
 
Calculus Homework Help
byMath Homework Solver
 
Ncert solutions for class 7 maths chapter 1 integers exercise 1.2
byjobazine India
 
E content on algebra & trignomentry
byV.M. Raut Shri Shivaji Science College, Amravati
 
Systems of equations by graphing by graphing sect 6 1
bytty16922
 
Differential equations
bySanthanam Krishnan
 
Simultaneous equations
byfisayo omoniyi
 
Succesive differntiation
byJaydevVadachhak
 
43literal equations
byalg1testreview
 
2 7 variations
bymath123b
 
.Chapter7&8.
byjennytuazon01630
 
formulation of first order linear and nonlinear 2nd order differential equation
byMahaswari Jogia
 
5 1 complex numbers-x
bymath123b
 
Basic math solution
byBijayKanojiya
 
Solutions Manual for An Introduction To Abstract Algebra With Notes To The Fu...
byAladdinew
 
Solving linear systems by the substitution method
bybutterflyrose0411
 
Chapter0
byosamahussien
 
Mcq differential and ordinary differential equation
bySayyad Shafi
 
Multiple Choice Questions_Successive Differentiation (CALCULUS)
bysanjay gupta
 

Similar to 7 system of linear equations ii x

PPTX
3 4 systems of linear equations 2
bymath123a
 
PDF
5As Method of Lesson Plan on Ssolving systems of linear equations in two vari...
byElton John Embodo
 
PDF
Substitution Method of Systems of Linear Equations
bySonarin Cruz
 
PPTX
Solving systems of linear equations by substitution
byduanenestor
 
PPT
Solving systems of Linear Equations
byswartzje
 
PPTX
Linear equations
byNisarg Amin
 
PPT
Linear equations rev
byYash Jain
 
PPT
Pair of linear equations
byYash Jain
 
PPT
Linear equations rev - copy
byYash Jain
 
DOC
Mathematics 8 Systems of Linear Inequalities
byJuan Miguel Palero
 
PPT
Solving systems of equations by substitution
byEdrin Jay Morta
 
PPTX
LecturePresentation.pptx
byAlbertoPreciado10
 
PPTX
Beating the system (of equations)
byMatthew DeMoss
 
PPS
Alg1 ch0702example12(1)
byamymallory
 
PPT
Systems of Linear Equations
byalrosiemae
 
PPTX
How to solve linear equations by substitution
byJenaroDelgado1
 
PPT
Systems of equations and matricies
byST ZULAIHA NURHAJARURAHMAH
 
DOC
System of linear equations 2 eso
byEducación
 
PPTX
Lecture3
byHazel Joy Chong
 
PPT
7.2
bynglaze10
 
3 4 systems of linear equations 2
bymath123a
 
5As Method of Lesson Plan on Ssolving systems of linear equations in two vari...
byElton John Embodo
 
Substitution Method of Systems of Linear Equations
bySonarin Cruz
 
Solving systems of linear equations by substitution
byduanenestor
 
Solving systems of Linear Equations
byswartzje
 
Linear equations
byNisarg Amin
 
Linear equations rev
byYash Jain
 
Pair of linear equations
byYash Jain
 
Linear equations rev - copy
byYash Jain
 
Mathematics 8 Systems of Linear Inequalities
byJuan Miguel Palero
 
Solving systems of equations by substitution
byEdrin Jay Morta
 
LecturePresentation.pptx
byAlbertoPreciado10
 
Beating the system (of equations)
byMatthew DeMoss
 
Alg1 ch0702example12(1)
byamymallory
 
Systems of Linear Equations
byalrosiemae
 
How to solve linear equations by substitution
byJenaroDelgado1
 
Systems of equations and matricies
byST ZULAIHA NURHAJARURAHMAH
 
System of linear equations 2 eso
byEducación
 
Lecture3
byHazel Joy Chong
 
7.2
bynglaze10
 

More from Tzenma

PPTX
6 slopes and difference quotient x
byTzenma
 
PPTX
5 algebra of functions
byTzenma
 
PPTX
4 graphs of equations conic sections-circles
byTzenma
 
PPTX
3 graphs of second degree functions x
byTzenma
 
PPTX
2 graphs of first degree functions x
byTzenma
 
PPTX
1 functions
byTzenma
 
PPTX
9 rational equations word problems-x
byTzenma
 
PPTX
9 rational equations word problems-x
byTzenma
 
PPTX
7 proportions x
byTzenma
 
PPTX
10 complex fractions x
byTzenma
 
PPTX
6 addition and subtraction ii x
byTzenma
 
PPTX
5 addition and subtraction i x
byTzenma
 
PPTX
4 the lcm and clearing denominators x
byTzenma
 
PPTX
3 multiplication and division of rational expressions x
byTzenma
 
PPTX
2 cancellation x
byTzenma
 
PPTX
1 rational expressions x
byTzenma
 
PPTX
8 linear word problems in x&y x
byTzenma
 
PPTX
6 system of linear equations i x
byTzenma
 
PPTX
5 equations of lines x
byTzenma
 
PPTX
4 more on slopes x
byTzenma
 
6 slopes and difference quotient x
byTzenma
 
5 algebra of functions
byTzenma
 
4 graphs of equations conic sections-circles
byTzenma
 
3 graphs of second degree functions x
byTzenma
 
2 graphs of first degree functions x
byTzenma
 
1 functions
byTzenma
 
9 rational equations word problems-x
byTzenma
 
9 rational equations word problems-x
byTzenma
 
7 proportions x
byTzenma
 
10 complex fractions x
byTzenma
 
6 addition and subtraction ii x
byTzenma
 
5 addition and subtraction i x
byTzenma
 
4 the lcm and clearing denominators x
byTzenma
 
3 multiplication and division of rational expressions x
byTzenma
 
2 cancellation x
byTzenma
 
1 rational expressions x
byTzenma
 
8 linear word problems in x&y x
byTzenma
 
6 system of linear equations i x
byTzenma
 
5 equations of lines x
byTzenma
 
4 more on slopes x
byTzenma
 

Recently uploaded

PPTX
3 G8_Q3_L3_ (Cartoon as Representation in Opinion Editorial Article).pptx
byNorafeSahagun
 
PDF
M.Sc. Nonchordates Complete Syllabus PPT | All Important Topics Covered
byKNIPSS SULTANPUR
 
PDF
Analyzing the data of your initial survey
byThelma Villaflores
 
PPTX
How to Manage Package Reservation in Odoo 18 Inventory
byCeline George
 
PDF
Types of eggs and Egg membranes (Developmental Zoology)
bySudhandraKarthi
 
PPTX
Multiple Linear Regression - Least Square Method X₁ on X₂ and X₃
bySundar B N
 
PPTX
How to Track a Link Using Odoo 18 SMS Marketing
byCeline George
 
PPTX
PURPOSIVE SAMPLING IN EDUCATIONAL RESEARCH RACHITHRA RK.pptx
byssuser047b711
 
PDF
DHA/HAAD/MOH/DOH OPTOMETRY MCQ PYQ. .pdf
byAnmol Singh
 
PDF
Using Charts and Tables in Presenting Data
byThelma Villaflores
 
PDF
Biology Practical Class 12th 2025 PDF(2)-2-52.pdf
bySCPRPWomenCollegeChi
 
PPTX
AN EXTREMELY BORING GENERAL QUIZ FOR UG.pptx
bySriramG47
 
PPTX
Semester 6 Unit 2 Club foot (talipes).pptx
bysachin7989
 
PPTX
Repeat Orders_ Use Odoo Blanket Agreement
byCeline George
 
PPTX
Growth & Development MILESTONES (ADOLESCENTS ).pptx
byAneetaSharma15
 
PPTX
TAMIS & TEMS - HOW, WHY and THE STEPS IN PROCTOLOGY
byJohn Thanakumar
 
PDF
The Tale of Melon City poem ppt by Sahasra
bybitrasahasra
 
PDF
Cultivating Greatness Pune's Best Preschools and Schools.pdf
byWellington College
 
PPTX
Overview of how to Create a Model in Odoo 18
byCeline George
 
PDF
Risk management in Moroccan public hospitals_ a literature review
byMan_Ebook
 
3 G8_Q3_L3_ (Cartoon as Representation in Opinion Editorial Article).pptx
byNorafeSahagun
 
M.Sc. Nonchordates Complete Syllabus PPT | All Important Topics Covered
byKNIPSS SULTANPUR
 
Analyzing the data of your initial survey
byThelma Villaflores
 
How to Manage Package Reservation in Odoo 18 Inventory
byCeline George
 
Types of eggs and Egg membranes (Developmental Zoology)
bySudhandraKarthi
 
Multiple Linear Regression - Least Square Method X₁ on X₂ and X₃
bySundar B N
 
How to Track a Link Using Odoo 18 SMS Marketing
byCeline George
 
PURPOSIVE SAMPLING IN EDUCATIONAL RESEARCH RACHITHRA RK.pptx
byssuser047b711
 
DHA/HAAD/MOH/DOH OPTOMETRY MCQ PYQ. .pdf
byAnmol Singh
 
Using Charts and Tables in Presenting Data
byThelma Villaflores
 
Biology Practical Class 12th 2025 PDF(2)-2-52.pdf
bySCPRPWomenCollegeChi
 
AN EXTREMELY BORING GENERAL QUIZ FOR UG.pptx
bySriramG47
 
Semester 6 Unit 2 Club foot (talipes).pptx
bysachin7989
 
Repeat Orders_ Use Odoo Blanket Agreement
byCeline George
 
Growth & Development MILESTONES (ADOLESCENTS ).pptx
byAneetaSharma15
 
TAMIS & TEMS - HOW, WHY and THE STEPS IN PROCTOLOGY
byJohn Thanakumar
 
The Tale of Melon City poem ppt by Sahasra
bybitrasahasra
 
Cultivating Greatness Pune's Best Preschools and Schools.pdf
byWellington College
 
Overview of how to Create a Model in Odoo 18
byCeline George
 
Risk management in Moroccan public hospitals_ a literature review
byMan_Ebook
 

7 system of linear equations ii x

  • 1.
    Systems of LinearEquations II
  • 2.
    Systems of LinearEquations II Example A. At Pizza Grande, one coupon C may be exchanged for three slices of pizza (P) and five donuts (D). We have 5 slices of pizzas, 3 donuts and 2 coupons. What do we have after exchanging the 2 coupons?
  • 3.
    Systems of LinearEquations II Example A. At Pizza Grande, one coupon C may be exchanged for three slices of pizza (P) and five donuts (D). We have 5 slices of pizzas, 3 donuts and 2 coupons. What do we have after exchanging the 2 coupons? The coupon value of C may be recorded as C = 5P + 3D.
  • 4.
    Systems of LinearEquations II Example A. At Pizza Grande, one coupon C may be exchanged for three slices of pizza (P) and five donuts (D). We have 5 slices of pizzas, 3 donuts and 2 coupons. What do we have after exchanging the 2 coupons? The coupon value of C may be recorded as C = 5P + 3D. 5 slices of pizzas, 3 donuts and 2 coupons is 5P + 3D+ 2C.
  • 5.
    Systems of LinearEquations II Example A. At Pizza Grande, one coupon C may be exchanged for three slices of pizza (P) and five donuts (D). We have 5 slices of pizzas, 3 donuts and 2 coupons. What do we have after exchanging the 2 coupons? The coupon value of C may be recorded as C = 5P + 3D. 5 slices of pizzas, 3 donuts and 2 coupons is 5P + 3D+ 2C. Exchanging the 2 coupons for pizzas and donuts, we would have 5P + 3D + 2C
  • 6.
    Systems of LinearEquations II Example A. At Pizza Grande, one coupon C may be exchanged for three slices of pizza (P) and five donuts (D). We have 5 slices of pizzas, 3 donuts and 2 coupons. What do we have after exchanging the 2 coupons? The coupon value of C may be recorded as C = 5P + 3D. 5 slices of pizzas, 3 donuts and 2 coupons is 5P + 3D+ 2C. Exchanging the 2 coupons for pizzas and donuts, we would have 5P + 3D + 2C = 5P + 3D + 2(5P + 3D)
  • 7.
    Systems of LinearEquations II Example A. At Pizza Grande, one coupon C may be exchanged for three slices of pizza (P) and five donuts (D). We have 5 slices of pizzas, 3 donuts and 2 coupons. What do we have after exchanging the 2 coupons? The coupon value of C may be recorded as C = 5P + 3D. 5 slices of pizzas, 3 donuts and 2 coupons is 5P + 3D+ 2C. Exchanging the 2 coupons for pizzas and donuts, we would have 5P + 3D + 2C = 5P + 3D + 2(5P + 3D) = 5P + 3D + 10P + 6D
  • 8.
    Systems of LinearEquations II Example A. At Pizza Grande, one coupon C may be exchanged for three slices of pizza (P) and five donuts (D). We have 5 slices of pizzas, 3 donuts and 2 coupons. What do we have after exchanging the 2 coupons? The coupon value of C may be recorded as C = 5P + 3D. 5 slices of pizzas, 3 donuts and 2 coupons is 5P + 3D+ 2C. Exchanging the 2 coupons for pizzas and donuts, we would have 5P + 3D + 2C = 5P + 3D + 2(5P + 3D) = 5P + 3D + 10P + 6D = 15P + 9D or 15 slices of pizzas and 9 donuts.
  • 9.
    In math, thephrase "substitute (the expression) back into ...“ means to do the exchange, using the given coupon–expression, in the targeted equations, or expressions mentioned. Systems of Linear Equations II Example A. At Pizza Grande, one coupon C may be exchanged for three slices of pizza (P) and five donuts (D). We have 5 slices of pizzas, 3 donuts and 2 coupons. What do we have after exchanging the 2 coupons? The coupon value of C may be recorded as C = 5P + 3D. 5 slices of pizzas, 3 donuts and 2 coupons is 5P + 3D+ 2C. Exchanging the 2 coupons for pizzas and donuts, we would have 5P + 3D + 2C = 5P + 3D + 2(5P + 3D) = 5P + 3D + 10P + 6D = 15P + 9D or 15 slices of pizzas and 9 donuts.
  • 10.
    There are twoother methods to solve system of equations. Systems of Linear Equations II
  • 11.
    There are twoother methods to solve system of equations. Substitution Method Systems of Linear Equations II
  • 12.
    There are twoother methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation. Systems of Linear Equations II
  • 13.
    2x + y= 7 E1 x + y = 5 E2 Solve by the substitution method. Systems of Linear Equations II Example B. { There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation.
  • 14.
    2x + y= 7 E1 x + y = 5 E2 Solve by the substitution method. From E2, x + y = 5, we get x = 5 – y. Systems of Linear Equations II Example B. { There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation.
  • 15.
    2x + y= 7 E1 x + y = 5 E2 Solve by the substitution method. From E2, x + y = 5, we get x = 5 – y. Systems of Linear Equations II Example B. { There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation. This is the coupon expression so we may exchange x = 5 – y
  • 16.
    2x + y= 7 E1 x + y = 5 E2 Solve by the substitution method. From E2, x + y = 5, we get x = 5 – y. Then we replace x by (5 – y) in E1 and get 2(5 – y) + y = 7 Systems of Linear Equations II Example B. { There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation. This is the coupon expression so we may exchange x = 5 – y
  • 17.
    2x + y= 7 E1 x + y = 5 E2 Solve by the substitution method. From E2, x + y = 5, we get x = 5 – y. Then we replace x by (5 – y) in E1 and get 2(5 – y) + y = 7 10 – 2y + y = 7 Systems of Linear Equations II Example B. { There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation. This is the coupon expression so we may exchange x = 5 – y
  • 18.
    2x + y= 7 E1 x + y = 5 E2 Solve by the substitution method. From E2, x + y = 5, we get x = 5 – y. Then we replace x by (5 – y) in E1 and get 2(5 – y) + y = 7 10 – 2y + y = 7 10 – y = 7  3 = y Systems of Linear Equations II Example B. { There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation. This is the coupon expression so we may exchange x = 5 – y
  • 19.
    2x + y= 7 E1 x + y = 5 E2 Solve by the substitution method. From E2, x + y = 5, we get x = 5 – y. Then we replace x by (5 – y) in E1 and get 2(5 – y) + y = 7 10 – 2y + y = 7 10 – y = 7  3 = y Systems of Linear Equations II Example B. { Put 3 = y back to E2 to find x, we get x + 3 = 5 There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation. This is the coupon expression so we may exchange x = 5 – y
  • 20.
    2x + y= 7 E1 x + y = 5 E2 Solve by the substitution method. From E2, x + y = 5, we get x = 5 – y. Then we replace x by (5 – y) in E1 and get 2(5 – y) + y = 7 10 – 2y + y = 7 10 – y = 7  3 = y Systems of Linear Equations II Example B. { Put 3 = y back to E2 to find x, we get x + 3 = 5  x = 2 Therefore the solution is (2, 3) There are two other methods to solve system of equations. Substitution Method In substitution method, we solve for one of the variables in terms of the other, then substitute the result into the other equation. This is the coupon expression so we may exchange x = 5 – y
  • 21.
    We use thesubstitution method when it's easy to solve for one of the variable in terms of the other. Systems of Linear Equations II
  • 22.
    We use thesubstitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. Systems of Linear Equations II
  • 23.
    We use thesubstitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. Systems of Linear Equations II Example C. {
  • 24.
    We use thesubstitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. By inspection, we see that it's easy to solve for the y using E1. Systems of Linear Equations II Example C. {
  • 25.
    We use thesubstitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. By inspection, we see that it's easy to solve for the y using E1. From E1, 2x – y = 7, we get 2x – 7= y. Systems of Linear Equations II Example C. {
  • 26.
    We use thesubstitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. By inspection, we see that it's easy to solve for the y using E1. From E1, 2x – y = 7, we get 2x – 7= y. Substitute y by (2x – 7) in E2 and get 3x + 2(2x – 7) = 7 Systems of Linear Equations II Example C. {
  • 27.
    We use thesubstitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. By inspection, we see that it's easy to solve for the y using E1. From E1, 2x – y = 7, we get 2x – 7= y. Substitute y by (2x – 7) in E2 and get 3x + 2(2x – 7) = 7 3x + 4x – 14 = 7 Systems of Linear Equations II Example C. {
  • 28.
    We use thesubstitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. By inspection, we see that it's easy to solve for the y using E1. From E1, 2x – y = 7, we get 2x – 7= y. Substitute y by (2x – 7) in E2 and get 3x + 2(2x – 7) = 7 3x + 4x – 14 = 7 7x = 21 x = 3 Systems of Linear Equations II Example C. {
  • 29.
    We use thesubstitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. By inspection, we see that it's easy to solve for the y using E1. From E1, 2x – y = 7, we get 2x – 7= y. Substitute y by (2x – 7) in E2 and get 3x + 2(2x – 7) = 7 3x + 4x – 14 = 7 7x = 21 x = 3 Systems of Linear Equations II Example C. { To find y, use the substitution equation, set x = 3 in y = 2x – 7
  • 30.
    We use thesubstitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. By inspection, we see that it's easy to solve for the y using E1. From E1, 2x – y = 7, we get 2x – 7= y. Substitute y by (2x – 7) in E2 and get 3x + 2(2x – 7) = 7 3x + 4x – 14 = 7 7x = 21 x = 3 Systems of Linear Equations II Example C. { To find y, use the substitution equation, set x = 3 in y = 2x – 7 y = 2(3) – 7 y = -1
  • 31.
    We use thesubstitution method when it's easy to solve for one of the variable in terms of the other. Specifically, it is easy to solve for a variable when an equation contains an single x or single y. 2x – y = 7 E1 3x + 2y = 7 E2 Solve by the substitution method. By inspection, we see that it's easy to solve for the y using E1. From E1, 2x – y = 7, we get 2x – 7= y. Substitute y by (2x – 7) in E2 and get 3x + 2(2x – 7) = 7 3x + 4x – 14 = 7 7x = 21 x = 3 Systems of Linear Equations II Example C. { To find y, use the substitution equation, set x = 3 in y = 2x – 7 y = 2(3) – 7 y = -1 Hence the solution is (3, -1).
  • 32.
    Graphing Method Systems ofLinear Equations II
  • 33.
    Graphing Method Given asystem of linear equations the graph of each equation is a straight line. Systems of Linear Equations II
  • 34.
    Graphing Method Given asystem of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Systems of Linear Equations II
  • 35.
    Graphing Method Given asystem of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. Systems of Linear Equations II
  • 36.
    Graphing Method Given asystem of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II
  • 37.
    Graphing Method Given asystem of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D.
  • 38.
    Graphing Method Given asystem of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method.
  • 39.
    Graphing Method Given asystem of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x y 0 0 2x + y = 7
  • 40.
    Graphing Method Given asystem of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x y 0 7 0 2x + y = 7
  • 41.
    Graphing Method Given asystem of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x y 0 7 7/2 0 2x + y = 7 E2
  • 42.
    Graphing Method Given asystem of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x y 0 7 7/2 0 2x + y = 7 E2 (Check another point.)
  • 43.
    Graphing Method Given asystem of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x y 0 7 7/2 0 2x + y = 7 E1 E2 (0, 7) (7/2, 0) E1(Check another point.)
  • 44.
    Graphing Method Given asystem of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x + y = 5 x y 0 7 7/2 0 2x + y = 7 x y 0 0 (0, 7) (7/2, 0) E1(Check another point.)
  • 45.
    Graphing Method Given asystem of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x y 0 7 7/2 0 2x + y = 7 x + y = 5 x y 0 5 5 0 (0, 7) (7/2, 0) E1(Check another point.)
  • 46.
    Graphing Method Given asystem of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x y 0 7 7/2 0 2x + y = 7 (0, 7) (7/2, 0) (0, 5) (5, 0) E2 x + y = 5 x y 0 5 5 0 E1(Check another point.)
  • 47.
    Graphing Method Given asystem of linear equations the graph of each equation is a straight line. The solution of the system is the intersection point (x, y) of the these lines. Thus we may find the solution by graphing the lines and locate the point of intersection graphically. In general, we don't not use the graphing method because it is not easy to do it accurately. Systems of Linear Equations II 2x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example D. Use intercept method. x y 0 7 7/2 0 2x + y = 7 (0, 7) (7/2, 0) (0, 5) (5, 0) The intersection (2, 3) is the solution E1 E2 x + y = 5 x y 0 5 5 0 E1(Check another point.)
  • 48.
    Graphing of inconsistentsystems are parallel lines which do not intersect, hence there is no solution. Systems of Linear Equations II
  • 49.
    Graphing of inconsistentsystems are parallel lines which do not intersect, hence there is no solution. Systems of Linear Equations II x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example E.
  • 50.
    Graphing of inconsistentsystems are parallel lines which do not intersect, hence there is no solution. x + y = 7 x y 0 7 7 0 Systems of Linear Equations II x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example E.
  • 51.
    Graphing of inconsistentsystems are parallel lines which do not intersect, hence there is no solution. x + y = 7 x y 0 7 7 0 (0, 7) (7, 0) Systems of Linear Equations II x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example E.
  • 52.
    Graphing of inconsistentsystems are parallel lines which do not intersect, hence there is no solution. x + y = 7 x y 0 7 7 0 x y 0 5 5 0 (0, 7) (7, 0) Systems of Linear Equations II x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example E. x + y = 5
  • 53.
    Graphing of inconsistentsystems are parallel lines which do not intersect, hence there is no solution. x + y = 7 x y 0 7 7 0 x y 0 5 5 0 (0, 7) (7, 0) (0, 5) (5, 0) Systems of Linear Equations II x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example E. x + y = 5
  • 54.
    Graphing of inconsistentsystems are parallel lines which do not intersect, hence there is no solution. x + y = 7 x y 0 7 7 0 x y 0 5 5 0 (0, 7) (7, 0) (0, 5) (5, 0) No intersection. No solution Systems of Linear Equations II x + y = 7 x + y = 5 Solve graphically.{ E1 E2 Example E. x + y = 5
  • 55.
    Graphs of dependentsystems are identical lines, hence every point on the line is a solution. Systems of Linear Equations II
  • 56.
    Graphs of dependentsystems are identical lines, hence every point on the line is a solution. Systems of Linear Equations II x + y = 5 2x + 2y = 10 Solve graphically.{ E1 E2Example F.
  • 57.
    Graphs of dependentsystems are identical lines, hence every point on the line is a solution. 2x + 2y = 10 is the same as x + y = 5 Systems of Linear Equations II x + y = 5 2x + 2y = 10 Solve graphically.{ E1 E2Example F.
  • 58.
    Graphs of dependentsystems are identical lines, hence every point on the line is a solution. 2x + 2y = 10 is the same as x + y = 5 x y 0 5 5 0 Systems of Linear Equations II x + y = 5 2x + 2y = 10 Solve graphically.{ E1 E2Example F.
  • 59.
    Graphs of dependentsystems are identical lines, hence every point on the line is a solution. 2x + 2y = 10 is the same as x + y = 5 x y 0 5 5 0 (5, 0) (0, 5) Systems of Linear Equations II x + y = 5 2x + 2y = 10 Solve graphically.{ E1 E2Example F.
  • 60.
    Graphs of dependentsystems are identical lines, hence every point on the line is a solution. 2x + 2y = 10 is the same as x + y = 5 x y 0 5 5 0 (5, 0) (0, 5) Every point is a solution, e.g.(0, 5), (2, 3), (5, 0)… (2, 3) Systems of Linear Equations II x + y = 5 2x + 2y = 10 Solve graphically.{ E1 E2Example F.
  • 61.
    Systems of LinearEquations II 4. {–x + 2y = –12 y = 4 – 2x Exercise. Solve by the substitution method. 1. {y = 3 – x 2x + y = 4 2. 3. {x = 3 – y 2x – y = 6 {x + y = 3 2x + 6 = y 5. {3x + 4y = 3 x = 6 + 2y 6. { x = 3 – 3y 2x – 9y = –4 10. Graph the inconsistent system { x + 3y = 4 2x + 6y = 8 {2x – y = 2 8x – 4y = 6 Problem 7, 8, 9: Solve problem 1, 2, and 3 by graphing. 11. Graph the dependent system