The document discusses the basic language of functions. A function assigns each input exactly one output. Functions can be defined through written instructions, tables, or mathematical formulas. The domain is the set of all inputs, and the range is the set of all outputs. Functions are widely used in mathematics to model real-world relationships.

1. The Basic Language of Functions

2. The Basic Language of Functions
A function is a procedure that assigns each input
exactly one output.

3. The Basic Language of Functions
A function is a procedure that assigns each input
exactly one output. In mathematics, usually we name
functions as f, g, h…

4. The Basic Language of Functions
A function is a procedure that assigns each input
exactly one output. In mathematics, usually we name
functions as f, g, h…and we let x represent the input
and y represent the output y.

5. Example A:
a. Input a number x, the output is (are)
whole number(s) within ¾ of x. Is this a function?
The Basic Language of Functions
A function is a procedure that assigns each input
exactly one output. In mathematics, usually we name
functions as f, g, h…and we let x represent the input
and y represent the output y.

6. Example A:
a. Input a number x, the output is (are)
whole number(s) within ¾ of x. Is this a function?
No, this is not a function because if x = ½, there'll be
two different outputs 0 or 1.
The Basic Language of Functions
A function is a procedure that assigns each input
exactly one output. In mathematics, usually we name
functions as f, g, h…and we let x represent the input
and y represent the output y.

7. Example A:
a. Input a number x, the output is (are)
whole number(s) within ¾ of x. Is this a function?
No, this is not a function because if x = ½, there'll be
two different outputs 0 or 1.
The Basic Language of Functions
b. Input a number x, the output is the largest integer
less than or equal to x. Is this a function?
A function is a procedure that assigns each input
exactly one output. In mathematics, usually we name
functions as f, g, h…and we let x represent the input
and y represent the output y.

8. Example A:
a. Input a number x, the output is (are)
whole number(s) within ¾ of x. Is this a function?
No, this is not a function because if x = ½, there'll be
two different outputs 0 or 1.
The Basic Language of Functions
b. Input a number x, the output is the largest integer
less than or equal to x. Is this a function?
This is a function. Its called the greatest integer
function and it’s denoted as [x].
A function is a procedure that assigns each input
exactly one output. In mathematics, usually we name
functions as f, g, h…and we let x represent the input
and y represent the output y.

9. Example A:
a. Input a number x, the output is (are)
whole number(s) within ¾ of x. Is this a function?
No, this is not a function because if x = ½, there'll be
two different outputs 0 or 1.
The Basic Language of Functions
b. Input a number x, the output is the largest integer
less than or equal to x. Is this a function?
This is a function. Its called the greatest integer
function and it’s denoted as [x]. (so [3.1] = [3] = 3.).
A function is a procedure that assigns each input
exactly one output. In mathematics, usually we name
functions as f, g, h…and we let x represent the input
and y represent the output y.

10. Given a function, the set D of all the inputs is called
the domain of the function,
The Basic Language of Functions

11. Given a function, the set D of all the inputs is called
the domain of the function, the set R of all the outputs
is called the range of the function.
The Basic Language of Functions

12. Given a function, the set D of all the inputs is called
the domain of the function, the set R of all the outputs
is called the range of the function. The domain D of [x]
is the set of all real numbers.
The Basic Language of Functions

13. Given a function, the set D of all the inputs is called
the domain of the function, the set R of all the outputs
is called the range of the function. The domain D of [x]
is the set of all real numbers. The range R of [x] is the
set of all integers.
The Basic Language of Functions

14. Given a function, the set D of all the inputs is called
the domain of the function, the set R of all the outputs
is called the range of the function. The domain D of [x]
is the set of all real numbers. The range R of [x] is the
set of all integers. There are many ways to define
functions.
The Basic Language of Functions

15. Given a function, the set D of all the inputs is called
the domain of the function, the set R of all the outputs
is called the range of the function. The domain D of [x]
is the set of all real numbers. The range R of [x] is the
set of all integers. There are many ways to define
functions. Functions may be defined by written
instructions such as [x] above.
The Basic Language of Functions

16. Given a function, the set D of all the inputs is called
the domain of the function, the set R of all the outputs
is called the range of the function. The domain D of [x]
is the set of all real numbers. The range R of [x] is the
set of all integers. There are many ways to define
functions. Functions may be defined by written
instructions such as [x] above. Functions may be
given a table as shown.
The Basic Language of Functions
x y
–1 4
2 3
5 –3
6 4
7 2

17. Given a function, the set D of all the inputs is called
the domain of the function, the set R of all the outputs
is called the range of the function. The domain D of [x]
is the set of all real numbers. The range R of [x] is the
set of all integers. There are many ways to define
functions. Functions may be defined by written
instructions such as [x] above. Functions may be
given a table as shown. With this
table we see that 3 is the output for
the input 2,
The Basic Language of Functions
x y
–1 4
2 3
5 –3
6 4
7 2

18. Given a function, the set D of all the inputs is called
the domain of the function, the set R of all the outputs
is called the range of the function. The domain D of [x]
is the set of all real numbers. The range R of [x] is the
set of all integers. There are many ways to define
functions. Functions may be defined by written
instructions such as [x] above. Functions may be
given a table as shown. With this
table we see that 3 is the output for
the input 2, and
the domain D = {–1, 2, 5, 6, 7},
The Basic Language of Functions
x y
–1 4
2 3
5 –3
6 4
7 2

19. Given a function, the set D of all the inputs is called
the domain of the function, the set R of all the outputs
is called the range of the function. The domain D of [x]
is the set of all real numbers. The range R of [x] is the
set of all integers. There are many ways to define
functions. Functions may be defined by written
instructions such as [x] above. Functions may be
given a table as shown. With this
table we see that 3 is the output for
the input 2, and
the domain D = {–1, 2, 5, 6, 7},
the range is R = {4, 3, –3, 2}.
The Basic Language of Functions
x y
–1 4
2 3
5 –3
6 4
7 2

20. Given a function, the set D of all the inputs is called
the domain of the function, the set R of all the outputs
is called the range of the function. The domain D of [x]
is the set of all real numbers. The range R of [x] is the
set of all integers. There are many ways to define
functions. Functions may be defined by written
instructions such as [x] above. Functions may be
given a table as shown. With this
table we see that 3 is the output for
the input 2, and
the domain D = {–1, 2, 5, 6, 7},
the range is R = {4, 3, –3, 2}.
Note that we may have the same output
4 for two different inputs –1 and 6.
The Basic Language of Functions
x y
–1 4
2 3
5 –3
6 4
7 2

21. Functions may be given graphically:
The Basic Language of Functions

22. Functions may be given graphically:
For instance, Nominal Price(1975)  $0.50
The Basic Language of Functions

23. Functions may be given graphically:
Domain = {year 1918  2005}
For instance, Nominal Price(1975)  $0.50
The Basic Language of Functions

24. Functions may be given graphically:
Domain = {year 1918  2005}
Range (Nominal Price) = {$0.20$2.51}
For instance, Nominal Price(1975)  $1.00
The Basic Language of Functions

25. The Basic Language of Functions
Functions may be given graphically:
Inflation Adjusted Price(1975)  $1.85

26. The Basic Language of Functions
Functions may be given graphically:
Domain = {year 1918  2005}
Inflation Adjusted Price(1975)  $1.85

27. The Basic Language of Functions
Functions may be given graphically:
Domain = {year 1918  2005}
Range (Inflation Adjusted Price) = {$1.25$3.50}
Inflation Adjusted Price(1975)  $1.85

28. The Basic Language of Functions
Most functions are given by mathematics formulas.

29. For example,
f(X) = X2 – 2X + 3 = y
The Basic Language of Functions
Most functions are given by mathematics formulas.

30. For example,
f(X) = X2 – 2X + 3 = y
name of
the function
The Basic Language of Functions
Most functions are given by mathematics formulas.

31. For example,
f(X) = X2 – 2X + 3 = y
name of
the function
The Basic Language of Functions
Most functions are given by mathematics formulas.
input box

32. For example,
f(X) = X2 – 2X + 3 = y
name of actual formula
the function
The Basic Language of Functions
Most functions are given by mathematics formulas.
input box

33. For example,
f(X) = X2 – 2X + 3 = y
name of actual formula
the function
The output
The Basic Language of Functions
Most functions are given by mathematics formulas.
input box

34. For example,
f(X) = X2 – 2X + 3 = y
name of actual formula
the function
The output
The Basic Language of Functions
Most functions are given by mathematics formulas.
input box
The input box holds the input for the formula.

35. For example,
f(X) = X2 – 2X + 3 = y
name of actual formula
the function
The output
The Basic Language of Functions
Most functions are given by mathematics formulas.
input box
The input box holds the input for the formula.
Hence f (2) means to replace x by (2) in the formula,
so f(2) = (2)2 – 2(2) + 3 = 3 = y.

36. For example,
f(X) = X2 – 2X + 3 = y
name of actual formula
the function
The output
The Basic Language of Functions
Most functions are given by mathematics formulas.
input box
The input box holds the input for the formula.
Hence f (2) means to replace x by (2) in the formula,
so f(2) = (2)2 – 2(2) + 3 = 3 = y.
The domain of this f(x) is the set of all real numbers.

37. For example,
f(X) = X2 – 2X + 3 = y
name of actual formula
the function
The output
The Basic Language of Functions
Most functions are given by mathematics formulas.
input box
The input box holds the input for the formula.
Hence f (2) means to replace x by (2) in the formula,
so f(2) = (2)2 – 2(2) + 3 = 3 = y.
The above function notation is used with the +, –, /,
and * with the obvious interpretation.
The domain of this f(x) is the set of all real numbers.

38. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3.
a. Evaluate f(–2)

39. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3.
a. Evaluate f(–2)
f(x) = –3x + 2

40. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3.
a. Evaluate f(–2)
f(x) = –3x + 2
f(–2)

41. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3.
a. Evaluate f(–2)
f(x) = –3x + 2
f(–2)
copy the input

42. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3.
a. Evaluate f(–2)
f(x) = –3x + 2
f(–2)
copy the input then paste the input
at where the x is

43. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3.
a. Evaluate f(–2)
f(x) = –3x + 2
f(–2) = –3(–2) + 2

44. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3x + 1.
a. Evaluate f(–2).
f(–2) = –3(–2) – 3 = 3

45. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3x + 1.
a. Evaluate f(–2).
f(–2) = –3(–2) – 3 = 3
b. Evaluate g(–2).

46. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3x + 1.
a. Evaluate f(–2).
f(–2) = –3(–2) – 3 = 3
b. Evaluate g(–2).
g(x) = –2x2 – 3x + 1

47. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3x + 1.
a. Evaluate f(–2).
f(–2) = –3(–2) – 3 = 3
b. Evaluate g(–2).
g(x) = –2x2 – 3x + 1
g(–2)

48. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3x + 1.
a. Evaluate f(–2).
f(–2) = –3(–2) – 3 = 3
b. Evaluate g(–2).
g(x) = –2x2 – 3x + 1
g(–2)
copy the input

49. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3x + 1.
a. Evaluate f(–2).
f(–2) = –3(–2) – 3 = 3
b. Evaluate g(–2).
g(x) = –2x2 – 3x + 1
g(–2)
copy the input
then paste the input
at where the x’s are

50. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3x + 1.
a. Evaluate f(–2).
f(–2) = –3(–2) – 3 = 3
b. Evaluate g(–2).
g(x) = –2x2 – 3x + 1
g(–2) = –2(–2)2 – 3(–2) + 1
copy the input

51. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3x + 1.
a. Evaluate f(–2).
f(–2) = –3(–2) – 3 = 3
b. Evaluate g(–2).
g(–2) = –2(–2)2 – 3(–2) + 1

52. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3x + 1.
a. Evaluate f(–2).
f(–2) = –3(–2) – 3 = 3
b. Evaluate g(–2).
g(–2) = –2(–2)2 – 3(–2) + 1
= –8 + 6 + 1 = –1

53. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3x + 1.
a. Evaluate f(–2).
f(–2) = –3(–2) – 3 = 3
b. Evaluate g(–2).
g(–2) = –2(–2)2 – 3(–2) + 1
= –8 + 6 + 1 = –1
c. Evaluate f(–2) – g(–2).

54. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3x + 1.
a. Evaluate f(–2).
f(–2) = –3(–2) – 3 = 3
b. Evaluate g(–2).
g(–2) = –2(–2)2 – 3(–2) + 1
= –8 + 6 + 1 = –1
c. Evaluate f(–2) – g(–2).
Using the outputs of parts a and b we’ve
f(–2) – g(–2)
=

55. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3x + 1.
a. Evaluate f(–2).
f(–2) = –3(–2) – 3 = 3
b. Evaluate g(–2).
g(–2) = –2(–2)2 – 3(–2) + 1
= –8 + 6 + 1 = –1
c. Evaluate f(–2) – g(–2).
Using the outputs of parts a and b we’ve
f(–2) – g(–2)
= 3 – (–1) = 4

56. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3x + 1.
a. Evaluate f(–2).
f(–2) = –3(–2) – 3 = 3
b. Evaluate g(–2).
g(–2) = –2(–2)2 – 3(–2) + 1
= –8 + 6 + 1 = –1
c. Evaluate f(–2) – g(–2).
Using the outputs of parts a and b we’ve
f(–2) – g(–2)
= 3 – (–1) = 4
The function f(x) = c where c is a number is called
a constant function.

57. The Basic Language of Functions
Example B. Let f(x) = –3x + 2, g(x) = –2x2 – 3x + 1.
a. Evaluate f(–2).
f(–2) = –3(–2) – 3 = 3
b. Evaluate g(–2).
g(–2) = –2(–2)2 – 3(–2) + 1
= –8 + 6 + 1 = –1
c. Evaluate f(–2) – g(–2).
Using the outputs of parts a and b we’ve
f(–2) – g(–2)
= 3 – (–1) = 4
The function f(x) = c where c is a number is called
a constant function. The outputs of such functions
do not change.

58. There are two main things to consider when
determining the domains of functions of real numbers.
The Basic Language of Functions

59. There are two main things to consider when
determining the domains of functions of real numbers.
1. The denominators can't be 0
The Basic Language of Functions

60. There are two main things to consider when
determining the domains of functions of real numbers.
1. The denominators can't be 0
2. The radicand of square root (or any even root)
can't be negative.
The Basic Language of Functions

61. There are two main things to consider when
determining the domains of functions of real numbers.
1. The denominators can't be 0
2. The radicand of square root (or any even root)
can't be negative.
Example C. Find the domain of the following functions.
a. f(x) = 1/(2x + 6)
b. f (X) =  2x + 6
The Basic Language of Functions

62. There are two main things to consider when
determining the domains of functions of real numbers.
1. The denominators can't be 0
2. The radicand of square root (or any even root)
can't be negative.
Example C. Find the domain of the following functions.
a. f(x) = 1/(2x + 6)
The denominator can’t be 0
b. f (X) =  2x + 6
The Basic Language of Functions

63. There are two main things to consider when
determining the domains of functions of real numbers.
1. The denominators can't be 0
2. The radicand of square root (or any even root)
can't be negative.
Example C. Find the domain of the following functions.
a. f(x) = 1/(2x + 6)
The denominator can’t be 0 i.e. 2x + 6 = 0  x = -3
b. f (X) =  2x + 6
The Basic Language of Functions

64. There are two main things to consider when
determining the domains of functions of real numbers.
1. The denominators can't be 0
2. The radicand of square root (or any even root)
can't be negative.
Example C. Find the domain of the following functions.
a. f(x) = 1/(2x + 6)
The denominator can’t be 0 i.e. 2x + 6 = 0  x = -3
So the domain = {all numbers except x = -3}.
b. f (X) =  2x + 6
The Basic Language of Functions

65. There are two main things to consider when
determining the domains of functions of real numbers.
1. The denominators can't be 0
2. The radicand of square root (or any even root)
can't be negative.
Example C. Find the domain of the following functions.
a. f(x) = 1/(2x + 6)
The denominator can’t be 0 i.e. 2x + 6 = 0  x = -3
So the domain = {all numbers except x = -3}.
b. f (X) =  2x + 6
We must have square root of nonnegative numbers.
The Basic Language of Functions

66. There are two main things to consider when
determining the domains of functions of real numbers.
1. The denominators can't be 0
2. The radicand of square root (or any even root)
can't be negative.
Example C. Find the domain of the following functions.
a. f(x) = 1/(2x + 6)
The denominator can’t be 0 i.e. 2x + 6 = 0  x = -3
So the domain = {all numbers except x = -3}.
b. f (X) =  2x + 6
We must have square root of nonnegative numbers.
Hence 2x + 6 > 0  x > -3
The Basic Language of Functions

67. There are two main things to consider when
determining the domains of functions of real numbers.
1. The denominators can't be 0
2. The radicand of square root (or any even root)
can't be negative.
Example C. Find the domain of the following functions.
a. f(x) = 1/(2x + 6)
The denominator can’t be 0 i.e. 2x + 6 = 0  x = -3
So the domain = {all numbers except x = -3}.
b. f (X) =  2x + 6
We must have square root of nonnegative numbers.
Hence 2x + 6 > 0  x > -3
So the domain = {all numbers x > -3}
The Basic Language of Functions

68. The Basic Language of Functions
Graphs of Functions

69. The Basic Language of Functions
Graphs of Functions
The plot of all points (x, y)’s
that satisfy a given function
y = f(x) is the graph of the
function y = f(x).

70. The Basic Language of Functions
Graphs of Functions
The plot of all points (x, y)’s
that satisfy a given function
y = f(x) is the graph of the
function y = f(x).
For example, let the function
f(x) = x + 1,

71. The Basic Language of Functions
Graphs of Functions
The plot of all points (x, y)’s
that satisfy a given function
y = f(x) is the graph of the
function y = f(x).
For example, let the function
f(x) = x + 1, set y = f(x) and
make a table of few of the
ordered pairs (x, y)’s that
satisfy the equation y = f(x).

72. The Basic Language of Functions
Graphs of Functions
The plot of all points (x, y)’s
that satisfy a given function
y = f(x) is the graph of the
function y = f(x).
For example, let the function
f(x) = x + 1, set y = f(x) and
make a table of few of the
ordered pairs (x, y)’s that
satisfy the equation y = f(x).
x 0 1 2 3
y = f(x) 1 2 3 4

73. The Basic Language of Functions
Graphs of Functions
The plot of all points (x, y)’s
that satisfy a given function
y = f(x) is the graph of the
function y = f(x).
For example, let the function
f(x) = x + 1, set y = f(x) and
make a table of few of the
ordered pairs (x, y)’s that
satisfy the equation y = f(x).
x 0 1 2 3
y = f(x) 1 2 3 4
Plot the (x, y)’s and we have the graph of f(x) = x + 1,
a line.

74. The Basic Language of Functions
Graphs of Functions
The plot of all points (x, y)’s
that satisfy a given function
y = f(x) is the graph of the
function y = f(x).
For example, let the function
f(x) = x + 1, set y = f(x) and
make a table of few of the
ordered pairs (x, y)’s that
satisfy the equation y = f(x).
x 0 1 2 3
y = f(x) 1 2 3 4
y = x + 1
Plot the (x, y)’s and we have the graph of f(x) = x + 1,
a line.

75. The Basic Language of Functions
Graphs of Functions
The plot of all points (x, y)’s
that satisfy a given function
y = f(x) is the graph of the
function y = f(x).
For example, let the function
f(x) = x + 1, set y = f(x) and
make a table of few of the
ordered pairs (x, y)’s that
satisfy the equation y = f(x).
x 0 1 2 3
y = f(x) 1 2 3 4
y = x + 1
Plot the (x, y)’s and we have the graph of f(x) = x + 1,
a line. Note that the graph of a function may cross any
vertical line at most at one point because for each x
there is only one corresponding output y.

76. The Basic Language of Functions
Graphs of Functions
The plot of all points (x, y)’s
that satisfy a given function
y = f(x) is the graph of the
function y = f(x).
For example, let the function
f(x) = x + 1, set y = f(x) and
make a table of few of the
ordered pairs (x, y)’s that
satisfy the equation y = f(x).
x 0 1 2 3
y = f(x) 1 2 3 4
y = x + 1
Plot the (x, y)’s and we have the graph of f(x) = x + 1,
a line. Note that the graph of a function may cross any
vertical line at most at one point because for each x
there is only one corresponding output y.

77. The Basic Language of Functions
The equation x = y2, treating x
as the input, is not a function.

78. The Basic Language of Functions
The equation x = y2, treating x
as the input, is not a function.
For instance, for the input
x = 4, there are two outputs
y’s that satisfy 4 = y2,

79. The Basic Language of Functions
The equation x = y2, treating x
as the input, is not a function.
For instance, for the input
x = 4, there are two outputs
y’s that satisfy 4 = y2, namely
y = 2 and y = –2.

80. The Basic Language of Functions
The equation x = y2, treating x
as the input, is not a function.
For instance, for the input
x = 4, there are two outputs
y’s that satisfy 4 = y2, namely
y = 2 and y = –2. So x = y2 is
not a function.

81. The Basic Language of Functions
The equation x = y2, treating x
as the input, is not a function.
For instance, for the input
x = 4, there are two outputs
y’s that satisfy 4 = y2, namely
y = 2 and y = –2. So x = y2 is
not a function.
Plot the graph by the table
shown.
x 0 1 1 4 4
y 0 1 -1 2 -2

82. The Basic Language of Functions
The equation x = y2, treating x
as the input, is not a function.
For instance, for the input
x = 4, there are two outputs
y’s that satisfy 4 = y2, namely
y = 2 and y = –2. So x = y2 is
not a function.
Plot the graph by the table
shown.
x 0 1 1 4 4
y 0 1 -1 2 -2
x 0 1 1 4 4
y 0 1 -1 2 -2
x = y2

83. The Basic Language of Functions
The equation x = y2, treating x
as the input, is not a function.
For instance, for the input
x = 4, there are two outputs
y’s that satisfy 4 = y2, namely
y = 2 and y = –2. So x = y2 is
not a function.
Plot the graph by the table
shown. In particular that if we
draw the vertical line x = 4,
x 0 1 1 4 4
y 0 1 -1 2 -2
x 0 1 1 4 4
y 0 1 -1 2 -2
x = y2
it intersects the graph at two points (4, 2) and (4, –2).

84. The Basic Language of Functions
The equation x = y2, treating x
as the input, is not a function.
For instance, for the input
x = 4, there are two outputs
y’s that satisfy 4 = y2, namely
y = 2 and y = –2. So x = y2 is
not a function.
Plot the graph by the table
shown. In particular that if we
draw the vertical line x = 4,
x 0 1 1 4 4
y 0 1 -1 2 -2
x 0 1 1 4 4
y 0 1 -1 2 -2
x = y2
it intersects the graph at two points (4, 2) and (4, –2).
In general if any vertical line crosses a graph at two
or more points then the graph does not represent any
function.

85. The Basic Language of Functions
Since for functions each
input x has exactly one
output, therefore each
vertical line can only
intersect it’s graph at exactly
one location (e.g. y = x + 1).

86. The Basic Language of Functions
Since for functions each
input x has exactly one
output, therefore each
vertical line can only
intersect it’s graph at exactly
one location (e.g. y = x + 1).
y = x + 1

87. The Basic Language of Functions
Since for functions each
input x has exactly one
output, therefore each
vertical line can only
intersect it’s graph at exactly
one location (e.g. y = x + 1).
y = x + 1
However, if any vertical line
intersects a graph at two or
more points, i.e. there are two
or more outputs y associated
to one input x (eg. x = y2),

88. The Basic Language of Functions
Since for functions each
input x has exactly one
output, therefore each
vertical line can only
intersect it’s graph at exactly
one location (e.g. y = x + 1).
y = x + 1
However, if any vertical line
intersects a graph at two or
more points, i.e. there are two
or more outputs y associated
to one input x (eg. x = y2),
then the graph must not be
the graph of a function.

89. The Basic Language of Functions
Since for functions each
input x has exactly one
output, therefore each
vertical line can only
intersect it’s graph at exactly
one location (e.g. y = x + 1).
x 0 1 1 4 4
y 0 1 -1 2 -2
y = x + 1
However, if any vertical line
intersects a graph at two or
more points, i.e. there are two
or more outputs y associated
to one input x (eg. x = y2),
then the graph must not be
the graph of a function.

90. The Basic Language of Functions
Exercise A. For problems 1 – 6, determine if the
given represents a function. If it’s not a function,
give a reason why it’s not.
x y
2 4
2 3
4 3
1. x y
2 4
3 4
4 4
2. 3. 4.
x
y y
6. For any real number input x that is a rational
number, the output is 0, otherwise the output is 1
5. For any input x that is a positive integer, the
outputs are it’s factors.
x
All the (x, y)’s on the curve

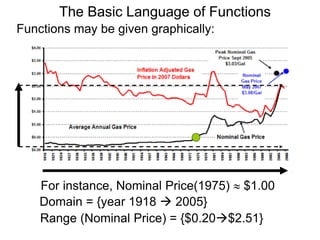
91. The Basic Language of Functions
Exercise B.
Given the functions
f, g and h, find the
outcomes of the
following expressions.
If it’s not defined,
state so.
x y = g(x)
–1 4
2 3
5 –3
6 4
7 2
y = h(x)
f(x) = –3x + 7
7. f(–1) 8.g(–1) 9.h(–1)
10. –f(3) 11. –g(3) 12. –h(3)
13. 3g(6) 14.2f(2) 15. h(3) + h(0)
16. 2f(4) + 3g(2) 17. –f(4) + f(–4) 18. h(6)*[f(2)]2

92. The Basic Language of Functions
19. f(x) =
1
2x – 6 20. f (x) =  2x – 6
Exercise C. Find the domain of the following functions.
23. f(x) =
1
(x – 2)(x + 6) 24. f (x) =  (x – 2)(x + 6)
21. f(x) =
1
3 – 2x 22. f (x) =  3 – 2x
25. f(x) =
1
x2 – 1 26. f (x) =  1 – x2

93. The Basic Language of Functions
27. –f(3) 28. –g(3) 29. –h(3)
30. 3g(2) 31.2f(2) 32. h(3) + h(0)
33. 2f(4) + 3g(2) 34. f(–3/2) 35. g(1/2)
39. f(3a) 40. g(3a) 41. 3g(a)
42. g(a – b) 43. 2f(a – b)
44. f( )a
1 45. f(a)
1
37. h(–3/2) 38. g(–1/2)36. 1/g(2)
Exercise D. Given the functions f, g and h, find the
outcomes of the following expressions. If it’s not
defined, state so.
f(x) = –2x + 3 g(x) = –x2 + 3x – 2 h(x) =
x + 2
x – 3