More Related Content
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PPTX
What's hot
PDF
(文献紹介)Deep Unrolling: Learned ISTA (LISTA) PDF
PDF
1次式とノルムで構成された最適化問題とその双対問題 PDF
PDF
PDF
PDF
PDF
PDF
科学と機械学習のあいだ:変量の設計・変換・選択・交互作用・線形性 PDF
PPTX
PDF
構造方程式モデルによる因果推論: 因果構造探索に関する最近の発展 PDF
PDF
PDF
PDF
PPTX
PPTX
マルコフ連鎖モンテカルロ法 (2/3はベイズ推定の話) PDF
PPTX
Similar to データ解析4 確率の復習
PDF
PDF
PDF
PPTX
PDF
基礎からのベイズ統計学 輪読会資料 第1章 確率に関するベイズの定理 PPTX
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PPTX
Introduction to Statistical Estimation (統計的推定入門) PDF
演習II.第1章 ベイズ推論の考え方 Part 1.講義ノート PPT
PDF
PPTX
PDF
PRML_titech 2.3.1 - 2.3.7 PDF
More from Hirotaka Hachiya
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
データ解析4 確率の復習
- 1.
- 2.
- 3.
- 4.
確率の定義
7
試行:繰り返すことができて、結果が偶然に決まる実験や観察
事象:試行の結果起こる事柄
標本空間:試行の結果起こりうる全ての事柄の集合
確率の定義:標本空間の大きさを𝑁𝑁、事象𝑥𝑥𝑗𝑗の起こる場合の数
を𝑁𝑁𝑗𝑗とすると、事象𝑥𝑥𝑗𝑗が起こる確率
𝑃𝑃𝑋𝑋 𝑋𝑋 = 𝑥𝑥𝑗𝑗 = 𝑃𝑃𝑋𝑋 𝑥𝑥𝑗𝑗 =
𝑁𝑁𝑗𝑗
𝑁𝑁
𝑋𝑋:確率変数 𝑥𝑥𝑗𝑗:事象(または事象に対応する実現値)
サイコロを振る
2の目が出る
1の目が出る、2の目が出る、…、6の目が出る
𝑃𝑃𝑋𝑋 𝑋𝑋 = 2の目が出る = 𝑃𝑃 𝑋𝑋 = 2 = 1/6
6の目が出る
𝑃𝑃 X :離散確率分布関数
- 5.
確率の例
8
試行:「ボールを箱から取り出す」
事象:「赤のボールが出る」
標本空間:「白のボールが出る」、「赤のボールが出る」
事象「青のボールが出る」の確率:𝑃𝑃𝑋𝑋 𝑥𝑥1 =
𝑁𝑁1
𝑁𝑁
=
6
14
=
3
7
事象「赤のボールが出る」の確率:𝑃𝑃𝑋𝑋 𝑥𝑥2 =
𝑁𝑁2
𝑁𝑁
=
8
14
=
4
7
全ての事象の確率の和は1:𝑃𝑃𝑋𝑋 𝑥𝑥1 + 𝑃𝑃𝑋𝑋 𝑥𝑥2 =
3
7
+
4
7
=1
標本空間𝑆𝑆
確率変数𝑋𝑋(ボールの色)
𝑥𝑥1:青 𝑥𝑥2:赤
6 8
赤の場合の数𝑁𝑁2箱
標本空間𝑆𝑆の大きさ: 𝑁𝑁 = 14
赤の場合の数𝑁𝑁1
- 6.
- 7.
条件付き確率
10
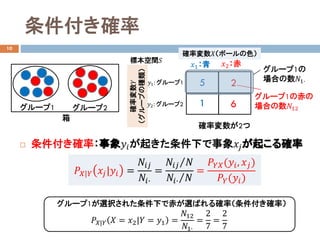
条件付き確率:事象𝑦𝑦𝑖𝑖が起きた条件下で事象𝑥𝑥𝑗𝑗が起こる確率
𝑃𝑃𝑋𝑋|𝑌𝑌 𝑥𝑥𝑗𝑗|𝑦𝑦𝑖𝑖=
𝑁𝑁𝑖𝑖𝑖𝑖
𝑁𝑁𝑖𝑖�
=
⁄𝑁𝑁𝑖𝑖𝑖𝑖 𝑁𝑁
⁄𝑁𝑁𝑖𝑖� 𝑁𝑁
=
𝑃𝑃𝑌𝑌𝑋𝑋(𝑦𝑦𝑖𝑖, 𝑥𝑥𝑗𝑗)
𝑃𝑃𝑌𝑌(𝑦𝑦𝑖𝑖)
標本空間𝑆𝑆
確率変数𝑋𝑋(ボールの色)
確率変数𝑌𝑌
(グループの種類)
𝑥𝑥1:青 𝑥𝑥2:赤
𝑦𝑦1: グループ1 5
1
2
6
箱
グループ1 グループ2
𝑦𝑦2: グループ2
グループ1の赤の
場合の数𝑁𝑁12
グループ1が選択された条件下で赤が選ばれる確率(条件付き確率)
𝑃𝑃𝑋𝑋|𝑌𝑌 𝑋𝑋 = 𝑥𝑥2|𝑌𝑌 = 𝑦𝑦1 =
𝑁𝑁12
𝑁𝑁1�
=
2
7
=
2
7
グループ1の
場合の数𝑁𝑁1�
確率変数が2つ
- 8.
- 9.
乗法定理
12
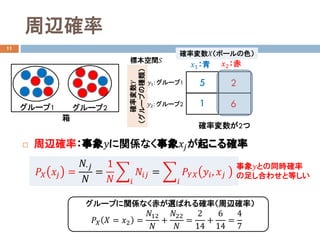
乗法定理:同時確率と条件付き確率との関係
標本空間𝑆𝑆
確率変数𝑋𝑋(ボールの色)
確率変数𝑌𝑌
(グループの種類)
𝑥𝑥1:青 𝑥𝑥2:赤
𝑦𝑦1:グループ1 5
1
2
6
箱
グループ1 グループ2
𝑦𝑦2: グループ2
グループ1の赤が選択される確率
𝑃𝑃𝑌𝑌|𝑋𝑋 𝑌𝑌 = 𝑦𝑦1|𝑋𝑋 = 𝑥𝑥2 =
𝑁𝑁12
𝑁𝑁�2
𝑁𝑁�2
𝑁𝑁
=
2
8
8
14
=
𝑁𝑁12
𝑁𝑁1�
𝑁𝑁1�
𝑁𝑁
=
2
7
7
14
=
1
7
𝑃𝑃𝑌𝑌𝑌𝑌 𝑦𝑦𝑖𝑖, 𝑥𝑥𝑗𝑗 =
𝑁𝑁𝑖𝑖𝑖𝑖
𝑁𝑁
=
𝑁𝑁𝑖𝑖𝑖𝑖
𝑁𝑁�𝑗𝑗
𝑁𝑁�𝑗𝑗
𝑁𝑁
=
𝑁𝑁𝑖𝑖𝑖𝑖
𝑁𝑁𝑖𝑖�
𝑁𝑁𝑖𝑖�
𝑁𝑁
= 𝑃𝑃𝑌𝑌|𝑋𝑋 𝑦𝑦𝑖𝑖 𝑥𝑥𝑗𝑗 𝑃𝑃𝑋𝑋(𝑥𝑥𝑗𝑗) = 𝑃𝑃𝑋𝑋|𝑌𝑌 𝑥𝑥𝑗𝑗 𝑦𝑦𝑖𝑖 𝑃𝑃𝑌𝑌(𝑦𝑦𝑖𝑖)
グループ1の赤の
場合の数𝑁𝑁12
グループ1の
場合の数𝑁𝑁1�
赤の場合の数𝑁𝑁�2
確率変数が2つ
- 10.
ベイズの定理
13
ベイズの定理:乗法定理の展開
事象𝑦𝑦𝑖𝑖を原因、事象𝑥𝑥𝑗𝑗を結果と考える
しかし、実際には診断では、逆の条件付き確率が必要
この結果𝑥𝑥を観測したもとでの原因𝑦𝑦の条件付き確率を
「事後確率」という
𝑃𝑃𝑌𝑌|𝑋𝑋 𝑦𝑦𝑖𝑖|𝑥𝑥𝑗𝑗 =
𝑃𝑃𝑋𝑋𝑋𝑋(𝑥𝑥𝑗𝑗, 𝑦𝑦𝑖𝑖)
𝑃𝑃𝑋𝑋(𝑥𝑥𝑖𝑖)
=
𝑃𝑃𝑋𝑋|𝑌𝑌 𝑥𝑥𝑗𝑗 𝑦𝑦𝑖𝑖 𝑃𝑃𝑌𝑌(𝑦𝑦𝑖𝑖)
𝑃𝑃𝑋𝑋(𝑥𝑥𝑗𝑗)
例えば、原因𝑦𝑦𝑖𝑖:病気、 結果𝑥𝑥𝑗𝑗:血圧140以上とした場合、病気の患者と健康な人
を集めて、血圧140以上の人を観測することにより、以下を求めることができる。
𝑃𝑃𝑋𝑋|𝑌𝑌 𝑋𝑋 = 血圧140以上 Y = 病気 と𝑃𝑃𝑋𝑋|𝑌𝑌 𝑋𝑋 = 血圧140以上 Y = 健康
𝑃𝑃𝑌𝑌|𝑋𝑋 Y = 病気 𝑋𝑋 = 血圧140以上
- 11.
ベイズの定理 続き
14
ベイズの定理:乗法定理の展開
ベイズの定理より、事後確率を求めることができる
ただし、𝑃𝑃(𝑦𝑦𝑗𝑗)を事前確率といい、人間が経験的に決定
分母は、周辺確率と乗法定理より求める
𝑃𝑃𝑌𝑌|𝑋𝑋 𝑦𝑦𝑖𝑖|𝑥𝑥𝑗𝑗 =
𝑃𝑃𝑋𝑋𝑋𝑋(𝑥𝑥𝑗𝑗, 𝑦𝑦𝑖𝑖)
𝑃𝑃𝑋𝑋(𝑥𝑥𝑖𝑖)
=
𝑃𝑃𝑋𝑋|𝑌𝑌 𝑥𝑥𝑗𝑗 𝑦𝑦𝑖𝑖 𝑃𝑃𝑌𝑌(𝑦𝑦𝑖𝑖)
𝑃𝑃𝑋𝑋(𝑥𝑥𝑗𝑗)
事前確率
事後確率
𝑃𝑃𝑌𝑌|𝑋𝑋 Y = 病気 𝑋𝑋 = 血圧140以上 =
𝑃𝑃𝑋𝑋|𝑌𝑌 𝑋𝑋 = 血圧140以上 Y = 病気 𝑃𝑃𝑌𝑌 Y = 病気
𝑃𝑃𝑋𝑋(𝑋𝑋 = 血圧140以上)
例えば、病気の人の割合は、一般的に低いので𝑃𝑃𝑌𝑌 Y = 病気 = 0.1
𝑃𝑃𝑋𝑋 𝑋𝑋 = 血圧140以上 = �
𝑦𝑦∈{病気、健康}
𝑃𝑃𝑋𝑋|𝑌𝑌 𝑋𝑋 = 血圧140以上 Y = 𝑦𝑦 𝑃𝑃𝑌𝑌 Y = 𝑦𝑦
- 12.
- 13.
ベイズの定理の応用例
16
周辺確率より
ベイズの定理より、事後確率𝑃𝑃𝑦𝑦2|𝑥𝑥2 は以下のように求まる。
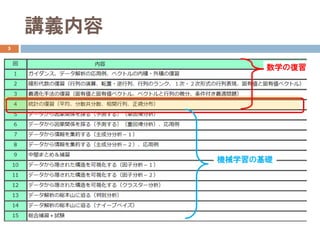
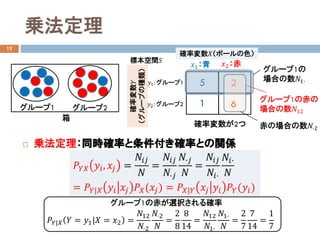
いずれかのグループからボールを1個取り出したと
ころ、 青いボールでした。このボールがグループ2
から取り出された確率𝑃𝑃 𝑦𝑦2|𝑥𝑥2 を求めなさい。
𝑦𝑦𝑖𝑖:グループ𝑖𝑖を選択する事象
𝑥𝑥𝑗𝑗:ボールを取り出す事象(赤:j=1、青:j=2)
𝑃𝑃 𝑥𝑥2 = ∑𝑖𝑖 𝑃𝑃 𝑥𝑥2, 𝑦𝑦𝑖𝑖 = ∑𝑖𝑖 𝑃𝑃 𝑥𝑥2|𝑦𝑦𝑖𝑖 𝑃𝑃 𝑦𝑦𝑖𝑖 =
5
7
1
2
+
1
7
1
2
=
6
14
=
3
7
𝑃𝑃 𝑥𝑥2 𝑦𝑦1 =
5
7
𝑃𝑃 𝑥𝑥2 𝑦𝑦2 =
1
7
𝑃𝑃 𝑦𝑦2|𝑥𝑥2 =
𝑃𝑃 𝑥𝑥2 𝑦𝑦2 𝑃𝑃(𝑦𝑦2)
𝑃𝑃(𝑥𝑥2)
=
1
7
1
2
3
7
=
1
6
グループ1 グループ2
? ?
ただし、各グループを選択した条件下で青いボールを選択する確率は、実験より以下
のようにわかっているとする。また、各グループを選択する事前確率は𝑃𝑃 𝑦𝑦𝑖𝑖 =
1
2
とする
- 14.
- 15.
- 16.
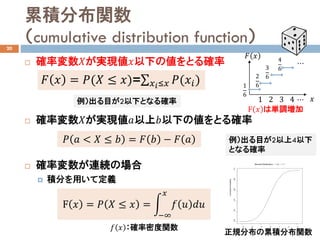
累積分布関数
(cumulative distribution function)20
確率変数𝑋𝑋が実現値𝑥𝑥以下の値をとる確率
確率変数𝑋𝑋が実現値𝑎𝑎以上𝑏𝑏以下の値をとる確率
確率変数が連続の場合
積分を用いて定義
𝐹𝐹 𝑥𝑥 = 𝑃𝑃(𝑋𝑋 ≤ 𝑥𝑥)=∑𝑥𝑥𝑖𝑖≤𝑥𝑥 𝑃𝑃(𝑥𝑥𝑖𝑖)
例)出る目が2以下となる確率
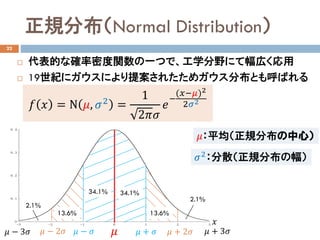
F 𝑥𝑥 = 𝑃𝑃 𝑋𝑋 ≤ 𝑥𝑥 = �
−∞
𝑥𝑥
𝑓𝑓 𝑢𝑢 𝑑𝑑𝑑𝑑
𝑃𝑃 𝑎𝑎 < 𝑋𝑋 ≤ 𝑏𝑏 = 𝐹𝐹 𝑏𝑏 − 𝐹𝐹 𝑎𝑎 例)出る目が2以上4以下
となる確率
𝑓𝑓 𝑥𝑥 :確率密度関数
F 𝑥𝑥 は単調増加
𝑥𝑥
𝐹𝐹 𝑥𝑥
1 2 3 4 ⋯
1
6
2
6
3
6
4
6
⋯
-3 -2 -1 0 1 2 3
0.00.20.40.60.81.0
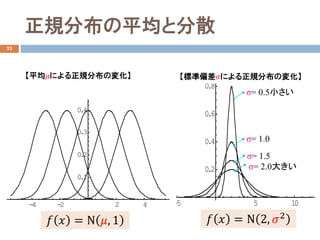
Normal Distribution: = 0, = 1
xCumulativeProbability
正規分布の累積分布関数
- 17.
- 18.
- 19.
- 20.
多変量正規分布
24
多次元の確率変数𝒙𝒙 =𝑥𝑥1, 𝑥𝑥2, … , 𝑥𝑥𝑑𝑑
𝛵𝛵の正規分布
2次元の場合の正規分布
𝑓𝑓 𝒙𝒙 = Ν 𝜇𝜇, 𝜎𝜎2 =
1
2𝜋𝜋
𝑑𝑑
Σ
exp −
1
2
(𝒙𝒙 − 𝝁𝝁)ΤΣ−1(𝒙𝒙 − 𝝁𝝁)
Σ:分散共分散行列
𝝁𝝁 = 𝜇𝜇1, 𝜇𝜇2, … , 𝜇𝜇𝑑𝑑
𝛵𝛵
:平均ベクトル
𝑓𝑓 𝒙𝒙 = Ν 𝜇𝜇, 𝜎𝜎2 =
1
2𝜋𝜋 Σ
exp −
1
2
(𝒙𝒙 − 𝝁𝝁)ΤΣ−1(𝒙𝒙 − 𝝁𝝁)
𝑑𝑑:次元数
- 21.
- 22.
平均値と中央値
26
データの中心を測るための統計量
平均:
データとの二乗誤差和が最小の値:
中央値:データを値の大きさ順に並べたときの真ん中の値
データとの絶対値誤差和が最小の値
𝜇𝜇 = ̅𝑥𝑥 =
1
𝑁𝑁
𝑥𝑥1
+ 𝑥𝑥2
+ ⋯ + 𝑥𝑥 𝑁𝑁
=
1
𝑁𝑁
�
𝑖𝑖=1
𝑁𝑁
𝑥𝑥𝑖𝑖
𝜇𝜇 = min
𝑢𝑢
�
𝑖𝑖=1
𝑁𝑁
𝑥𝑥𝑖𝑖
− 𝑢𝑢
2
二乗差の意味で中心
𝑐𝑐 = min
𝑢𝑢
�
𝑖𝑖=1
𝑁𝑁
𝑥𝑥𝑖𝑖 − 𝑢𝑢
絶対値差の意味で中心
- 23.
平均値と中央値の例
27
データ: 30,10,25, 40,15 の平均と中央値
平均:
中央値
昇順に並べ替える 10, 15,25,30, 40
データ数が5なので、真ん中の3番目の値を選択する
𝜇𝜇 = ̅𝑥𝑥 =
1
5
30 + 10 + 25 + 40 + 15 =24
10, 15,25,30, 40
- 24.
- 25.
分散と共分散
31
分散:1変数のバラツキを測るための統計量
データの平均̅𝑥𝑥からの二乗差の平均:
𝜎𝜎を標準偏差と呼ぶ
共分散: 2変数の相関(直線的な比例関係の強さ)を測るための
統計量
𝑉𝑉𝑉𝑉𝑉𝑉 𝑋𝑋 = 𝜎𝜎2 = S𝒙𝒙𝒙𝒙 =
1
𝑁𝑁
�
𝑖𝑖=1
𝑁𝑁
(𝑥𝑥𝑖𝑖 − ̅𝑥𝑥)2
二乗差の意味でのバラツキ
Cov 𝑋𝑋, 𝑌𝑌 = S𝒙𝒙𝒙𝒙 =
1
𝑁𝑁
∑𝑖𝑖=1
𝑁𝑁
(𝑥𝑥𝑖𝑖
− ̅𝑥𝑥)(𝑦𝑦𝑖𝑖
− �𝑦𝑦)
𝑋𝑋
𝑌𝑌
Cov 𝑋𝑋, 𝑌𝑌 ≫ 0:正の相関
𝑋𝑋
𝑌𝑌
Cov 𝑋𝑋, 𝑌𝑌 ≪ 0:負の相関
𝑋𝑋
𝑌𝑌
Cov 𝑋𝑋, 𝑌𝑌 ≈ 0:無相関
偏差
- 26.
- 27.
- 28.
分散・共分散の行列表現
35
𝒙𝒙 =𝑥𝑥1
, 𝑥𝑥2
, … , 𝑥𝑥 𝑁𝑁 𝚻𝚻
と、𝒚𝒚 = 𝑦𝑦1
, 𝑦𝑦2
, … , 𝑦𝑦 𝑁𝑁 𝚻𝚻
の分散・共分散
分散共分散行列: 2変数の場合2x2の行列
対角成分:それぞれの変数の分散
非対角成分:共分散
𝑺𝑺 =
1
𝑁𝑁
𝑩𝑩𝚻𝚻 𝑩𝑩
=
1
𝑁𝑁
𝒙𝒙 − ̅𝑥𝑥
𝒚𝒚 − �𝑦𝑦
𝒙𝒙 − ̅𝑥𝑥 𝒚𝒚 − �𝑦𝑦
=
1
𝑁𝑁
(𝒙𝒙 − ̅𝑥𝑥)𝚻𝚻(𝒙𝒙 − ̅𝑥𝑥) (𝒙𝒙 − ̅𝑥𝑥)𝚻𝚻(𝒚𝒚 − �𝑦𝑦)
(𝒚𝒚 − �𝑦𝑦)𝚻𝚻
(𝒙𝒙 − ̅𝑥𝑥) (𝒚𝒚 − �𝑦𝑦)𝚻𝚻
(𝒚𝒚 − �𝑦𝑦)
𝑩𝑩 = 𝒙𝒙 − ̅𝑥𝑥 𝒚𝒚 − �𝑦𝑦 =
𝑥𝑥1
− ̅𝑥𝑥
𝑥𝑥2 − ̅𝑥𝑥
⋮
𝑥𝑥 𝑁𝑁 − ̅𝑥𝑥
𝑦𝑦1 − �𝑦𝑦
𝑦𝑦2 − �𝑦𝑦
⋮
𝑦𝑦 𝑁𝑁 − �𝑦𝑦
𝒙𝒙の分散S𝒙𝒙𝒙𝒙
𝒚𝒚の分散S𝒚𝒚𝒚𝒚
𝒙𝒙と𝒚𝒚の共分散S𝒙𝒙𝒙𝒙
N(データ数)×2(変数の数)の行列
- 29.
3変数の分散共分散行列
36
3変数なので3x3の分散共分散行列
対角成分が分散、その他は共分散
𝑩𝑩= 𝒙𝒙 − ̅𝑥𝑥 𝒚𝒚 − �𝑦𝑦 𝒛𝒛 − ̅𝑧𝑧 =
𝑥𝑥1 − ̅𝑥𝑥
𝑥𝑥2
− ̅𝑥𝑥
⋮
𝑥𝑥 𝑁𝑁
− ̅𝑥𝑥
𝑦𝑦1 − �𝑦𝑦
𝑦𝑦2
− �𝑦𝑦
⋮
𝑦𝑦 𝑁𝑁
− �𝑦𝑦
𝑧𝑧1
− ̅𝑧𝑧
𝑧𝑧2
− ̅𝑧𝑧
⋮
𝑧𝑧 𝑁𝑁
− ̅𝑧𝑧
𝑺𝑺 =
1
𝑁𝑁
𝑩𝑩𝚻𝚻 𝑩𝑩
=
1
𝑁𝑁
(𝒙𝒙 − ̅𝑥𝑥)𝚻𝚻(𝒙𝒙 − ̅𝑥𝑥)
(𝒚𝒚 − �𝑦𝑦)𝚻𝚻(𝒙𝒙 − ̅𝑥𝑥)
(𝒛𝒛 − ̅𝑧𝑧)𝚻𝚻(𝒙𝒙 − ̅𝑥𝑥)
(𝒙𝒙 − ̅𝑥𝑥)𝚻𝚻(𝒚𝒚 − �𝑦𝑦)
(𝒚𝒚 − �𝑦𝑦)𝚻𝚻(𝒚𝒚 − �𝑦𝑦)
(𝒛𝒛 − ̅𝑧𝑧)𝚻𝚻(𝒚𝒚 − �𝑦𝑦)
(𝒙𝒙 − ̅𝑥𝑥)𝚻𝚻(𝒛𝒛 − ̅𝑧𝑧)
(𝒚𝒚 − �𝑦𝑦)𝚻𝚻(𝒛𝒛 − ̅𝑧𝑧)
(𝒛𝒛 − ̅𝑧𝑧)𝚻𝚻(𝒛𝒛 − ̅𝑧𝑧)
=
S𝒙𝒙𝒙𝒙 S𝒙𝒙𝒙𝒙 S𝒙𝒙𝒛𝒛
S𝒚𝒚𝒚𝒚 S𝒚𝒚𝒚𝒚 S𝒚𝒚𝒚𝒚
S𝒛𝒛𝒙𝒙 S𝒛𝒛𝒚𝒚 S𝒛𝒛𝒛𝒛
- 30.
- 31.
- 32.
相関係数と相関行列
40
共分散の大きさは、データの値の範囲に依存
異なるデータ間で相関を比較するのが困難
相関係数:共分散を標準偏差で割って正規化
相関行列
𝒓𝒓𝒙𝒙𝒙𝒙 =
S𝒙𝒙𝒚𝒚
S𝒙𝒙𝒙𝒙 S𝒚𝒚𝒚𝒚
=
(𝒙𝒙 − ̅𝑥𝑥)𝚻𝚻(𝒚𝒚 − �𝑦𝑦)
(𝒙𝒙 − ̅𝑥𝑥)𝚻𝚻(𝒙𝒙 − ̅𝑥𝑥) (𝒚𝒚 − �𝑦𝑦)𝚻𝚻(𝒚𝒚 − �𝑦𝑦)
𝑹𝑹 =
𝒓𝒓𝒙𝒙𝒙𝒙 𝒓𝒓𝒙𝒙𝒙𝒙 𝒓𝒓𝒙𝒙𝒛𝒛
𝒓𝒓𝒚𝒚𝒚𝒚 𝒓𝒓𝒚𝒚𝒚𝒚 𝒓𝒓𝒚𝒚𝒚𝒚
𝒓𝒓𝒛𝒛𝒙𝒙 𝒓𝒓𝒛𝒛𝒚𝒚 𝒓𝒓𝒛𝒛𝒛𝒛
𝑺𝑺 =
S𝒙𝒙𝒙𝒙 S𝒙𝒙𝒙𝒙
S𝒚𝒚𝒚𝒚 S𝒚𝒚𝒚𝒚
=
𝟕𝟕𝟒𝟒 𝟔𝟔𝟔𝟔
𝟔𝟔𝟔𝟔 𝟓𝟓𝟓𝟓
【体重xと身長yの分散共分散行列の例】
【体重xと身長yの相関行列の例】
𝑹𝑹 =
𝒓𝒓𝒙𝒙𝒙𝒙 𝒓𝒓𝒙𝒙𝒙𝒙
𝒓𝒓𝒚𝒚𝒚𝒚 𝒓𝒓𝒚𝒚𝒚𝒚
=
𝟏𝟏 𝟎𝟎. 𝟗𝟗𝟗𝟗
𝟎𝟎. 𝟗𝟗𝟗𝟗 𝟏𝟏
- 33.
- 34.
相関係数の解釈
42
データ数の次元のベクトルの内積
𝒙𝒙と𝒚𝒚の相関係数を展開
相関係数はデータ数次元の空間での2つのベクトルのなす角に対応
𝒙𝒙𝒙 = 𝑥𝑥1 − ̅𝑥𝑥, 𝑥𝑥2 − ̅𝑥𝑥, … , 𝑥𝑥 𝑁𝑁 − ̅𝑥𝑥 𝚻𝚻
𝒚𝒚𝒚 = 𝑦𝑦1 − �𝑦𝑦, 𝑦𝑦2 − �𝑦𝑦, … , 𝑦𝑦 𝑁𝑁 − �𝑦𝑦 𝚻𝚻
𝒙𝒙′𝚻𝚻
𝒚𝒚′= 𝒙𝒙𝒙 𝒚𝒚𝒚 cos 𝜃𝜃
𝒙𝒙’
𝒚𝒚𝒚 θ
なす角
𝒓𝒓𝒙𝒙𝒙𝒙 =
(𝒙𝒙 − ̅𝑥𝑥)𝚻𝚻(𝒚𝒚 − �𝑦𝑦)
(𝒙𝒙 − ̅𝑥𝑥)𝚻𝚻(𝒙𝒙 − ̅𝑥𝑥) (𝒚𝒚 − �𝑦𝑦)𝚻𝚻(𝒚𝒚 − �𝑦𝑦)
=
𝒙𝒙𝒙𝚻𝚻 𝒚𝒚𝒚
𝒙𝒙𝒙𝚻𝚻 𝒙𝒙𝒙 𝒚𝒚′𝚻𝚻 𝒚𝒚′
=
𝒙𝒙𝒙 𝒚𝒚𝒚 cos 𝜃𝜃
𝒙𝒙𝒙 𝒚𝒚𝒚
= cos 𝜃𝜃
𝒙𝒙
𝒚𝒚
中程度正の相関
θ = 45° 𝒙𝒙
𝒚𝒚
無相関
θ = 90°
𝒙𝒙𝒚𝒚
強い正の相関
θ = 0° 𝒙𝒙 𝒚𝒚
強い負の相関
θ = 180°
- 35.
- 36.
- 37.
- 38.
- 39.



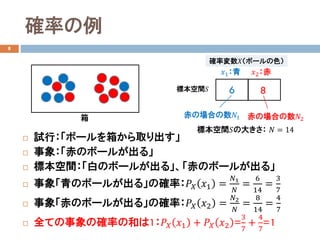










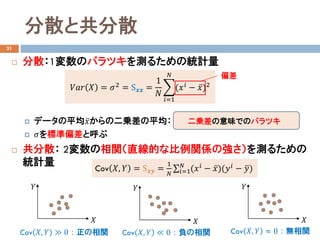
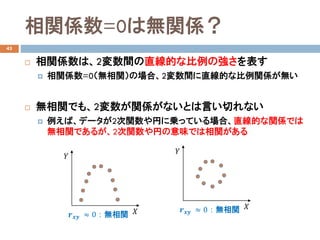
![演習3
32
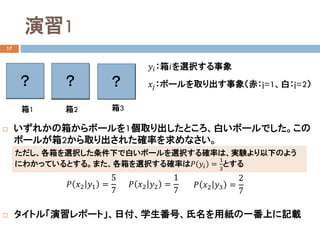
5人の体重と身長のデータ
体重の平均、中央値、分散を求めなさい。
体重と身長の共分散を求めなさい。相関関係を述べなさい。
タイトル「演習レポート」、日付、学生番号、氏名を用紙の一
番上に記載
体重𝑋𝑋 [kg] 身長𝑌𝑌[cm]
50 160
45 155
60 170
70 175
55 165](https://image.slidesharecdn.com/dataanalysis4probability-181114031255/85/4-26-320.jpg)

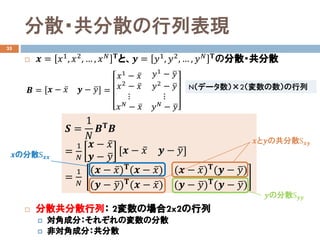

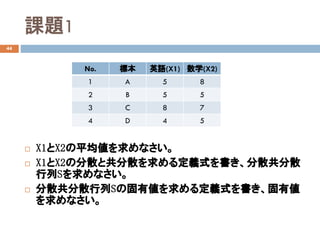
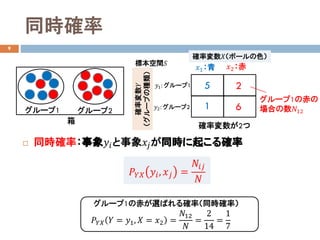
![演習4
37
5人の体重と身長のデータ
体重と身長の分散共分散行列を求めなさい。
タイトル「演習レポート」、日付、学生番号、氏名を用紙の一
番上に記載
体重𝑋𝑋 [kg] 身長𝑌𝑌[cm]
50 160
45 155
60 170
70 175
55 165](https://image.slidesharecdn.com/dataanalysis4probability-181114031255/85/4-30-320.jpg)