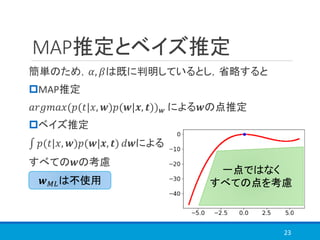
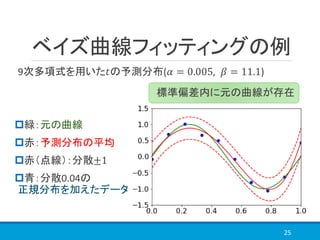
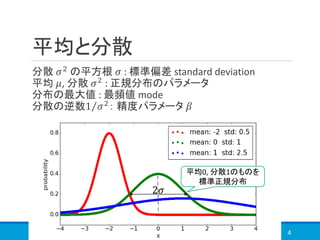
i.i.d. の変数の生成と混合分布を用いて,最尤推定しているところなど一部参考文献とニュアンスが異なっているかと思います。
見やすいと思った資料↓↓
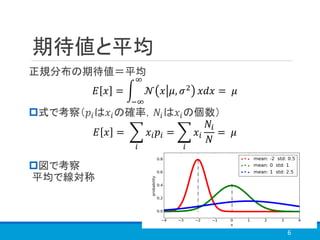
1章
https://speakerdeck.com/tkngue/prml-chapter01-at-nut
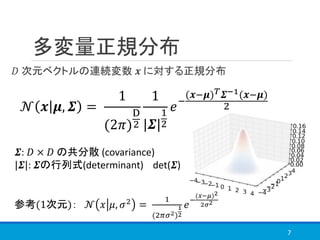
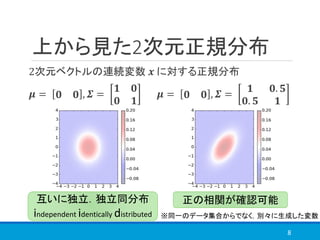
3章
http://www.iip.ist.i.kyoto-u.ac.jp/member/keisuke/resources/PRML_sec3_2.pdf
https://www.slideshare.net/yasunoriozaki12/prml-29439402
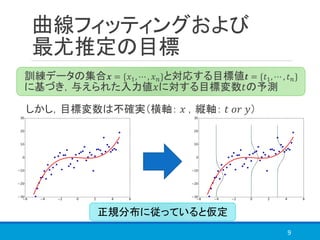
5章前半(特にわかりやすいかと)
https://www.slideshare.net/t_koshikawa/prml-5-pp227pp247







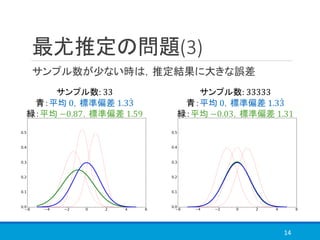
![最尤推定の問題(2)
数学的な問題としては,解の自由度が減少
図でわかる問題としては
3つの分布から得られる混合分布を考えると,
赤:平均[−1,0,1],標準偏差 1
青:平均 0,標準偏差 1.3 ሶ3
13
サンプル数が十分な時
青(理想)の分布に
⇒ では,少ない時は?](https://image.slidesharecdn.com/prml1-181201181045/85/PRML-1-2-4-1-2-6-13-320.jpg)