Download as PDF, PPTX
![[DL輪読会]Understanding Black-box Predictions via Influence Functions](https://cdn.slidesharecdn.com/ss_thumbnails/dlhacksinffunc-170822055634-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]Deep Learning 第5章 機械学習の基礎](https://cdn.slidesharecdn.com/ss_thumbnails/deeplearning5-180601021956-thumbnail.jpg?width=640&height=640&fit=bounds)
データ解析5 単回帰分析
- 1.
- 2.
- 3. 機械学習手法の種類 9 問題（データの条件など）と目的に合わせて適切な 機械学習方法を選択する必要がある 問題 定義代表的な方法 応用例 教師あり学習 入力と出力のデータに基づき、 入力を出力に変換する関数を 学習 SVM, 回帰、決定木、 ランダムフォーレス トなど スパム分類、顔検出、一 般物体認識、将棋局面 の評価など 教師なし学習 入力のみの事例に基づき、 入力の特性 （パターン、構造） を学習 PCA, LDA、HMMなど データの可視化 （クラスタリング、次元圧 縮） 半教師学習 入力のうち部分的に付与された 出力の事例に基づき 入力を出力に変換する関数を 学習 transductiveSVM, Laplacian SVMなど 画像、音声、Webログな どの大量データで、コス トの問題で一部のデータ のみしか出力（答え）が 付与されていない場合 強化学習 入力と、出力に対する報酬 （評価）のデータに基づき、 入力を出力に変換する関数を 学習 Q-learning、policy iteration, policy gradient ロボット制御、Web広告 選択、マーケティング
- 4. 回帰分析とは 10 入力と出力の組のデータから、入力に対する出力を予測 する関係モデルを学習 入力：説明変数 スカラー（１変数）の場合：単回帰分析 ベクトル（多変数）の場合：重回帰分析 出力：目的変数 実数スカラー 出力𝑦𝑦 ：収穫量 肥料の種類と量 雨量 入力𝑥𝑥 日照時間 関係モデルによる予測
- 5. 単回帰分析の例 11 人口とゴミ排出量のデータから、将来のゴミ排出量を予測 ゴミ排出量＝傾き Ｘ人口 ＋ 切片 ＋ 残差 （説明変数） 100000 300000 50000 100000 150000 500000 人口 ゴ ミ 排 出 量 傾き 切片 予測 残差 直線 （目的変数）
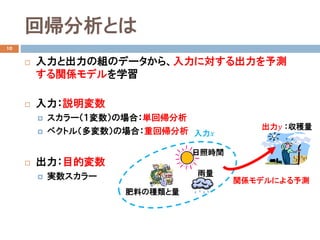
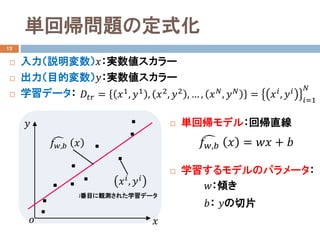
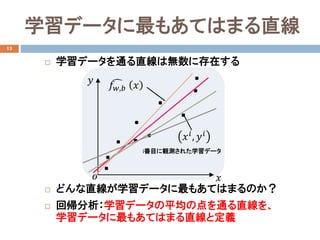
- 6. 単回帰問題の定式化 入力（説明変数）𝑥𝑥：実数値スカラー 出力（目的変数）𝑦𝑦：実数値スカラー 学習データ： 単回帰モデル：回帰直線 学習するモデルのパラメータ： 12 𝐷𝐷𝑡𝑡𝑡𝑡 = 𝑥𝑥1 , 𝑦𝑦1 , 𝑥𝑥2 , 𝑦𝑦2 , … , 𝑥𝑥 𝑁𝑁 , 𝑦𝑦 𝑁𝑁 = 𝑥𝑥𝑖𝑖 , 𝑦𝑦𝑖𝑖 𝑖𝑖=1 𝑁𝑁 𝑤𝑤：傾き 𝑏𝑏： 𝑦𝑦の切片 �𝑓𝑓𝑤𝑤,𝑏𝑏 𝑥𝑥 = 𝑤𝑤𝑤𝑤 + 𝑏𝑏 𝑥𝑥 𝑦𝑦 𝑜𝑜 i番目に観測された学習データ 𝑥𝑥𝑖𝑖, 𝑦𝑦𝑖𝑖 �𝑓𝑓𝑤𝑤,𝑏𝑏 𝑥𝑥
- 7. 学習データに最もあてはまる直線 13 学習データを通る直線は無数に存在する どんな直線が学習データに最もあてはまるのか？ 回帰分析：学習データの平均の点を通る直線を、 学習データに最もあてはまる直線と定義 𝑥𝑥 𝑦𝑦 𝑜𝑜 i番目に観測された学習データ 𝑥𝑥𝑖𝑖 , 𝑦𝑦𝑖𝑖 �𝑓𝑓𝑤𝑤,𝑏𝑏 𝑥𝑥
- 8. Y軸成分の平均誤差の最小化 14 説明変数𝑥𝑥は正確と仮定した場合、目的変数𝑦𝑦のみを 予測するので、学習データの𝑦𝑦成分の平均を考える モデル�𝑓𝑓𝑤𝑤,𝑏𝑏 𝑥𝑥 と学習データの𝑦𝑦成分の二乗誤差和を最小化 𝜇𝜇 = 1 𝑁𝑁 � 𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖 = min 𝑤𝑤,𝑏𝑏 � 𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖 − �𝑓𝑓𝑤𝑤,𝑏𝑏 𝑥𝑥 2 𝜀𝜀𝑖𝑖 平均は二乗誤差和の最小と等しい 𝑦𝑦 𝑜𝑜 i番目に観測された学習データ 𝑥𝑥𝑖𝑖, 𝑦𝑦𝑖𝑖 𝑥𝑥 �𝑓𝑓𝑤𝑤,𝑏𝑏 𝑥𝑥 誤差𝜀𝜀𝑖𝑖 最小二乗法
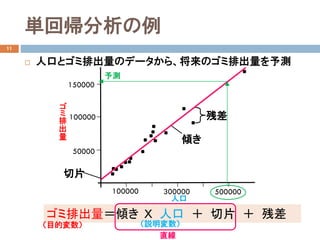
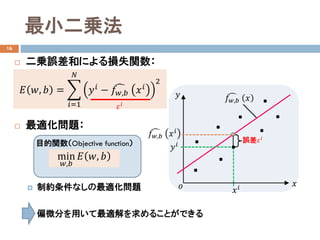
- 9. 最小二乗法 16 二乗誤差和による損失関数： 最適化問題： 制約条件なしの最適化問題 偏微分を用いて最適解を求めることができる 𝐸𝐸 𝑤𝑤, 𝑏𝑏 = � 𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖 − �𝑓𝑓𝑤𝑤,𝑏𝑏 𝑥𝑥𝑖𝑖 2 𝑥𝑥 𝑦𝑦 𝑜𝑜 誤差𝜀𝜀𝑖𝑖 �𝑓𝑓𝑤𝑤,𝑏𝑏 𝑥𝑥 𝑥𝑥𝑖𝑖 𝑦𝑦𝑖𝑖 �𝑓𝑓𝑤𝑤,𝑏𝑏 𝑥𝑥𝑖𝑖 目的関数（Objective function） min 𝑤𝑤,𝑏𝑏 𝐸𝐸 𝑤𝑤, 𝑏𝑏 𝜀𝜀𝑖𝑖
- 10. 二乗誤差和による損失関数を展開 𝑤𝑤について偏微分し0とおく 𝑏𝑏について偏微分し0とおく ①と②から 最小二乗法によるパラメータ最適化 17 𝐸𝐸 𝑤𝑤, 𝑏𝑏 = ∑𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖 − �𝑓𝑓𝑤𝑤,𝑏𝑏 𝑥𝑥𝑖𝑖 2 = ∑𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖2 − 2𝑦𝑦𝑖𝑖 𝑤𝑤𝑥𝑥𝑖𝑖 + 𝑏𝑏 + 𝑤𝑤𝑥𝑥𝑖𝑖 + 𝑏𝑏 2 𝜕𝜕𝐸𝐸(𝑤𝑤,𝑏𝑏) 𝜕𝜕𝑤𝑤 = ∑𝑖𝑖=1 𝑁𝑁 −2𝑦𝑦𝑖𝑖 𝑥𝑥𝑖𝑖 + 2 𝑤𝑤𝑥𝑥𝑖𝑖 + 𝑏𝑏 𝑥𝑥𝑖𝑖 = − ∑𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖 𝑥𝑥𝑖𝑖+ ∑𝑖𝑖=1 𝑁𝑁 𝑤𝑤𝑥𝑥𝑖𝑖2 + ∑𝑖𝑖=1 𝑁𝑁 𝑏𝑏𝑥𝑥𝑖𝑖 = 0 �𝑓𝑓𝑤𝑤,𝑏𝑏 𝑥𝑥 = 𝑤𝑤𝑤𝑤 + 𝑏𝑏 𝜕𝜕𝐸𝐸(𝑤𝑤,𝑏𝑏) 𝜕𝜕𝑏𝑏 = ∑𝑖𝑖=1 𝑁𝑁 −2𝑦𝑦𝑖𝑖 + 2 𝑤𝑤𝑥𝑥𝑖𝑖 + 𝑏𝑏 = − ∑𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖 + ∑𝑖𝑖=1 𝑁𝑁 𝑤𝑤𝑥𝑥𝑖𝑖 + 𝑁𝑁𝑁𝑁 = 0 ―① ―② 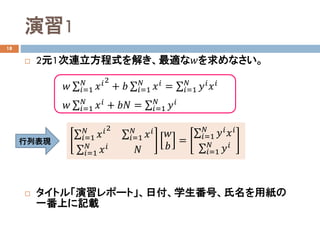𝑤𝑤 ∑𝑖𝑖=1 𝑁𝑁 𝑥𝑥𝑖𝑖2 + 𝑏𝑏 ∑𝑖𝑖=1 𝑁𝑁 𝑥𝑥𝑖𝑖 = ∑𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖 𝑥𝑥𝑖𝑖 𝑤𝑤 ∑𝑖𝑖=1 𝑁𝑁 𝑥𝑥𝑖𝑖 + 𝑏𝑏𝑏𝑏 = ∑𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖 2元1次連立方程式 ∑𝑖𝑖=1 𝑁𝑁 𝑏𝑏 = 𝑁𝑁
- 11. 演習1 18 2元1次連立方程式を解き、最適な𝑤𝑤を求めなさい。 タイトル「演習レポート」、日付、学生番号、氏名を用紙の 一番上に記載 𝑤𝑤∑𝑖𝑖=1 𝑁𝑁 𝑥𝑥𝑖𝑖2 + 𝑏𝑏 ∑𝑖𝑖=1 𝑁𝑁 𝑥𝑥𝑖𝑖 = ∑𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖 𝑥𝑥𝑖𝑖 𝑤𝑤 ∑𝑖𝑖=1 𝑁𝑁 𝑥𝑥𝑖𝑖 + 𝑏𝑏𝑏𝑏 = ∑𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖 ∑𝑖𝑖=1 𝑁𝑁 𝑥𝑥𝑖𝑖2 ∑𝑖𝑖=1 𝑁𝑁 𝑥𝑥𝑖𝑖 ∑𝑖𝑖=1 𝑁𝑁 𝑥𝑥𝑖𝑖 𝑁𝑁 𝑤𝑤 𝑏𝑏 = ∑𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖 𝑥𝑥𝑖𝑖 ∑𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖行列表現
- 12. 演習2 20 1. 分散S𝒙𝒙𝒙𝒙と共分散S𝒙𝒙𝒙𝒙の定義から最適な傾き𝑤𝑤∗が、 以下のように簡単化できることを証明しなさい。 2. 𝑤𝑤∗ を以下の式に代入し、切片𝑏𝑏の最適解を求めなさい。 分散S𝒙𝒙𝒙𝒙と共分散S𝒙𝒙𝒙𝒙の定義 タイトル「演習レポート」、日付、学生番号、氏名を用紙の一 番上に記載 𝑤𝑤∗ = 𝑁𝑁 ∑𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖 𝑥𝑥𝑖𝑖−∑𝑖𝑖=1 𝑁𝑁 𝑥𝑥𝑖𝑖 ∑𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖 𝑁𝑁 ∑𝑖𝑖=1 𝑁𝑁 𝑥𝑥𝑖𝑖2 − ∑𝑖𝑖=1 𝑁𝑁 𝑥𝑥𝑖𝑖 2 = S𝒙𝒙𝒙𝒙 S𝒙𝒙𝒙𝒙 S𝒙𝒙𝒙𝒙 = 1 𝑁𝑁 � 𝑖𝑖=1 𝑁𝑁 (𝑥𝑥𝑖𝑖 − ̅𝑥𝑥)2 S𝒙𝒙𝒙𝒙 = 1 𝑁𝑁 � 𝑖𝑖=1 𝑁𝑁 (𝑥𝑥𝑖𝑖 − ̅𝑥𝑥)(𝑦𝑦𝑖𝑖 − �𝑦𝑦) 𝜕𝜕𝐸𝐸(𝑤𝑤,𝑏𝑏) 𝜕𝜕𝑏𝑏 = ∑𝑖𝑖=1 𝑁𝑁 −2𝑦𝑦𝑖𝑖 + 2 𝑤𝑤𝑥𝑥𝑖𝑖 + 𝑏𝑏 = − ∑𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖+ ∑𝑖𝑖=1 𝑁𝑁 𝑤𝑤𝑥𝑥𝑖𝑖 + 𝑁𝑁𝑁𝑁 = 0 ―②
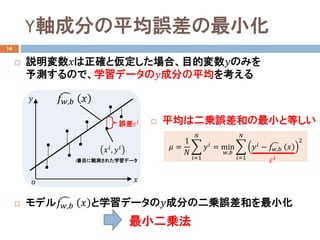
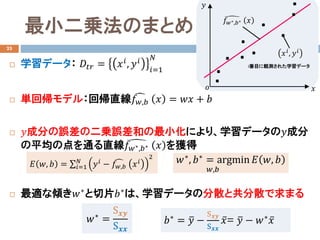
- 13. 最小二乗法のまとめ 学習データ： 𝐷𝐷𝑡𝑡𝑡𝑡= 𝑥𝑥𝑖𝑖, 𝑦𝑦𝑖𝑖 𝑖𝑖=1 𝑁𝑁 単回帰モデル：回帰直線 �𝑓𝑓𝑤𝑤,𝑏𝑏 𝑥𝑥 = 𝑤𝑤𝑤𝑤 + 𝑏𝑏 𝑦𝑦成分の誤差の二乗誤差和の最小化により、学習データの𝑦𝑦成分 の平均の点を通る直線 �𝑓𝑓𝑤𝑤∗,𝑏𝑏∗ 𝑥𝑥 を獲得 最適な傾き𝑤𝑤∗と切片𝑏𝑏∗は、学習データの分散と共分散で求まる 23 i番目に観測された学習データ 𝑥𝑥𝑖𝑖 , 𝑦𝑦𝑖𝑖 �𝑓𝑓𝑤𝑤∗,𝑏𝑏∗ 𝑥𝑥 𝑥𝑥 𝑦𝑦 𝑜𝑜 𝐸𝐸 𝑤𝑤, 𝑏𝑏 = ∑𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖 − �𝑓𝑓𝑤𝑤,𝑏𝑏 𝑥𝑥𝑖𝑖 2 𝑤𝑤∗, 𝑏𝑏∗ = argmin 𝑤𝑤,𝑏𝑏 𝐸𝐸 𝑤𝑤, 𝑏𝑏 𝑏𝑏∗ = �𝑦𝑦 − S𝒙𝒙𝒙𝒙 S𝒙𝒙𝒙𝒙 ̅𝑥𝑥= �𝑦𝑦 − 𝑤𝑤∗ ̅𝑥𝑥𝑤𝑤∗ = S𝒙𝒙𝒙𝒙 S𝒙𝒙𝒙𝒙
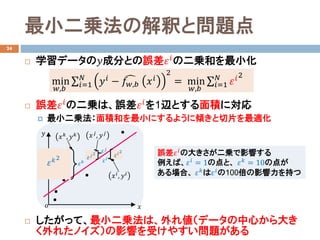
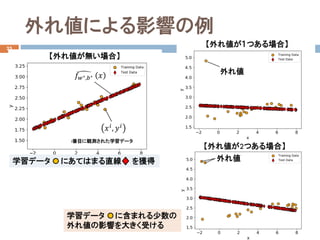
- 14. 最小二乗法の解釈と問題点 24 学習データの𝑦𝑦成分との誤差𝜀𝜀𝑖𝑖の二乗和を最小化 誤差𝜀𝜀𝑖𝑖の二乗は、誤差𝜀𝜀𝑖𝑖を1辺とする面積に対応 最小二乗法：面積和を最小にするように傾きと切片を最適化 したがって、最小二乗法は、外れ値（データの中心から大き く外れたノイズ）の影響を受けやすい問題がある min 𝑤𝑤,𝑏𝑏 ∑𝑖𝑖=1 𝑁𝑁 𝑦𝑦𝑖𝑖 − �𝑓𝑓𝑤𝑤,𝑏𝑏 𝑥𝑥𝑖𝑖 2 = min 𝑤𝑤,𝑏𝑏 ∑𝑖𝑖=1 𝑁𝑁 𝜀𝜀𝑖𝑖2 誤差𝜀𝜀𝑖𝑖の大きさが二乗で影響する 例えば、𝜀𝜀𝑖𝑖 = 1の点と、 𝜀𝜀 𝑘𝑘 = 10の点が ある場合、 𝜀𝜀 𝑘𝑘 は𝜀𝜀𝑖𝑖 の100倍の影響力を持つ𝑥𝑥𝑖𝑖 , 𝑦𝑦𝑖𝑖 𝑥𝑥 𝑦𝑦 𝑜𝑜 𝑥𝑥 𝑘𝑘 , 𝑦𝑦 𝑘𝑘 𝑥𝑥 𝑗𝑗 , 𝑦𝑦 𝑗𝑗 𝜀𝜀 𝑘𝑘 𝜀𝜀𝑖𝑖 𝜀𝜀 𝑘𝑘2 𝜀𝜀𝑖𝑖2𝜀𝜀 𝑗𝑗 𝜀𝜀 𝑗𝑗2
- 15. 外れ値による影響の例 25 【外れ値が無い場合】 学習データ にあてはまる直線 を獲得 外れ値 【外れ値が１つある場合】 �𝑓𝑓𝑤𝑤∗,𝑏𝑏∗𝑥𝑥 i番目に観測された学習データ 𝑥𝑥𝑖𝑖 , 𝑦𝑦𝑖𝑖 【外れ値が2つある場合】 外れ値 学習データ に含まれる少数の 外れ値の影響を大きく受ける
- 16. 演習3 26 タイトル「演習レポート」、日付、学生番号、氏名を用紙の一 番上に記載 表１ 販売台数とＣＭ総時間 月間ＣＭ総時間 販売台数 (x) (y) . 1 23 76 2 24 77 3 29 82 4 27 84 5 23 74 6 24 81 7 27 86 8 26 79 9 21 77 10 31 82 1. 表1の単回帰直線を求めなさい。 2. 11月のＣＭ総時間数が30の場合、 販売台数の予測値を求めなさい。
- 17. 課題1 28 表に基づき、変数Xを用いて変数Yを予測する回帰直線を 求めなさい。 1 23 4 5 6 7 8 9 10 X 2.8 3.4 3.6 5.8 7.0 9.5 10.2 12.3 13.2 13.4 Y 0.6 3.0 0.4 1.5 15.0 13.4 7.6 19.8 18.3 18.9
- 18. レポートの提出方法 29 演習レポート： タイトル「演習レポート」、日付・学生番号・氏名を用紙の一番上に記載 課題レポート ： タイトル「課題レポート」、出題日・学生番号・氏名を用紙の一番上に記載 2ページ以上になる場合は、ホッチキス留め A4サイズの用紙を使用 一度に複数の課題レポートを提出する場合出題日ごとに別々に綴じる