More Related Content
What's hot
What's hot (20)
Similar to データ解析13 線形判別分析
Similar to データ解析13 線形判別分析 (20)
More from Hirotaka Hachiya
データ解析13 線形判別分析
- 1. データ解析 第13回 2018年7月12日 八谷 大岳 1
- 3. 内容： 7 判別分析とは 線形判別分析の基礎 直線を用いたカテゴリ判別 カテゴリ間分散・カテゴリ内分散による定式化 直線の最適化 線形判別分析の応用 手順 Pythonによる実装例
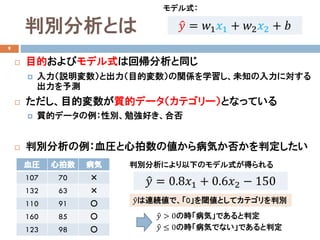
- 4. 回帰分析の復習 8 回帰分析の目的：入力（説明変数）と出力（目的変数）の 関係を学習し、未知の入力に対する出力を予測する 目的変数：量的なデータ（連続値） 例：靴サイズ、ゴミの排出量、身長、株価、家賃など �𝑦𝑦 = 𝑤𝑤1 𝑥𝑥1 + 𝑤𝑤2 𝑥𝑥2 + 𝑏𝑏モデル式： 身長(x１) 体重(ｘ２) 靴サイズ(y) 162 44 24.0 165 48 24.5 168 53 25.5 160 45 22.5 158 45 23.0 153 43 22.0 158 45 23.0 168 50 24.0 157 52 23.0 154 42 23.0 170 48 25.0 157 45 23.5 (cm) (kg) (cm) 説明変数𝑥𝑥1 説明変数𝑥𝑥2 目的変数𝑦𝑦 目的変数𝑦𝑦 靴サイズ＝傾き Ｘ 身長 ＋ 傾き Ｘ 体重 ＋ 切片 ＋ 残差 𝑤𝑤1 説明変数𝑥𝑥1 説明変数𝑥𝑥2𝑤𝑤2 𝑏𝑏 𝜀𝜀 モデルパラメータ： 𝑤𝑤1、𝑤𝑤2（傾き）、𝑏𝑏（𝑦𝑦の切片）
- 5. 判別分析とは 9 目的およびモデル式は回帰分析と同じ 入力（説明変数）と出力（目的変数）の関係を学習し、未知の入力に対する 出力を予測 ただし、目的変数が質的データ（カテゴリー）となっている 質的データの例：性別、勉強好き、合否 判別分析の例：血圧と心拍数の値から病気か否かを判定したい 血圧 心拍数 病気 107 70 × 132 63 × 110 91 〇 160 85 〇 123 98 〇 �𝑦𝑦 = 𝑤𝑤1 𝑥𝑥1 + 𝑤𝑤2 𝑥𝑥2 + 𝑏𝑏 モデル式： �𝑦𝑦 = 0.8𝑥𝑥1 + 0.6𝑥𝑥2 − 150 判別分析により以下のモデル式が得られる �𝑦𝑦 > 0の時「病気」であると判定 �𝑦𝑦 ≤ 0の時「病気でない」であると判定 �𝑦𝑦は連続値で、「0」を閾値としてカテゴリを判別
- 6. 演習1 10 1. 以下のデータ分析手法の概要について述べなさい。 2. 以下のモデル式が与えられた時、 入力「血圧𝑥𝑥1 = 154」と 「心拍数𝑥𝑥2 = 75」 が病気か否かを判別しなさい タイトル「演習レポート」、日付、学生番号、氏名を用紙の一番上 に記載 分析手法 概要 回帰分析 判別分析 �𝑦𝑦 = 0.8𝑥𝑥1 + 0.6𝑥𝑥2 − 150 �𝑦𝑦 > 0の時「病気」であると判定 �𝑦𝑦 ≤ 0の時「病気でない」であると判定
- 7. 内容： 12 判別分析とは 線形判別分析の基礎 直線を用いたカテゴリ判別 カテゴリ間分散・カテゴリ内分散による定式化 直線の最適化 線形判別分析の応用 手順 Pythonによる実装例
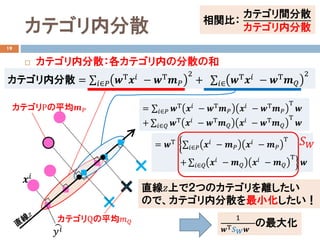
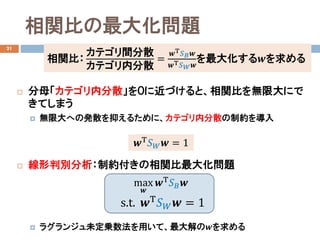
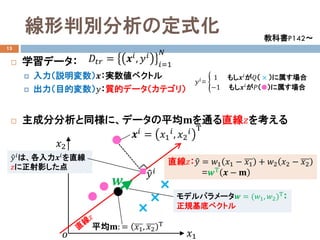
- 8. 線形判別分析の定式化 13 学習データ： 入力（説明変数）𝒙𝒙：実数値ベクトル 出力（目的変数）𝑦𝑦：質的データ（カテゴリ） 主成分分析と同様に、データの平均𝐦𝐦を通る直線𝑧𝑧を考える 𝐷𝐷𝑡𝑡𝑡𝑡 = 𝒙𝒙𝑖𝑖, 𝑦𝑦𝑖𝑖 𝑖𝑖=1 𝑁𝑁 𝑜𝑜 𝑥𝑥1 𝑥𝑥2 教科書P142～ 直線𝑧𝑧：�𝑦𝑦 = 𝑤𝑤1 𝑥𝑥1 − 𝑥𝑥1 + 𝑤𝑤2 𝑥𝑥2 − 𝑥𝑥2 =𝒘𝒘Τ 𝒙𝒙 − 𝐦𝐦 𝒙𝒙𝑖𝑖 = 𝑥𝑥1 𝑖𝑖 , 𝑥𝑥2 𝑖𝑖 Τ �𝑦𝑦𝑖𝑖 モデルパラメータ𝒘𝒘 = (𝑤𝑤1, 𝑤𝑤2)Τ： 正規基底ベクトル �𝑦𝑦𝑖𝑖は、各入力𝒙𝒙𝑖𝑖を直線 𝑧𝑧に正射影した点 平均𝐦𝐦: = 𝑥𝑥1, 𝑥𝑥2 Τ 𝒘𝒘 𝑦𝑦𝑖𝑖 = � 1 もし𝒙𝒙𝑖𝑖 が𝑄𝑄（ × ）に属す場合 −1 もし𝒙𝒙𝑖𝑖 が𝑃𝑃（●）に属す場合
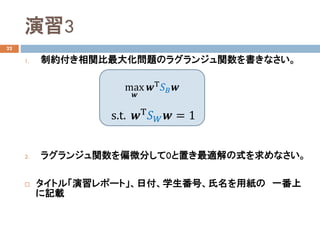
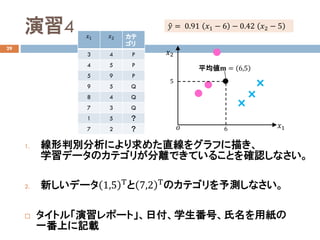
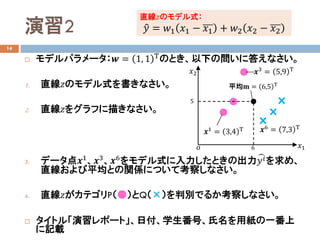
- 9. 演習2 14 モデルパラメータ：𝒘𝒘 = 1, 1 Τ のとき、以下の問いに答えなさい。 1. 直線𝑧𝑧のモデル式を書きなさい。 2. 直線𝑧𝑧をグラフに描きなさい。 3. データ点𝒙𝒙1 、𝒙𝒙3 、𝒙𝒙6 をモデル式に入力したときの出力 �𝑦𝑦𝑖𝑖を求め、 直線および平均との関係について考察しなさい。 4. 直線𝑧𝑧がカテゴリP（●）とQ（×）を判別でるか考察しなさい。 タイトル「演習レポート」、日付、学生番号、氏名を用紙の一番上 に記載 6𝑜𝑜 𝑥𝑥1 𝑥𝑥2 5 平均𝐦𝐦 = 6,5 Τ 𝒙𝒙3 = 5,9 Τ 𝒙𝒙6 = 7,3 Τ 𝒙𝒙1 = 3,4 Τ 直線𝑧𝑧のモデル式： �𝑦𝑦 = 𝑤𝑤1 𝑥𝑥1 − 𝑥𝑥1 + 𝑤𝑤2 𝑥𝑥2 − 𝑥𝑥2
- 10. 内容： 17 判別分析とは 線形判別分析の基礎 直線を用いたカテゴリ判別 カテゴリ間分散・カテゴリ内分散による定式化 直線の最適化 線形判別分析の応用 手順 Pythonによる実装例
- 11. カテゴリ間分散 18 カテゴリ（PとQ）を分離する直線𝑧𝑧を求めたい 線形判別分析：相関比を最大化する直線𝑧𝑧を求める 相関比： カテゴリ間分散 カテゴリ内分散 カテゴリ間分散：カテゴリ中心間の分散（距離） カテゴリ間分散 = 𝒘𝒘Τ 𝒎𝒎𝑃𝑃 − 𝒘𝒘Τ 𝒎𝒎𝑄𝑄 2 = 𝒘𝒘Τ 𝒎𝒎𝑃𝑃 − 𝒎𝒎𝑄𝑄 2 = 𝒘𝒘Τ 𝒎𝒎𝑃𝑃 − 𝒎𝒎𝑄𝑄 𝒎𝒎𝑃𝑃 − 𝒎𝒎𝑄𝑄 Τ 𝒘𝒘 カテゴリPの平均𝒎𝒎𝑃𝑃 直線𝑧𝑧上で２つのカテゴリを離したいので、 カテゴリ間分散を最大化したい！ 𝑆𝑆𝐵𝐵 カテゴリQの平均𝒎𝒎𝑄𝑄 𝒘𝒘Τ 𝒎𝒎𝑃𝑃 𝒘𝒘Τ 𝒎𝒎𝑄𝑄
- 12. カテゴリ内分散 19 カテゴリ内分散：各カテゴリ内の分散の和 相関比： カテゴリ間分散 カテゴリ内分散 カテゴリPの平均𝒎𝒎𝑃𝑃 �𝑦𝑦𝑖𝑖 カテゴリ内分散 = ∑𝑖𝑖∈𝑃𝑃 𝒘𝒘Τ 𝒙𝒙𝑖𝑖 − 𝒘𝒘Τ 𝒎𝒎𝑃𝑃 2 + ∑𝑖𝑖∈ 𝒘𝒘Τ 𝒙𝒙𝑖𝑖 − 𝒘𝒘Τ 𝒎𝒎𝑄𝑄 2 = ∑𝑖𝑖∈𝑃𝑃 𝒘𝒘Τ 𝒙𝒙𝑖𝑖 − 𝒘𝒘Τ 𝒎𝒎𝑃𝑃 𝒙𝒙𝑖𝑖 − 𝒘𝒘Τ 𝒎𝒎𝑃𝑃 Τ 𝒘𝒘 + ∑𝑖𝑖∈𝑄𝑄 𝒘𝒘Τ 𝒙𝒙𝑖𝑖 − 𝒘𝒘Τ 𝒎𝒎𝑄𝑄 𝒙𝒙𝑖𝑖 − 𝒘𝒘Τ 𝒎𝒎𝑄𝑄 Τ 𝒘𝒘 = 𝒘𝒘Τ �∑𝑖𝑖∈𝑃𝑃 𝒙𝒙𝑖𝑖 − 𝒎𝒎𝑃𝑃 𝒙𝒙𝑖𝑖 − 𝒎𝒎𝑃𝑃 Τ �+ ∑𝑖𝑖∈𝑄𝑄 𝒙𝒙𝑖𝑖 − 𝒎𝒎𝑄𝑄 𝒙𝒙𝑖𝑖 − 𝒎𝒎𝑄𝑄 Τ 𝒘𝒘 𝑆𝑆𝑊𝑊 直線𝑧𝑧上で２つのカテゴリを離したい ので、カテゴリ内分散を最小化したい！ 𝒙𝒙𝑖𝑖 カテゴリQの平均𝑚𝑚𝑄𝑄 1 𝒘𝒘Τ 𝑆𝑆 𝑊𝑊 𝒘𝒘 の最大化
- 13. 内容： 20 判別分析とは 線形判別分析の基礎 直線を用いたカテゴリ判別 カテゴリ間分散・カテゴリ内分散による定式化 直線の最適化 線形判別分析の応用 手順 Pythonによる実装例
- 14. 相関比の最大化問題 21 分母「カテゴリ内分散」を０に近づけると、相関比を無限大にで きてしまう 無限大への発散を抑えるために、カテゴリ内分散の制約を導入 線形判別分析：制約付きの相関比最大化問題 ラグランジュ未定乗数法を用いて、最大解の𝒘𝒘を求める max 𝒘𝒘 𝒘𝒘Τ 𝑆𝑆𝐵𝐵 𝒘𝒘 s.t. 𝒘𝒘Τ 𝑆𝑆𝑊𝑊 𝒘𝒘 = 1 𝒘𝒘Τ 𝑆𝑆𝑊𝑊 𝒘𝒘 = 1 相関比： カテゴリ間分散 カテゴリ内分散 = 𝒘𝒘Τ 𝑆𝑆𝐵𝐵 𝒘𝒘 𝒘𝒘Τ 𝑆𝑆 𝑊𝑊 𝒘𝒘 を最大化する𝒘𝒘を求める
- 15. 演習3 22 1. 制約付き相関比最大化問題のラグランジュ関数を書きなさい。 2. ラグランジュ関数を偏微分して0と置き最適解の式を求めなさい。 タイトル「演習レポート」、日付、学生番号、氏名を用紙の 一番上 に記載 max 𝒘𝒘 𝒘𝒘Τ 𝑆𝑆𝐵𝐵 𝒘𝒘 s.t. 𝒘𝒘Τ 𝑆𝑆𝑊𝑊 𝒘𝒘 = 1
- 16. 内容： 24 判別分析とは 線形判別分析の基礎 直線を用いたカテゴリ判別 カテゴリ間分散・カテゴリ内分散による定式化 直線の最適化 線形判別分析の応用 手順 Pythonによる実装例
- 17. 線形判別分析の手順 25 以下の学習データに対して、線形判別分析を行う ステップ１：各カテゴリの平均を求める 𝑥𝑥1 𝑥𝑥2 カテゴリ 3 4 P 4 5 P 5 9 P 9 5 Q 8 4 Q 7 3 Q 6𝑜𝑜 𝑥𝑥1 𝑥𝑥2 5 平均値𝐦𝐦 = 6,5 カテゴリPの平均𝒎𝒎𝑃𝑃 = 1 3 3 4 + 4 5 + 5 9 = 1 3 12 18 = 4 6 カテゴリQの平均𝒎𝒎𝑄𝑄 = 1 3 9 5 + 8 4 + 7 3 = 1 3 24 12 = 8 4
- 18. 線形判別分析手順2 26 ステップ2： 行列𝑆𝑆𝐵𝐵、𝑆𝑆𝑊𝑊および𝑆𝑆𝑊𝑊 −1 を求める 𝑆𝑆𝐵𝐵 = 𝒎𝒎𝑃𝑃 − 𝒎𝒎𝑄𝑄 𝒎𝒎𝑃𝑃 − 𝒎𝒎𝑄𝑄 Τ = 4 6 − 8 4 4 6 − 8 4 Τ = −4 2 −4 2 Τ = 16 −8 −8 4 𝒎𝒎𝑃𝑃 = 4 6 𝒎𝒎𝑄𝑄 = 8 4 𝑆𝑆𝑊𝑊 = � 𝑖𝑖∈𝑃𝑃 𝒙𝒙𝑖𝑖 − 𝒎𝒎𝑃𝑃 𝒙𝒙𝑖𝑖 − 𝒎𝒎𝑃𝑃 Τ + � 𝑖𝑖∈𝑄𝑄 𝒙𝒙𝑖𝑖 − 𝒎𝒎𝑄𝑄 𝒙𝒙𝑖𝑖 − 𝒎𝒎𝑄𝑄 Τ 𝑥𝑥1 𝑥𝑥2 カテ ゴリ 3 4 P 4 5 P 5 9 P 9 5 Q 8 4 Q 7 3 Q = 3 4 − 4 6 3 4 − 4 6 Τ + 4 5 − 4 6 4 5 − 4 6 Τ + 5 9 − 4 6 5 9 − 4 6 Τ + 9 5 − 8 4 9 5 − 8 4 Τ + 8 4 − 8 4 8 4 − 8 4 Τ + 7 3 − 7 3 8 4 − 8 4 Τ = 1 2 2 4 + 0 0 0 1 + 1 3 3 9 + 1 1 1 1 + 0 0 0 0 + 1 1 1 1 = 4 7 7 16 𝑆𝑆𝑊𝑊 −1 = 1 15 16 −7 −7 4
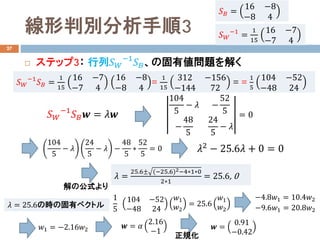
- 19. 線形判別分析手順3 27 ステップ3： 行列𝑆𝑆𝑊𝑊 −1 𝑆𝑆𝐵𝐵、の固有値問題を解く 𝑆𝑆𝐵𝐵 = 16 −8 −8 4 𝑆𝑆𝑊𝑊 −1 = 1 15 16 −7 −7 4 𝑆𝑆𝑊𝑊 −1 𝑆𝑆𝐵𝐵 = 1 15 16 −7 −7 4 16 −8 −8 4 = 1 15 312 −156 −144 72 = = 1 5 104 −52 −48 24 𝑆𝑆𝑊𝑊 −1 𝑆𝑆𝐵𝐵 𝒘𝒘 = 𝜆𝜆𝒘𝒘 104 5 − 𝜆𝜆 − 52 5 − 48 5 24 5 − 𝜆𝜆 = 0 104 5 − 𝜆𝜆 24 5 − 𝜆𝜆 − 48 5 ∗ 52 5 = 0 𝜆𝜆 = 25.6± (−25.6)2−4∗1∗0 2∗1 = 25.6, 0 解の公式より 𝜆𝜆2 − 25.6𝜆𝜆 + 0 = 0 𝜆𝜆 = 25.6の時の固有ベクトル 1 5 104 −52 −48 24 𝑤𝑤1 𝑤𝑤2 = 25.6 𝑤𝑤1 𝑤𝑤2 −4.8𝑤𝑤1 = 10.4𝑤𝑤2 −9.6𝑤𝑤1 = 20.8𝑤𝑤2 𝑤𝑤1 = −2.16𝑤𝑤2 𝒘𝒘 = 𝛼𝛼 2.16 −1 𝒘𝒘 = 0.91 −0.42正規化
- 20. 線形判別分析手順4 28 ステップ4：求めた𝒘𝒘を用いて、直線𝑧𝑧のモデル式を作成 ステップ5：直線𝑧𝑧をグラフに描き、学習データのカテゴリが 分離（判別）できることを確認 ステップ6:未知のデータのカテゴリを予測 直線𝑧𝑧のモデル式： �𝑦𝑦 = 𝑤𝑤1 𝑥𝑥1 − 𝑥𝑥1 + 𝑤𝑤2 𝑥𝑥2 − 𝑥𝑥2 = 0.91 𝑥𝑥1 − 6 − 0.42 𝑥𝑥2 − 5 平均𝐦𝐦 = 6,5 Τ 𝒘𝒘 = 0.91 −0.42
- 21. 演習4 29 1. 線形判別分析により求めた直線をグラフに描き、 学習データのカテゴリが分離できていることを確認しなさい。 2. 新しいデータ 1,5 Τと 7,2 Τのカテゴリを予測しなさい。 タイトル「演習レポート」、日付、学生番号、氏名を用紙の 一番上に記載 6𝑜𝑜 𝑥𝑥1 𝑥𝑥2 5 平均値𝐦𝐦 = 6,5 �𝑦𝑦 = 0.91 𝑥𝑥1 − 6 − 0.42 𝑥𝑥2 − 5 𝑥𝑥1 𝑥𝑥2 カテ ゴリ 3 4 P 4 5 P 5 9 P 9 5 Q 8 4 Q 7 3 Q 1 5 ？ 7 2 ？
- 22. 内容： 31 判別分析とは 線形判別分析の基礎 直線を用いたカテゴリ判別 カテゴリ間分散・カテゴリ内分散による定式化 直線の最適化 線形判別分析の応用 手順 Pythonによる実装例
- 24. 課題 33 数学と英語の点数データに関する行列𝑆𝑆𝑊𝑊 −1 𝑆𝑆𝐵𝐵 = 0.83 0.4 0.68 0.32 、 平均𝐦𝐦 = 4.2,3.8 Τのとき、線形判別分析を行いなさい。 1. 固有値問題を解き、直線𝑧𝑧の正規基底ベクトル𝒘𝒘を求めなさい。 2. 直線𝑧𝑧のモデル式を書きなさい。 3. グラフに点数データと、求めた直線𝑧𝑧および分類境界を描きなさい。 4. 直線𝑧𝑧により、点数データのカテゴリが判別できるか否か考察しなさい。 5. 新しい学生の点数 0,8 Τ と 1,8 Τ を判別しなさい。 A B C D E F G H I J 数学𝑥𝑥1 2 1 2 3 5 4 8 6 7 4 英語𝑥𝑥2 3 4 2 2 4 4 5 3 6 5 カテゴリ P P P P Q Q Q Q Q Q 数学と英語の点数データ
- 25. レポートの提出方法 34 演習レポート： タイトル「演習レポート」、日付・学生番号・氏名を用紙の一番上に記載 課題レポート ： タイトル「課題レポート」、出題日・学生番号・氏名を用紙の一番上に記載 2ページ以上になる場合は、ホッチキス留め A4サイズの用紙を使用 一度に複数の課題レポートを提出する場合出題日ごとに別々に綴じる