Download as PDF, PPTX
![[第2回3D勉強会 研究紹介] Neural 3D Mesh Renderer (CVPR 2018)](https://cdn.slidesharecdn.com/ss_thumbnails/201807263dv-180728060959-thumbnail.jpg?width=640&height=640&fit=bounds)
わかりやすいパターン認識_3章
- 1.
- 2. 2 自己紹介 TwitterID : weda_654 所属: GoogleMapとAWSとデータ分析の会社 業務 : データ分析(実力はお察し) 使用言語 : R(メイン), Python(たまに) こんなアイコン
- 3.
- 4.
- 5.
- 6.
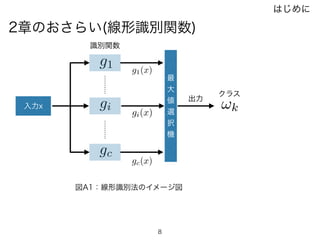
- 7. 7 2章のおさらい(線形識別関数) はじめに g(x) = w0+ dX j=1 wjxj g(x) = w0 + wt x g(x) = Wt X w0, w1, ..., wd重み係数 ベクトルで表現 d+1次元の拡張(特徴・重み)ベクトルを使用 w = (w1, ..., wd)t x = (x1, ..., xd)t W = (w0, w)t X = (x0, x)t (3a) (3b) (3c)
- 8.
- 9.
- 10. 10 2章のおさらい(パーセプトロンの学習規則) (1) 重みベクトルW の初期値を適当に選ぶ (2)の中から学習パターンを1つ選ぶ (3) 識別関数 g(x) = Wt X によって識別を行い 正しく識別できなかった場合のみ修正を行いW 0 を作る (4) (2),(3)を の全パターンで繰り返す (5) の全パターンを正しく認識すれば終了 誤りがあれば(2)へ戻る W 0 = W ± ⇢X (⇢ > 0) (7) はじめに
- 11. 11 2章のおさらい(パーセプトロンの収束定理) が線形分離可能ならば,パーセプトロンの学習規則を 有限回繰り返すことで解領域の重みベクトルに達する パーセプトロンの収束定理による学習はΦ関数の重みに 対して適用できる Φ関数 x 1(x),2(x), ..., d(x)の任意の関数 の 線形結合で表される関数 はじめに
- 12. 12 記号について w = (w1,w2, ..., wd)t x = (x1, x2, ..., xd)t X = (x0, x)t W = (w0, W)t Xpatt = (X1, ..., Xp, ..., Xn)t : 特徴ベクトル : 拡張特徴ベクトル : 重みベクトル : 拡張重みベクトル : パターン行列 はじめに
- 13.
- 14.
- 15.
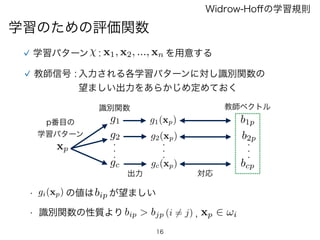
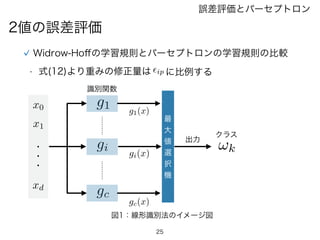
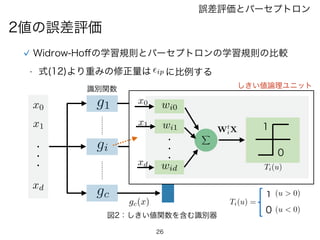
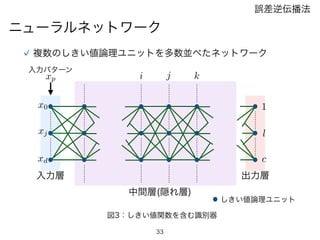
- 16. 16 学習のための評価関数 Widrow-Hoffの学習規則 学習パターン : x1,x2, ..., xn を用意する 教師信号 : 入力される各学習パターンに対し識別関数の 望ましい出力をあらかじめ定めておく xp g1 g2 gc gc(xp) g2(xp) g1(xp) b1p b2p bcp p番目の 学習パターン 識別関数 ・・・ ・・・ ・・・ 教師ベクトル 対応 gi(xp) の値はbip が望ましい• • 識別関数の性質より bip > bjp (i 6= j) xp 2 !i, 出力
- 17. 17 学習のための評価関数 Widrow-Hoffの学習規則 入力パターンxp に対する出力と教師信号の誤差を とおく✏ip ✏ip= gi(xp) bip 式(1)の2乗和を評価関数 Jp とすると Jp(W1, W2, ..., Wc) = 1 2 cX i=1 ✏2 ip = 1 2 cX i=1 (gi(xp) bip)2 = 1 2 cX i=1 (Wt iXp bip)2 (2) (1)
- 18. 18 学習のための評価関数 Widrow-Hoffの学習規則 全ての入力パターンに対する評価関数は J(W1, W2, ...,Wc) = Jp nX p=1 (W1, W2, ..., Wc) Jp(W) = 1 2 (g(xp) bp)2 = 1 2 (Wt Xp bp)2 (3) bp = (xp 2 !1) (xp 2 !2) 1 -1 2クラスにおける式(2)は式(4)のように表せる (4) • 教師信号は下記のような設定が考えられる
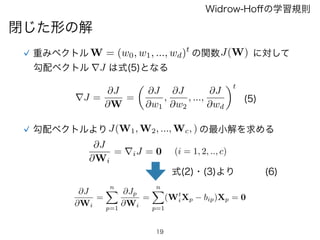
- 19. 19 閉じた形の解 Widrow-Hoffの学習規則 重みベクトル W =(w0, w1, ..., wd)t の関数J(W) に対して 勾配ベクトル rJ は式(5)となる (5)rJ = @J @W = ✓ @J @w1 , @J @w2 , ..., @J @wd ◆t 勾配ベクトルよりJ(W1, W2, ..., Wc, ) の最小解を求める @J @Wi = riJ = 0 (i = 1, 2, .., c) (6) @J @Wi = nX p=1 @Jp @Wi = nX p=1 (Wt iXp bip)Xp = 0 式(2)・(3)より
- 20. 20 閉じた形の解 Widrow-Hoffの学習規則 ベクトルの定義 Xpatt = (X1,X2, ..., Xn)t (i = 1, 2, .., c)bi = (bi1, bi2, ..., bin)t (7) ベクトルの定義により式(2)・(3)を書き換えると J(W1, W2, ..., Wc) = 1 2 cX i=1 kXpattWi bik2 勾配ベクトルは… @J @Wi = Xt patt(XpattWi bi) = 0 (i = 1, 2, .., c) (8) (9) パターン行列
- 21. 21 閉じた形の解 Widrow-Hoffの学習規則 式(9)より Wi = (Xt pattXpatt)1 Xpattbi (10) 評価関数Jが最小となるWiは(Xt pattXpatt) 1 Xpattbi である
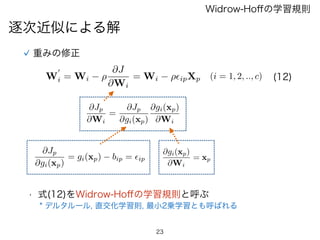
- 22. 22 逐次近似による解 Widrow-Hoffの学習規則 閉じた形の解における問題点 • Wi はXt pattXpatt が正則でなくては用いることができない • 次元が大きくなると逆行列の計算が大変 代替案 • 逐次近似により重みを決定すれば良い * 最もよく使われるのは最急降下法 W 0 i = Wi ⇢ @J @Wi = Wi ⇢riJ (i = 1, 2, .., c) (11) • 式(11)より学習パターンを逐次更新していき最終的に Jの最小解にたどり着く ⇢は刻み幅
- 23. 23 逐次近似による解 Widrow-Hoffの学習規則 重みの修正 @Jp @Wi = @Jp @gi(xp) @gi(xp) @Wi @Jp @gi(xp) = gi(xp) bip= ✏ip @gi(xp) @Wi = xp W 0 i = Wi ⇢ @J @Wi = Wi ⇢✏ipXp (i = 1, 2, .., c) (12) • 式(12)をWidrow-Hoffの学習規則と呼ぶ * デルタルール, 直交化学習則, 最小2乗学習とも呼ばれる
- 24.
- 25. 25 2値の誤差評価 誤差評価とパーセプトロン Widrow-Hoffの学習規則とパーセプトロンの学習規則の比較 • 式(12)より重みの修正量は ✏ipに比例する gc(x) gi(x) g1(x) 識別関数 g1 gi gc 最 大 値 選 択 機 出力 !k クラス x0 x1 xd ・・・ 図1：線形識別法のイメージ図
- 26. 26 2値の誤差評価 誤差評価とパーセプトロン Widrow-Hoffの学習規則とパーセプトロンの学習規則の比較 • 式(12)より重みの修正量は ✏ipに比例する gc(x) gi(x) g1(x) 識別関数 g1 gi gc 最 大 値 選 択 機 出力 !k クラス x0 x1 xd ・・・ wi0 wid X ・・・ Wt iX 1 0 Ti(u) xd x0 x1 wi1 図2：しきい値関数を含む識別器 1 0 (u > 0) (u < 0) Ti(u) = しきい値論理ユニット
- 27.
- 28. 28 2値の誤差評価 誤差評価とパーセプトロン Widrow-Hoffの学習規則とパーセプトロンの学習規則の比較 Wt iX > 0 Wt iX< 0 • 式(13)が成り立つように重みベクトルを調整すると… (13) 式(13)としきい値関数より (14) x 2 !i x 62 !i (j 6= i) (j = 1, 2, ..., c) gi(x) = 1 gj(x) = 0
- 29. 29 2値の誤差評価 誤差評価とパーセプトロン Widrow-Hoffの学習規則とパーセプトロンの学習規則の比較 • 教師信号 bip = 1 0(xp 62 !i) (xp 2 !i) bip = 1 bjp = 0 gi(xp) = 0 gj(xp) = 1 , , (j 6= i) • 教師信号を設定することで誤認識の確認ができる (15) (16)
- 30. 30 2値の誤差評価 誤差評価とパーセプトロン 式(12)と(16)より重みベクトルの修正法は… W 0 i = Wi⇢Xp W 0 j = Wj + ⇢Xp (17) • 式(17)はパーセプトロンの学習規則の修正法と同じになる Widrow-Hoffの学習規則はパーセプトロンの学習規則を 特別な場合として含んでいる
- 31.
- 32.
- 33.
- 34.
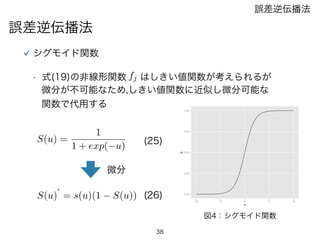
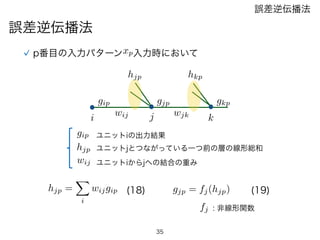
- 35. 35 ji k xp gip hjp hkp gjpgkp wij 誤差逆伝播法 誤差逆伝播法 wjk p番目の入力パターン 入力時において ユニットiの出力結果gip ユニットjとつながっている一つ前の層の線形総和 ユニットiからjへの結合の重み hjp wij hjp = X i wijgip gjp = fj(hjp)(18) (19) fj : 非線形関数
- 36. 36 誤差逆伝播法 誤差逆伝播法 評価関数はこれまでと同様に… J = X p Jp Jの最小解はWidrow-Hoffと同じく最急降下法で求まる * 出力層のl番目のユニットの評価関数 Jp= X l (glp blp)2 (21)(20) * 出力層のj番目のユニットの評価関数を微分 @Jp @wij = @Jp @hjp @hjp @wjp @Jp @hjp = ✏jp @hjp @wjp = gip , = ✏jpgip (22)
- 37. 37 誤差逆伝播法 誤差逆伝播法 ✏jp の決定 ✏jp = @Jp @hjp = @Jp @gjp @gjp @hjp = @Jp @gjp f 0 j(hjp) *式(19)・(22)より 出力層・中間層で場合分けを行う 出力層 @Jp @gjp = gjp bjp @Jp @gjp = X k @Jp @hkp @hkp @gjp 中間層 @Jp @hkp = ✏kp @hkp @gjp = wjk = X k ✏kpwjk (23) (24)
- 38. 38 誤差逆伝播法 誤差逆伝播法 シグモイド関数 • 式(19)の非線形関数 fjはしきい値関数が考えられるが 微分が不可能なため,しきい値関数に近似し微分可能な 関数で代用する S(u) = 1 1 + exp( u) 図4：シグモイド関数 (25) 微分 S(u) 0 = s(u)(1 S(u)) (26)
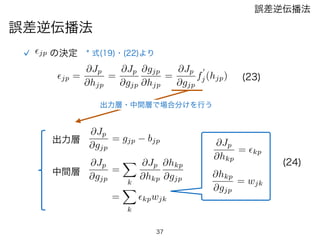
- 39. 39 誤差逆伝播法 誤差逆伝播法 非線形関数fj の変形 *式(19)・(26)より fj(hjp) 0 = gjp(1 gjp) (27) ✏jp は次のように求まる X k ✏kpwjk ! gjp(1 gjp) (gjp bjp)gjp(1 gjp) ✏jp = (ユニットjが出力層にあるとき) (ユニットjが中間層にあるとき) (28a) (28b)
- 40.