Download as PDF, PPTX
![[DL輪読会]Temporal Abstraction in NeurIPS2019](https://cdn.slidesharecdn.com/ss_thumbnails/20191115-191112082849-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]Control as Inferenceと発展](https://cdn.slidesharecdn.com/ss_thumbnails/20191004-191204055019-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]Recent Advances in Autoencoder-Based Representation Learning](https://cdn.slidesharecdn.com/ss_thumbnails/20190119dljournalclubweb-190401063633-thumbnail.jpg?width=640&height=640&fit=bounds)
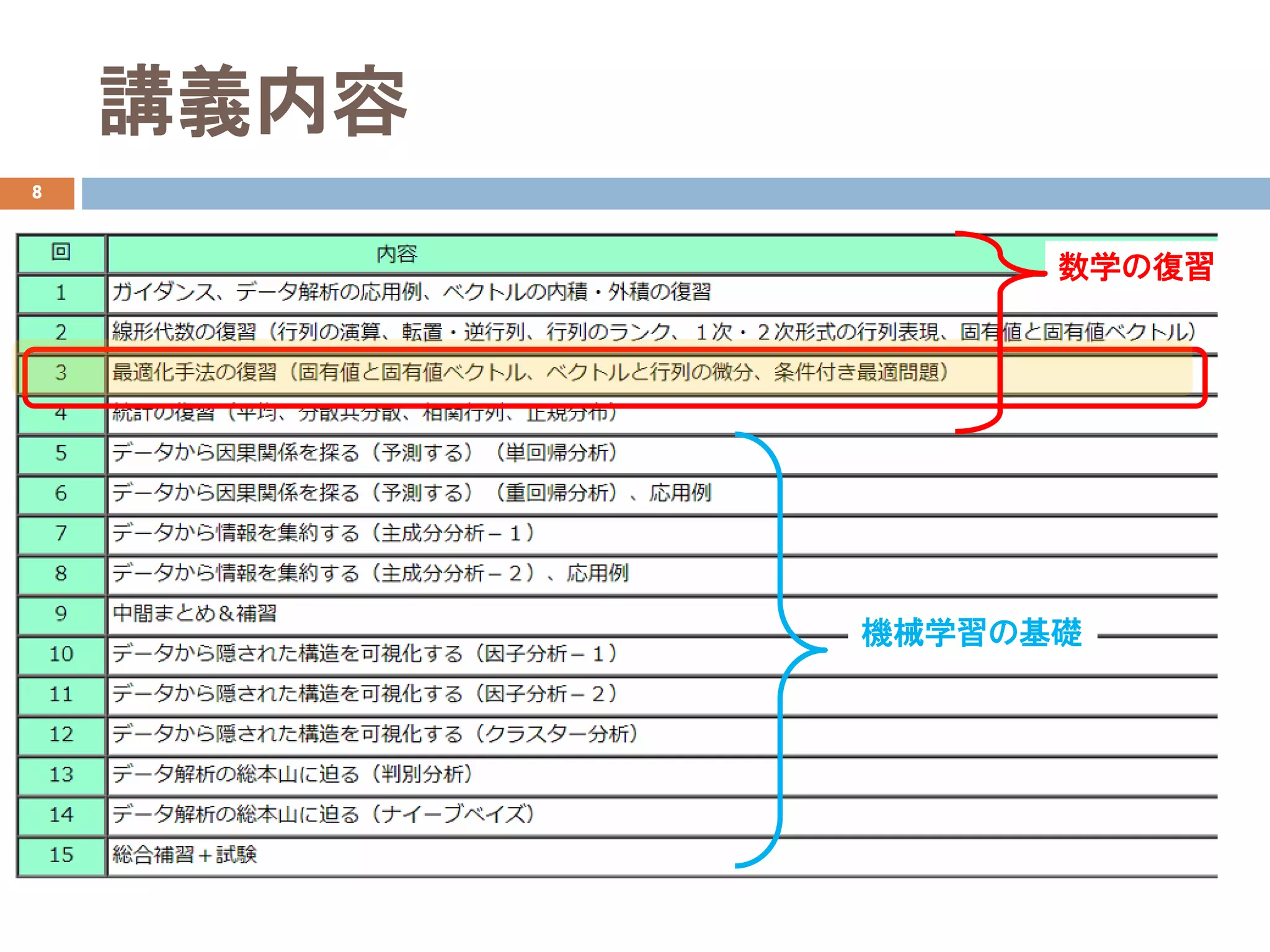
データ解析3 最適化の復習
- 1.
- 2.
- 3. 内容：最適化手法の復習 9 連立方程式の解法 行列演算を用いた方法 制約なしの最適化問題の解法 微分を用いた方法 偏微分を用いた方法 行列、ベクトルの微分 制約ありの最適化問題の解法 ラグランジュ未定乗数法
- 4. 行列演算による連立方程式の解法 10 2元1次連立方程式の行列表現 行列式|𝑨𝑨|≠ 0なら、逆行列𝑨𝑨−𝟏𝟏 が存在 連立方程式の解を解析的に一意（確定的）に求められる � 𝑎𝑎𝑎𝑎 + 𝑏𝑏𝑏𝑏 = 𝑘𝑘 𝑐𝑐𝑥𝑥 + 𝑏𝑏𝑏𝑏 = 𝑙𝑙 𝑎𝑎 𝑏𝑏 𝑐𝑐 𝑑𝑑 𝑥𝑥 𝑦𝑦 = 𝑘𝑘 𝑙𝑙 𝑨𝑨𝑨𝑨 = 𝒃𝒃 𝑨𝑨−𝟏𝟏 𝑨𝑨𝑨𝑨 = 𝑨𝑨−𝟏𝟏 𝒃𝒃 𝒙𝒙 = 𝑨𝑨−𝟏𝟏 𝒃𝒃 正則行列𝑨𝑨 |𝑨𝑨| ≠ 0
- 5. 2次正方行列の逆行列 11 行列式が0の場合：逆行列は無限に発散するため存在しない 逆行列の計算例： 逆行列が正しいか否かの確認 𝑎𝑎 𝑏𝑏 𝑐𝑐 𝑑𝑑 −1 = 1 𝑎𝑎𝑎𝑎−𝑏𝑏𝑏𝑏 𝑑𝑑 −𝑏𝑏 −𝑐𝑐 𝑎𝑎 行列式と等しい 3 2 5 1 −1 = − 1 7 1 −2 −5 3 − 1 7 1 −2 −5 3 3 2 5 1 = − 1 7 −7 0 0 −7 = 1 0 0 1 𝐴𝐴𝐴𝐴−1 = 𝐼𝐼
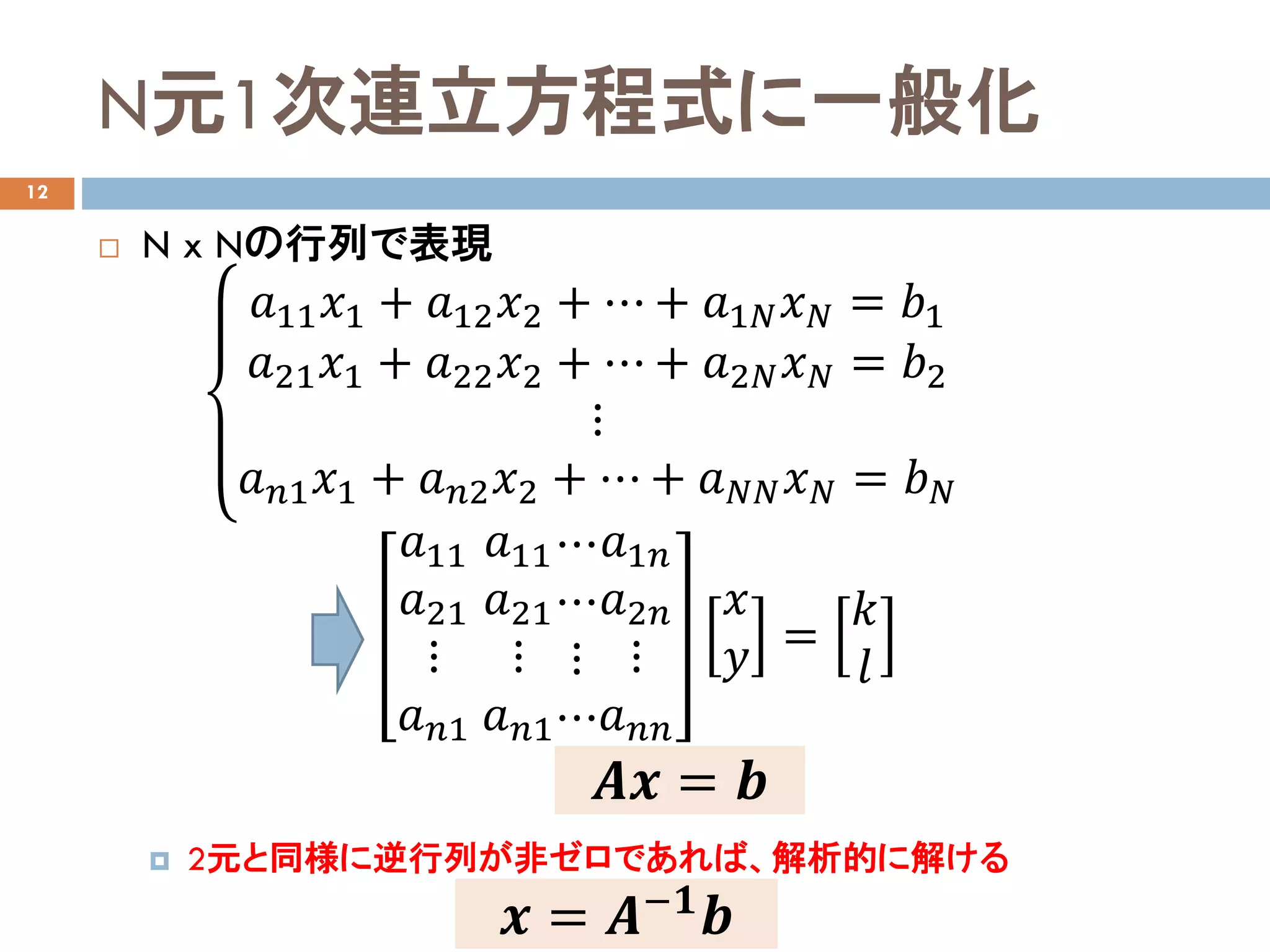
- 6. N元1次連立方程式に一般化 12 N xNの行列で表現 2元と同様に逆行列が非ゼロであれば、解析的に解ける 𝑎𝑎11 𝑥𝑥1 + 𝑎𝑎12 𝑥𝑥2 + ⋯ + 𝑎𝑎1𝑁𝑁 𝑥𝑥𝑁𝑁 = 𝑏𝑏1 𝑎𝑎21 𝑥𝑥1 + 𝑎𝑎22 𝑥𝑥2 + ⋯ + 𝑎𝑎2𝑁𝑁 𝑥𝑥𝑁𝑁 = 𝑏𝑏2 ⋮ 𝑎𝑎𝑛𝑛1 𝑥𝑥1 + 𝑎𝑎𝑛𝑛2 𝑥𝑥2 + ⋯ + 𝑎𝑎𝑁𝑁𝑁𝑁 𝑥𝑥𝑁𝑁 = 𝑏𝑏𝑁𝑁 𝑎𝑎11 𝑎𝑎21 ⋮ 𝑎𝑎𝑛𝑛𝑛 𝑎𝑎11 𝑎𝑎21 ⋮ 𝑎𝑎𝑛𝑛𝑛 ⋯ ⋯ ⋮ ⋯ 𝑎𝑎1𝑛𝑛 𝑎𝑎2𝑛𝑛 ⋮ 𝑎𝑎𝑛𝑛𝑛𝑛 𝑥𝑥 𝑦𝑦 = 𝑘𝑘 𝑙𝑙 𝑨𝑨𝑨𝑨 = 𝒃𝒃 𝒙𝒙 = 𝑨𝑨−𝟏𝟏 𝒃𝒃
- 7. 演習1 13 以下の2元1次連立方程式の解が一意に求められるか確認 し、解を求めなさい。 タイトル「演習レポート」、日付、学生番号、氏名を用紙の 一番上に記載 � 2𝑥𝑥− 3𝑦𝑦 = 5 4𝑥𝑥 + 𝑦𝑦 = −2
- 8. 様々な連立方程式の行列表現 15 1次形式（linear form）の行列表現 双1次形式（bilinear form）の行列表現 2次形式（quadratic form）の行列表現 𝑎𝑎11 𝑎𝑎12 𝑎𝑎21 𝑎𝑎22 𝑥𝑥1 𝑥𝑥2 = 𝑏𝑏1 𝑏𝑏2 𝑨𝑨𝑨𝑨 = 𝒃𝒃 𝒚𝒚𝚻𝚻 𝑨𝑨𝑨𝑨 = 𝒃𝒃 𝒙𝒙𝚻𝚻 𝑨𝑨𝑨𝑨 = 𝒃𝒃𝑥𝑥1 𝑥𝑥2 𝑎𝑎11 𝑎𝑎12 𝑎𝑎21 𝑎𝑎22 𝑥𝑥1 𝑥𝑥2 = 𝑏𝑏1 𝑏𝑏2 𝑦𝑦1 𝑦𝑦2 𝑎𝑎11 𝑎𝑎12 𝑎𝑎21 𝑎𝑎22 𝑥𝑥1 𝑥𝑥2 = 𝑏𝑏1 𝑏𝑏2
- 9. 内容：最適化手法の復習 16 連立方程式の解法 行列演算を用いた方法 制約なしの最適化問題の解法 微分を用いた方法 偏微分を用いた方法 行列、ベクトルの微分 制約ありの最適化問題の解法 ラグランジュ未定乗数法
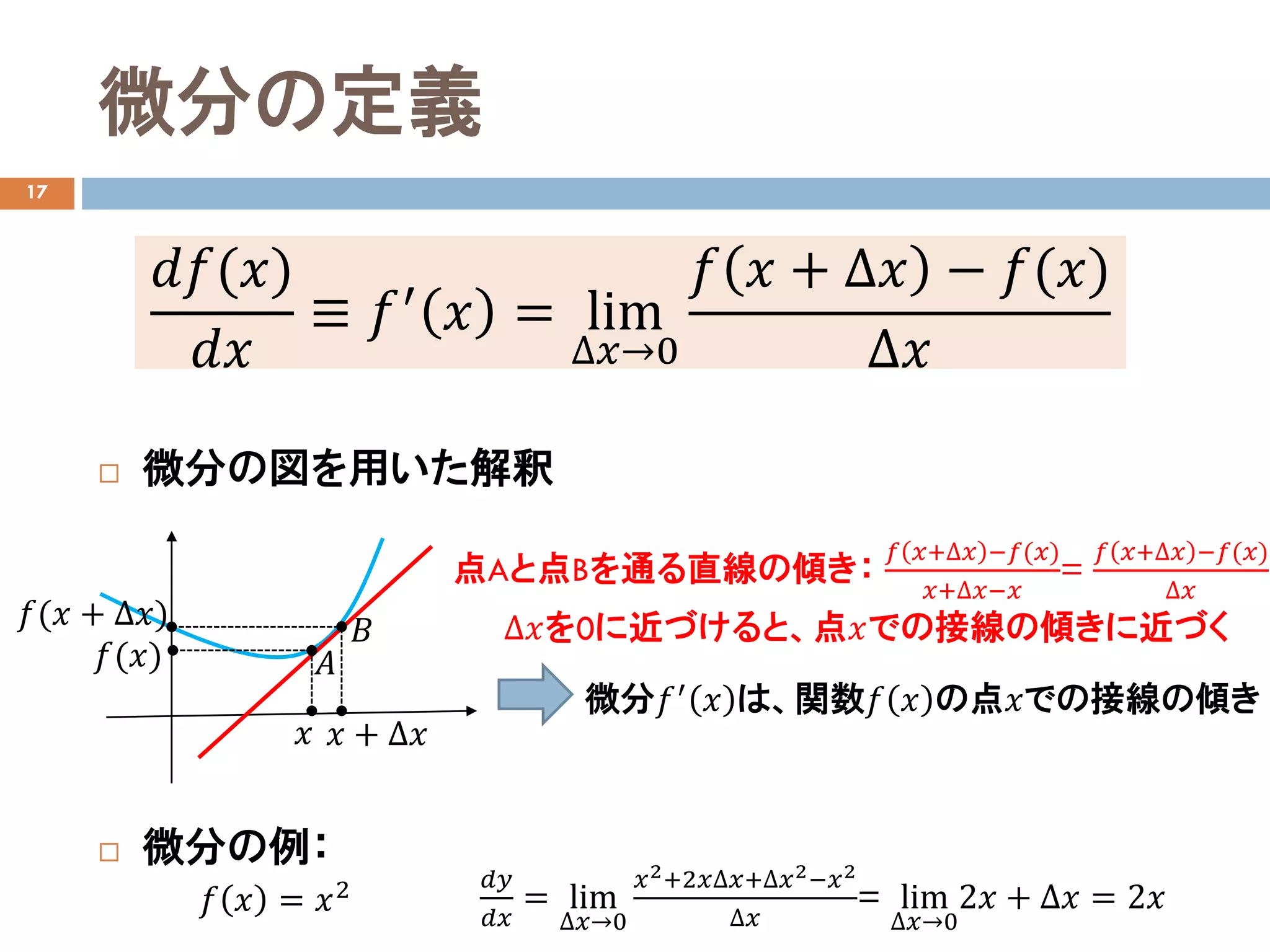
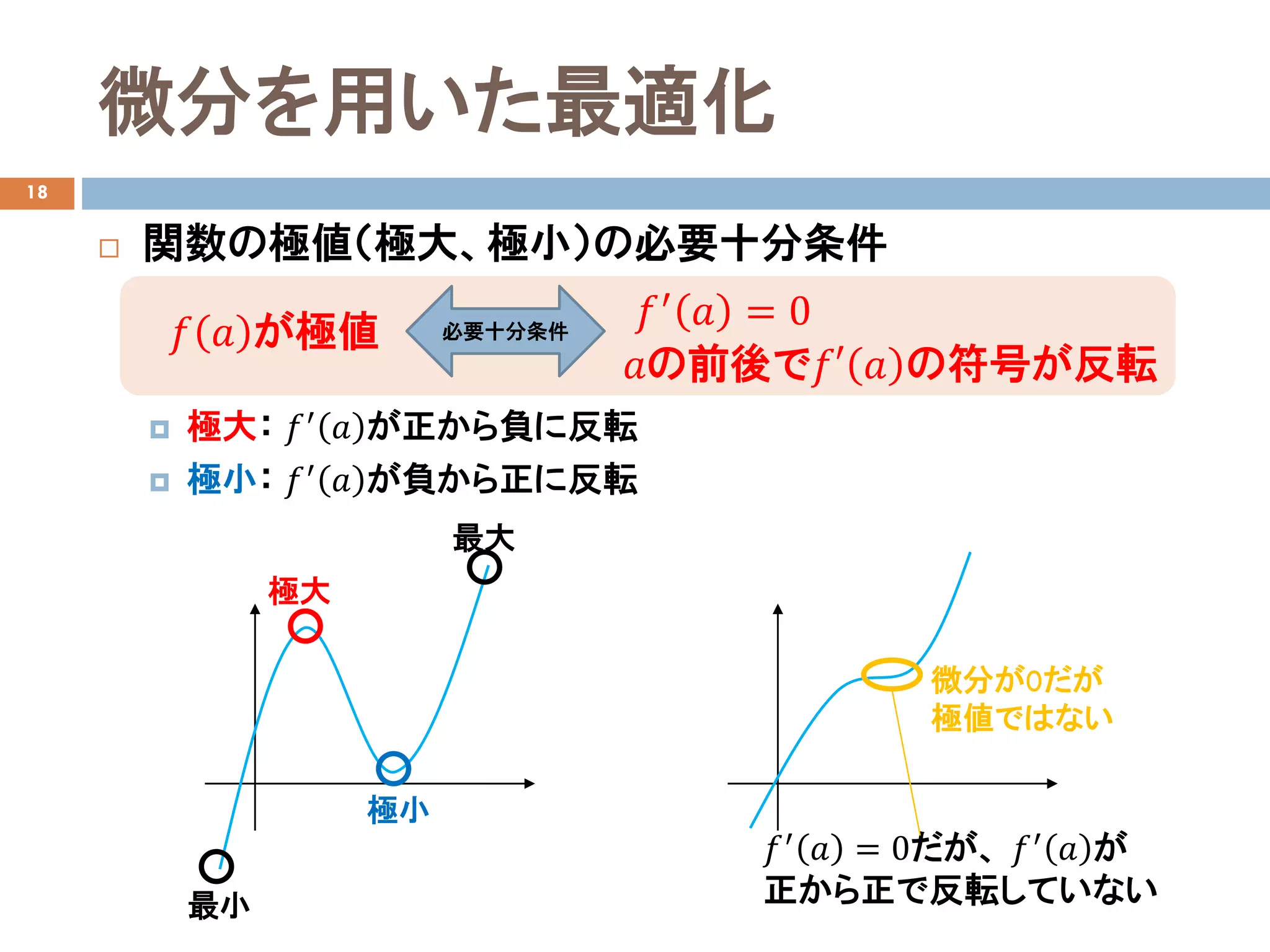
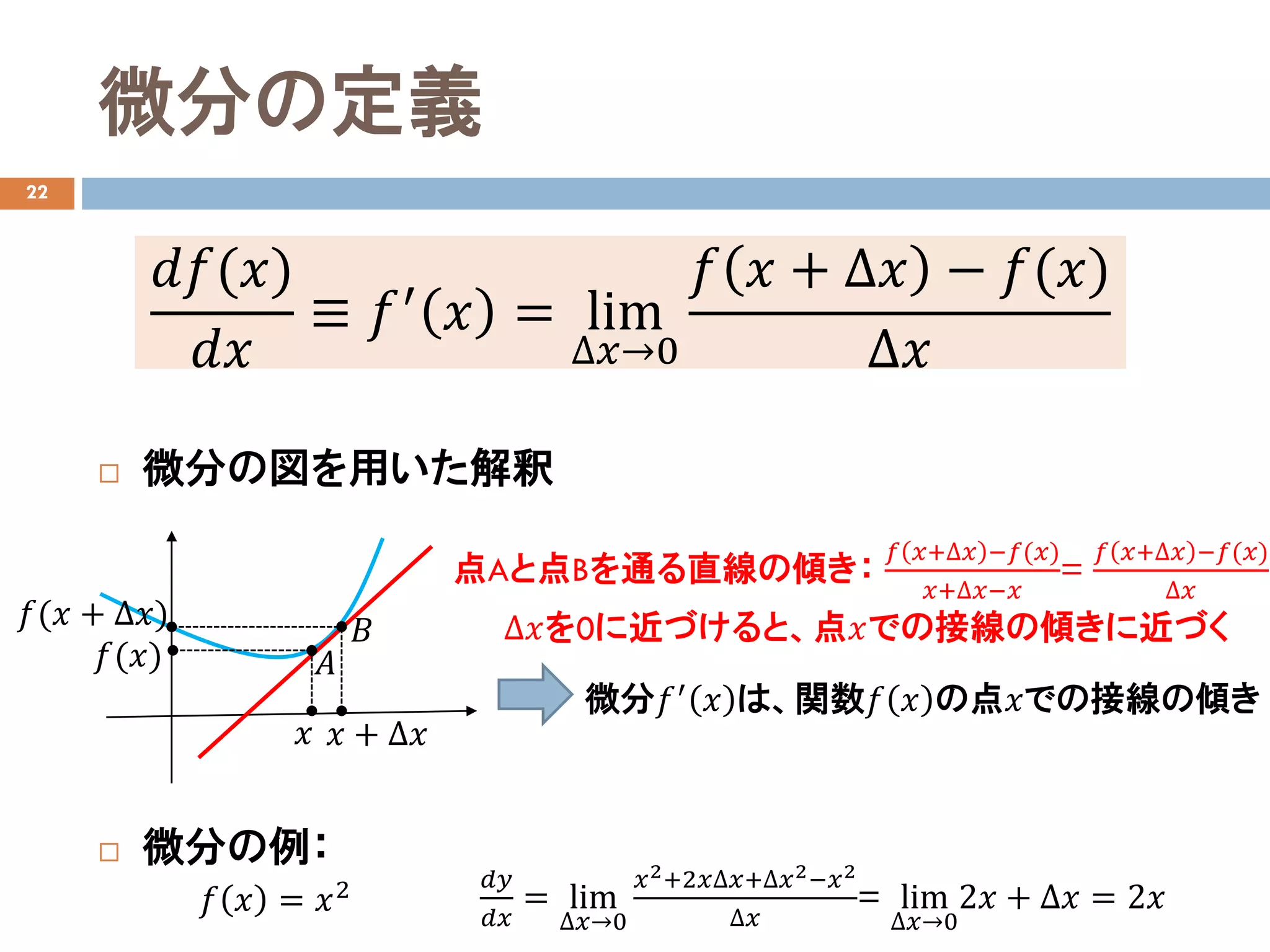
- 10. 微分の定義 17 微分の図を用いた解釈 微分の例： 𝑑𝑑𝑓𝑓(𝑥𝑥) 𝑑𝑑𝑑𝑑 ≡𝑓𝑓′ 𝑥𝑥 = lim ∆𝑥𝑥→0 𝑓𝑓 𝑥𝑥 + ∆𝑥𝑥 − 𝑓𝑓(𝑥𝑥) ∆𝑥𝑥 𝑓𝑓(𝑥𝑥) 𝑥𝑥 𝑥𝑥 + ∆𝑥𝑥 𝑓𝑓(𝑥𝑥 + ∆𝑥𝑥) 点Aと点Bを通る直線の傾き： 𝑓𝑓 𝑥𝑥+∆𝑥𝑥 −𝑓𝑓(𝑥𝑥) 𝑥𝑥+∆𝑥𝑥−𝑥𝑥 = 𝑓𝑓 𝑥𝑥+∆𝑥𝑥 −𝑓𝑓(𝑥𝑥) ∆𝑥𝑥 ∆𝑥𝑥を0に近づけると、点𝑥𝑥での接線の傾きに近づく 𝐴𝐴 𝐵𝐵 微分𝑓𝑓′ 𝑥𝑥 は、関数𝑓𝑓 𝑥𝑥 の点𝑥𝑥での接線の傾き 𝑓𝑓 𝑥𝑥 = 𝑥𝑥2 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 = lim ∆𝑥𝑥→0 𝑥𝑥2+2𝑥𝑥∆𝑥𝑥+∆𝑥𝑥2−𝑥𝑥2 ∆𝑥𝑥 = lim ∆𝑥𝑥→0 2𝑥𝑥 + ∆𝑥𝑥 = 2𝑥𝑥
- 11. 微分を用いた最適化 18 関数の極値（極大、極小）の必要十分条件 極大：𝑓𝑓′ 𝑎𝑎 が正から負に反転 極小： 𝑓𝑓′ 𝑎𝑎 が負から正に反転 𝑓𝑓′ 𝑎𝑎 = 0 𝑓𝑓 𝑎𝑎 が極値 必要十分条件 𝑎𝑎の前後で𝑓𝑓𝑓 𝑎𝑎 の符号が反転 極大 極小 最大 最小 𝑓𝑓′ 𝑎𝑎 = 0だが、 𝑓𝑓′ 𝑎𝑎 が 正から正で反転していない 微分が0だが 極値ではない
- 12. 演習2 19 極大値と極小値を求めなさい。 タイトル「演習レポート」、日付、学生番号、氏名を用紙の 一番上に記載 𝑓𝑓𝑥𝑥 = 𝑥𝑥3 − 12𝑥𝑥2 + 36𝑥𝑥 + 8
- 13. 内容：最適化手法の復習 21 連立方程式の解法 行列演算を用いた方法 制約なしの最適化問題の解法 微分を用いた方法 偏微分を用いた方法 行列、ベクトルの微分 制約ありの最適化問題の解法 ラグランジュ未定乗数法
- 14. 微分の定義 22 微分の図を用いた解釈 微分の例： 𝑑𝑑𝑓𝑓(𝑥𝑥) 𝑑𝑑𝑑𝑑 ≡𝑓𝑓′ 𝑥𝑥 = lim ∆𝑥𝑥→0 𝑓𝑓 𝑥𝑥 + ∆𝑥𝑥 − 𝑓𝑓(𝑥𝑥) ∆𝑥𝑥 𝑓𝑓(𝑥𝑥) 𝑥𝑥 𝑥𝑥 + ∆𝑥𝑥 𝑓𝑓(𝑥𝑥 + ∆𝑥𝑥) 点Aと点Bを通る直線の傾き： 𝑓𝑓 𝑥𝑥+∆𝑥𝑥 −𝑓𝑓(𝑥𝑥) 𝑥𝑥+∆𝑥𝑥−𝑥𝑥 = 𝑓𝑓 𝑥𝑥+∆𝑥𝑥 −𝑓𝑓(𝑥𝑥) ∆𝑥𝑥 ∆𝑥𝑥を0に近づけると、点𝑥𝑥での接線の傾きに近づく 𝐴𝐴 𝐵𝐵 微分𝑓𝑓′ 𝑥𝑥 は、関数𝑓𝑓 𝑥𝑥 の点𝑥𝑥での接線の傾き 𝑓𝑓 𝑥𝑥 = 𝑥𝑥2 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 = lim ∆𝑥𝑥→0 𝑥𝑥2+2𝑥𝑥∆𝑥𝑥+∆𝑥𝑥2−𝑥𝑥2 ∆𝑥𝑥 = lim ∆𝑥𝑥→0 2𝑥𝑥 + ∆𝑥𝑥 = 2𝑥𝑥
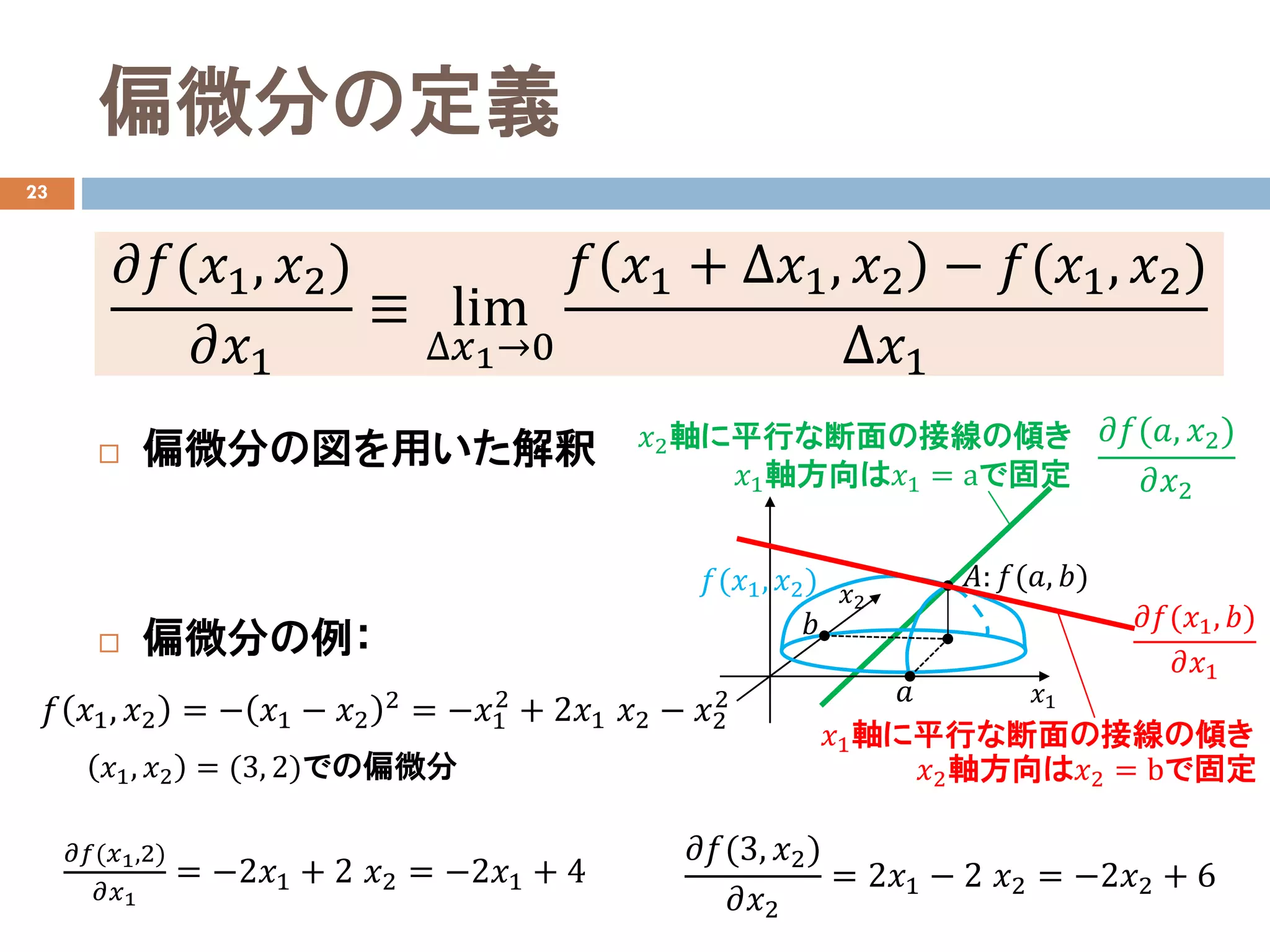
- 15. 偏微分の定義 23 偏微分の図を用いた解釈 偏微分の例： 𝜕𝜕𝑓𝑓(𝑥𝑥1,𝑥𝑥2) 𝜕𝜕𝑥𝑥1 ≡ lim ∆𝑥𝑥1→0 𝑓𝑓 𝑥𝑥1 + ∆𝑥𝑥1, 𝑥𝑥2 − 𝑓𝑓(𝑥𝑥1, 𝑥𝑥2) ∆𝑥𝑥1 𝑓𝑓 𝑥𝑥1, 𝑥𝑥2 = − 𝑥𝑥1 − 𝑥𝑥2 2 = −𝑥𝑥1 2 + 2𝑥𝑥1 𝑥𝑥2 − 𝑥𝑥2 2 𝑥𝑥1 𝑥𝑥2 𝐴𝐴: 𝑓𝑓(𝑎𝑎, 𝑏𝑏) 𝑎𝑎 𝑏𝑏 𝜕𝜕𝑓𝑓(𝑎𝑎, 𝑥𝑥2) 𝜕𝜕𝑥𝑥2 𝑥𝑥2軸に平行な断面の接線の傾き 𝑥𝑥1軸方向は𝑥𝑥1 = aで固定 𝜕𝜕𝑓𝑓(𝑥𝑥1, 𝑏𝑏) 𝜕𝜕𝑥𝑥1 𝑥𝑥1軸に平行な断面の接線の傾き 𝑥𝑥2軸方向は𝑥𝑥2 = bで固定 𝜕𝜕𝑓𝑓(𝑥𝑥1,2) 𝜕𝜕𝑥𝑥1 = −2𝑥𝑥1 + 2 𝑥𝑥2 = −2𝑥𝑥1 + 4 𝑥𝑥1, 𝑥𝑥2 = (3, 2)での偏微分 𝜕𝜕𝑓𝑓(3, 𝑥𝑥2) 𝜕𝜕𝑥𝑥2 = 2𝑥𝑥1 − 2 𝑥𝑥2 = −2𝑥𝑥2 + 6 𝑓𝑓(𝑥𝑥1, 𝑥𝑥2)
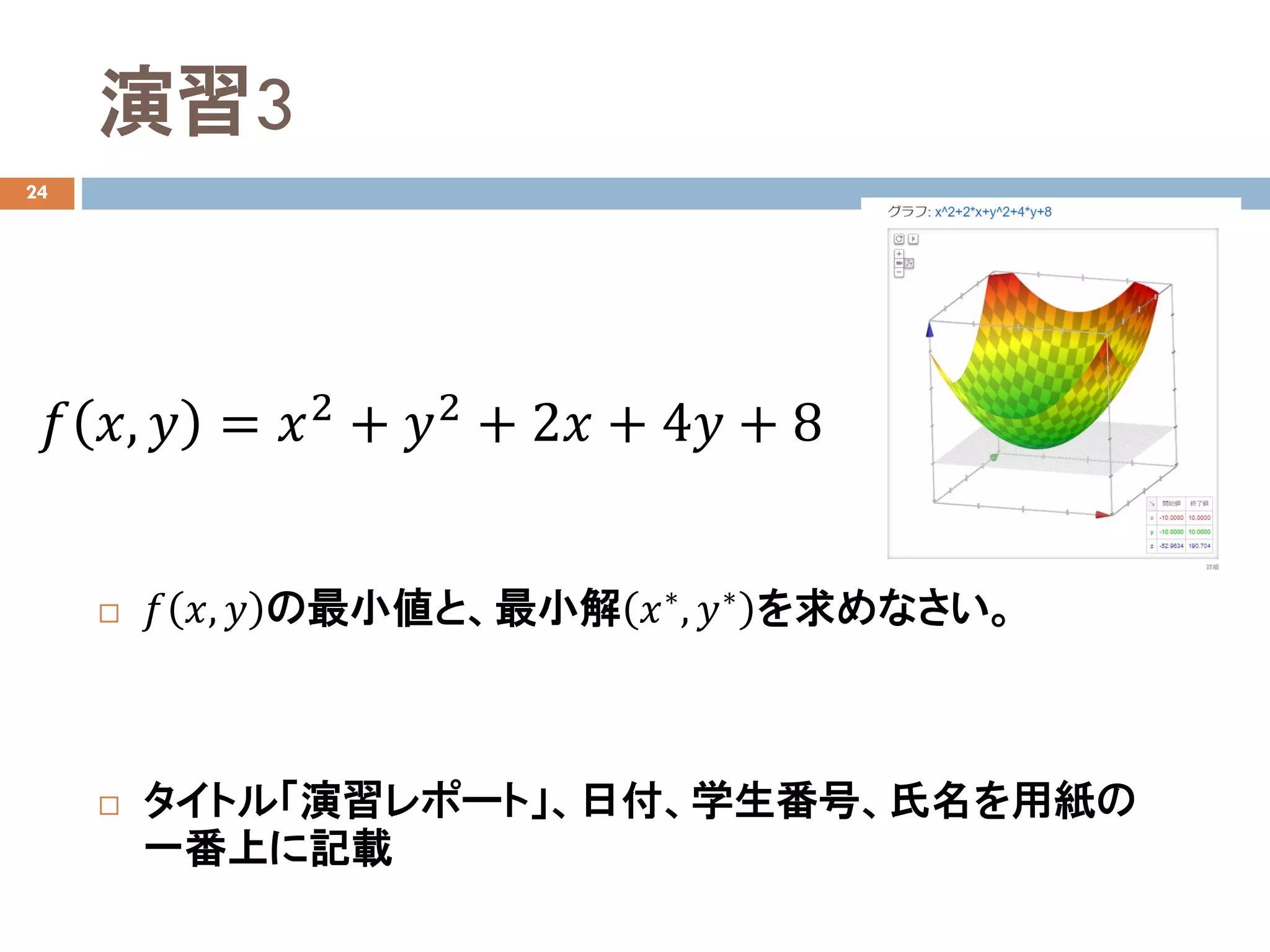
- 16. 演習3 24 𝑓𝑓 𝑥𝑥,𝑦𝑦 の最小値と、最小解 𝑥𝑥∗, 𝑦𝑦∗ を求めなさい。 タイトル「演習レポート」、日付、学生番号、氏名を用紙の 一番上に記載 𝑓𝑓 𝑥𝑥, 𝑦𝑦 = 𝑥𝑥2 + 𝑦𝑦2 + 2𝑥𝑥 + 4𝑦𝑦 + 8
- 17. 内容：最適化手法の復習 26 連立方程式の解法 行列演算を用いた方法 制約なしの最適化問題の解法 微分を用いた方法 偏微分を用いた方法 行列、ベクトルの微分 制約ありの最適化問題の解法 ラグランジュ未定乗数法
- 18. ベクトルに関する微分 27 多変数の関数（ベクトル関数）： 多変数関数を、ベクトル𝒙𝒙に関して微分： ベクトルの各要素に関する𝑓𝑓(𝒙𝒙)の偏微分を、各要素に持つベクトル 𝑓𝑓 𝑥𝑥1, 𝑥𝑥2, 𝑥𝑥2 = 𝑓𝑓(𝒙𝒙) 𝒙𝒙 = 𝑥𝑥1 𝑥𝑥2 𝑥𝑥3 𝛻𝛻𝒙𝒙 𝑓𝑓 𝒙𝒙 = 𝜕𝜕𝑓𝑓(𝒙𝒙) 𝜕𝜕𝒙𝒙 = 𝜕𝜕𝑓𝑓(𝒙𝒙) 𝜕𝜕𝑥𝑥1 𝜕𝜕𝑓𝑓(𝒙𝒙) 𝜕𝜕𝑥𝑥2 𝜕𝜕𝑓𝑓(𝒙𝒙) 𝜕𝜕𝑥𝑥3 𝛻𝛻：ナブラ
- 19. 行列・ベクトルの微分 28 𝑓𝑓 𝒙𝒙= 𝒂𝒂𝚻𝚻 𝒙𝒙の偏微分 𝑓𝑓 𝒙𝒙 = 𝐀𝐀𝒙𝒙の偏微分 𝑓𝑓 𝒙𝒙 = 𝒙𝒙𝚻𝚻 𝐀𝐀𝒙𝒙の偏微分 詳細は、The Matrix Cookbookを参照 𝒂𝒂 = 𝑎𝑎1 𝑎𝑎2 𝑎𝑎3 𝜕𝜕𝑓𝑓(𝒙𝒙) 𝜕𝜕𝒙𝒙 = 𝜕𝜕𝒂𝒂𝚻𝚻 𝒙𝒙 𝜕𝜕𝒙𝒙 = 𝒂𝒂 𝜕𝜕𝑓𝑓(𝒙𝒙) 𝜕𝜕𝒙𝒙 = 𝜕𝜕𝐀𝐀𝒙𝒙 𝜕𝜕𝒙𝒙 = 𝐀𝐀 𝐀𝐀 = 𝑎𝑎11 𝑎𝑎21 𝑎𝑎31 𝑎𝑎12 𝑎𝑎22 𝑎𝑎32 𝑎𝑎13 𝑎𝑎23 𝑎𝑎33 𝒙𝒙 = 𝑥𝑥1 𝑥𝑥2 𝑥𝑥3 𝜕𝜕𝑓𝑓(𝒙𝒙) 𝜕𝜕𝒙𝒙 = 𝜕𝜕𝒙𝒙𝚻𝚻 𝐀𝐀𝒙𝒙 𝜕𝜕𝒙𝒙 = (𝐀𝐀 + 𝐀𝐀𝚻𝚻 )𝒙𝒙 𝐀𝐀が対象の場合： 𝜕𝜕𝒙𝒙𝚻𝚻 𝐀𝐀𝒙𝒙 𝜕𝜕𝒙𝒙 = 2𝐀𝐀𝒙𝒙
- 20. 内容：最適化手法の復習 29 連立方程式の解法 行列演算を用いた方法 制約なしの最適化問題の解法 微分を用いた方法 偏微分を用いた方法 行列、ベクトルの微分 制約ありの最適化問題の解法 ラグランジュ未定乗数法
- 21. 制約あり最適化問題 30 制約あり最適化問題の基本形 最適化問題の例 目的関数（Objectivefunction） min 𝒙𝒙 𝑓𝑓(𝒙𝒙) 制約条件（Constraints） s.t. 𝑔𝑔𝑖𝑖 𝒙𝒙 ∀𝑖𝑖 subject toの略で制約条件 を意味する 全ての𝑖𝑖 = 1,2, … , 𝑛𝑛 を意味する 𝑥𝑥𝑎𝑎 𝑏𝑏 最小値 min 𝑥𝑥 (𝑥𝑥 − 2)2 s.t. 𝑎𝑎 ≤ 𝑥𝑥 ≤ 𝑏𝑏 制約の外
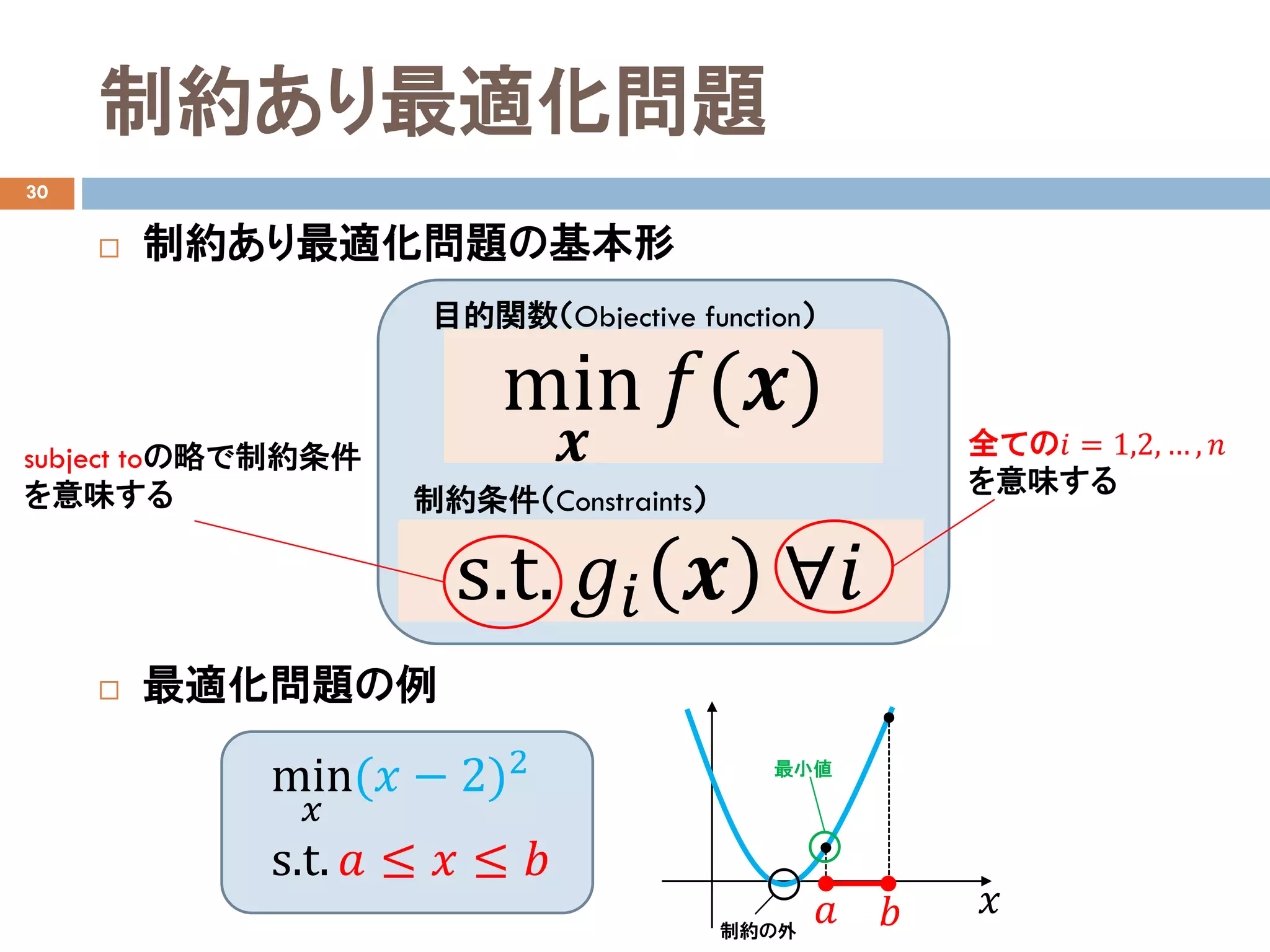
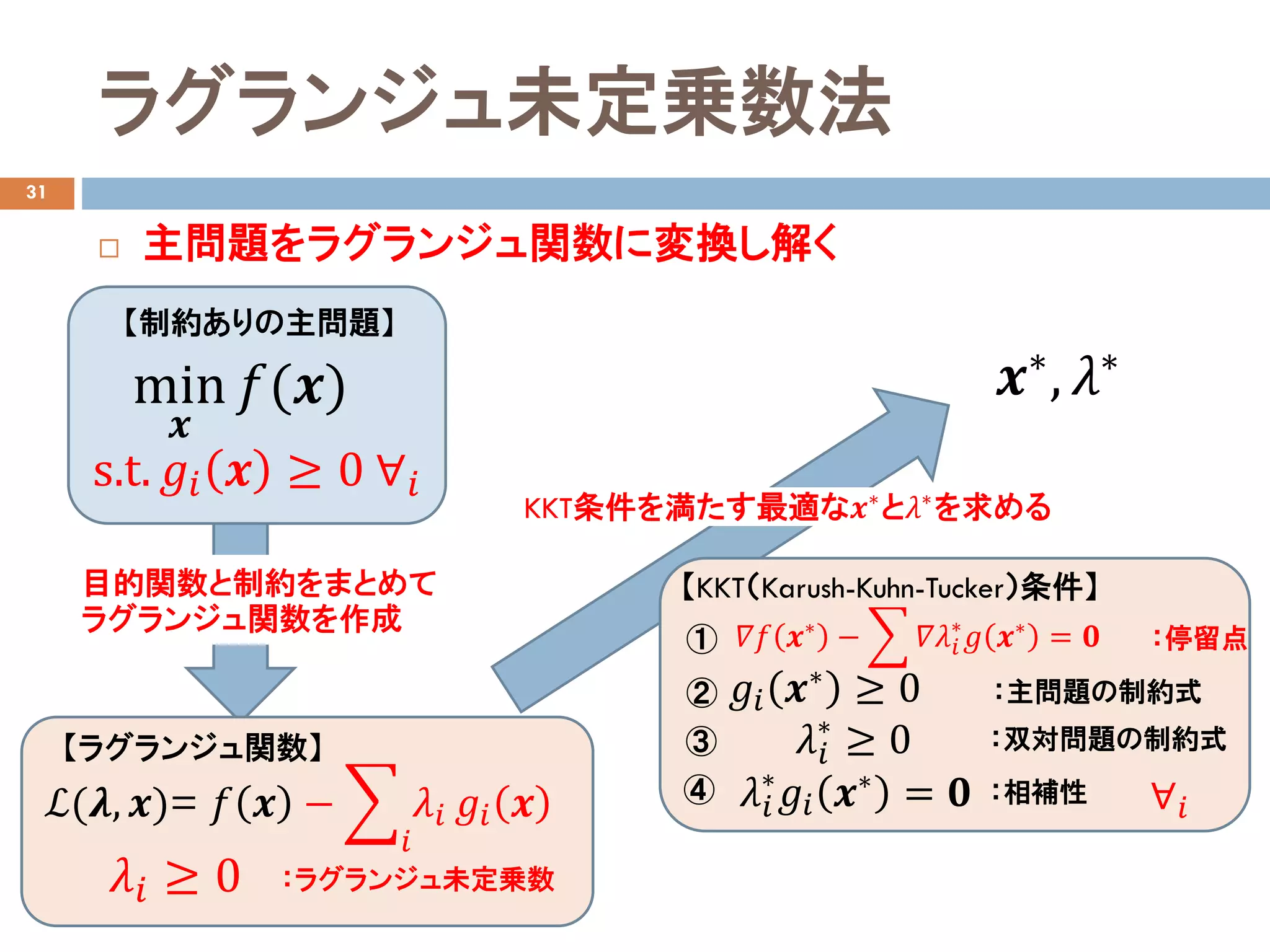
- 22. 主問題をラグランジュ関数に変換し解く ラグランジュ未定乗数法 31 【制約ありの主問題】 min 𝒙𝒙 𝑓𝑓(𝒙𝒙) s.t. 𝑔𝑔𝑖𝑖𝒙𝒙 ≥ 0 ∀𝑖𝑖 【ラグランジュ関数】 ℒ(𝝀𝝀, 𝒙𝒙)= 𝑓𝑓 𝒙𝒙 − � 𝑖𝑖 𝜆𝜆𝑖𝑖 𝑔𝑔𝑖𝑖 𝒙𝒙 𝜆𝜆𝑖𝑖 ≥ 0 ：ラグランジュ未定乗数 目的関数と制約をまとめて ラグランジュ関数を作成 KKT条件を満たす最適な𝒙𝒙∗ と𝜆𝜆∗ を求める 【KKT（Karush-Kuhn-Tucker）条件】 ① ② ③ ④ ：停留点 ：主問題の制約式 ：双対問題の制約式 ：相補性 𝛻𝛻𝑓𝑓 𝒙𝒙∗ − � 𝛻𝛻𝜆𝜆𝑖𝑖 ∗ 𝑔𝑔 𝒙𝒙∗ = 𝟎𝟎 𝑔𝑔𝑖𝑖 𝒙𝒙∗ ≥ 0 𝜆𝜆𝑖𝑖 ∗ ≥ 0 𝜆𝜆𝑖𝑖 ∗ 𝑔𝑔𝑖𝑖 𝒙𝒙∗ = 𝟎𝟎 𝒙𝒙∗ , 𝜆𝜆∗ ∀𝑖𝑖
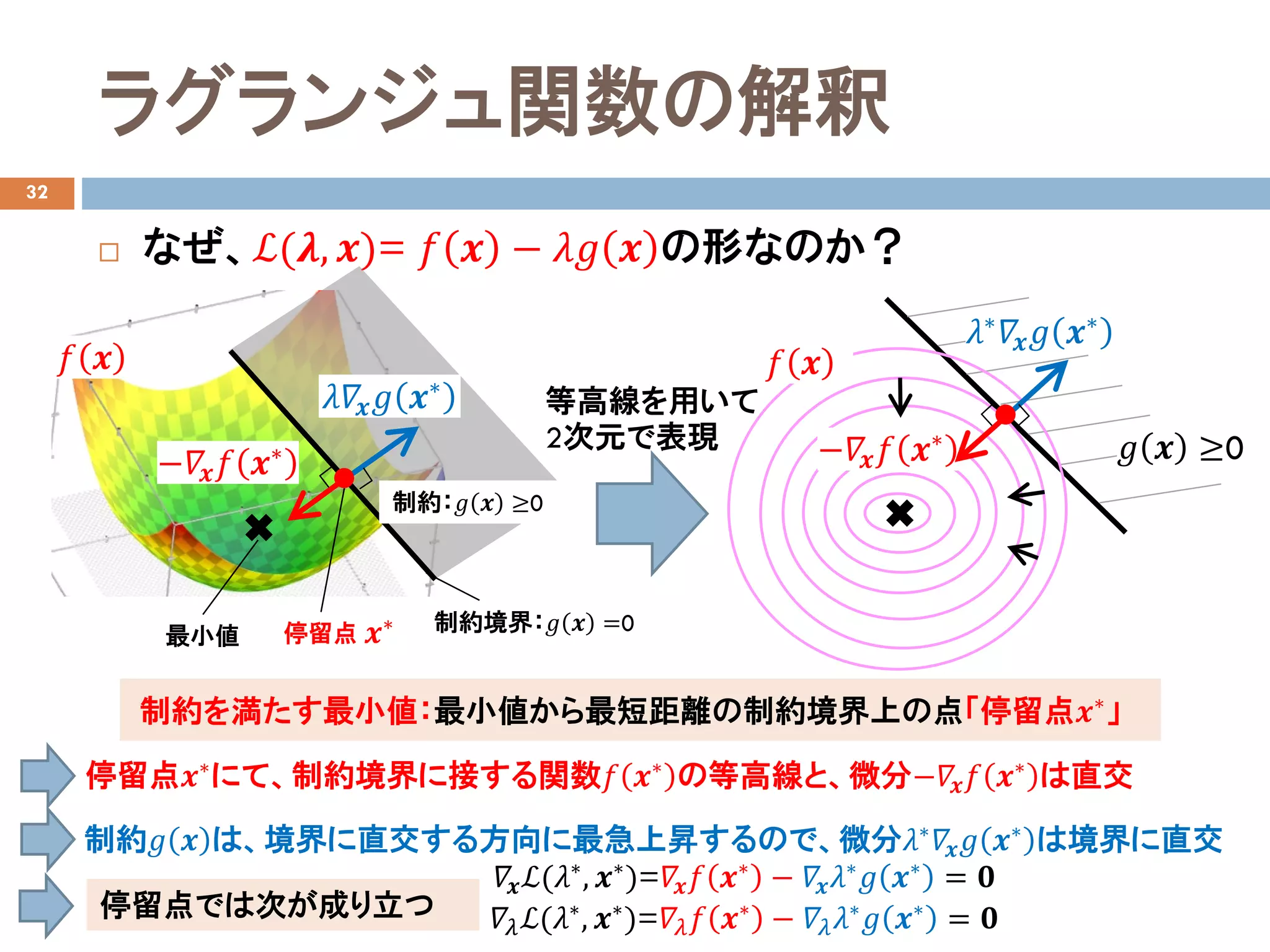
- 23. ラグランジュ関数の解釈 32 なぜ、ℒ(𝝀𝝀, 𝒙𝒙)=𝑓𝑓 𝒙𝒙 − 𝜆𝜆𝑔𝑔 𝒙𝒙 の形なのか？ 𝑓𝑓 𝒙𝒙 最小値 等高線を用いて 2次元で表現 𝜆𝜆𝛻𝛻𝒙𝒙 𝑔𝑔 𝒙𝒙∗ 制約：𝑔𝑔 𝒙𝒙 ≥0 制約境界：𝑔𝑔 𝒙𝒙 =0 −𝛻𝛻𝒙𝒙 𝑓𝑓 𝒙𝒙∗ 停留点 停留点𝒙𝒙∗にて、制約境界に接する関数𝑓𝑓 𝒙𝒙∗ の等高線と、微分−𝛻𝛻𝒙𝒙 𝑓𝑓 𝒙𝒙∗ は直交 制約𝑔𝑔 𝒙𝒙 は、境界に直交する方向に最急上昇するので、微分𝜆𝜆∗ 𝛻𝛻𝒙𝒙 𝑔𝑔 𝒙𝒙∗ は境界に直交 停留点では次が成り立つ 𝒙𝒙∗ 𝛻𝛻𝒙𝒙ℒ(𝜆𝜆∗, 𝒙𝒙∗)=𝛻𝛻𝒙𝒙 𝑓𝑓 𝒙𝒙∗ − 𝛻𝛻𝒙𝒙 𝜆𝜆∗ 𝑔𝑔 𝒙𝒙∗ = 𝟎𝟎 𝛻𝛻𝜆𝜆ℒ(𝜆𝜆∗, 𝒙𝒙∗)=𝛻𝛻𝜆𝜆 𝑓𝑓 𝒙𝒙∗ − 𝛻𝛻𝜆𝜆 𝜆𝜆∗ 𝑔𝑔 𝒙𝒙∗ = 𝟎𝟎 𝑔𝑔 𝒙𝒙 ≥0−𝛻𝛻𝒙𝒙 𝑓𝑓 𝒙𝒙∗ 𝑓𝑓 𝒙𝒙 𝜆𝜆∗ 𝛻𝛻𝒙𝒙 𝑔𝑔 𝒙𝒙∗ 制約を満たす最小値：最小値から最短距離の制約境界上の点「停留点𝒙𝒙∗ 」
- 24. ラグランジュ未定乗数法の例 33 ラグランジュ関数を求める 偏微分して0と置く min 𝑥𝑥,𝑦𝑦,𝑧𝑧 𝑥𝑥2+ 𝑦𝑦2 + 𝑧𝑧2 s.t. 𝑥𝑥 + 𝑦𝑦 + 𝑧𝑧 = 1 ℒ(𝜆𝜆, 𝑥𝑥, 𝑦𝑦, 𝑧𝑧)=𝑥𝑥2 + 𝑦𝑦2 + 𝑧𝑧2 − 𝜆𝜆(𝑥𝑥 + 𝑦𝑦 + 𝑧𝑧 − 1) 𝜆𝜆 ≥ 0 𝜕𝜕ℒ 𝜕𝜕𝑥𝑥 = 2𝑥𝑥 − 𝜆𝜆 = 0 𝜕𝜕ℒ 𝜕𝜕𝑦𝑦 = 2𝑦𝑦 − 𝜆𝜆 = 0 主問題： 𝜕𝜕ℒ 𝜕𝜕𝑧𝑧 = 2𝑧𝑧 − 𝜆𝜆 = 0 −𝑥𝑥 − 𝑦𝑦 − 𝑧𝑧 + 1= − 3 2 𝜆𝜆 + 1 = 0 𝜕𝜕ℒ 𝜕𝜕𝜆𝜆 = −𝑥𝑥 − 𝑦𝑦 − 𝑧𝑧 + 1=0 𝑥𝑥 = 𝑦𝑦 = 𝑧𝑧 = 1 2 𝜆𝜆 ∴ 𝜆𝜆∗ = 2 3 ∴ 𝑥𝑥∗ = 𝑦𝑦∗ = 𝑧𝑧∗ = 1 3
- 25. 演習4 34 最適解𝑥𝑥∗と𝑦𝑦∗を求めなさい。 タイトル「演習レポート」、日付、学生番号、氏名を用紙の 一番上に記載 min 𝑥𝑥,𝑦𝑦 𝑥𝑥2 +𝑦𝑦2 s.t. 𝑥𝑥 + 𝑦𝑦 = 1 主問題：
- 26. 課題 36 1. 𝑥𝑥2 +𝑦𝑦2 = 1の制約条件のもとで、 𝑦𝑦𝑧𝑧 + 𝑥𝑥𝑥𝑥の最大値を求めなさい。 2. 𝑥𝑥2 + 𝑦𝑦2 = 2と𝑥𝑥𝑥𝑥 = 1の制約条件のもとで、𝑥𝑥 + 𝑦𝑦の最大値と 最小値を求めなさい。 3. 𝒙𝒙𝚻𝚻 𝒙𝒙 = 1の制約条件のもとで、2次形式𝒙𝒙𝚻𝚻 𝐀𝐀𝒙𝒙の最大化問題が、 以下の制約付きの固有値問題になることを証明しなさい。 𝐀𝐀𝒙𝒙 = 𝝀𝝀𝒙𝒙 s.t. 𝒙𝒙𝚻𝚻 𝒙𝒙 = 1
- 27. レポートの提出方法 37 演習レポート： タイトル「演習レポート」、日付・学生番号・氏名を用紙の一番上に記載 課題レポート ： タイトル「課題レポート」、出題日・学生番号・氏名を用紙の一番上に記載 2ページ以上になる場合は、ホッチキス留め A4サイズの用紙を使用 一度に複数の課題レポートを提出する場合出題日ごとに別々に綴じる