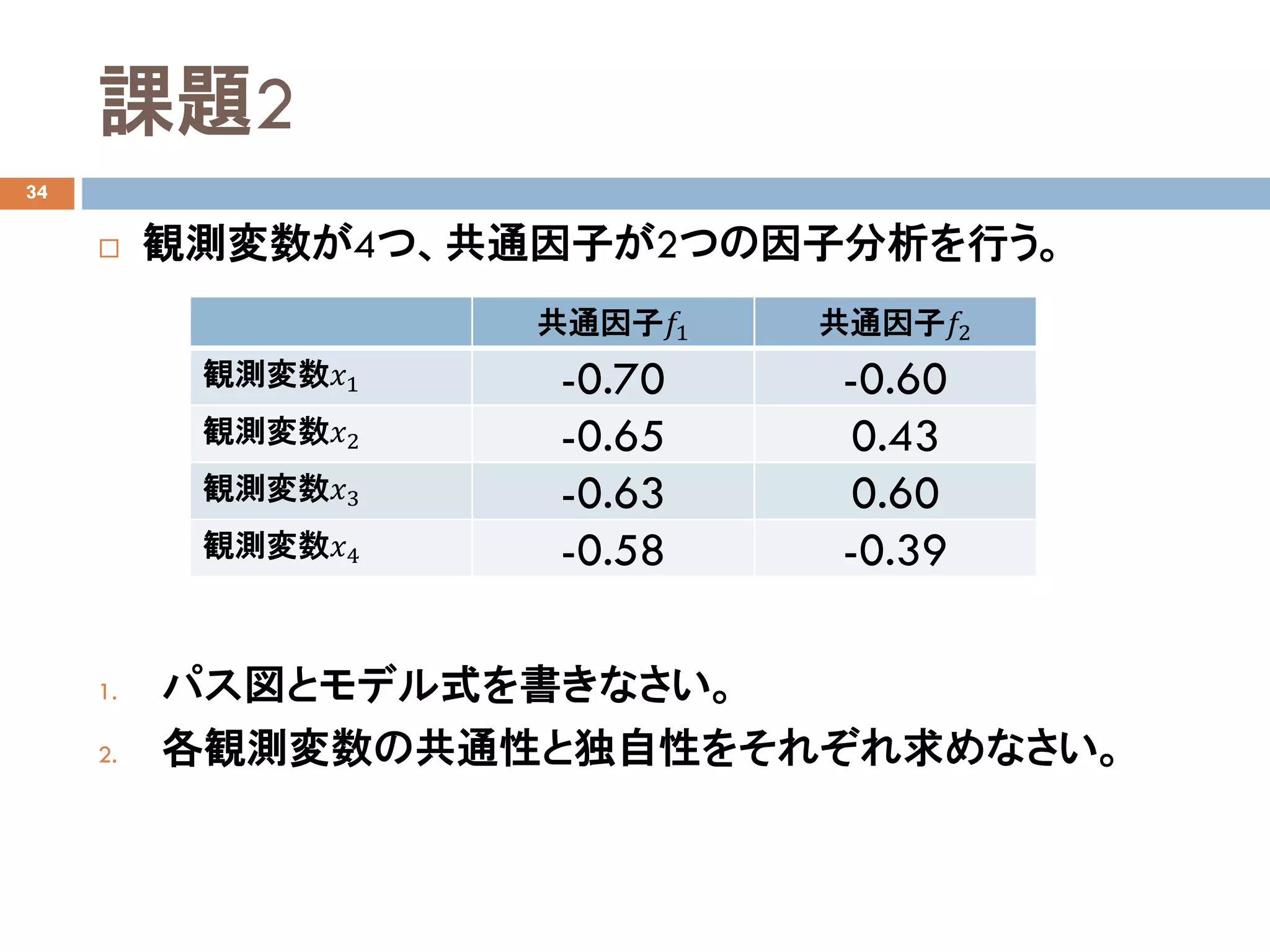
More Related Content
PPTX
PDF
PDF
PDF
PPTX
PDF
PDF
Word Tour: One-dimensional Word Embeddings via the Traveling Salesman Problem... PDF
状態空間モデルの考え方・使い方 - TokyoR #38 What's hot
PDF
PDF
深層学習の不確実性 - Uncertainty in Deep Neural Networks - PDF
PDF
PDF
PDF
PDF
PDF
PPTX
Maximum Entropy IRL(最大エントロピー逆強化学習)とその発展系について PDF
ゼロから始める深層強化学習(NLP2018講演資料)/ Introduction of Deep Reinforcement Learning PDF
PDF
PDF
PDF
PDF
Recent Advances on Transfer Learning and Related Topics Ver.2 PDF
Granger因果による�時系列データの因果推定(因果フェス2015) PDF
PPTX
PDF
PDF
Similar to データ解析10 因子分析の基礎
PDF
PPTX
PDF
PDF
PDF
PDF
PDF
PPT
PDF
PDF
PPTX
PDF
PDF
PPTX
PDF
PDF
PDF
KEY
第5章 統計的仮説検定 (Rによるやさしい統計学) PDF
PDF
More from Hirotaka Hachiya
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
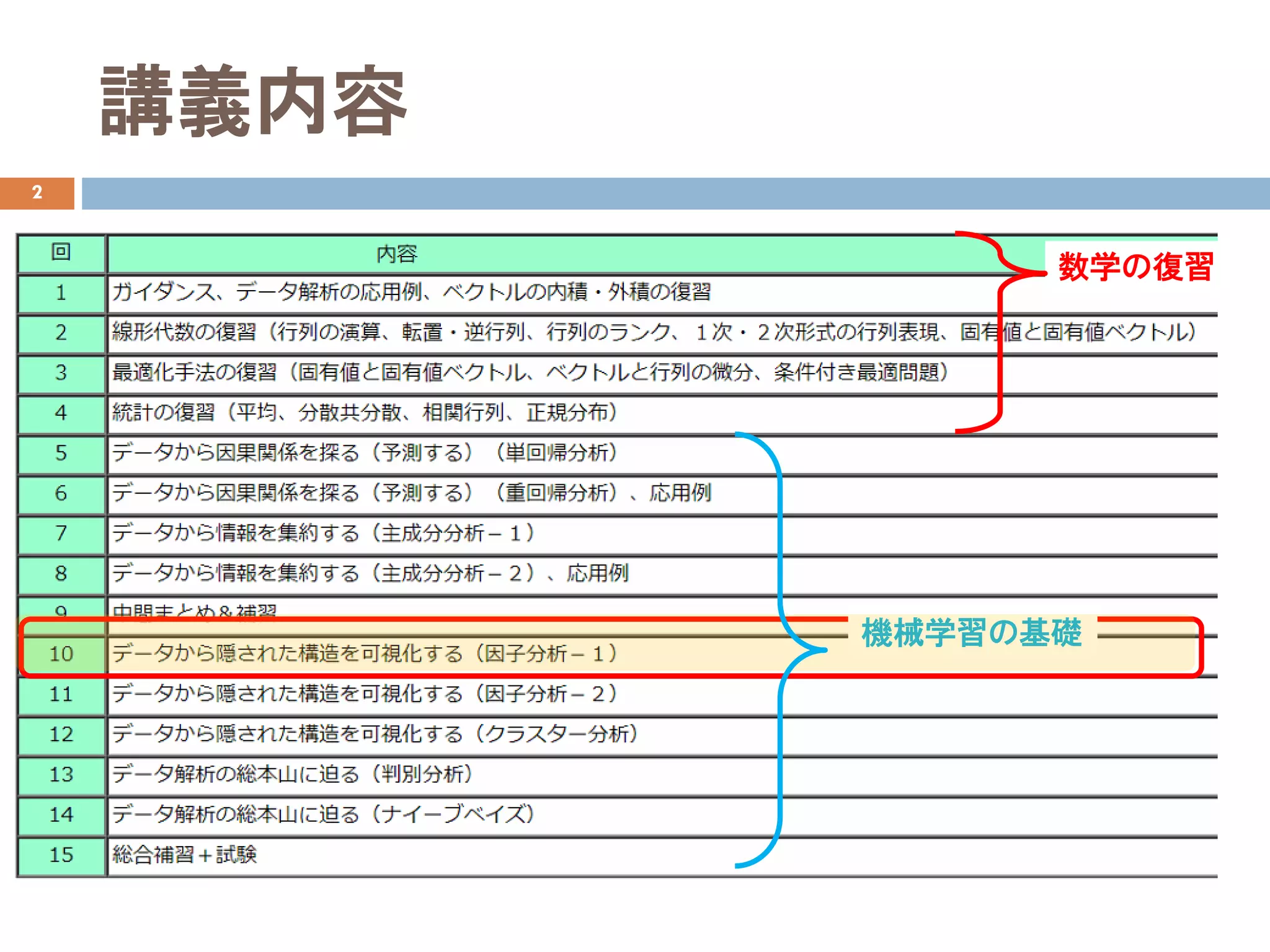
データ解析10 因子分析の基礎
- 1.
- 2.
- 3.
- 4.
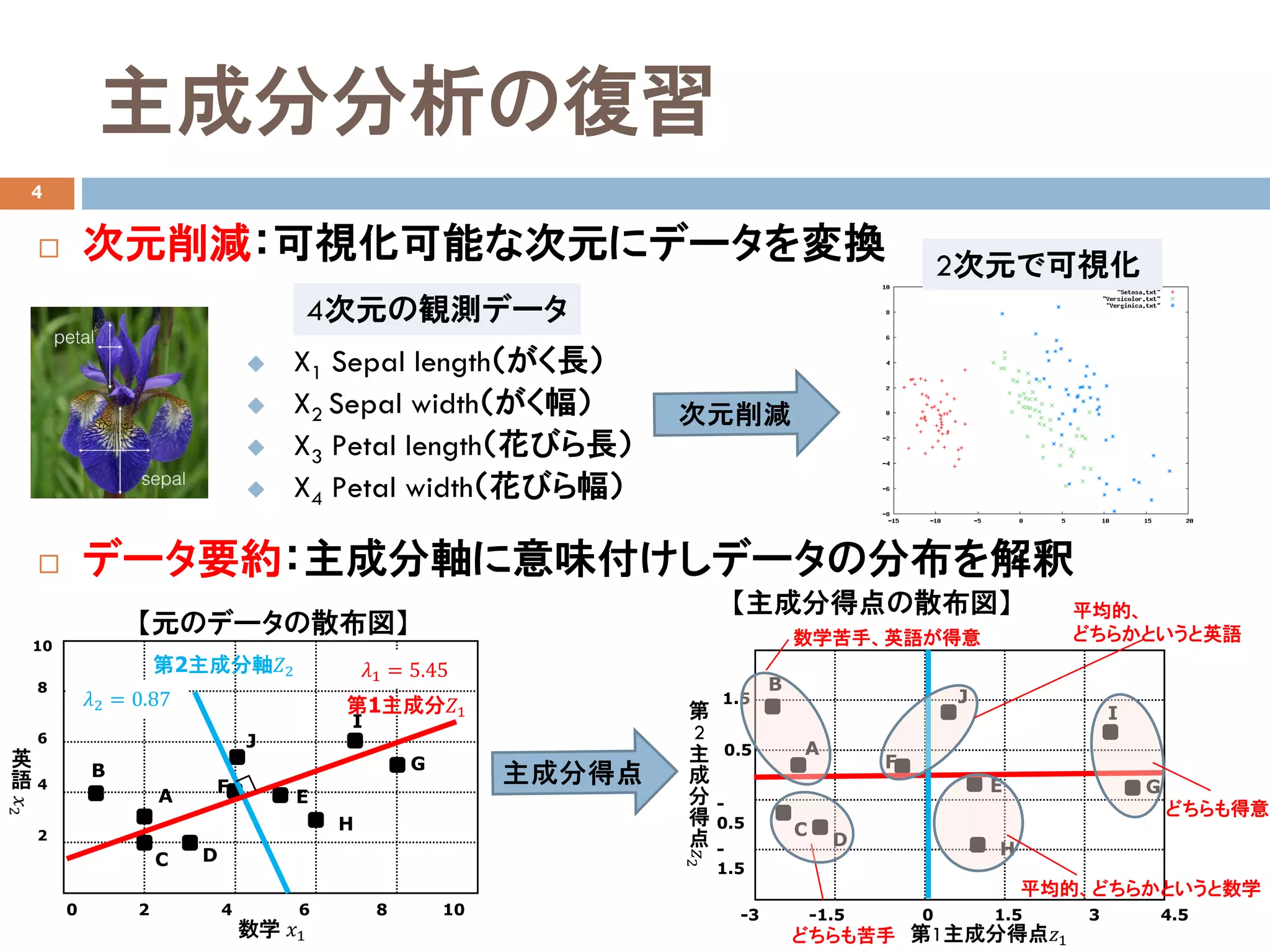
主成分分析の復習
4
次元削減:可視化可能な次元にデータを変換
データ要約:主成分軸に意味付けしデータの分布を解釈
X1 Sepal length(がく長)
X2 Sepal width(がく幅)
X3 Petal length(花びら長)
X4 Petal width(花びら幅)
4次元の観測データ
2次元で可視化
英
語
A
B
C D
E
F
H
G
J
I
0 2 4 6 8 10
10
8
6
4
2
数学 𝑥𝑥1
第2主成分軸𝑍𝑍2
第1主成分𝑍𝑍1
𝜆𝜆1 = 5.45
𝜆𝜆2 = 0.87
【元のデータの散布図】
第
2主
成
分
得
点
-3 -1.5 0 1.5 3 4.5
B
A
C
D
E
F
G
H
第1主成分得点𝑧𝑧1
I
J
-
1.5
1.5
-
0.5
0.5
【主成分得点の散布図】
どちらも苦手
平均的、
どちらかというと英語
平均的、どちらかというと数学
どちらも得意
数学苦手、英語が得意
- 5.
- 6.
- 7.
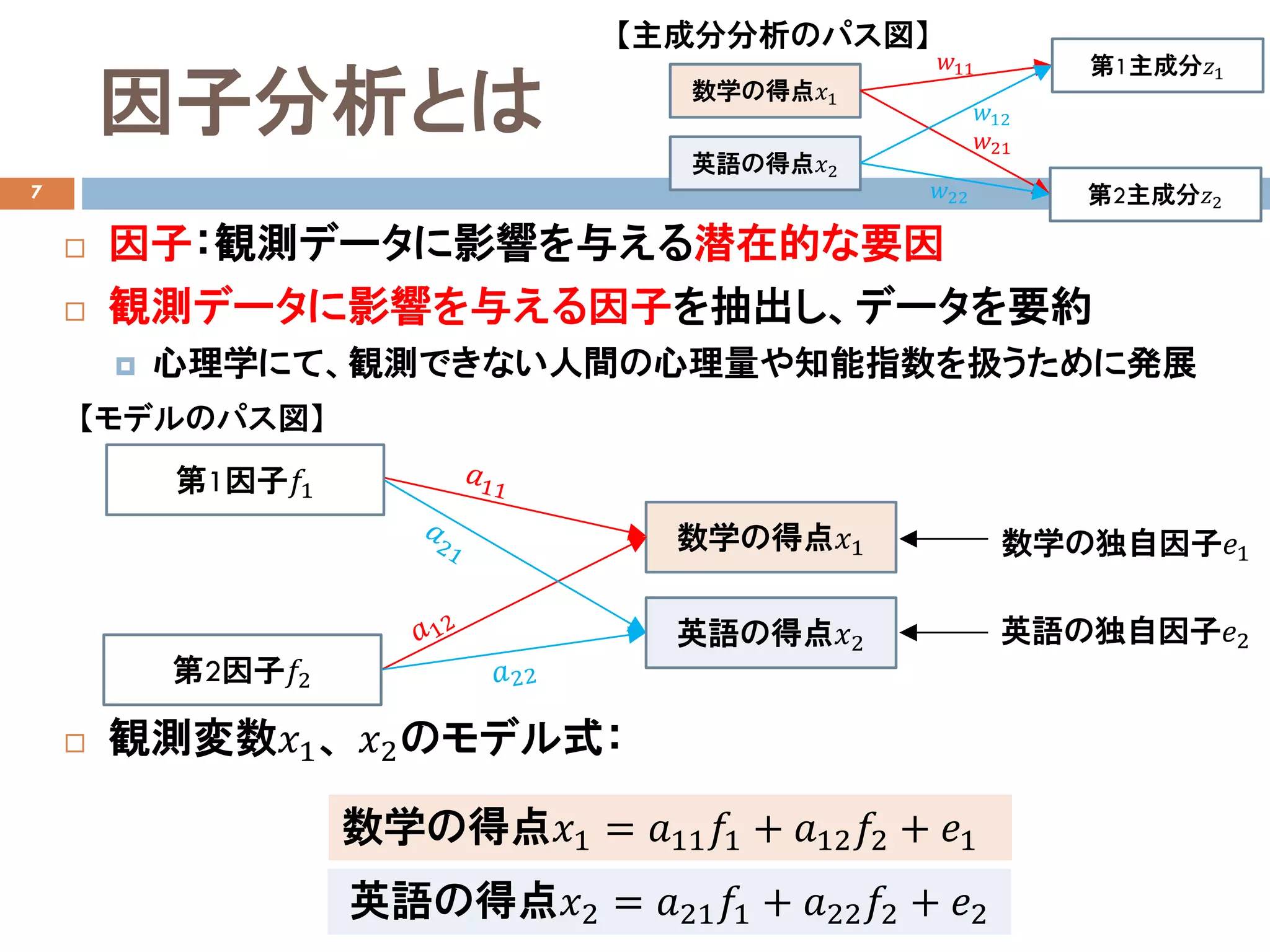
因子分析とは
7
因子:観測データに影響を与える潜在的な要因
観測データに影響を与える因子を抽出し、データを要約
心理学にて、観測できない人間の心理量や知能指数を扱うために発展
観測変数𝑥𝑥1、 𝑥𝑥2のモデル式:
数学の得点𝑥𝑥1
英語の得点𝑥𝑥2
第1因子𝑓𝑓1
第2因子𝑓𝑓2
数学の得点𝑥𝑥1 = 𝑎𝑎11 𝑓𝑓1 + 𝑎𝑎12 𝑓𝑓2 + 𝑒𝑒1
英語の得点𝑥𝑥2 = 𝑎𝑎21 𝑓𝑓1 + 𝑎𝑎22 𝑓𝑓2 + 𝑒𝑒2
数学の独自因子𝑒𝑒1
英語の独自因子𝑒𝑒2
【モデルのパス図】
数学の得点𝑥𝑥1
英語の得点𝑥𝑥2
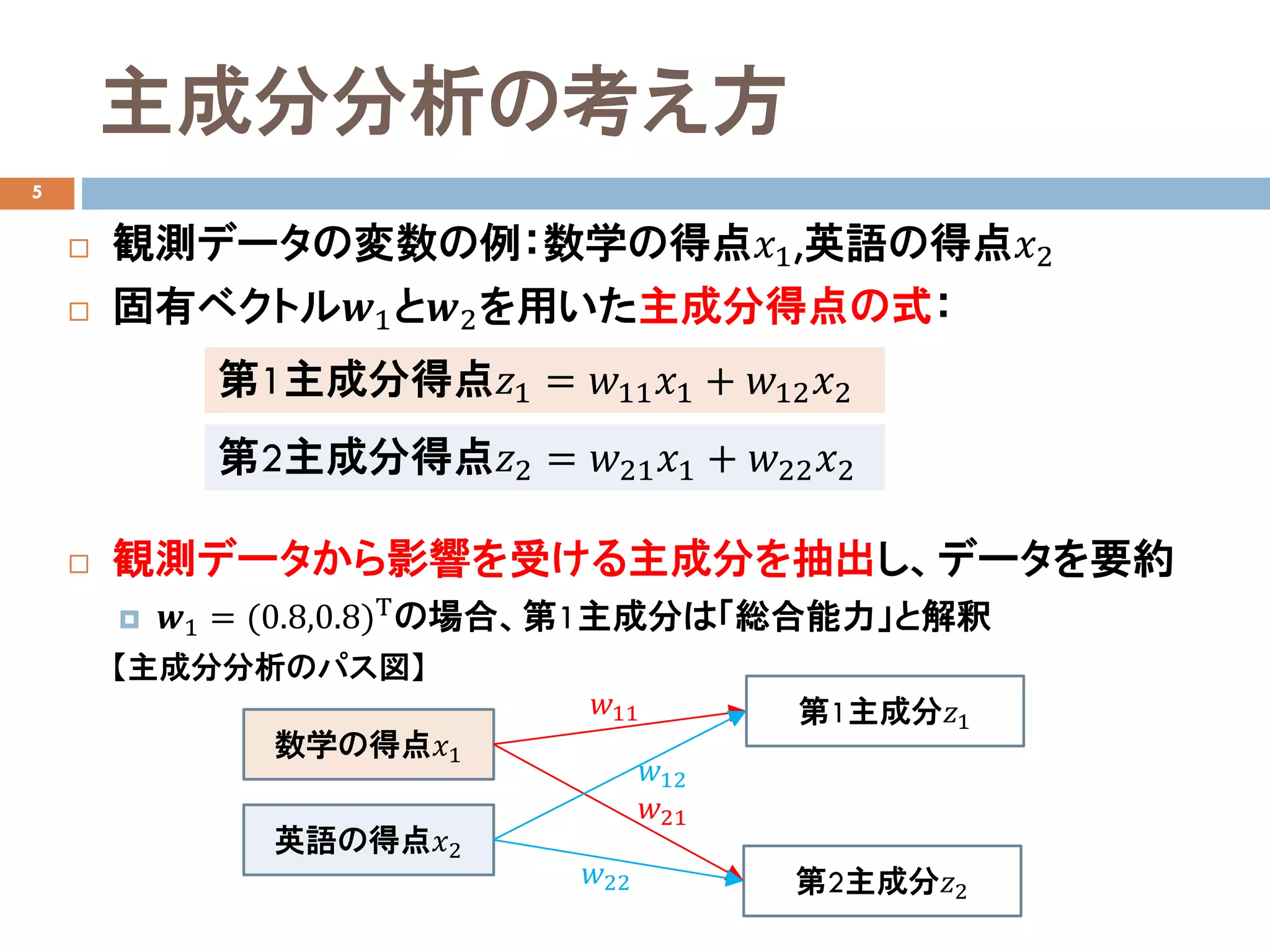
第1主成分𝑧𝑧1
第2主成分𝑧𝑧2
𝑤𝑤11
𝑤𝑤21
𝑤𝑤12
𝑤𝑤22
【主成分分析のパス図】
- 8.
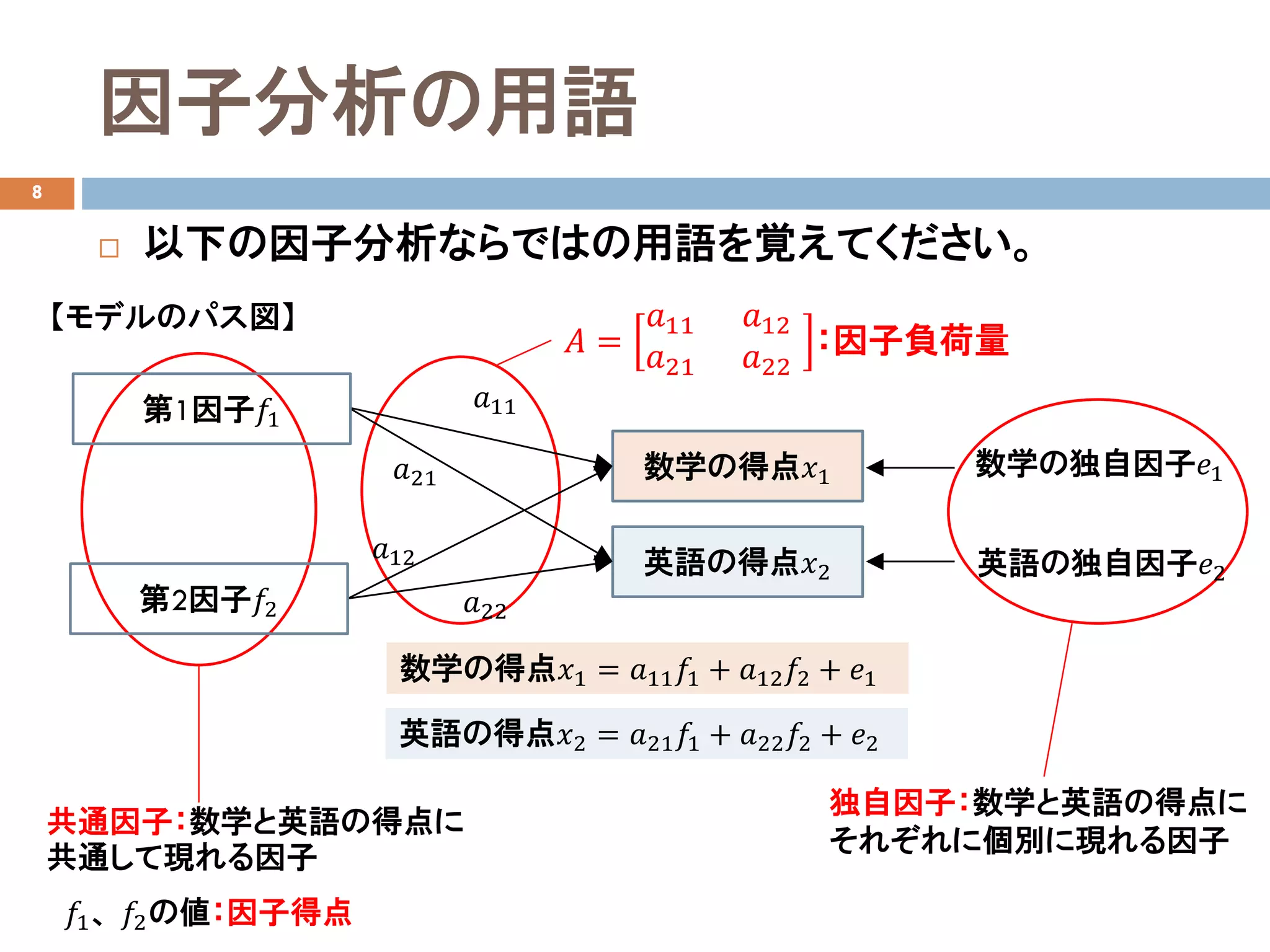
因子分析の用語
8
数学の得点𝑥𝑥1 = 𝑎𝑎11𝑓𝑓1 + 𝑎𝑎12 𝑓𝑓2 + 𝑒𝑒1
英語の得点𝑥𝑥2 = 𝑎𝑎21 𝑓𝑓1 + 𝑎𝑎22 𝑓𝑓2 + 𝑒𝑒2
𝐴𝐴 =
𝑎𝑎11 𝑎𝑎12
𝑎𝑎21 𝑎𝑎22
:因子負荷量
共通因子:数学と英語の得点に
共通して現れる因子
以下の因子分析ならではの用語を覚えてください。
独自因子:数学と英語の得点に
それぞれに個別に現れる因子
𝑓𝑓1、 𝑓𝑓2の値:因子得点
数学の得点𝑥𝑥1
英語の得点𝑥𝑥2
𝑎𝑎11
𝑎𝑎21
𝑎𝑎12
𝑎𝑎22
第1因子𝑓𝑓1
第2因子𝑓𝑓2
数学の独自因子𝑒𝑒1
英語の独自因子𝑒𝑒2
【モデルのパス図】
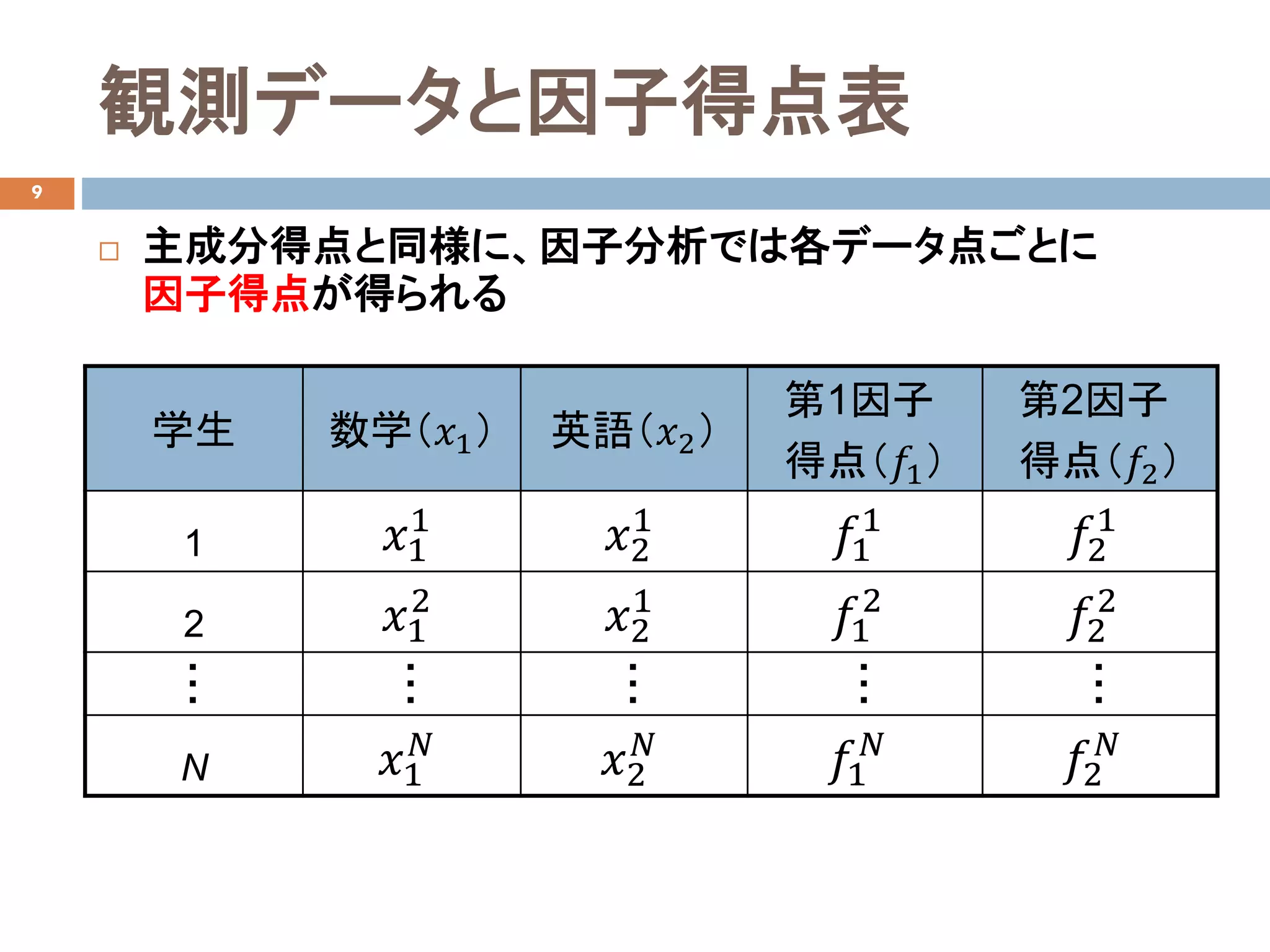
- 9.
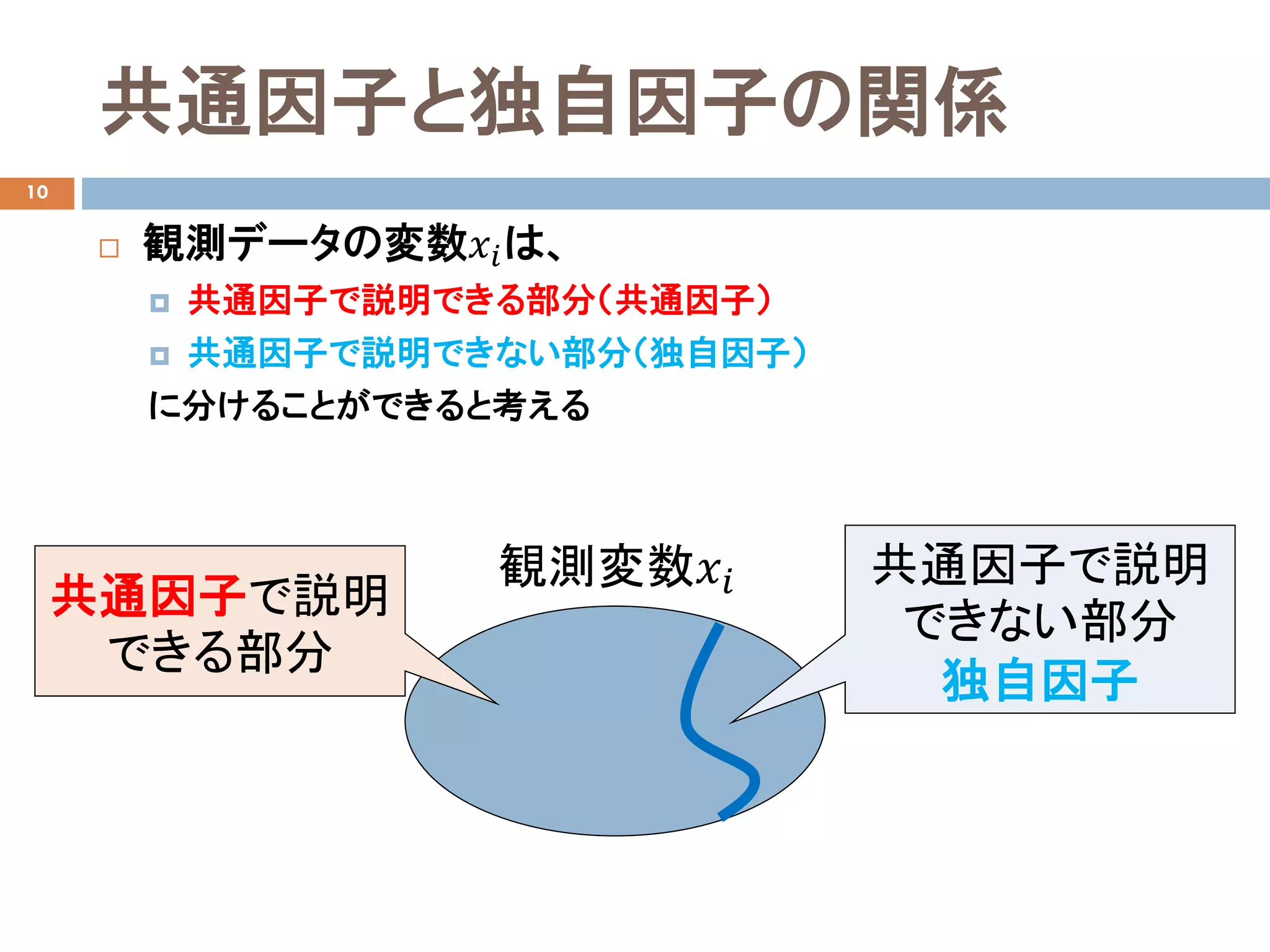
- 10.
- 11.
- 12.
- 13.
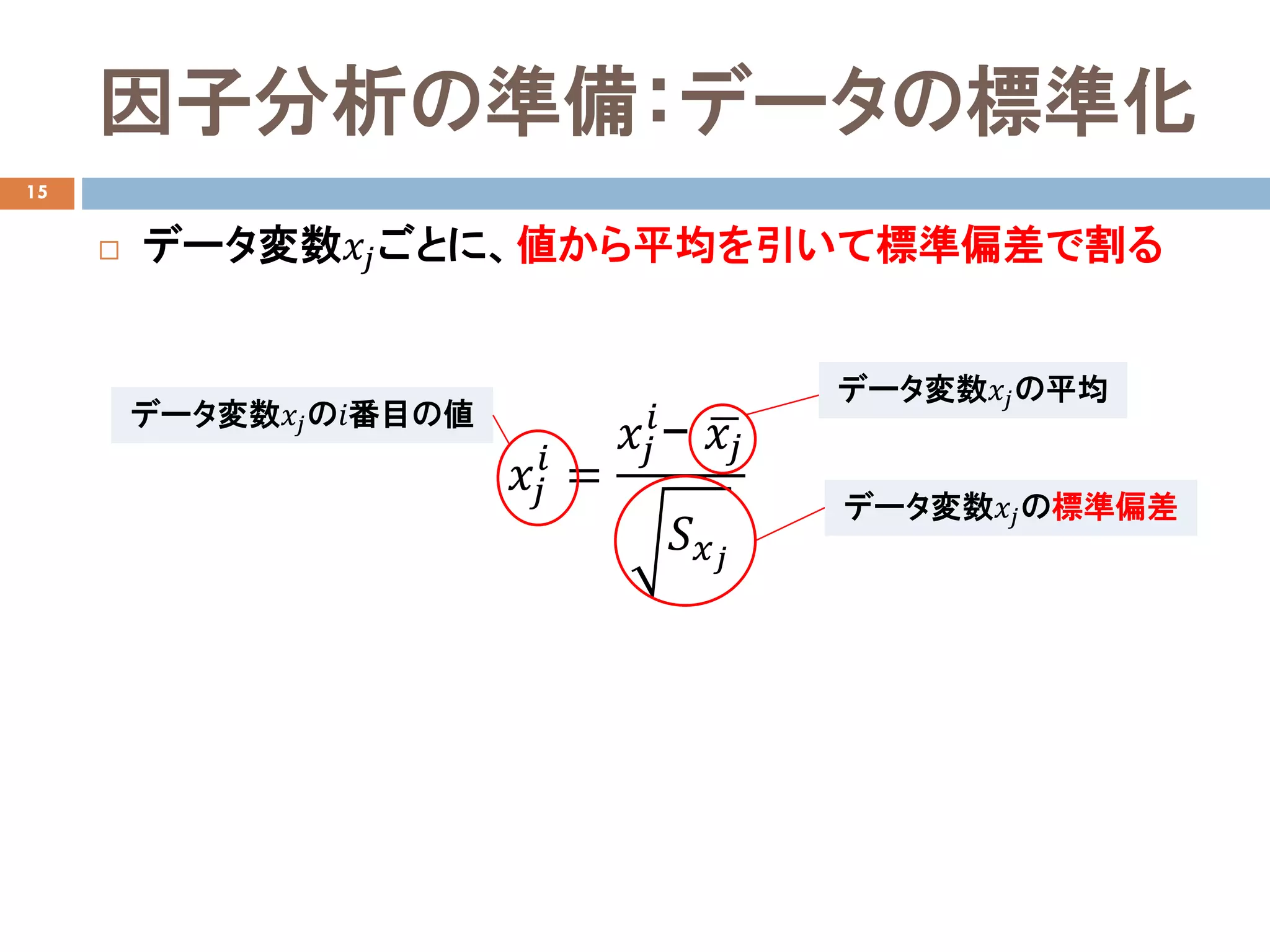
- 14.
因子分析の準備:因子の条件
16
共通因子𝑓𝑓1、 𝑓𝑓2は標準化されている
独自因子𝑒𝑒1、𝑒𝑒2の平均は0である
因子は、どの2つをとっても共分散は0(独自)
教科書p201を参照
𝐸𝐸 𝑓𝑓1 = 𝐸𝐸 𝑓𝑓2 = 0 𝑉𝑉𝑉𝑉𝑉𝑉 𝑓𝑓1 = 𝑉𝑉𝑉𝑉𝑉𝑉 𝑓𝑓2 = 1
𝐸𝐸 𝑒𝑒1 = 𝐸𝐸 𝑒𝑒1 = 0
𝐶𝐶𝐶𝐶𝐶𝐶 𝑓𝑓1, 𝑒𝑒1 = 𝐶𝐶𝐶𝐶𝐶𝐶 𝑓𝑓1, 𝑒𝑒2 = 𝐶𝐶𝐶𝐶𝐶𝐶 𝑓𝑓2, 𝑒𝑒1 = 𝐶𝐶𝐶𝐶𝐶𝐶 𝑓𝑓2, 𝑒𝑒2 = 0
𝐶𝐶𝐶𝐶𝐶𝐶 𝑒𝑒1, 𝑒𝑒2 = 𝐶𝐶𝐶𝐶𝐶𝐶 𝑒𝑒2, 𝑒𝑒1 = 0
- 15.
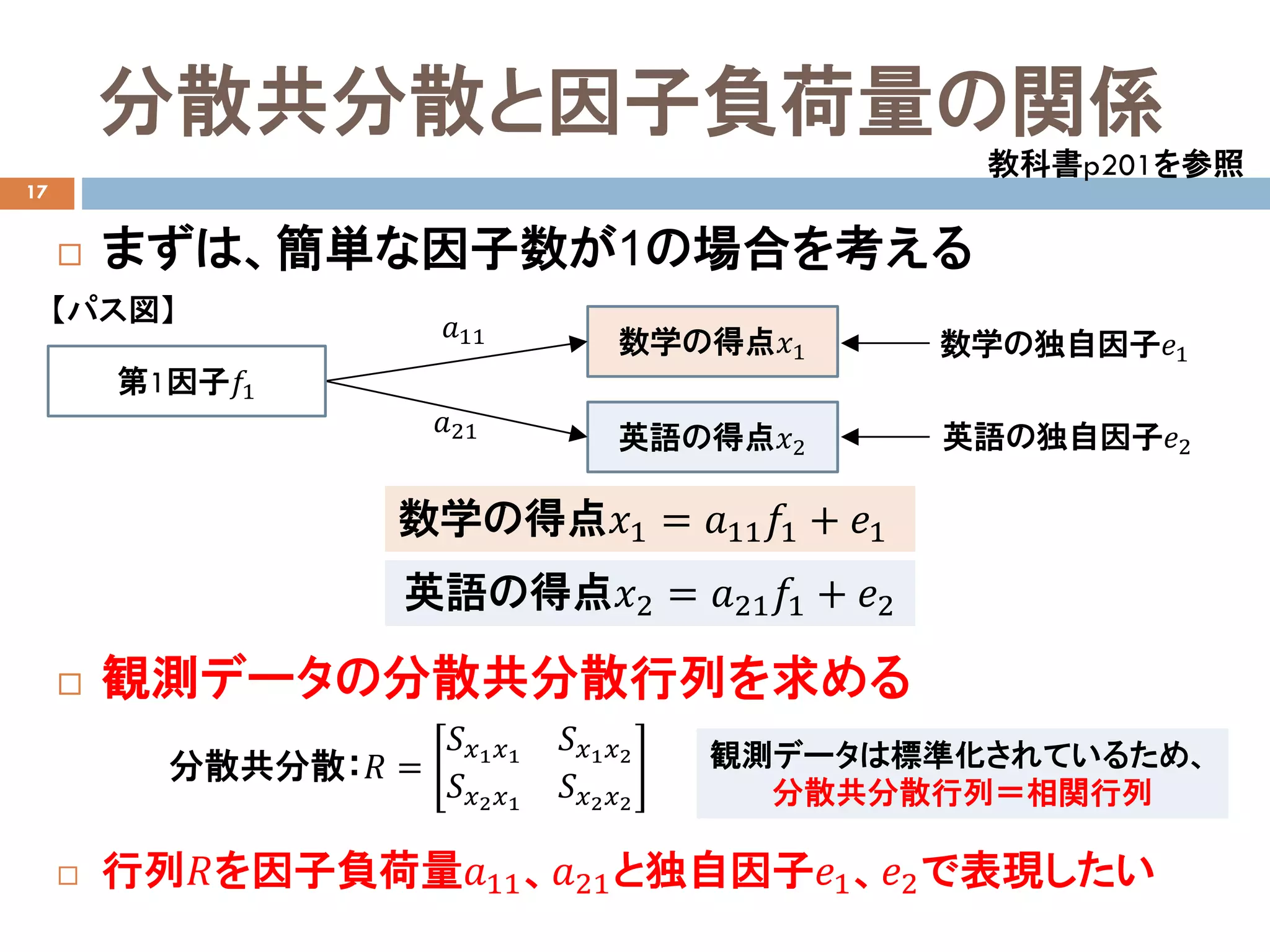
分散共分散と因子負荷量の関係
17
まずは、簡単な因子数が1の場合を考える
観測データの分散共分散行列を求める
行列𝑅𝑅を因子負荷量𝑎𝑎11、𝑎𝑎21と独自因子𝑒𝑒1、𝑒𝑒2で表現したい
教科書p201を参照
分散共分散:𝑅𝑅 =
𝑆𝑆𝑥𝑥1 𝑥𝑥1
𝑆𝑆𝑥𝑥1 𝑥𝑥2
𝑆𝑆𝑥𝑥2 𝑥𝑥1
𝑆𝑆𝑥𝑥2 𝑥𝑥2
数学の得点𝑥𝑥1
英語の得点𝑥𝑥2
𝑎𝑎11
𝑎𝑎21
第1因子𝑓𝑓1
数学の独自因子𝑒𝑒1
英語の独自因子𝑒𝑒2
【パス図】
数学の得点𝑥𝑥1 = 𝑎𝑎11 𝑓𝑓1 + 𝑒𝑒1
英語の得点𝑥𝑥2 = 𝑎𝑎21 𝑓𝑓1 + 𝑒𝑒2
観測データは標準化されているため、
分散共分散行列=相関行列
- 16.
- 17.
分散共分散と因子負荷量の関係2
21
分散共分散行列と因子負荷量との関係式の行列表現
関係式は、任意の数の観測変数と因子に対して成り立つ
観測変数が3、因子数が1つの場合:
観測変数が2、因子数が2つの場合:
𝑅𝑅 =
𝑆𝑆𝑥𝑥1 𝑥𝑥1
𝑆𝑆𝑥𝑥1 𝑥𝑥2
𝑆𝑆𝑥𝑥2 𝑥𝑥1
𝑆𝑆𝑥𝑥2 𝑥𝑥2
=
𝑎𝑎11 𝑎𝑎11 𝑎𝑎11 𝑎𝑎21
𝑎𝑎21 𝑎𝑎11 𝑎𝑎21 𝑎𝑎21
+
Var(𝑒𝑒1)
0
0
Var(𝑒𝑒2)
=
𝑎𝑎11
𝑎𝑎21
𝑎𝑎11 𝑎𝑎21 +
Var(𝑒𝑒1)
0
0
Var(𝑒𝑒2)
= 𝐴𝐴𝐴𝐴Τ + 𝐸𝐸
𝐴𝐴 =
𝑎𝑎11
𝑎𝑎21
𝑎𝑎31
𝐴𝐴 =
𝑎𝑎11
𝑎𝑎21
𝑎𝑎12
𝑎𝑎22
𝐸𝐸 =
Var(𝑒𝑒1)
0
0
0
Var(𝑒𝑒2)
0
0
0
Var(𝑒𝑒3)
𝐸𝐸 =
Var(𝑒𝑒1)
0
0
Var(𝑒𝑒2)
𝑆𝑆𝑥𝑥1 𝑥𝑥1
= 𝑎𝑎11 𝑎𝑎11 + Var(𝑒𝑒1) 𝑆𝑆𝑥𝑥1 𝑥𝑥2
= 𝑎𝑎11 𝑎𝑎21
- 18.
- 19.
因子負荷量を求める例(因子数=1)
23
3変数(数学𝑥𝑥1、国語𝑥𝑥2、理科𝑥𝑥3)観測データの共分散の値が
𝑆𝑆𝑥𝑥1 𝑥𝑥2
=0.72、𝑆𝑆𝑥𝑥2 𝑥𝑥3
= 0.56、𝑆𝑆𝑥𝑥3 𝑥𝑥1
= 0.63の場合を考える
①分散共分散と因子負荷量の関係式より連立方程式を作る
𝑅𝑅 =
1
0.72
0.63
0.72
1
0.56
0.63
0.56
1
= 𝐴𝐴𝐴𝐴Τ + 𝐸𝐸
=
𝑎𝑎11 𝑎𝑎11 + Var(𝑒𝑒1)
𝑎𝑎21 𝑎𝑎11
𝑎𝑎31 𝑎𝑎11
𝑎𝑎11 𝑎𝑎21
𝑎𝑎21 𝑎𝑎21 + Var(𝑒𝑒2)
𝑎𝑎31 𝑎𝑎21
𝑎𝑎11 𝑎𝑎31
𝑎𝑎21 𝑎𝑎31
𝑎𝑎31 𝑎𝑎31 + Var(𝑒𝑒3)
教科書p201を参照
𝑎𝑎11 𝑎𝑎11 + Var(𝑒𝑒1) = 𝑎𝑎21 𝑎𝑎21 + Var(𝑒𝑒2) = 𝑎𝑎31 𝑎𝑎31 + Var(𝑒𝑒3) = 1
𝑎𝑎21 𝑎𝑎11 = 0.72 𝑎𝑎31 𝑎𝑎11 = 0.63 𝑎𝑎21 𝑎𝑎31 = 0.56
- 20.
因子負荷量を求める例(因子数=1) 2
24
②連立方程式から因子負荷量を求める
③求めた共通因子を方程式に代入し独自因子の分散を求める
教科書p201を参照
𝑎𝑎11 𝑎𝑎11=
𝑎𝑎21 𝑎𝑎11 𝑎𝑎31 𝑎𝑎11
𝑎𝑎21 𝑎𝑎31
=
0.72 0.63
0.56
= 0.81 𝑎𝑎11 = 0.9
𝑎𝑎21 =
𝑎𝑎21 𝑎𝑎11
𝑎𝑎11
=
0.72
0.9
= 0.8 𝑎𝑎31 =
𝑎𝑎31 𝑎𝑎11
𝑎𝑎11
=
0.63
0.9
= 0.7
Var 𝑒𝑒1 = 0.19
Var 𝑒𝑒2 = 0.36
Var 𝑒𝑒3 = 0.51
0.81 + Var 𝑒𝑒1 = 1
0.64 + Var 𝑒𝑒2 = 1
0.49 + Var 𝑒𝑒3 = 1
【連立方程式】
𝑎𝑎11 𝑎𝑎11 + Var(𝑒𝑒1) = 𝑎𝑎21 𝑎𝑎21 + Var(𝑒𝑒2) = 𝑎𝑎31 𝑎𝑎31 + Var(𝑒𝑒3) = 1
𝑎𝑎21 𝑎𝑎11 = 0.72 𝑎𝑎31 𝑎𝑎11 = 0.63 𝑎𝑎21 𝑎𝑎31 = 0.56
- 21.
- 22.
- 23.
- 24.
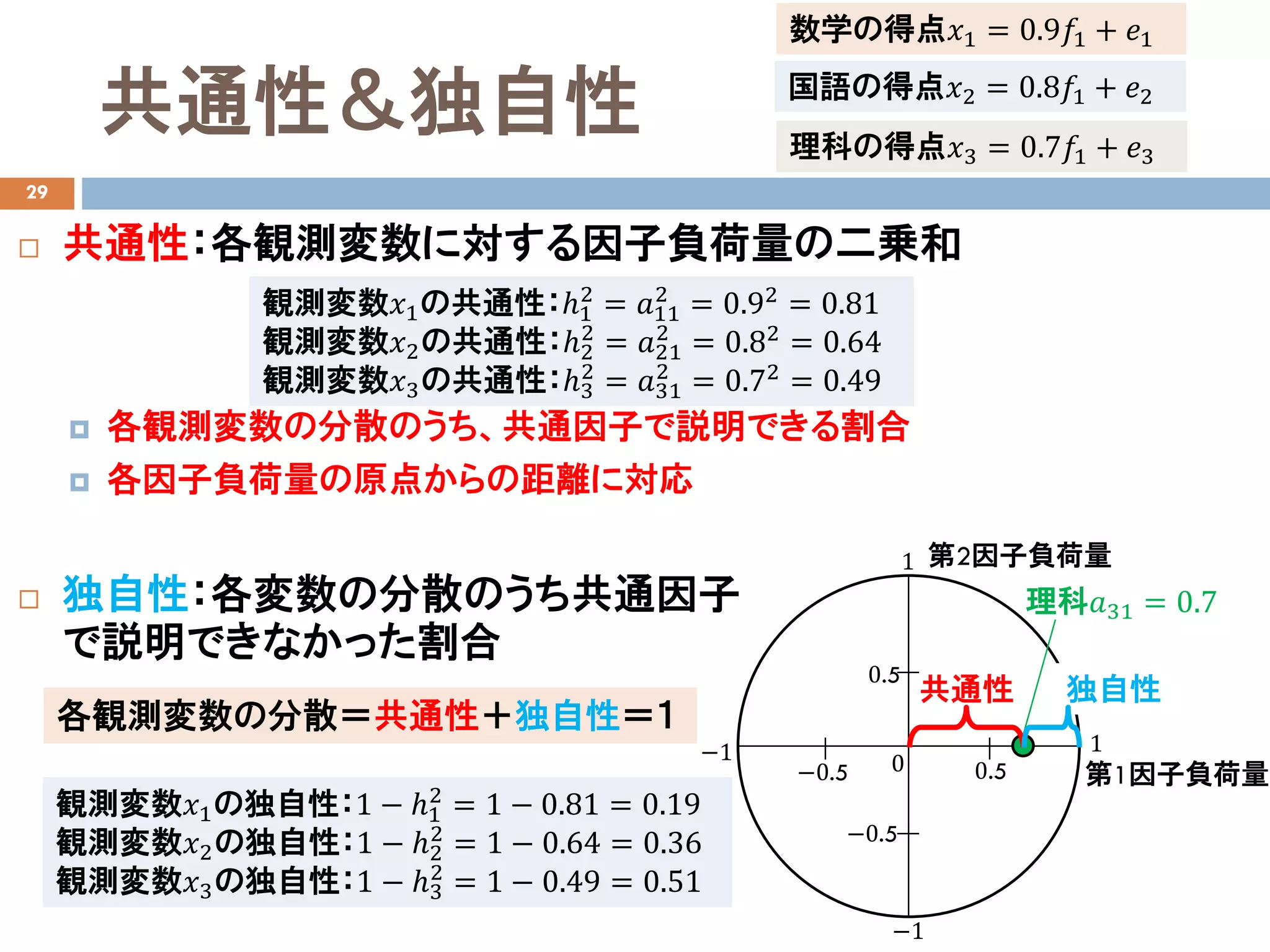
共通性&独自性
29
共通性:各観測変数に対する因子負荷量の二乗和
各観測変数の分散のうち、共通因子で説明できる割合
各因子負荷量の原点からの距離に対応
独自性:各変数の分散のうち共通因子
で説明できなかった割合
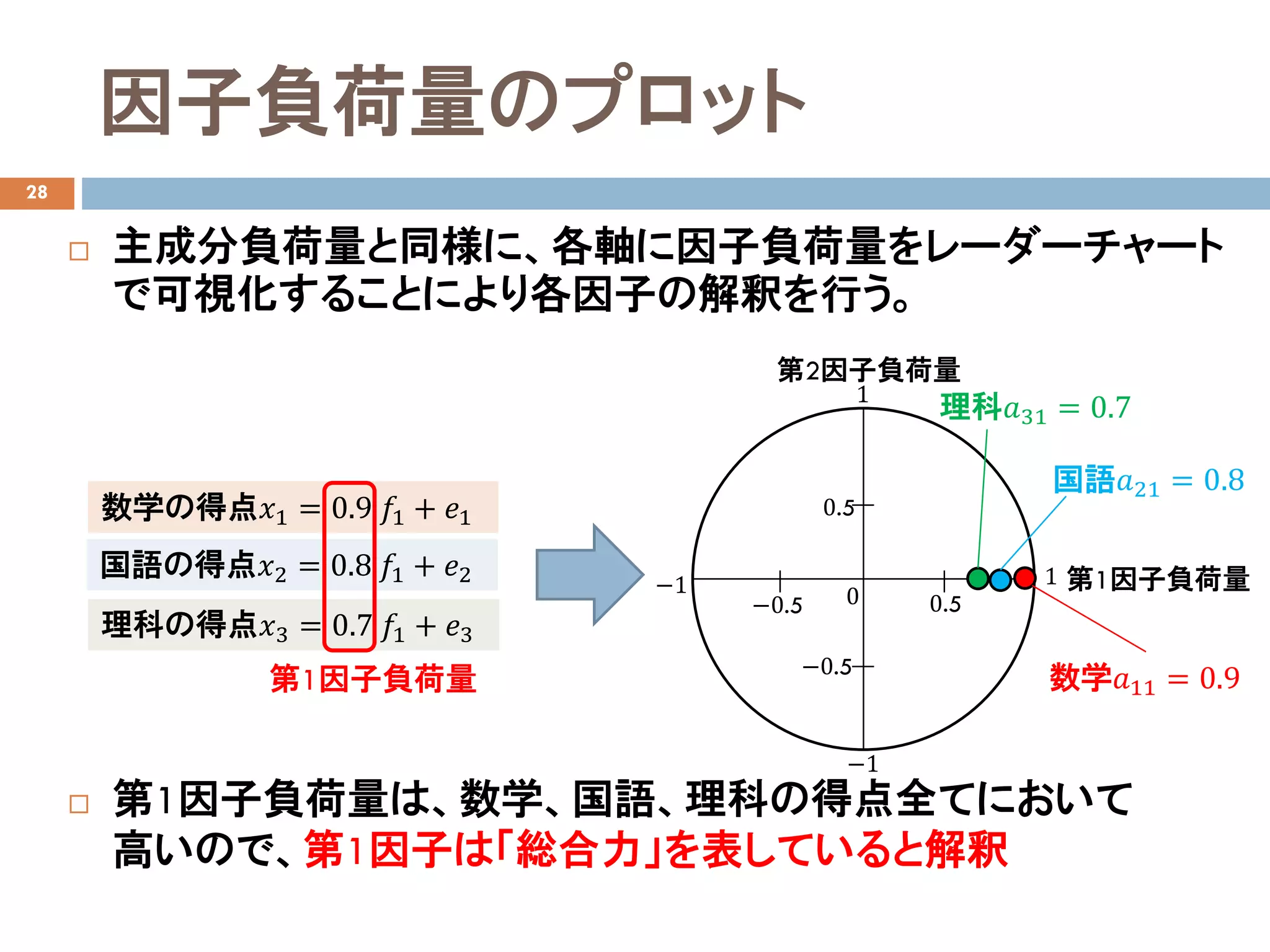
数学の得点𝑥𝑥1 = 0.9𝑓𝑓1 + 𝑒𝑒1
国語の得点𝑥𝑥2 = 0.8𝑓𝑓1 + 𝑒𝑒2
理科の得点𝑥𝑥3 = 0.7𝑓𝑓1 + 𝑒𝑒3
観測変数𝑥𝑥1の共通性:ℎ1
2
= 𝑎𝑎11
2
= 0.92
= 0.81
観測変数𝑥𝑥2の共通性:ℎ2
2
= 𝑎𝑎21
2
= 0.82
= 0.64
観測変数𝑥𝑥3の共通性:ℎ3
2
= 𝑎𝑎31
2
= 0.72
= 0.49
第1因子負荷量
第2因子負荷量
0−1 1
−0.5 0.5
1
−0.5
0.5
−1
理科𝑎𝑎31 = 0.7
共通性 独自性
各観測変数の分散=共通性+独自性=1
観測変数𝑥𝑥1の独自性:1 − ℎ1
2
= 1 − 0.81 = 0.19
観測変数𝑥𝑥2の独自性:1 − ℎ2
2
= 1 − 0.64 = 0.36
観測変数𝑥𝑥3の独自性:1 − ℎ3
2
= 1 − 0.49 = 0.51
- 25.
- 26.
- 27.