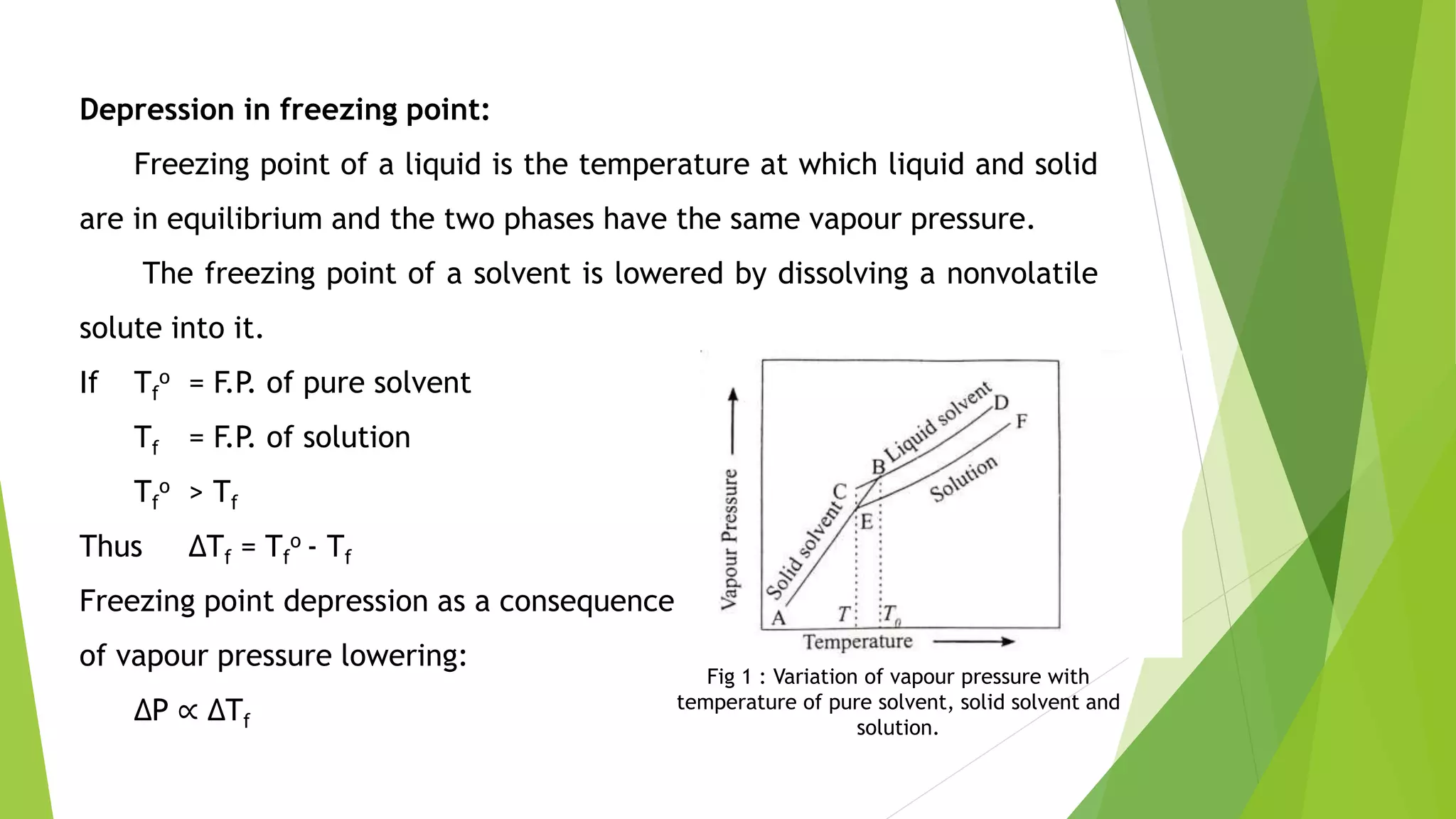
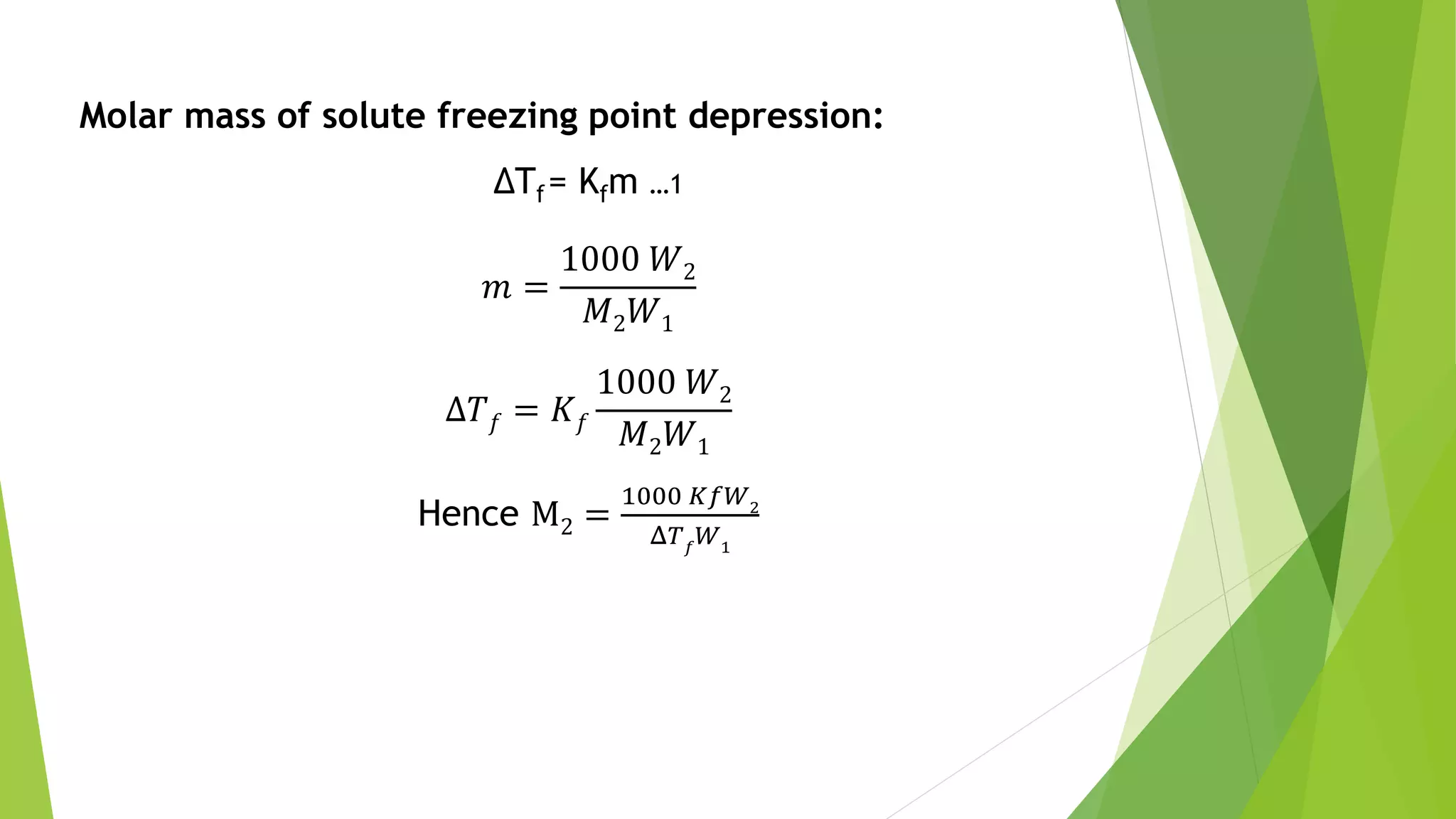
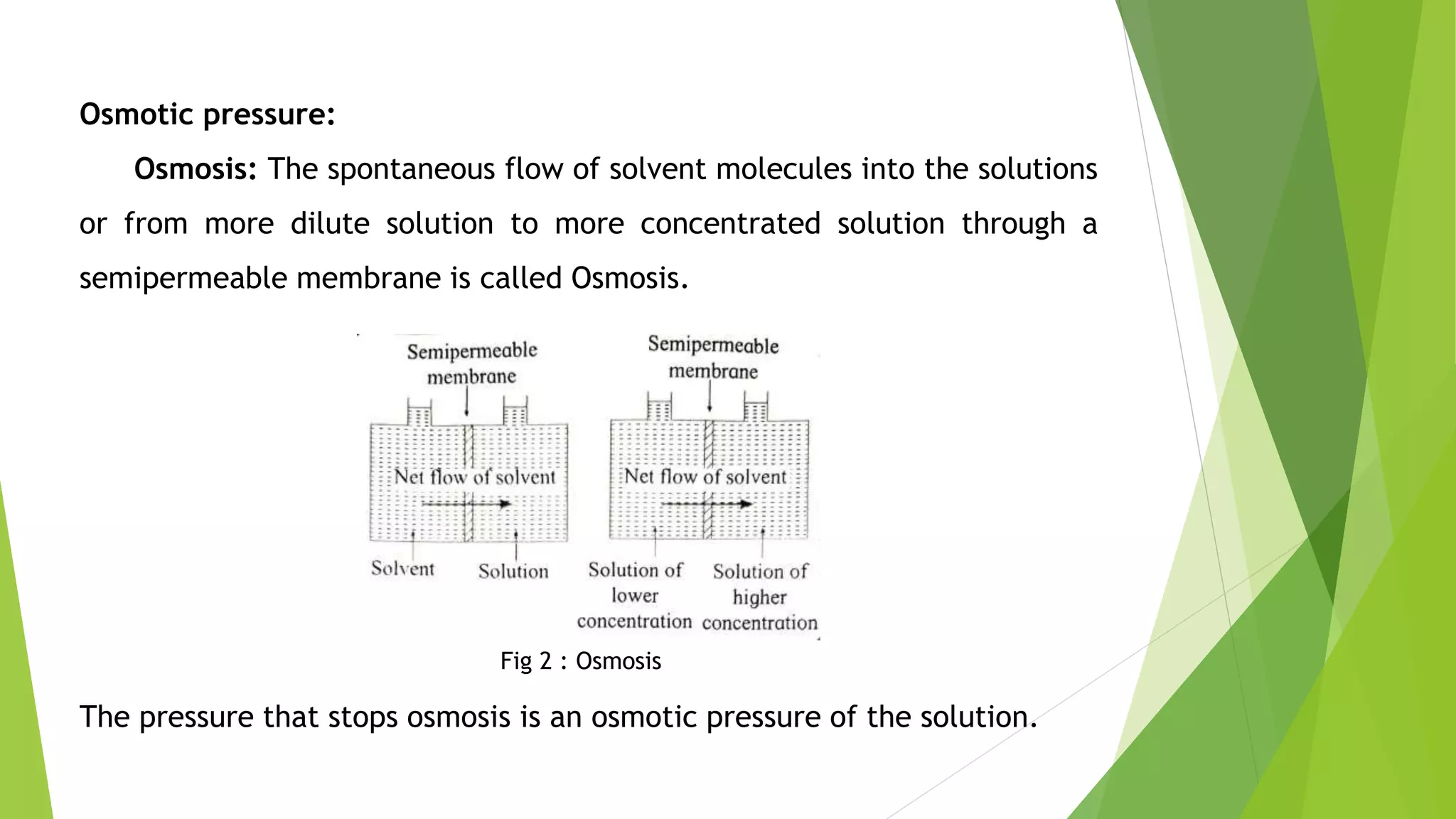
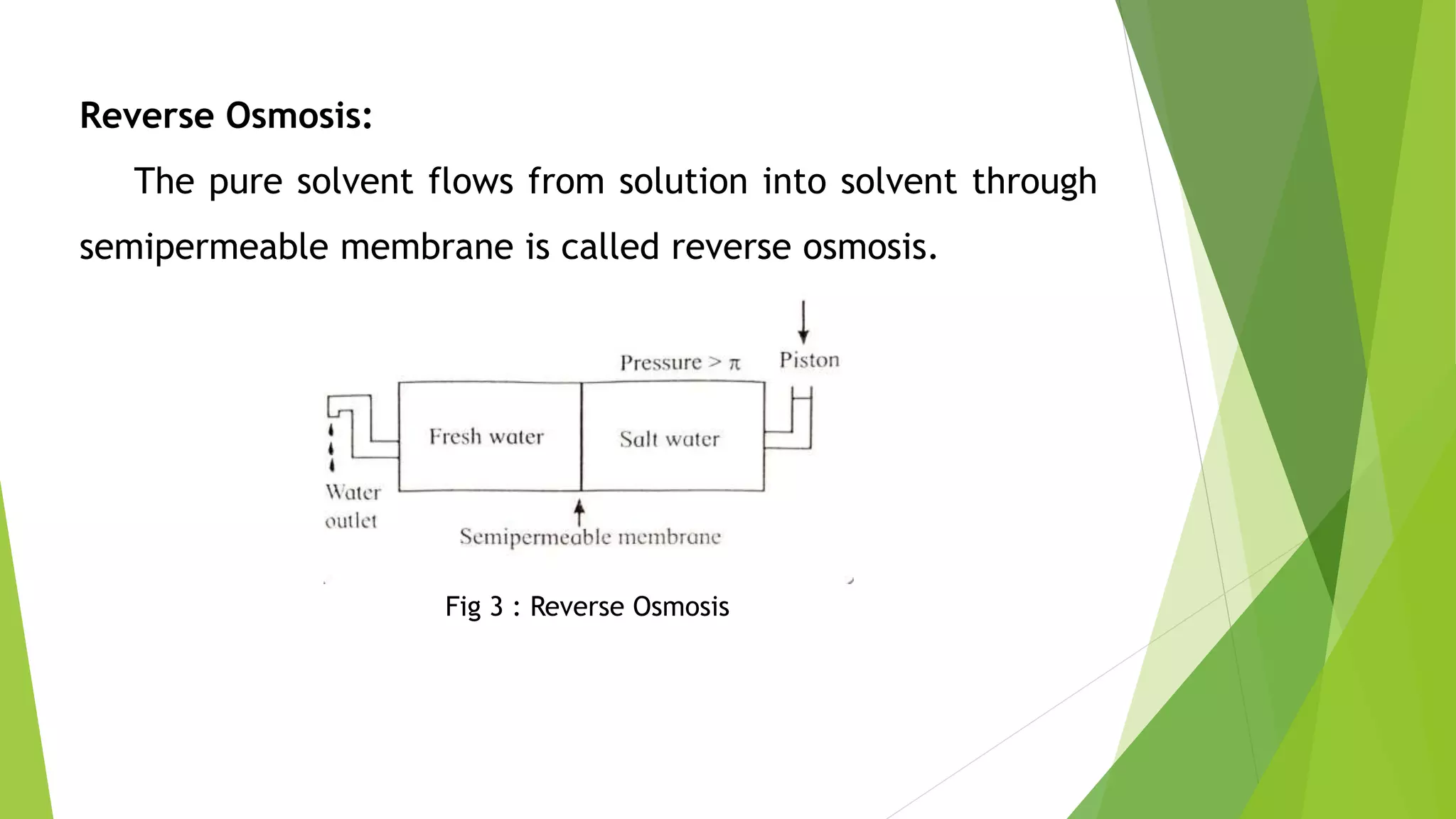
This document discusses colligative properties of solutions such as freezing point depression, boiling point elevation, and osmotic pressure. It explains that these properties are affected by the number of particles in solution. For electrolyte solutions, the properties are greater than nonelectrolyte solutions of the same concentration due to dissociation of ions. The document also defines terms like isotonic, hypertonic, and hypotonic solutions and introduces the Van't Hoff factor to relate colligative properties of electrolytes to their degree of dissociation.

1. The Malegaon High School & Jr. College
Malegaon, (Nashik), 423203
3rd Lecture on Solutions
Chemistry Part I, 12th Science
By
Rizwana Mohammad

2. Depression in freezing point:
Freezing point of a liquid is the temperature at which liquid and solid
are in equilibrium and the two phases have the same vapour pressure.
The freezing point of a solvent is lowered by dissolving a nonvolatile
solute into it.
If Tf
o = F.P. of pure solvent
Tf = F.P. of solution
Tf
o > Tf
Thus ΔTf = Tf
o - Tf
Freezing point depression as a consequence
of vapour pressure lowering:
ΔP ∝ ΔTf
Fig 1 : Variation of vapour pressure with
temperature of pure solvent, solid solvent and
solution.

3. Freezing point depression and concentration of solute:
ΔTf ∝ m
ΔTf = Kf m
If m=1, ΔTf = Kf
Kf = F.P. depression constant or cryoscopic constant
The cryoscopic constant is the depression in freezing point
produced by 1 molal solution of non volatile solute
Unit of Kf =
Δ𝑇 𝑓
𝑚
=
𝐾
𝑀𝑜𝑙 𝑘𝑔
−
1 = K kg mol-1

4. Molar mass of solute freezing point depression:
ΔTf= Kfm …1
𝑚 =
1000 𝑊2
𝑀2 𝑊1
Δ𝑇 𝑓 = 𝐾 𝑓
1000 𝑊2
𝑀2 𝑊1
Hence M2 =
1000 𝐾𝑓𝑊2
Δ𝑇 𝑓
𝑊1

5. Osmotic pressure:
Osmosis: The spontaneous flow of solvent molecules into the solutions
or from more dilute solution to more concentrated solution through a
semipermeable membrane is called Osmosis.
Fig 2 : Osmosis
The pressure that stops osmosis is an osmotic pressure of the solution.

6. • Isotonic solution: Two or more solutions having the same
osmotic pressure are said to be isotonic solution.
• Hypertonic solution: If two solutions have unequal osmotic
pressures, the solutions with higher osmotic pressure is
called hypertonic solution.
• Hypotonic solution: If two solutions have unequal osmotic
pressures, the solution with lower osmotic pressure is said
to be hypotonic solution.

7. Osmotic pressure and concentration of solution:
For very dilute solution, osmotic pressure follows the
equation, 𝜋 =
𝑛2
𝑅𝑇
𝑉
…1
V = Volume of solution in dm3
n2 = Moles of nonvolatile solute
R = Gas constant, 0.08206 dm3 atm k-1 mol-1
𝜋 = Osmotic pressure in atm.
𝑛2
𝑉
= Molarity
Therefore
𝜋 = MRT …2

8. Molar mass of solute from osmotic pressure:
Consider, 𝜋 =
𝑛2
𝑅𝑇
𝑉
n2 =
𝑊2
𝑀2
𝜋 =
𝑊2
𝑅𝑇
𝑀2
𝑉
M2 =
𝑊2
𝑅𝑇
𝜋𝑉

9. Reverse Osmosis:
The pure solvent flows from solution into solvent through
semipermeable membrane is called reverse osmosis.
Fig 3 : Reverse Osmosis

10. Colligative properties of electrolytes:
Following are experimental observations for the colligative behavior
of electrolytes:
i. The solutions of electrolytes also exhibit colligative properties which
do not obey the relations of non electrolytes.
ii. The colligative properties of the solutions of electrolytes are greater
than those for solutions of nonelectrolytes.
iii. The molar masses of electrolytes are lower than the formula masses.
Electrolytes dissociate into two or more ions when dissolved in
water, the number of particles increases, therefore the colligative
properties of electrolytes solutions are higher than the nonelectrolyte
solutions.

11. Van’t Hoff factor (i):
i =
𝑐𝑙𝑙𝑖𝑔𝑎𝑡𝑖𝑣𝑒 𝑝𝑟𝑜𝑝𝑒𝑟𝑡𝑦 𝑜𝑓 𝑒𝑙𝑒𝑐𝑡𝑟𝑜𝑙𝑦𝑡𝑒 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛
𝑐𝑜𝑙𝑙𝑖𝑔𝑎𝑡𝑖𝑣𝑒 𝑝𝑟𝑜𝑝𝑒𝑟𝑡𝑦 𝑜𝑓 𝑛𝑜𝑛𝑒𝑙𝑒𝑐𝑡𝑟𝑜𝑙𝑦𝑡𝑒 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛 𝑜𝑓 𝑡ℎ𝑒 𝑠𝑎𝑚𝑒 𝑐𝑜𝑛𝑐𝑒𝑛𝑡𝑟𝑎𝑡𝑖𝑜𝑛
=
(Δ𝑇 𝑓)
Δ𝑇 𝑓 𝑜
=
(Δ𝑇 𝑏)
Δ𝑇 𝑏 𝑜
=
(Δ𝑃)
Δ𝑃 𝑜
=
(𝜋)
𝜋 𝑜
Van’t Hoff factor is also defined as
𝑖 =
𝑎𝑐𝑡𝑢𝑎𝑙 𝑚𝑜𝑙𝑒𝑠 𝑜𝑓 𝑝𝑎𝑟𝑡𝑖𝑐𝑙𝑒𝑠 𝑖𝑛 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛 𝑎𝑓𝑡𝑒𝑟 𝑑𝑖𝑠𝑠𝑜𝑐𝑖𝑎𝑡𝑖𝑜𝑛
𝑚𝑜𝑙𝑒𝑠 𝑜𝑓 𝑓𝑜𝑟𝑚𝑢𝑙𝑎 𝑢𝑛𝑖𝑡𝑠 𝑑𝑖𝑠𝑠𝑜𝑙𝑣𝑒𝑑 𝑖𝑛 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛
=
𝑓𝑜𝑟𝑚𝑢𝑙𝑎 𝑚𝑎𝑠𝑠 𝑜𝑓 𝑠𝑢𝑏𝑠𝑡𝑎𝑛𝑐𝑒
𝑜𝑏𝑠𝑒𝑟𝑣𝑒𝑑 𝑚𝑜𝑙𝑎𝑟 𝑚𝑎𝑠𝑠 𝑜𝑓 𝑠𝑢𝑏𝑠𝑡𝑎𝑛𝑐𝑒
𝑖 =
𝑀𝑡ℎ𝑒𝑜𝑟𝑒𝑡𝑖𝑐𝑎𝑙
𝑀 𝑜𝑏𝑠𝑒𝑟𝑣𝑒𝑑

12. Modification of expressions of colligative properties:
The modified equations are
i. Δ𝑃 = 𝑖 𝑃1
0 𝑥2 = 𝑖
𝑊2
𝑀1
𝑀2
𝑊1
ii. Δ𝑇 𝑏 = 𝑖 𝐾𝑏 𝑚 = 𝑖
1000 𝐾𝑏𝑊2
𝑀2
𝑊1
iii. Δ𝑇 𝑓 = 𝑖
1000 𝐾𝑓𝑊2
𝑀2
𝑊1
iv. 𝜋 = 𝑖𝑀𝑅𝑇 = 𝑖
𝑊2
𝑅𝑇
𝑀2
𝑉

13. Relation between Van’t Hoff factor and degree of dissociation:
Consider an electrolyte AxBy that dissociates in aqueous solution as
𝐴𝑥𝐵𝑦 ⇌ 𝑥𝐴 𝑦
+ 𝑦𝐵 𝑥
Initially 1 mol 0 0
At eqm (1-α) mol (xα) (yα)
Total moles after dissociation
=(1-α) + (xα) + (yα)
=1+α (x+y-1)
=1+α (n-1)
where n = x+y = moles of ions obtained from dissociation of 1 mole of
electrolyte

14. 𝑖 =
𝑎𝑐𝑡𝑢𝑎𝑙 𝑚𝑜𝑙𝑒𝑠 𝑜𝑓 𝑝𝑎𝑟𝑡𝑖𝑐𝑙𝑒𝑠 𝑜𝑛 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛 𝑎𝑓𝑡𝑒𝑟 𝑑𝑖𝑠𝑠𝑜𝑐𝑖𝑎𝑡𝑖𝑜𝑛
𝑚𝑜𝑙𝑒𝑠 𝑜𝑓 𝑓𝑜𝑟𝑚𝑢𝑙𝑎 𝑢𝑛𝑖𝑡𝑠 𝑑𝑖𝑠𝑠𝑜𝑙𝑣𝑒𝑑 𝑖𝑛 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛
=
1+ α (𝑛 −1)
1
𝑖 = 1 + α (𝑛 − 1)
α =
𝑖 − 1
𝑛 − 1