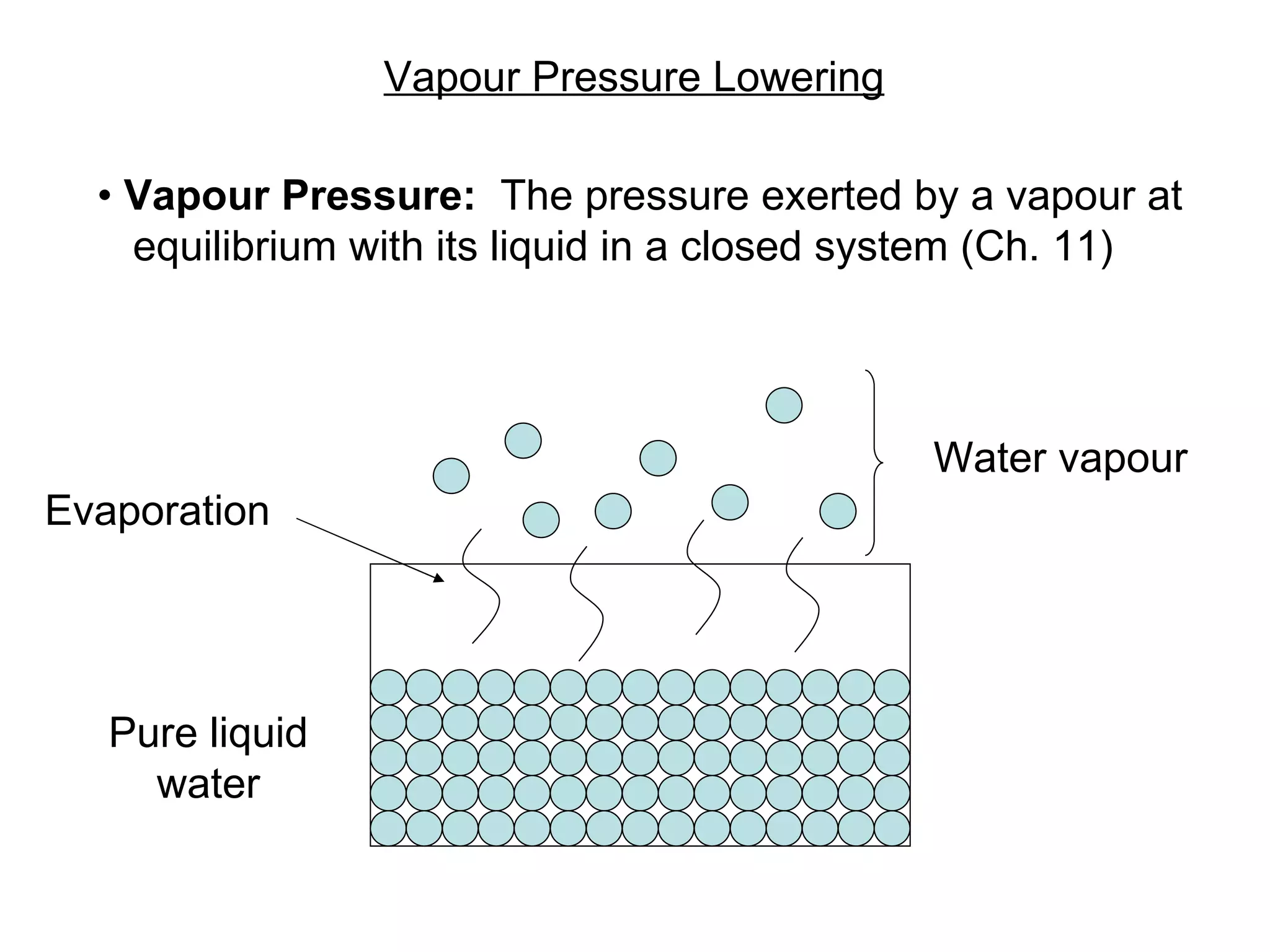
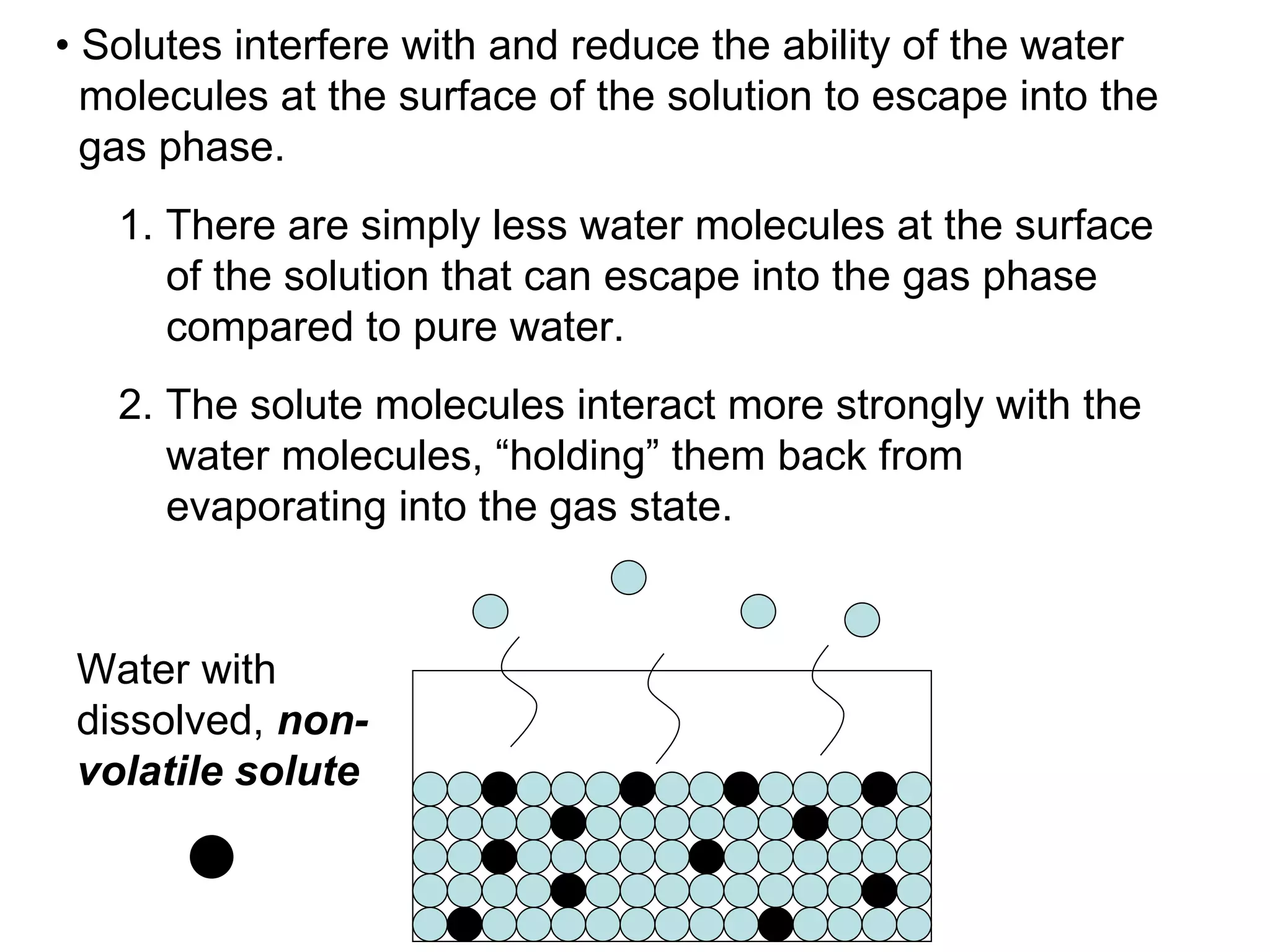
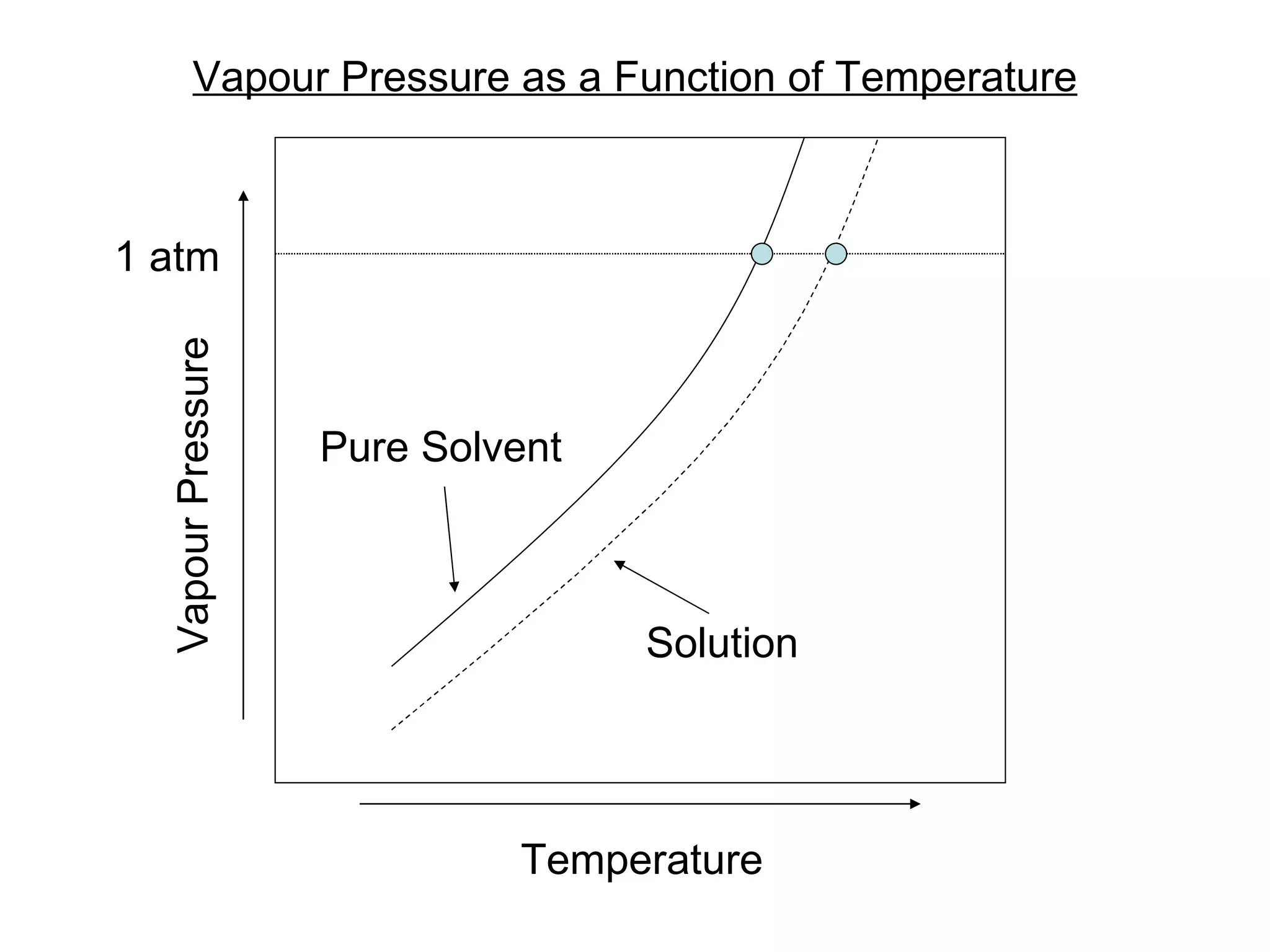
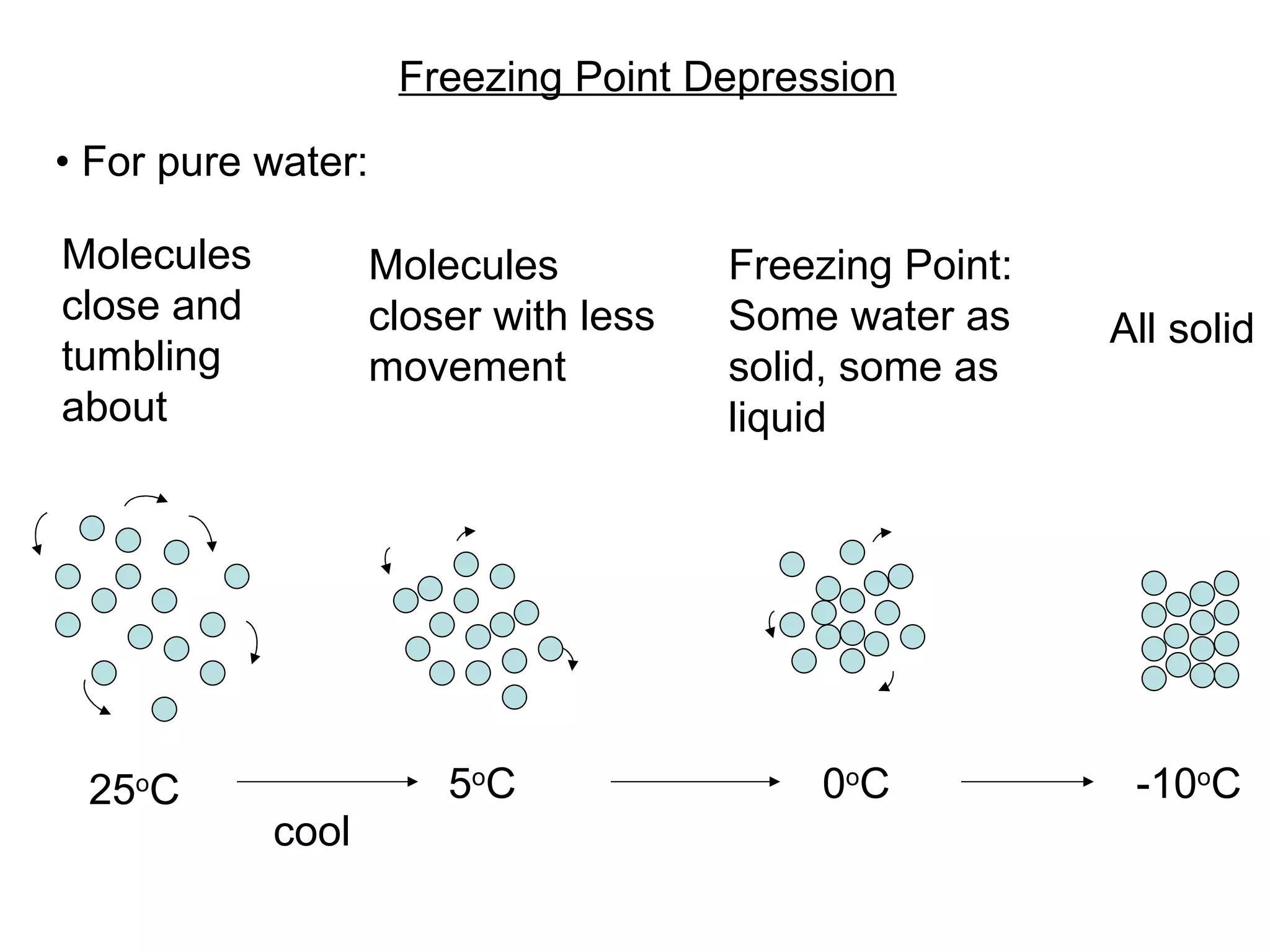
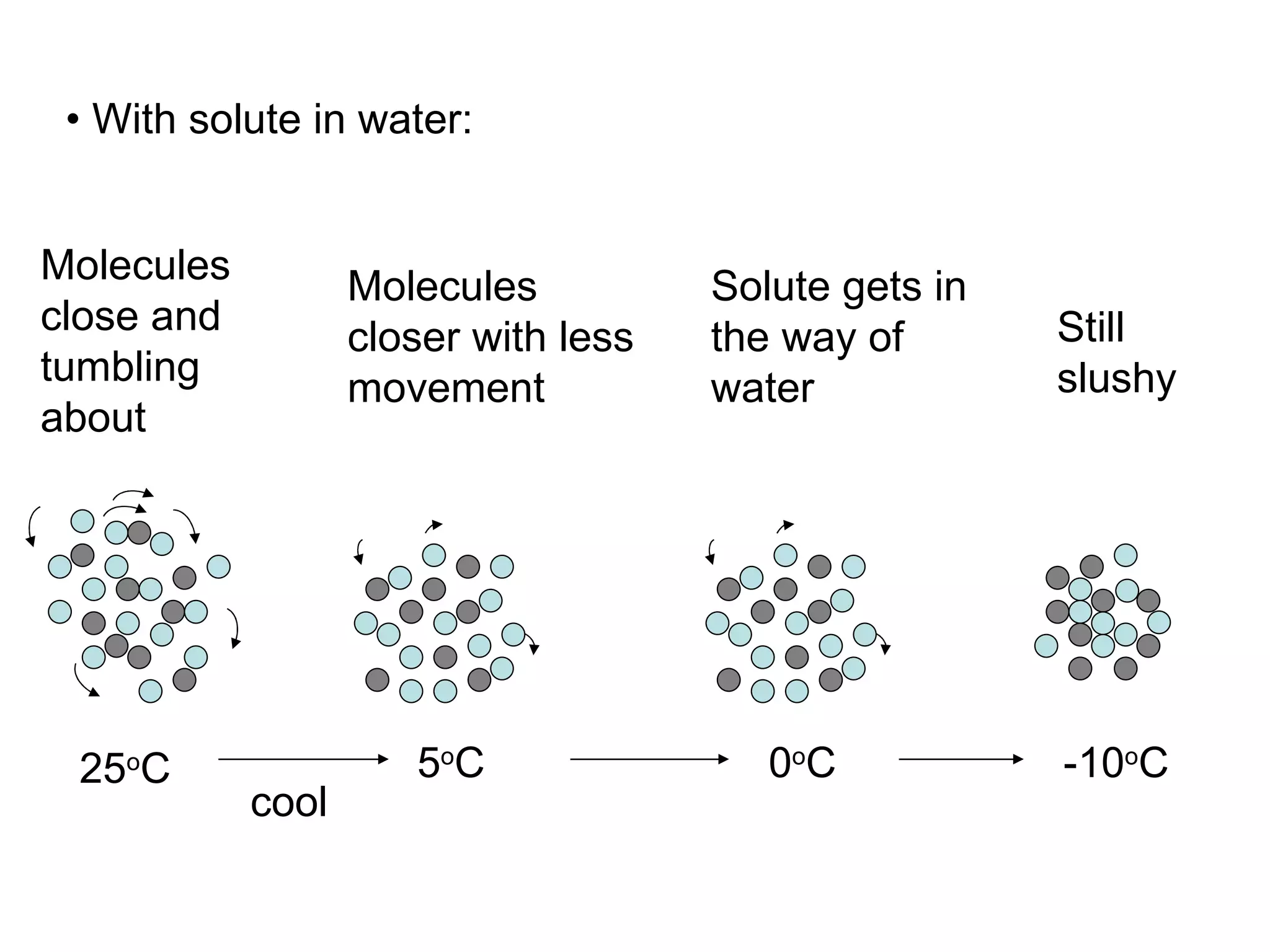
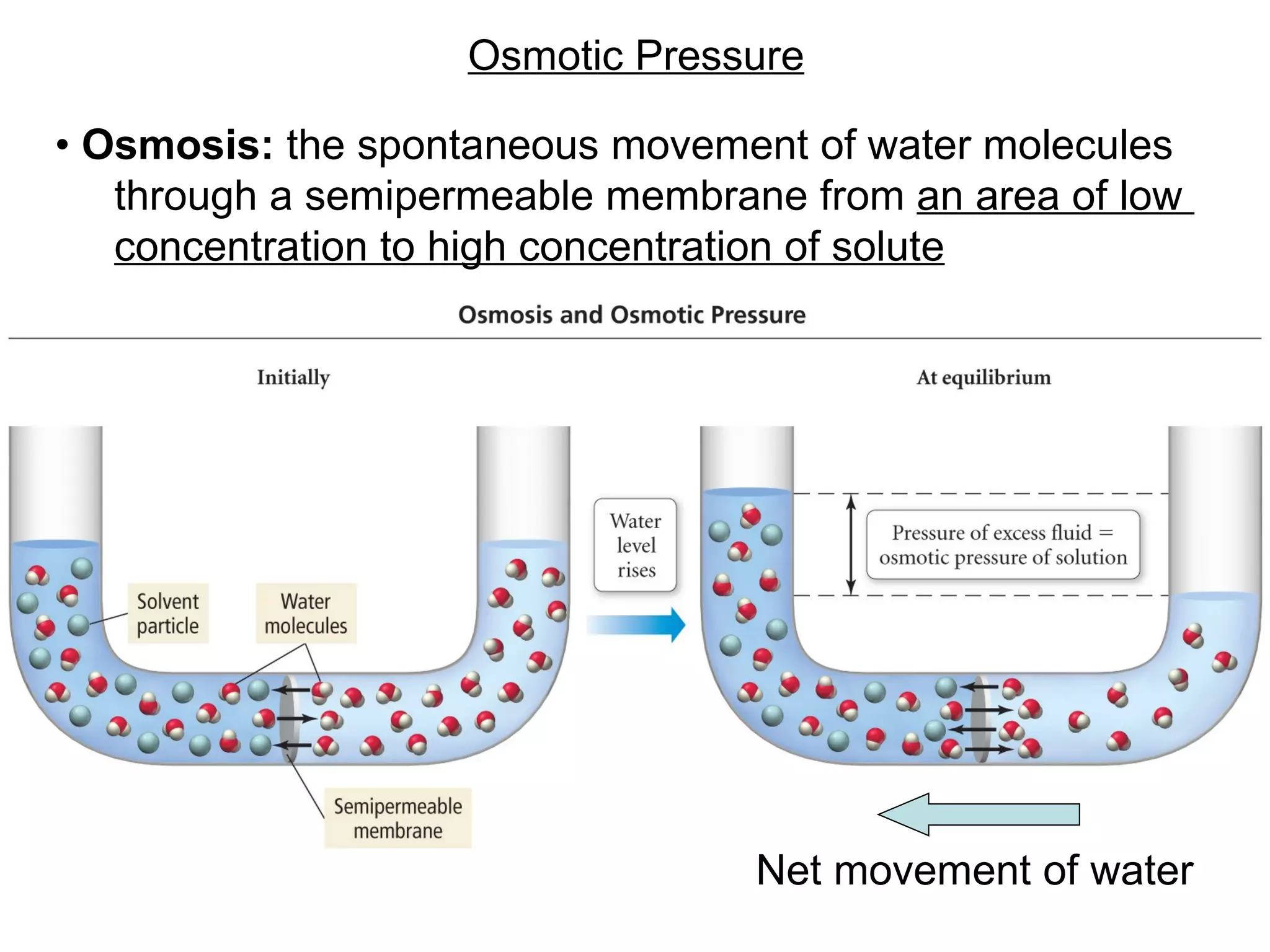
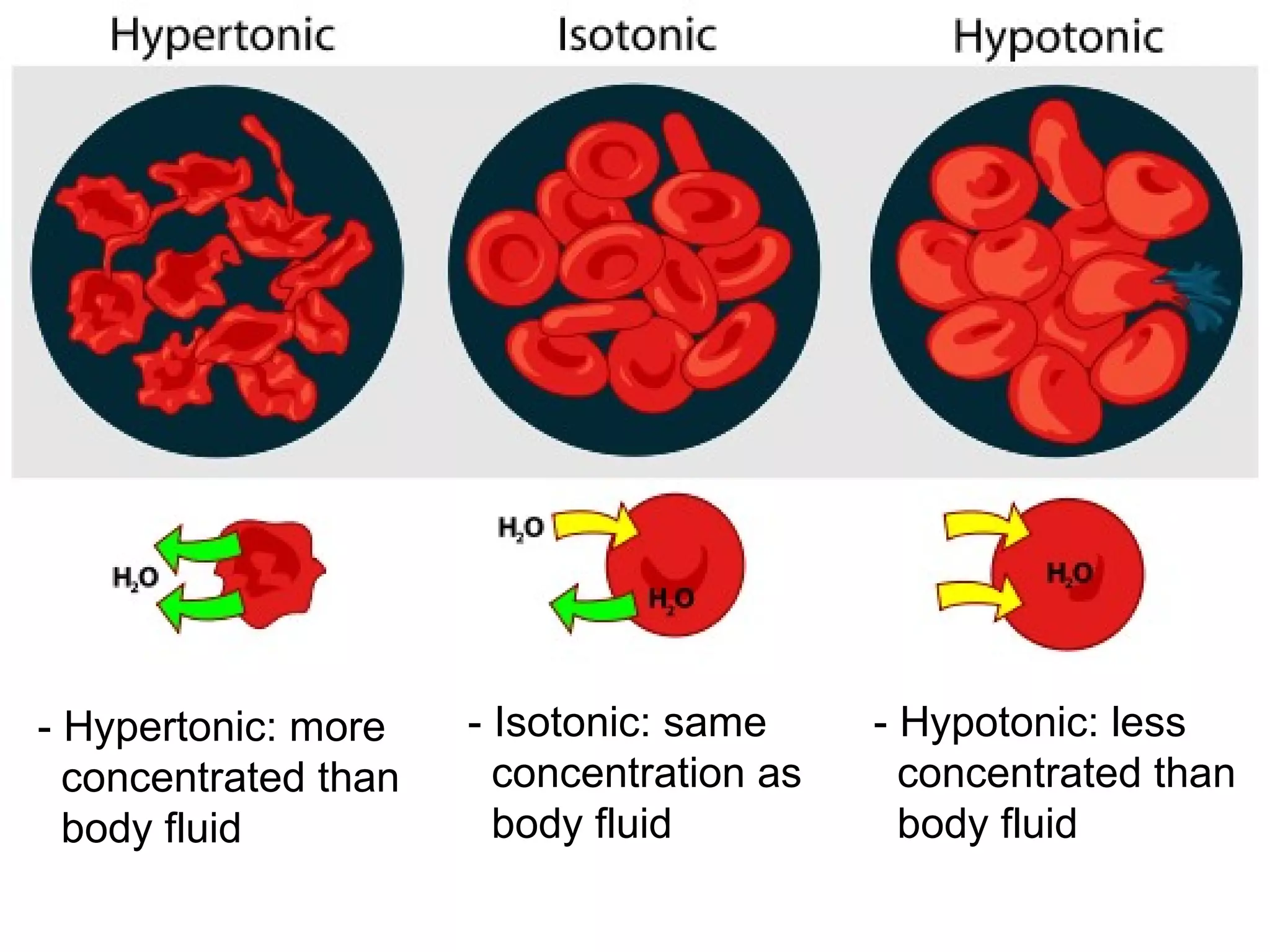
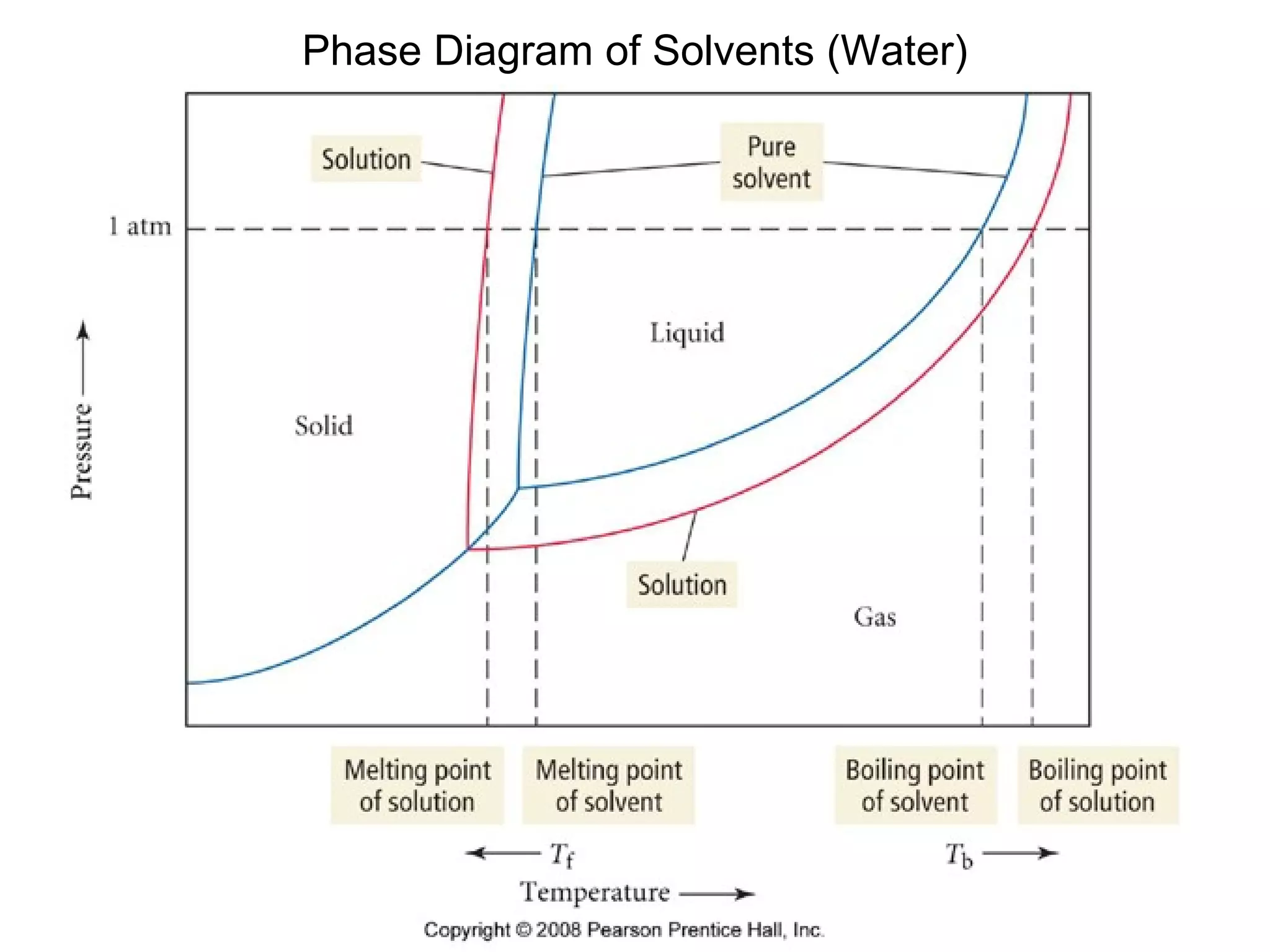
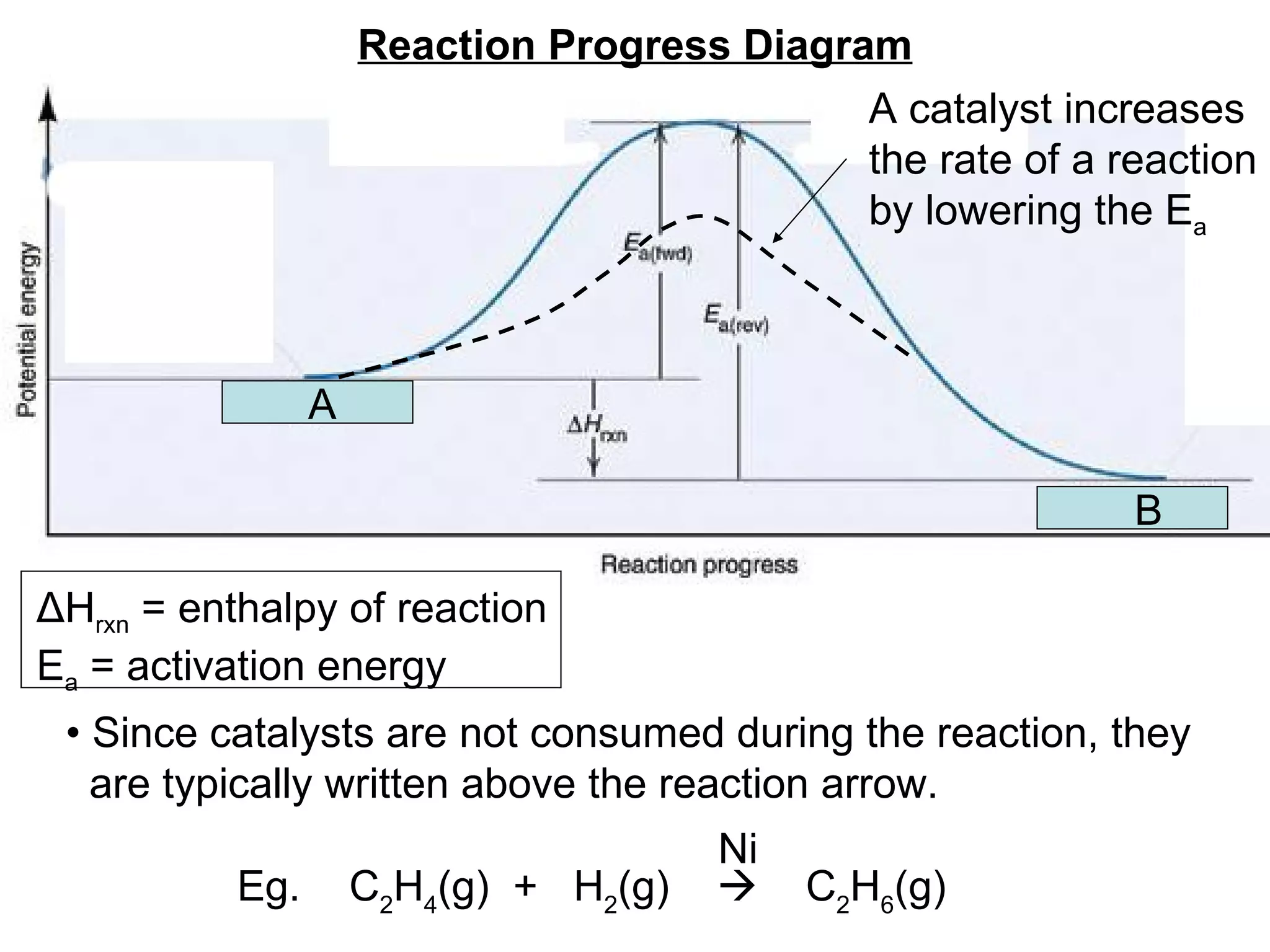
The document discusses colligative properties of solutions, which depend only on the number of solute particles and not their type. It describes how adding solute particles lowers vapor pressure and freezing point and raises boiling point of the solvent. Specifically, it provides equations to calculate boiling point elevation, freezing point depression, and osmotic pressure based on molality and van't Hoff factor of the solution.

1. • The number of solute particles, not the type, changes the properties of a solution, called colligative properties. 3. Freezing point depression 1. Vapour pressure lowering 2. Boiling point elevation 4. Changes in osmotic pressure Colligative Properties (Ch. 12.7) Inverse Relationship

2. • Vapour Pressure: The pressure exerted by a vapour at equilibrium with its liquid in a closed system (Ch. 11) Pure liquid water Water vapour Evaporation Vapour Pressure Lowering

3. Water with dissolved, non- volatile solute • Solutes interfere with and reduce the ability of the water molecules at the surface of the solution to escape into the gas phase. 1. There are simply less water molecules at the surface of the solution that can escape into the gas phase compared to pure water. 2. The solute molecules interact more strongly with the water molecules, “holding” them back from evaporating into the gas state.

4. Vapour Pressure as a Function of Temperature Temperature Vapour Pressure 1 atm Pure Solvent Solution

5. • Boiling point is defined at the point where the vapour pressure of a substance equals the external pressure , usually that of the atmosphere. - Since solutes lower vapour pressure, a higher temperature is required for a solution to equal the external pressure Boiling Point Elevation ΔT b = K b . m . i • To calculate boiling temperature elevation ΔT b : - where K b is the boiling point elevation constant (for water it is 0.512 o C/ m ) and m is the molality of the solution.

6. - i is the vant Hoff factor . It represents the stoichiometry of particles produced when a compound dissolves in solution under ideal conditions Eg. Sucrose has an i factor of 1 NaCl has an i factor of 2 MgCl 2 has an i factor of 3 Tb solution = Tb solvent + ΔT b Boiling point change (elevation) Boiling point of solution Boiling point of solvent (usually water 100 o C) • The boiling point of a solution will be higher than that of the pure solvent:

7. Freezing Point Depression Molecules close and tumbling about Molecules closer with less movement Freezing Point: Some water as solid, some as liquid All solid • For pure water: 25 o C cool 5 o C 0 o C -10 o C

8. 25 o C Molecules close and tumbling about Molecules closer with less movement Solute gets in the way of water • With solute in water: cool 5 o C 0 o C -10 o C Still slushy

9. ΔT f = K f . m . i • To calculate freezing temperature depression: - where K f is the freezing poing depression constant (for water it is 1.86 o C/ m ) and m is the molality of the solution. Tf solution = Tf solvent – ΔT f Freezing point change (depression) Freezing point of solvent (usually water 0 o C) Freezing point of solution • The freezing point of a solution will be lower than that of the pure solvent:

10. Osmotic Pressure • Osmosis: the spontaneous movement of water molecules through a semipermeable membrane from an area of low concentration to high concentration of solute Net movement of water

11. - Isotonic: same concentration as body fluid - Hypertonic: more concentrated than body fluid - Hypotonic: less concentrated than body fluid

12. π = MRT i • To calculate osmotic pressure: - Where π is osmotic pressure, M is concentration (molarity), R is the universal gas constant (8.314 kPa . L . mol -1 . K -1 ), T is the temperature in Kelvin, and i is the vant Hoff factor. Technically, colligative property calculations apply only in solutions that are “ideal”. This means that the solution cannot be overly concentrated in solute.

13. Phase Diagram of Solvents (Water)

14. Molar Mass Determination From Colligative Properties 1. 2.00 g of a salt is dissolved in 15.00 ml of water (assume density is 1.00 g/ml). This salt solution freezes at -3.6 o C. What is the identity of the salt? (K f = 1.86 o C/ m ) a) BaCl 2 or b) MgCl 2 208 g/mol 95.3 g/mol 2. 1.158 grams of a non-dissociating protein is dissolved in 50.00 ml of water. This protein solution generates an osmotic pressure of 2.09 kPa at 25 o C. What is the molar mass of the protein? R = 8.314 kPa . L/mol . K o K = o C + 273.15

15. Kinetics (Ch. 13) • Kinetics is the study of the change in concentrations of the reactants or products over time , or in other words, the rate of the reaction .

16. Time (s) Speed (km/h) 200 150 100 50 250 Car Acceleration Profiles Car A Car B

17. Collision Theory/Model • The particles involved in a reaction must physically collide with each other with enough energy AND in the proper orientation for a reaction to occur

18. • Reactions require that the particles/molecules collide in the correct orientation.

19. • Factors That Affect the Rate of a Reaction: 1. The concentration of reactants: If we have more particles of A and B, it will increase the chance of them colliding together, so the greater the rate of the reaction 2. The physical state (surface area): Certain physical states allow for greater mixing of the reactants, thus increasing rate of reaction 3. Temperature: Not all collisions result in a reaction. The energy of the collision must surpass the activation energy. 4. Catalysts: A substance that increases the rate of the chemical reaction but is not consumed by the reaction. Catalysts can be homogeneous or heterogeneous .

20. Reaction Progress Diagram • Since catalysts are not consumed during the reaction, they are typically written above the reaction arrow. A B A catalyst increases the rate of a reaction by lowering the E a Δ H rxn = enthalpy of reaction E a = activation energy C 2 H 4 (g) + H 2 (g)  C 2 H 6 (g) Ni Eg.

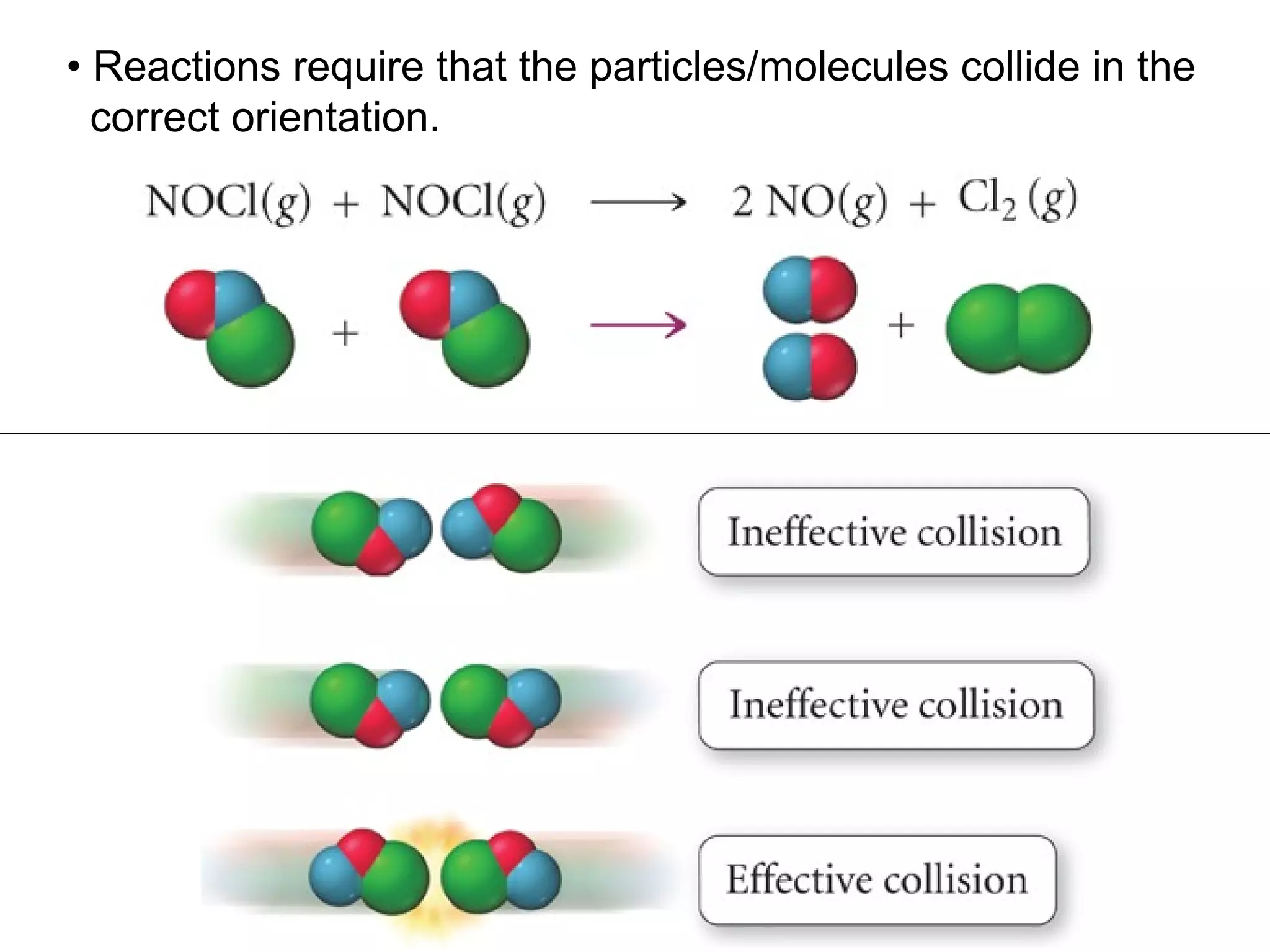
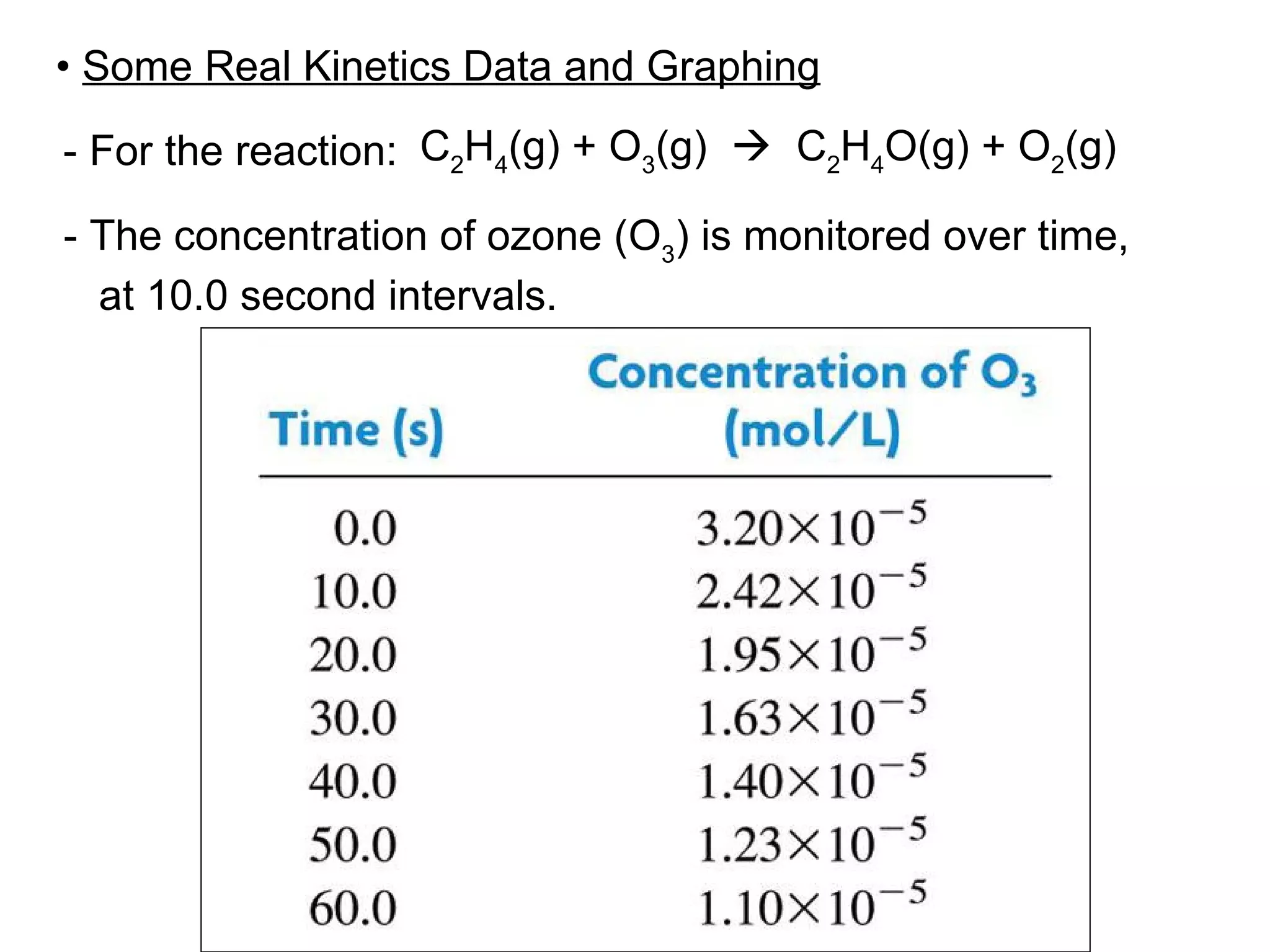
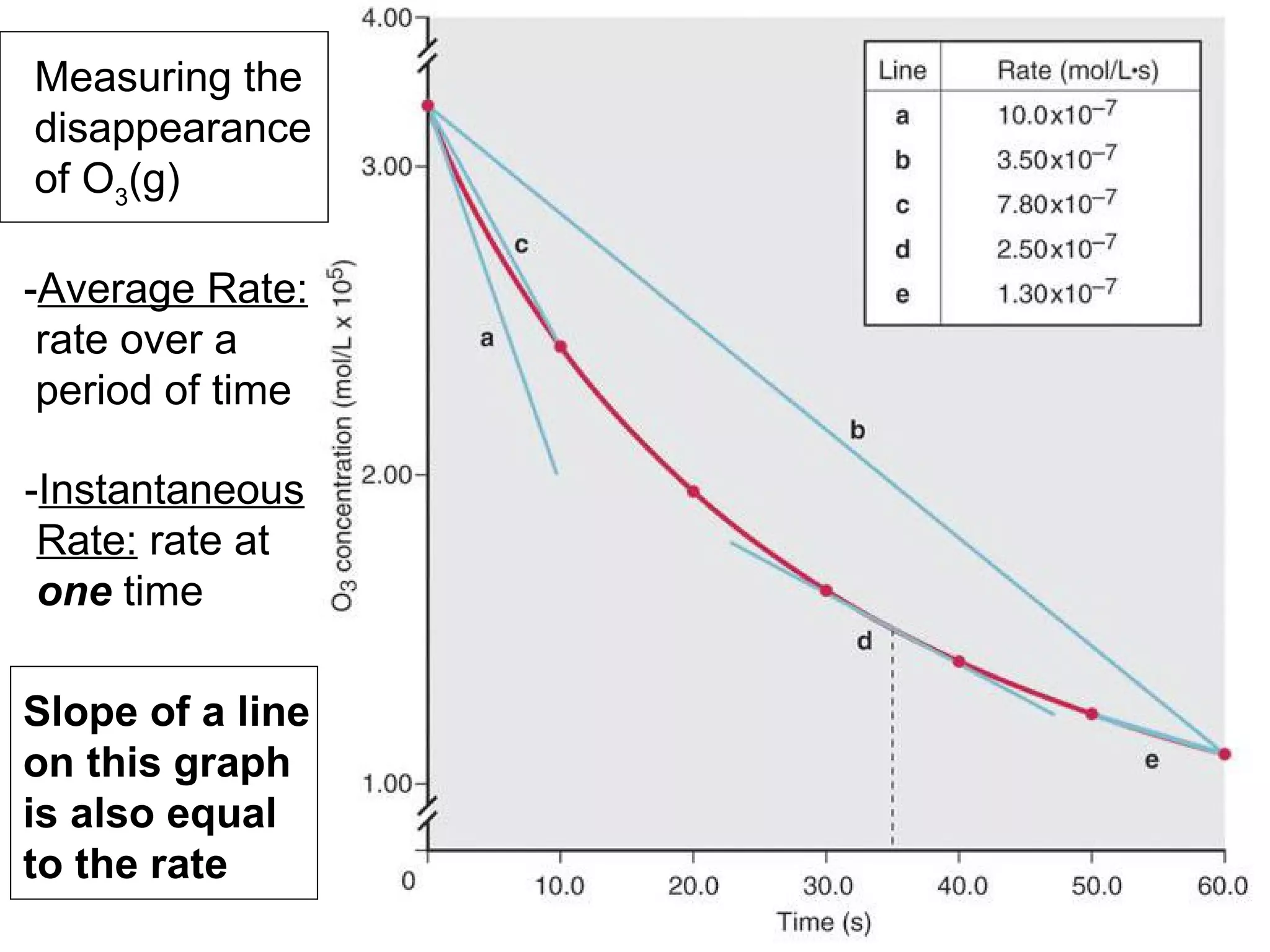
21. • Expressing Reaction Rate (of Reactants and Products) - Rate is defined as a change in some variable per unit of time. - If we measure the change in concentration of A over time, we can determine its reaction rate. Take the reaction A  B = = [ ], square brackets are short-hand notation for concentration Δ [A] Δ t [A] 2 - [A] 1 t 2 – t 1 There is a minus sign since A is disappearing in the reaction change in [A] change in time

22. - Alternatively, we could have also measured the rate of change in B. Since B is being produced, its change is positive Reaction A  B Finally, in this particular example. Since reactants disappear, the change is negative Since products are produced, the change is positive . Δ [A] Δ t Therefore rate = And is measured in units of M/time ( mol . L -1 . time -1 ) Δ [B] Δ t Δ [A] Δ t =

23. • For any general reaction of say a A + b B  c C + d D - Where the italicized letter is the stoichiometric coefficient - The rate expression of all reactants and products would be: Rate = Δ [B] Δ t Δ [A] Δ t = Δ [D] Δ t Δ [C] Δ t = 1 a 1 b = 1 c 1 d

24. C 2 H 4 (g) + O 3 (g)  C 2 H 4 O(g) + O 2 (g) - For the reaction: - The concentration of ozone ( O 3 ) is monitored over time, at 10.0 second intervals. • Some Real Kinetics Data and Graphing

25. Measuring the disappearance of O 3 (g) - Average Rate: rate over a period of time - Instantaneous Rate: rate at one time Slope of a line on this graph is also equal to the rate