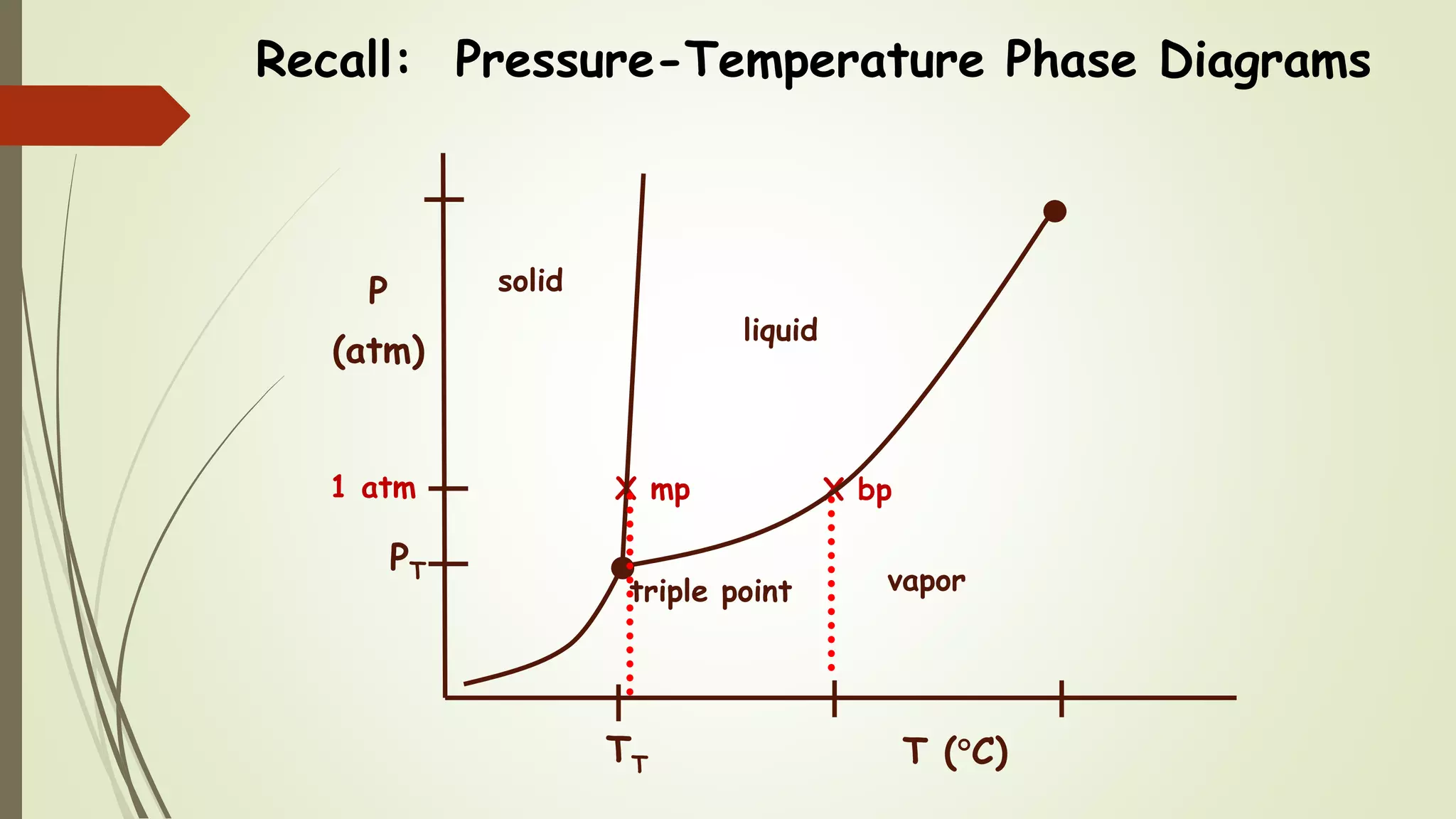
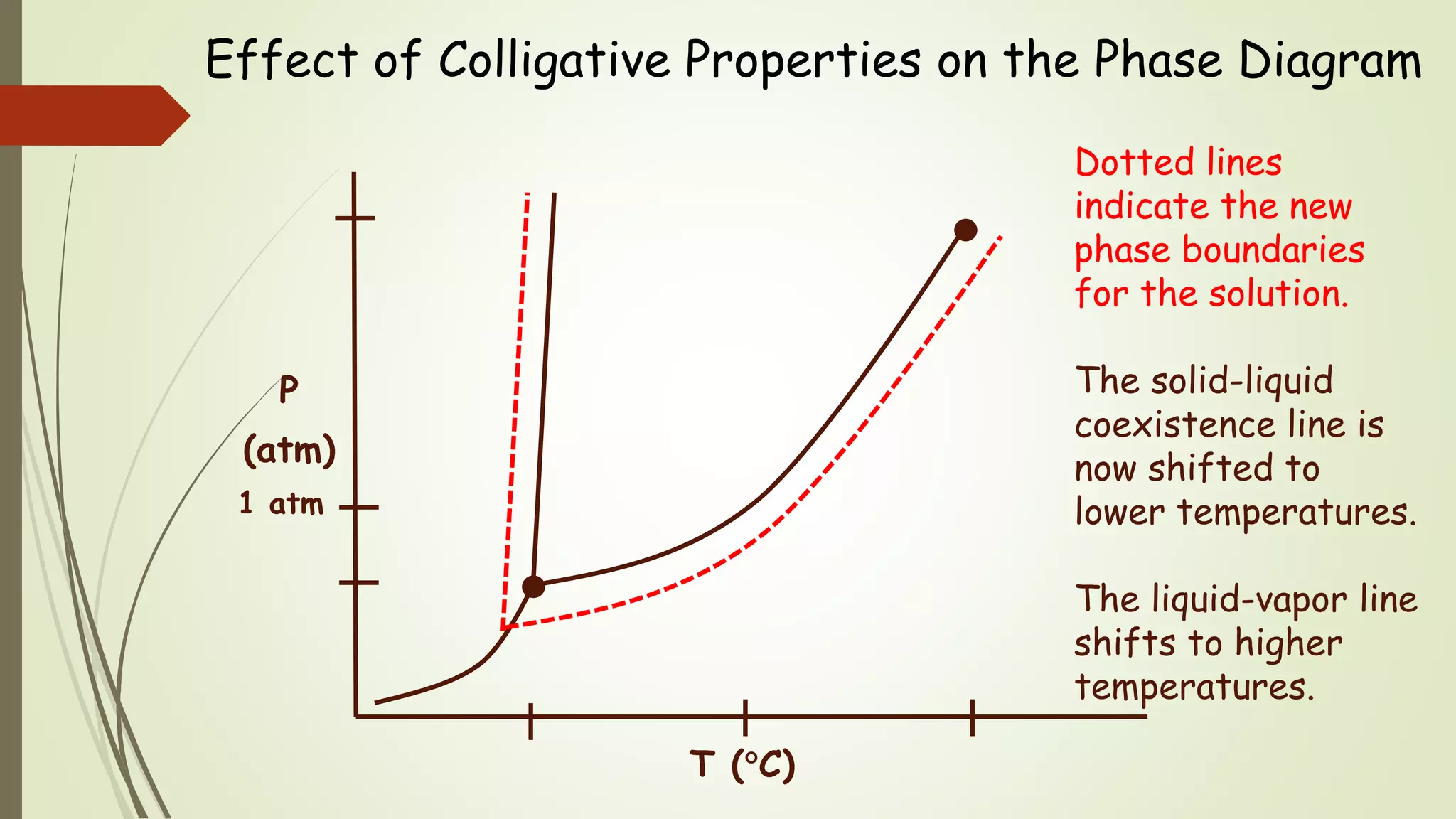
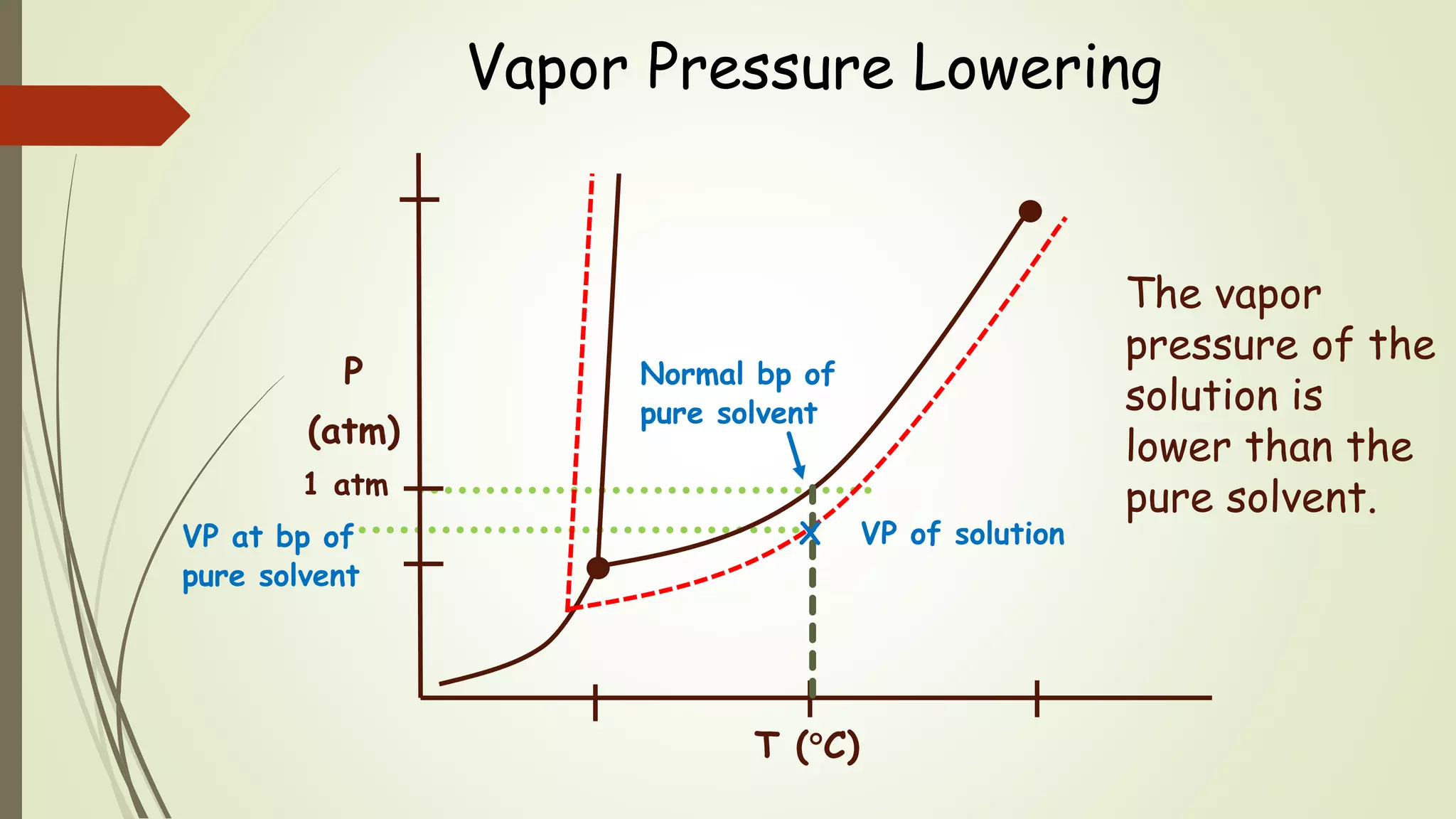
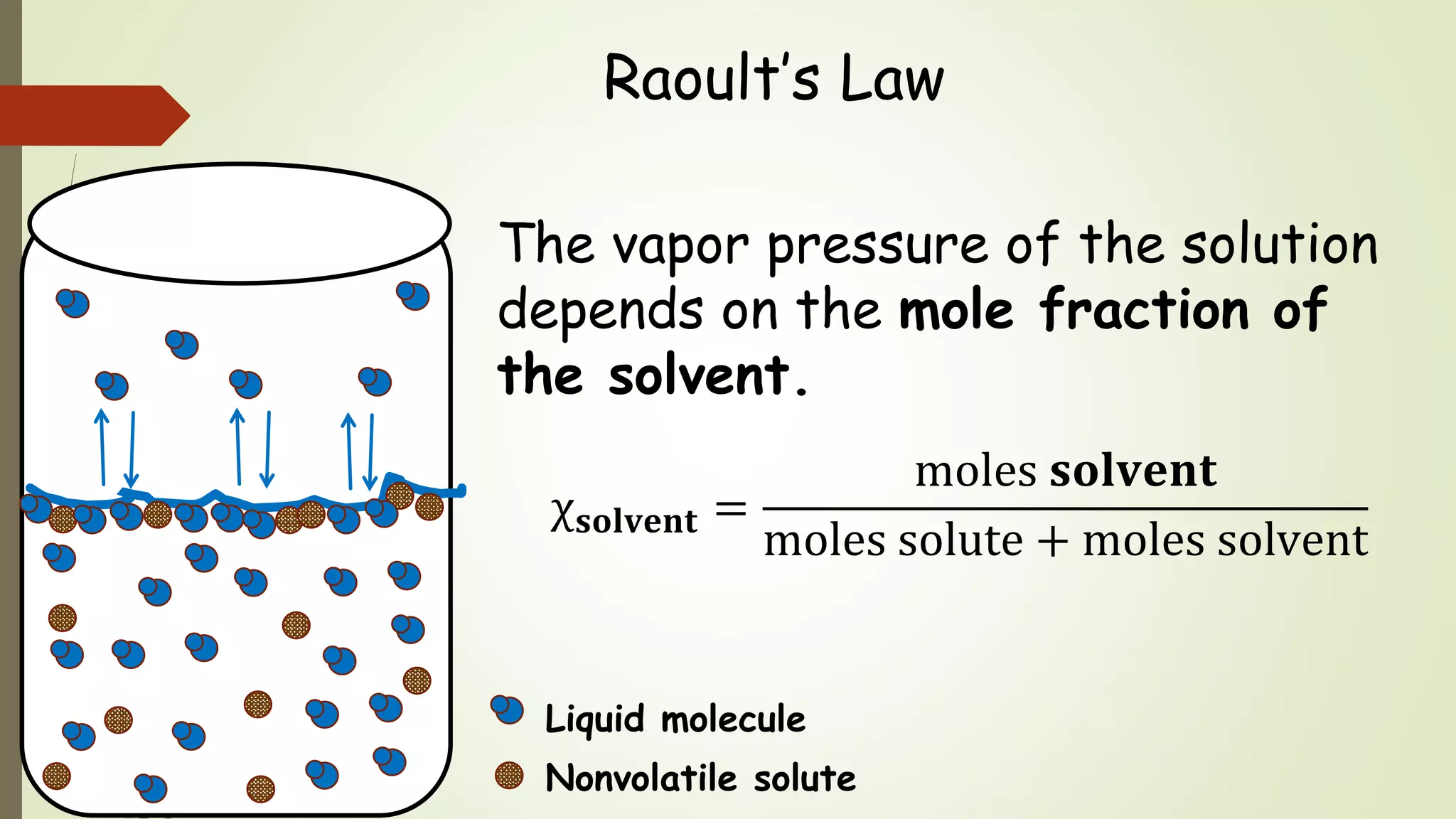
This document discusses colligative properties, which are physical properties of solutions that depend only on the ratio of solute to solvent particles and not the identity of the solute. It describes four colligative properties: boiling point elevation, freezing point depression, vapor pressure lowering, and osmotic pressure. It explains how adding a nonvolatile solute affects the phase diagram by shifting the freezing point downward and boiling point upward. Formulas are provided to calculate changes in boiling point and freezing point based on molality. Raoult's Law is introduced to explain how vapor pressure of a solution depends on the mole fraction of the solvent. Osmotic pressure is defined as the pressure required to prevent solvent flow across a semiperme

1. Colligative Properties
Pt. 3
By Shawn P. Shields, Ph.D.
This work is licensed by Shawn P. Shields-Maxwell under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0
International License.

2. Colligative Properties
A physical property of a solution that
depends only on the ratio of the number
of particles of solute to solvent in the
solution, not the identity of the solute.
Describes a nonvolatile solute dissolved
in a solvent.

3. Four Colligative Properties
Boiling point elevation
Freezing point depression
Vapor pressure lowering
Osmotic pressure
How can we explain these?

4. Recall: Pressure-Temperature Phase Diagrams
PT
TT
1 atm
vapor
liquid
solid
triple point
X mp X bp
T (C)
P
(atm)

5. Effect of Colligative Properties on the Phase Diagram
T (C)
P
(atm)
1 atm
Dotted lines
indicate the new
phase boundaries
for the solution.
The solid-liquid
coexistence line is
now shifted to
lower temperatures.
The liquid-vapor line
shifts to higher
temperatures.

6. Effect of Colligative Properties on the Phase Diagram
T (C)
P
(atm)
1 atm
new mp
X
new bp
X
Boiling point
elevation
Melting point
depression
Vapor pressure
lowering (come
back to this)

7. Boiling Point Elevation
Recall: The boiling point of a substance is the
temperature where the vapor pressure equals the
external (usually atmospheric) pressure.
The external pressure doesn’t change, but the
temperature required to attain that vapor pressure is
increased!
Tb = kbm
Tb is the increase in boiling
temperature
kbis the molal boiling point elevation
constant (look it up for a given
solvent)
m is the molality of the solute
molality =
moles solute
kg of solvent

8. Freezing Point Depression
When the freezing point is depressed, this means the
temperature must be lower before a given substance
freezes.
Tf = kfm
Tf is the decrease in freezing
temperature
kfis the molal freezing point
depression constant (look it up
for a given solvent)
m is the molality of the solute
molality (m) =
moles solute
kg of solvent

9. Calculating Solvent Mass
Use the volume of the solvent and its density to
find the mass of solvent for molality (m).
𝐦𝐨𝐥𝐚𝐥𝐢𝐭𝐲 (𝐦) =
𝐦𝐨𝐥𝐞𝐬 𝐬𝐨𝐥𝐮𝐭𝐞
𝐤𝐠 𝐨𝐟 𝐬𝐨𝐥𝐯𝐞𝐧𝐭
𝐝𝐞𝐧𝐬𝐢𝐭𝐲
𝐠
𝐦𝐋
=
𝐦𝐚𝐬𝐬
𝐯𝐨𝐥𝐮𝐦𝐞

10. Recall: Equilibrium Vapor Pressure
Molecules in the liquid phase
continuously vaporize and condense
in a closed container.
rate of evaporation = rate of condensation
The partial pressure of the gas is constant
at equilibrium.
Liquid molecule

11. Vapor Pressure Lowering
The vapor
pressure of the
solution is
lower than the
pure solvent.
T (C)
P
(atm)
1 atm
Normal bp of
pure solvent
VP at bp of
pure solvent
X VP of solution

12. Raoult’s Law
The vapor pressure of the solution depends on the
mole fraction of the solvent.
Psoln = χsolventPsolvent
ο
Psoln is the vapor pressure of the solution
 is the mole fraction of the solvent
Psolvent
ο
is the vapor pressure of the pure solvent

13. Raoult’s Law
The vapor pressure of the solution
depends on the mole fraction of
the solvent.
χ 𝐬𝐨𝐥𝐯𝐞𝐧𝐭 =
moles 𝐬𝐨𝐥𝐯𝐞𝐧𝐭
moles solute + moles solvent
Liquid molecule
Nonvolatile solute

14. Osmosis
The two regions are
separated by a
semipermeable membrane
that allows solvent to pass,
but not solute particles.
Osmosis By OpenStax College [CC BY 3.0
(http://creativecommons.org/licenses/by/3.0)], via Wikimedia Commons
The net movement of solvent molecules from a
region of lower solute concentration to one with a
higher concentration.

15. Osmotic Pressure ()
Osmotic pressure is the amount of pressure required to
stop the flow of solvent.
A similar equation to the Ideal Gas law can be written for
the osmotic pressure:
Π V = nRT
Where  is the osmotic pressure (in the same units as
the gas constant, R)
V is the volume in L, n is moles of solute, and
T is temperature in K

16. Osmotic Pressure ()
We can rearrange this equation to a more
useful form
Π V = nRT
Π =
n
V
RT = CRT
Where C is the concentration (M, molarity)

17. Example Problems
will be posted separately.