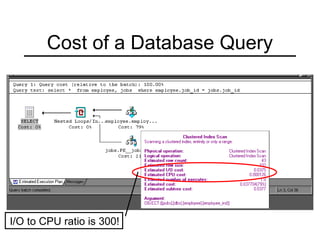
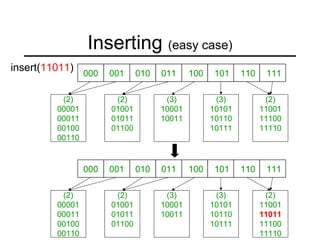
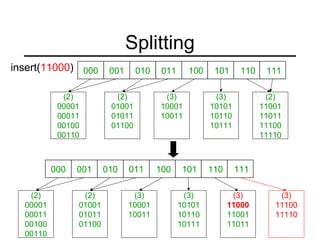
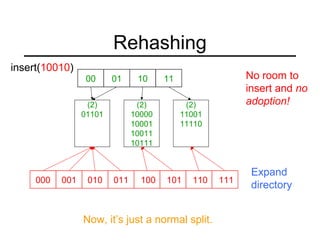
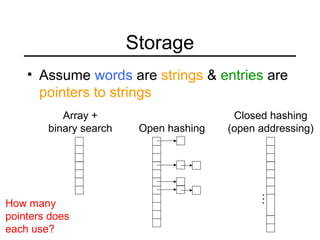
This document summarizes key points about extendible hashing and discusses its use for a spelling dictionary case study. Extendible hashing is a hashing technique that optimizes disk accesses for huge datasets by storing hash buckets in disk blocks. It uses a directory to hash to the correct bucket. The document explains how to insert keys, split buckets, and rehash the table. It also discusses solutions for the spelling dictionary case study, comparing storage and time efficiency of sorted arrays, open hashing, and closed hashing with linear probing.