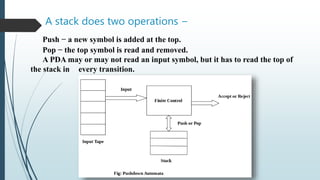
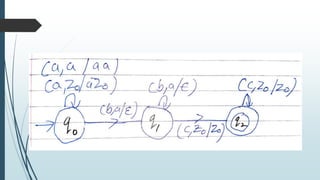
The document discusses pushdown automata (PDA), which are more powerful than finite automata (FA) as they can accept languages that FA cannot. A PDA comprises a finite state machine and an infinite-size stack, with operations to push and pop symbols. It describes the components of deterministic PDAs (DPDA) and non-deterministic PDAs (NPDA), emphasizing their structural differences.

1. Topic :- Pushdown Automata
Name :- Ashish Duggal
Qualification :- M.C.A.

2. Pushdown Automata Introduction
 A PDA is more powerful than FA. Any language which can be acceptable by
FA can also be acceptable by PDA. PDA also accepts a class of language which
even cannot be accepted by FA. Thus PDA is much more superior to FA.
 Basically a pushdown automaton is − "Finite state machine" + "a stack"
 A pushdown automaton has three components −
an input tape,
a control unit, and
a stack with infinite size.
The stack head scans the top symbol of the stack.

3. A stack does two operations −
Push − a new symbol is added at the top.
Pop − the top symbol is read and removed.
A PDA may or may not read an input symbol, but it has to read the top of
the stack in every transition.

4. 7 Components of DPDA
 M = (Q, Σ, Γ, δ, q0, Z0, F), where
 Q — finite set of states
 Σ — finite input alphabet
 Γ — finite alphabet of pushdown symbols
 q0 ∈ Q — starting/initial state
 Z0 ∈ Γ — start symbol on the pushdown
 F ⊆ Q — set of final states
 δ — mapping Q × (Σ ∪ {ε}) × Γ → Q×Γ

5. 7 Components of NON-DPDA / NPDA
 M = (Q, Σ, Γ, δ, q0, Z0, F), where
 Q — finite set of states
 Σ — finite input alphabet
 Γ — finite alphabet of pushdown symbols
 δ —transition function -> Q × (Σ ∪ {ε}) × Γ → 2 ^(Q×Γ )
 q0 ∈ Q — starting/initial state
 Z0 ∈ Γ — start symbol on the pushdown
 F ⊆ Q — set of final states

6. Example

8. Thank You