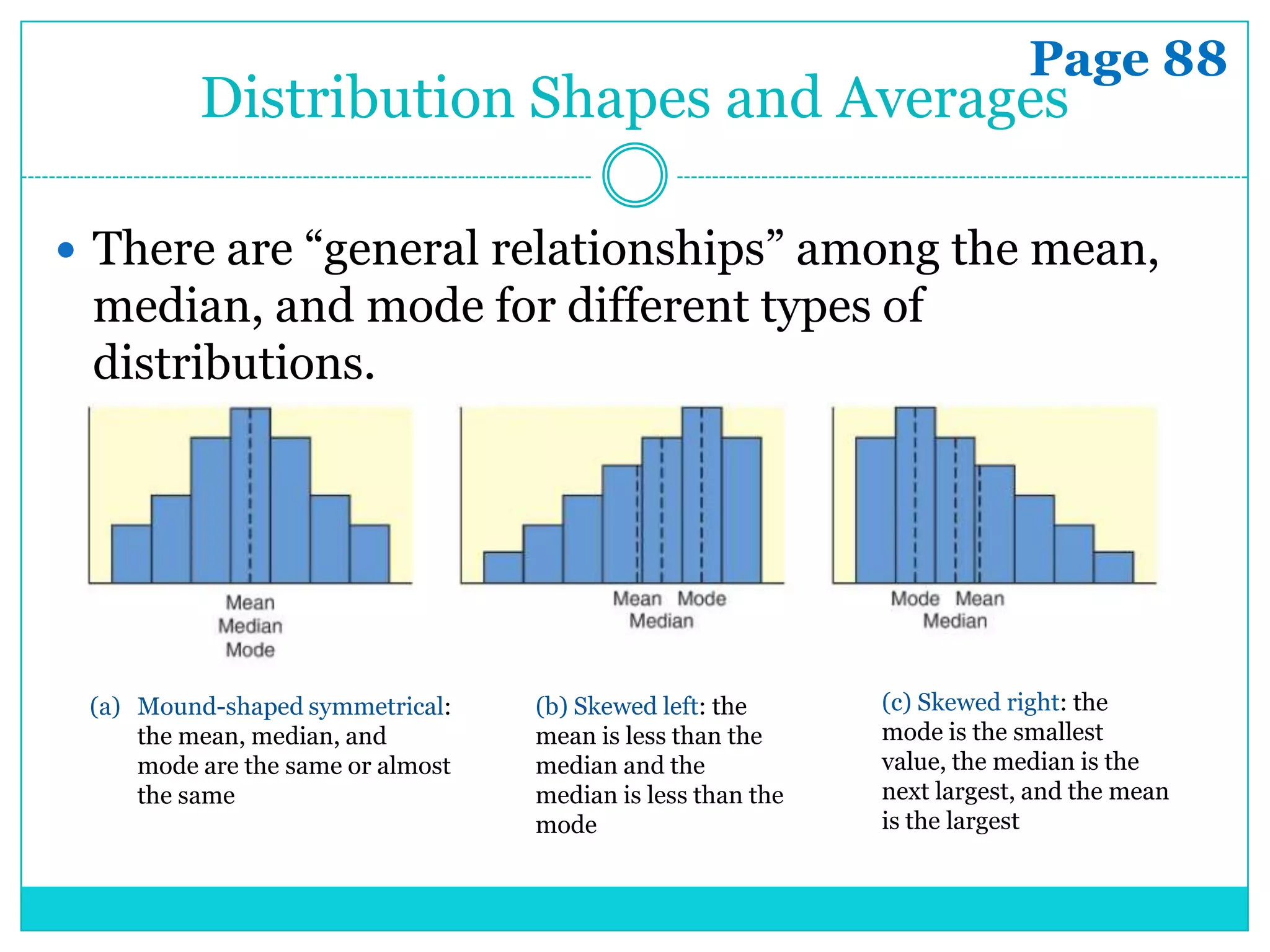
This document discusses different measures of central tendency including the mode, median, and mean. It provides definitions and explanations of how to calculate each one. The mode is the most frequently occurring value, the median is the middle value of an ordered data set, and the mean is the average found by summing all values and dividing by the number of values. The document contrasts these measures and discusses which to use based on the measurement level of the data and shape of the distribution. It also provides examples of how to interpret the mean and median when comparing multiple data sets. Homework problems are assigned from the text.

1. 3.1 Measures of Central Tendency:
Mode, Median, and Mean
CHAPTER 3
AVERAGES AND VARIATION

2. Page 82
Averages
 An average is a single number used to describe an
entire sample or an entire population.
 There are many ways to compute averages, but we will study
only three of the major ones.
 Mode, Median, and Mean

3. Page 82
Mode
 The mode of a data set is the value that occurs most
frequently.
 The easiest average to compute
 For larger data sets, it is useful to order—or sort—the data
before scanning them for the mode.
 Not every data set has a mode
 The mode is not very stable. Changing just one number in a
data set can change the mode dramatically.
 The mode is a useful average when we want to know the most
frequently occurring data value

4. Page 83
Median
 The median is the central value of an ordered
distribution.
 The median uses the position rather than the specific value of
each data entry.
 If the extreme values of a data set change, the median usually
does not change.
 Advantage: if a data set contains an outlier, the median may be
a better indicator of the center
 Disadvantage: not sensitive to the specific size of a data value

5. Median
 To find the median:
1. Order the data from smallest to largest
2. For an odd number of data values in the distribution:
3. For an even number of data values in the distribution:
To find the middle of a large data set:

6. Page 85
Mean
 The mean is an average that uses the exact value of
each entry is the mean (sometimes called the
arithmetic mean).
 The most important/frequently used ―average‖
 When the sample size is large and does not include outliers,
the mean score usually provides a better measure of central
tendency.
 Disadvantage: it can be affected by exceptional values/outliers

7. Mean
 To compute the mean: add the values of all the
entries and then divide by the number of entries.

8. Note AP Formula Sheet!
Mean
∑ is the Greek
 Notation letter S called
 Let x represent any value in the data set ―sigma‖
 The summation symbol ∑ means ―sum the following‖
 ∑x (read ―the sum of all given x values‖) means add up all the x
values
The mean of a sample is called ―x bar‖ The mean of a population is called ―mu‖
n = number of data values in the sample N = number of data values in the sample
μ is the Greek
letter mu called
―mew‖

9. Using the Calculator
 The TI-83 and TI-84 make it fairly easy to find the
mode, median, and mean.
1. Enter the data values in L1
2. Hit STAT, choose 2:SortA to organize the data
3. View the list to find the mode
4. Hit STAT, tab over to CALC, choose 1:1 – Var Stats, Hit 2nd 1
ENTER
Because the formulas for
the sample mean and the
population mean are the
same, this feature is used
to find, μ. It is YOUR job
to know if you are
working with a sample or
a population.

10. Mean and Median
 The mean and median of two key measures of center.
 Important for comparing data sets
 State what the values are AND what they tell us about each set or one
set compared to the other
 Important for describing data sets
 Gives a ―typical‖ number to consider when looking at any data sets
 For Example:
 Consider two data sets A and B where they are both roughly normal
(bell-shaped) and have about the same spread. The mean of A is 6
and the mean of B is 4.
 You might say: ―Set A is centered at 6, where set B is centered at 4.
Since the mean of set B is lower than set A, set B would have lower
overall values, on average than set A‖

11. Page 86
Resistant Measures
 A resistant measure is one that is not influenced
by extremely high or low data values.
 The mean is not a resistant measure of center because
changing the size of only one data value will affect the mean
and it is affected by outliers.
 The mean is an example of a non-resistant measure.
 The median is more resistant to changes in individual data
values and outliers.

12. Page 87
Data Types and Averages
 Levels of Measurement: nominal, ordinal, interval,
and ratio
 The mode (if it exists) can be used with all four levels
 The median can be used with data at the ordinal level of above.
 The mean can be used with data at the interval or ratio level
(there are some exceptions at the ordinal level).
 Be careful with taking the average of averages!
 We need to know the sample size used to find each individual
average

13. Page 88
Distribution Shapes and Averages
 There are ―general relationships‖ among the mean,
median, and mode for different types of
distributions.
(a) Mound-shaped symmetrical: (b) Skewed left: the (c) Skewed right: the
the mean, median, and mean is less than the mode is the smallest
mode are the same or almost median and the value, the median is the
the same median is less than the next largest, and the mean
mode is the largest

14. Homework
 Page 89
 #1, 2, 3, 6, 7, 8, 14
 #17 Parts a, b, & c only
 #18