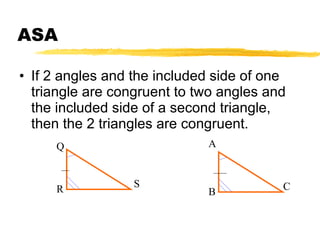
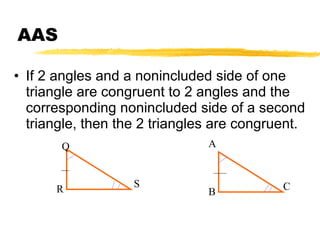
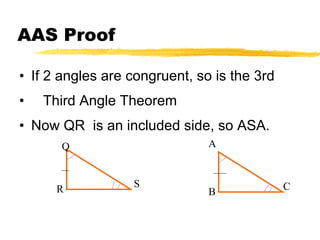
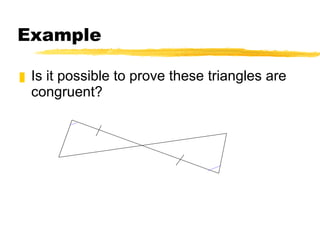
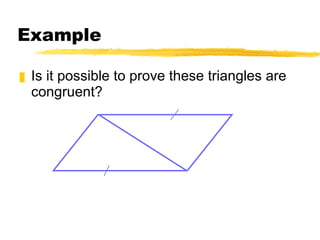
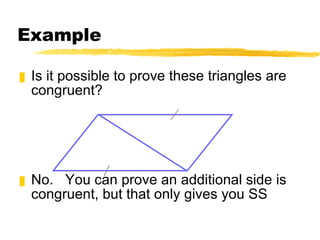
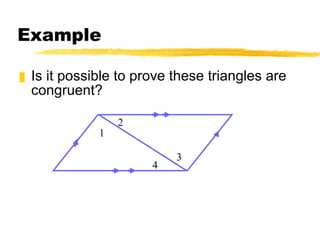
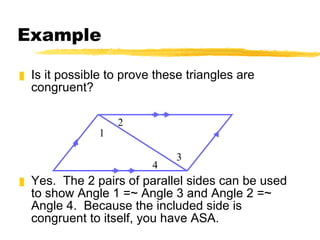
This document summarizes the ASA and AAS postulates for proving triangle congruence. It states that if two angles and the included side of one triangle are congruent to those of another triangle, they are congruent by ASA. If two angles and a non-included side are congruent, they are congruent by AAS. It provides examples of applying these postulates to determine if triangles can be proven congruent and includes a word problem about using angles to locate a meteorite.

1. 4.4 Proving Triangles are Congruent: ASA and AAS Objectives: - Prove that triangles are congruent using ASA and AAS

2. ASA If 2 angles and the included side of one triangle are congruent to two angles and the included side of a second triangle, then the 2 triangles are congruent. A B C Q R S

3. AAS If 2 angles and a nonincluded side of one triangle are congruent to 2 angles and the corresponding nonincluded side of a second triangle, then the 2 triangles are congruent. A B C Q R S

4. AAS Proof If 2 angles are congruent, so is the 3rd Third Angle Theorem Now QR is an included side, so ASA. A B C Q R S

5. Example Is it possible to prove these triangles are congruent?

6. Example Is it possible to prove these triangles are congruent? Yes - vertical angles are congruent, so you have ASA

7. Example Is it possible to prove these triangles are congruent?

8. Example Is it possible to prove these triangles are congruent? No. You can prove an additional side is congruent, but that only gives you SS

9. Example Is it possible to prove these triangles are congruent? 1 2 3 4

10. Example Is it possible to prove these triangles are congruent? Yes. The 2 pairs of parallel sides can be used to show Angle 1 =~ Angle 3 and Angle 2 =~ Angle 4. Because the included side is congruent to itself, you have ASA. 1 2 3 4

11. Meteorite example Page 222 describes a meteor sighting. 2 witnesses saw the meteor from different locations and recorded the angle. When you draw these sightlines, you know where to look for the meteor. How important is accuracy? If the angles were off by 2˚ in either direction, the location would lie in a 25 square mile area.

12. Do p. 223 2-13, 28 Quiz tomorrow Homework: worksheets