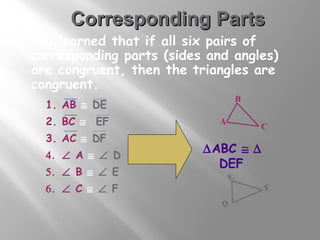
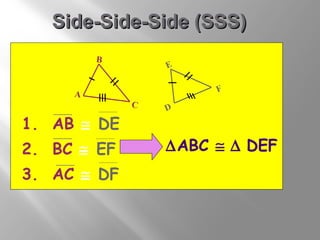
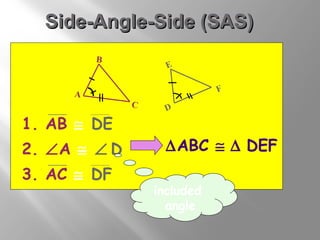
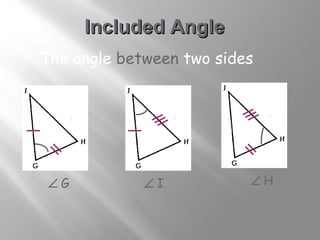
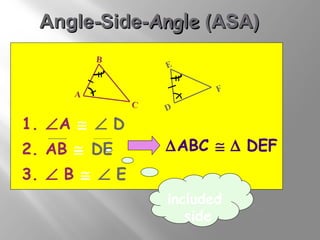
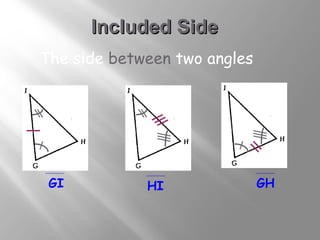
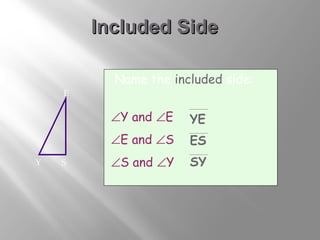
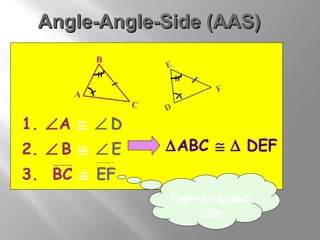
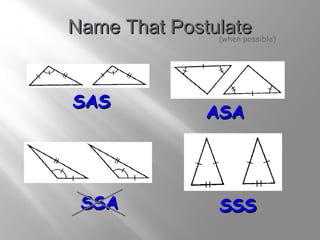
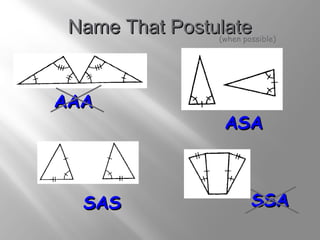
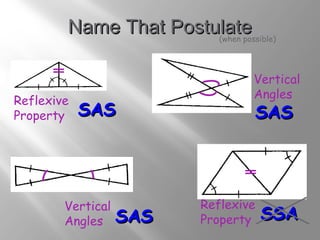
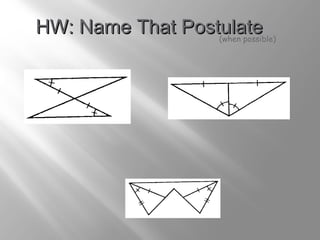
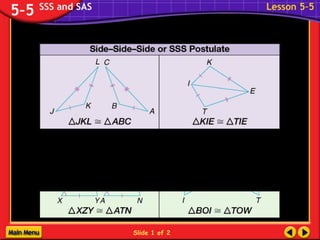
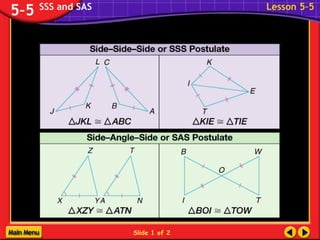
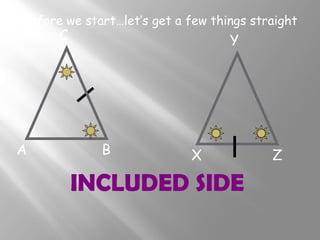
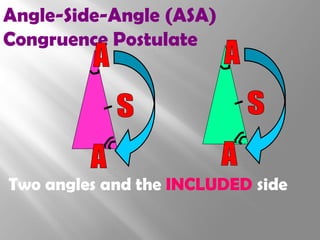
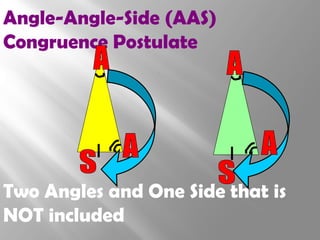
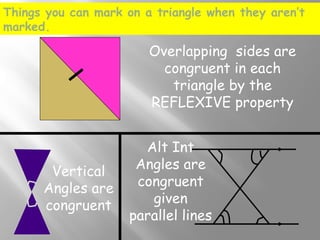
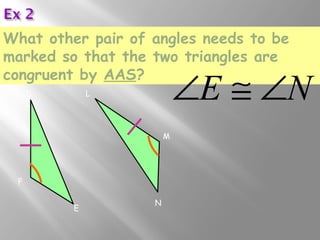
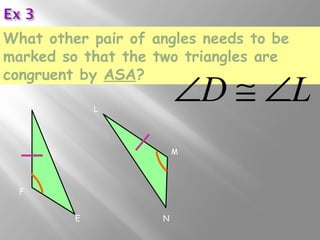
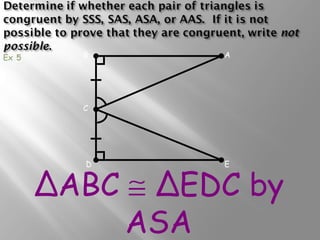
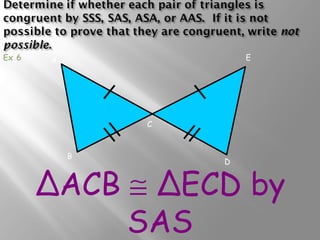
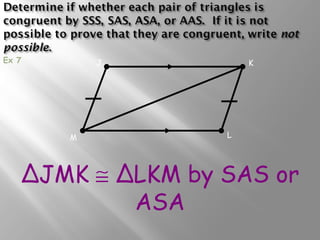
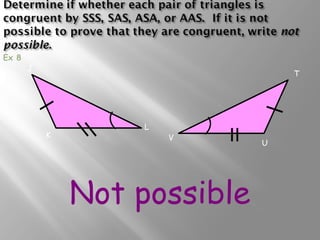
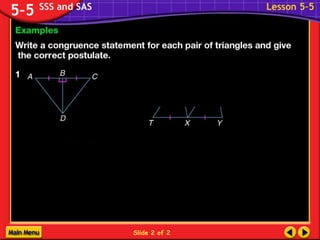
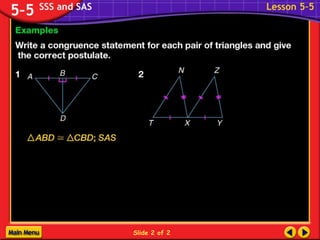
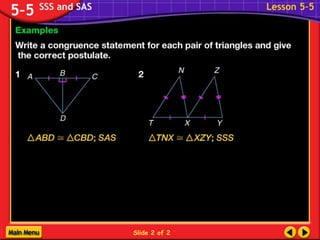
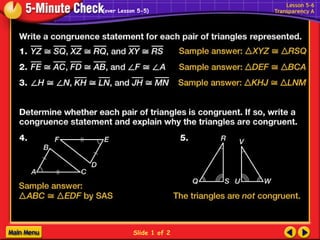
The document discusses congruence postulates for triangles. It explains that two triangles are congruent if they meet the criteria of Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), or Angle-Angle-Side (AAS). The document provides examples of applying these postulates to determine if triangles are congruent and identifies the additional information needed.

3. TThhee IIddeeaa ooff aa CCoonnggrruueennccee
Two geometric figures with
exactly the same size and
shape.
B
A C
F
E D

4. HHooww mmuucchh ddoo yyoouu
nneeeedd ttoo kknnooww.. .. ..
. . . about two triangles
to prove that they
are congruent?

5. CCoorrrreessppoonnddiinngg PPaarrttss
You learned that if all six pairs of
corresponding parts (sides and angles)
are congruent, then the triangles are
congruent.
B
A C
DABC @ D
DEF
E
D F
1. AB @ DE
2. BC @ EF
3. AC @ DF
4. Ð A @ Ð D
5. Ð B @ Ð E
6. Ð C @ Ð F

6. DDoo yyoouu nneeeedd aallll ssiixx ??
NO !
SSS
SAS
ASA
AAS

7. SSiiddee--SSiiddee--SSiiddee ((SSSSSS))
1. AB @ DE
2. BC @ EF
3. AC @ DF
DABC @ D DEF
B
A C
E
D F

8. SSiiddee--AAnnggllee--SSiiddee ((SSAASS))
1. AB @ DE
2. ÐA @ Ð D
3. AC @ DF
DABC @ D DEF
B
A C
E
D F
included
angle

9. IInncclluuddeedd AAnnggllee
The angle between two sides
Ð G Ð I Ð H

10. IInncclluuddeedd AAnnggllee
Name the included angle:
YE and ES
ES and YS
YS and YE
E
Y S
Ð E
Ð S
Ð Y

11. AAnnggllee--SSiiddee--AAnnggllee ((AASSAA))
1. ÐA @ Ð D
2. AB @ DE
3. Ð B @ Ð E
DABC @ D DEF
B
A C
E
D F
included
side

12. IInncclluuddeedd SSiiddee
The side between two angles
GI HI GH

13. IInncclluuddeedd SSiiddee
Name the included side:
ÐY and ÐE
ÐE and ÐS
ÐS and ÐY
E
Y S
YE
ES
SY

14. AAnnggllee--AAnnggllee--SSiiddee ((AAAASS))
1. ÐA @ Ð D
2. Ð B @ Ð E
3. BC @ EF
DABC @ D DEF
B
A C
E
D F
Non-included
side

15. WWaarrnniinngg:: NNoo SSSSAA PPoossttuullaattee
B
There is no such
thing as an SSA
postulate!
A C
E
D
F
NOT CONGRUENT

16. WWaarrnniinngg:: NNoo AAAAAA PPoossttuullaattee
B
A C
E
D
F
There is no such
thing as an AAA
postulate!
NOT CONGRUENT

17. TThhee CCoonnggrruueennccee PPoossttuullaatteess
SSS correspondence
ASA correspondence
SAS correspondence
AAS correspondence
SSA correspondence
AAA correspondence

18. NNaammee TThhaatt PPoossttuullaattee
(when possible)
SSAASS AASSAA
SSSSAA SSSSSS

19. NNaammee TThhaatt PPoossttuullaattee (when possible)
AASSAA
AAAAAA
SSAASS
SSSSAA

20. NNaammee TThhaatt PPoossttuullaattee (when possible)
Reflexive
SSAASS
SSAASS SSAASS
Property
Vertical
Angles
Vertical
Angles
Reflexive
Property SSSSAA

21. HHWW:: NNaammee TThhaatt PPoossttuullaattee (when possible)

22. HHWW:: NNaammee TThhaatt PPoosstt(uuwhlleaan pttoseesible)

23. LLeett’’ss PPrraaccttiiccee
Indicate the additional information needed
to enable us to apply the specified
congruence postulate.
For ASA:
For SAS:
ÐB @ ÐD
AC @ FE
For AAS: ÐA @ ÐF

24. HHWW
Indicate the additional information needed
to enable us to apply the specified
congruence postulate.
For ASA:
For SAS:
For AAS:

25. A
B
F
C
E
D

26. Slide 1 of 2

27. Slide 1 of 2

28. Before we start…let’s get a few things straight
A B
Y
INCLUDED SIDE
C
X Z

29. Angle-Side-Angle (ASA)
Congruence Postulate
Two angles and the INCLUDED side

30. Angle-Angle-Side (AAS)
Congruence Postulate
Two Angles and One Side that is
NOT included

31. }Your Only Ways
To Prove
Triangles Are
Congruent

32. Things you can mark on a triangle when they aren’t
marked.
Overlapping sides are
congruent in each
triangle by the
REFLEXIVE property
Vertical
Angles are
congruent
Alt Int
Angles are
congruent
given
parallel lines

33. ΔDEF ΔLMN Ð D @ Ð N DE @
NL
Ð @ Ð
In and , , and
E L
. Write a congruence statement.
D D E F @ D N L M

34. What other pair of angles needs to be
marked so that the two triangles are
congruent by AAS?
F
D
E
M
L
N
ÐE @ ÐN

35. What other pair of angles needs to be
marked so that the two triangles are
congruent by ASA?
F
D
E
M
L
N
ÐD @ ÐL

36. ΔGIH @ ΔJIK by
AAS
G
I
H J
K
Ex 4

37. B A
ΔABC @ ΔEDC by
ASA
C
D E
Ex 5

38. ΔACB @ ΔECD by
SAS
B
A
C
E
D
Ex 6

39. J K
M L
ΔJMK @ ΔLKM by SAS or
ASA
Ex 7

40. Not possible
K
J
L
T
U
Ex 8
V

41. Slide 2 of 2

42. Slide 2 of 2

43. Slide 2 of 2

44. Slide 2 of 2

45. (over Lesson 5-5)
Slide 1 of 2

46. (over Lesson 5-5)
Slide 1 of 2

47. Slide 1 of 2

48. Slide 1 of 2

49. Slide 1 of 2

50. Slide 1 of 2

51. Slide 2 of 2

52. Slide 2 of 2

53. Slide 2 of 2

54. Slide 2 of 2

55. All rights belong to their respective
owners.
Copyright Disclaimer Under Section 107
of the Copyright Act 1976, allowance is
made for "fair use" for purposes such as
criticism, comment, news reporting,
TEACHING, scholarship, and research.
Fair use is a use permitted by copyright
statute that might otherwise be
infringing.
Non-profit, EDUCATIONAL or personal
use tips the balance in favor of fair use.