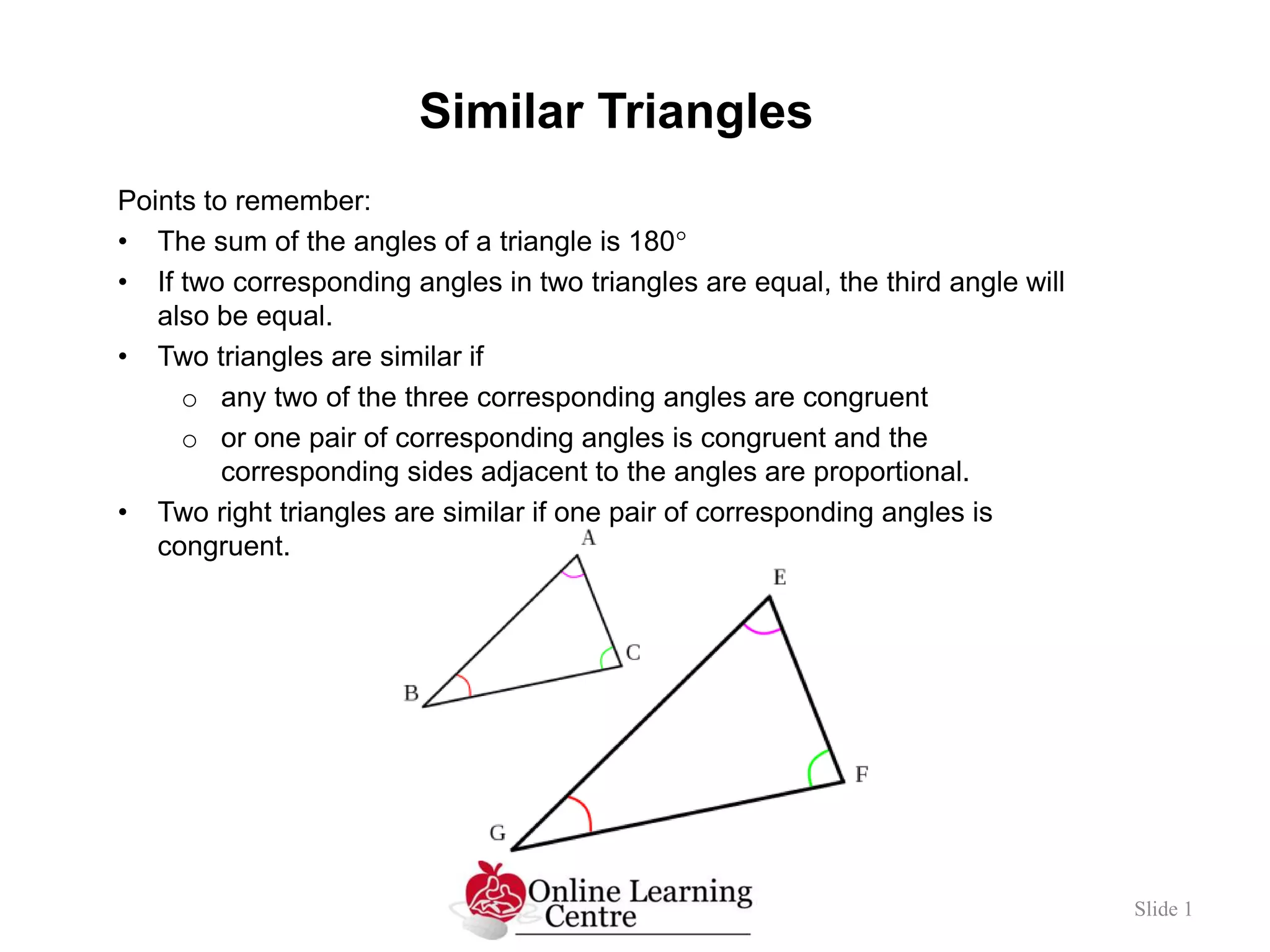
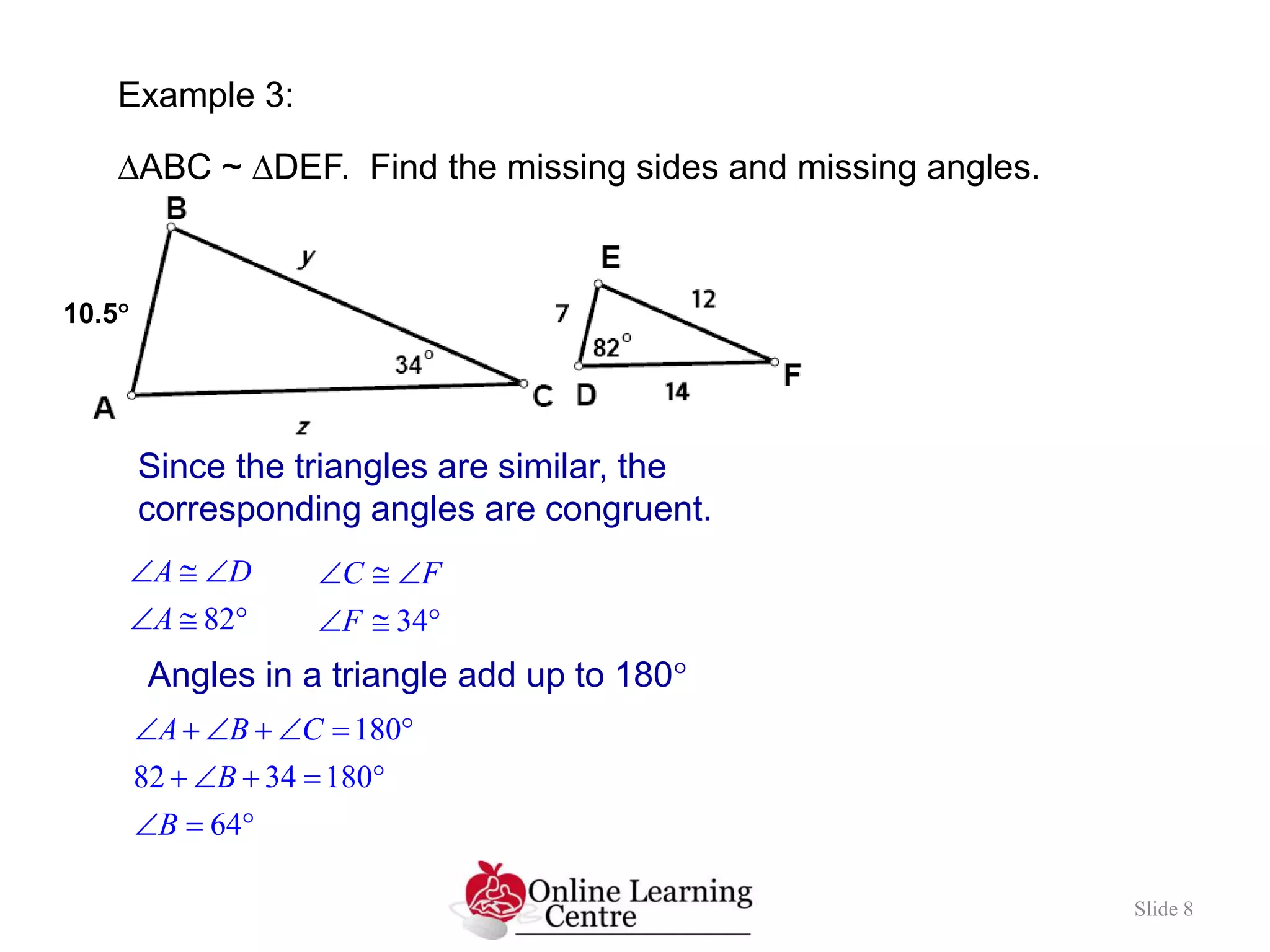
- The document discusses similar triangles and provides examples of finding missing side lengths and angles of similar triangles using proportional reasoning. - Similar triangles are defined as triangles where corresponding angles are congruent or corresponding sides are proportional. - Examples show setting up proportions between corresponding sides or angles of similar triangles to calculate missing values. One example finds the height of a tree using similar right triangles formed by a person's view in a mirror.

1. Similar Triangles
Slide 1
Points to remember:
• The sum of the angles of a triangle is 180
• If two corresponding angles in two triangles are equal, the third angle will
also be equal.
• Two triangles are similar if
o any two of the three corresponding angles are congruent
o or one pair of corresponding angles is congruent and the
corresponding sides adjacent to the angles are proportional.
• Two right triangles are similar if one pair of corresponding angles is
congruent.

2. Slide 2
Example 1:
If DCE ~ VUW, find the measure of .CD

3. Slide 3
Example 1:
If DCE ~ VUW, find the measure of .CD
List the corresponding sides:
and
and
and
DC VU
DE VW
CE UW

4. Slide 4
Example 1:
If DCE ~ VUW, find the measure of .CD
List the corresponding sides:
and
and
and
DC VU
DE VW
CE UW
Set up the proportion and solve…
12 9
36 x

12 324x 
1
12 12
2 324x

27x 
OR
36
12 9
x

324 12x
3
12 12
24 12x

27x 

5. Slide 5
Example 2:
The triangles are similar. Calculate the missing side.
If 42 and 30, then 12FH RH FR  
12
Let x = length of 𝐹𝑆
12
84 42
x

42 1008x 
42 10
42 42
08x

24x 

6. Slide 6
Example 2:
The triangles are similar. Calculate the missing side.
If 42 and 30, then 12FH RH FR  
12
Let x = length of 𝐹𝑆
12
84 42
x

42 1008x 
42 10
42 42
08x

24x 
24
FS SG FG 
24 84SG 
60SG 
Answer:
The missing side has a measure of 60.

7. Slide 7
10.5
Example 3:
ABC ~ DEF. Find the missing sides and missing angles.

8. Slide 8
10.5
Example 3:
ABC ~ DEF. Find the missing sides and missing angles.
Since the triangles are similar, the
corresponding angles are congruent.
82
A D
A
  
   34
C F
F
  
  
Angles in a triangle add up to 180
180
82 34 180
64
A B C
B
B
      
    
  

9. Slide 9
10.5
Example 3:
ABC ~ DEF. Find the missing sides and missing angles.
Since the triangles are similar, the
corresponding angles are congruent.
82
A D
A
  
   34
C F
F
  
  
Angles in a triangle add up to 180
180
82 34 180
64
A B C
B
B
      
    
  
Corresponding sides
are proportional.
Set up the proportion…
10.5
7 12
y

7 126y 
18y 
10.5
7 14
z

7 147z 
21z 

10. Slide 10
Example 4:
Tom wants to find the height of a tall evergreen tree. He places a
mirror on the ground and positions himself so that he can see the
reflection of the top of the tree in the mirror. The mirror is 0.7 m
away from him and 5.5 m from the tree. If Tom is 1.8 m tall, how tall
is the tree? Note: the triangles are similar.

11. Set up the proportion and solve…
Slide 11
Example 4:
Tom wants to find the height of a tall evergreen tree. He places a
mirror on the ground and positions himself so that he can see the
reflection of the top of the tree in the mirror. The mirror is 0.7 m
away from him and 5.5 m from the tree. If Tom is 1.8 m tall, how tall
is the tree? Note: the triangles are similar.
Answer:
The tree would be 14.14 m tall.
1.8 0.7
5.5h

0.7 9.9h 
0.7
0.7 9
.7
.9
0
h

14.14h 