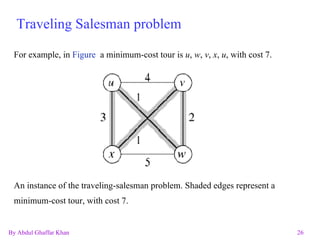
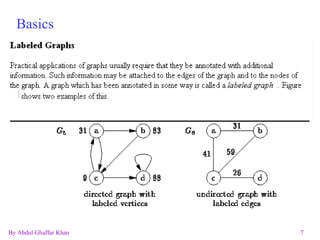
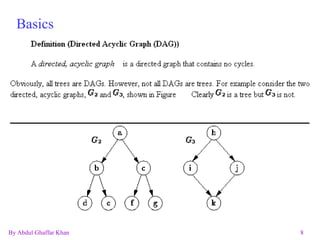
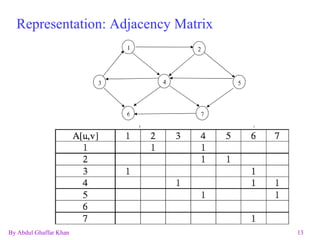
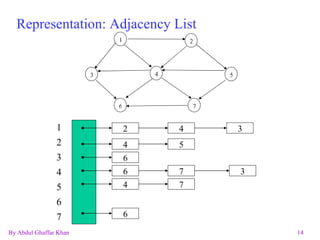
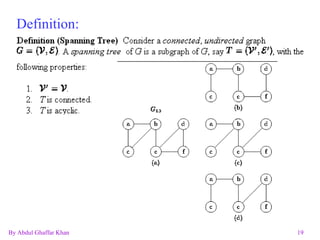
The document discusses various graph data structures and algorithms. It defines directed and undirected graphs, and methods for representing graphs using adjacency matrices and adjacency lists. It then explains algorithms for finding shortest paths, spanning trees, minimum spanning trees, and solving the traveling salesman problem in graphs.

1. Graph ADT BY Abdul Ghaffar Khan

2. Contents Basics Representation of of Graph ADT Shortest Path Algorithm Spanning Tree Minimal Spanning Tree Traveling Salesman problem

3. Basics

4. Basics: Definition (Directed Graph) A directed graph , or digraph , is an ordered pair with the following properties: The first component, , is a finite, non-empty set. The elements of are called the vertices of G . The second component, , is a finite set of ordered pairs of vertices. That is, . . The elements of are called the edges of G . For example, consider the directed graph comprised of four vertices and six edges : If pair is the pair is not ordered then it becomes only a Graph but not Directed.

5. Basics

6. Basics

7. Basics

8. Basics

9. Basics

10. Basics

11. Basics

12. Basics

13. Representation: Adjacency Matrix 1 2 3 6 7 5 4

14. Representation: Adjacency List 1 2 3 4 5 6 7 2 4 3 4 5 7 6 7 4 3 6 6 1 2 3 6 7 5 4

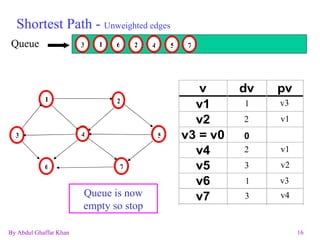
15. Shortest Path Unweighted edges Q.Enqueue(v0); while (!Q.IsEmpty) { V = Q.Dequeue(); for (Each W adjacent to V) if (T[W].Dist == Maxint) { T[W].Dist = T[V].Dist + 1; T[W].Path = V; Q.Enqueue(W); } } Breadth First Search Algorithm

16. Shortest Path - Unweighted edges Queue Enqueue Vo Ignore V4 V4 != MaxInt Ignore V6 V6 != MaxInt Ignore V4 V4 != MaxInt Ignore V7 V7 != MaxInt Ignore V6 V6 != MaxInt Queue is now empty so stop 1 2 3 6 7 5 4 3 6 1 v3 1 1 v3 4 2 v1 2 v1 2 No vertices adjacent to 6 5 v2 3 7 3 v4

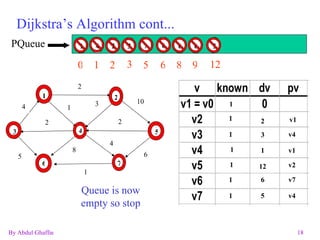
17. Dijkstra’s Algorithm Q.Enqueue(v0); while (!Q.IsEmpty) { do { V = Q.Dequeue(); while (T[V].Known); T[V].Known = true; for (Each W adjacent to V) if(T[W].Dist > T[V].Dist + C(V,W) { T[W].Dist = T[V].Dist + C(V,W); T[W].Path = V; Q.Enqueue(W); } } Only accept unknown edges Modify the path if an improvement to dv exists

18. Dijkstra’s Algorithm cont... 1 2 3 6 7 5 4 4 4 1 1 2 2 2 3 6 5 10 8 PQueue No improvement to v4 so skip No improvement to v1 so skip No improvement to v4 so skip No improvement to v7 so skip Queue is now empty so stop Enqueue Vo 1 0 4 1 1 v1 2 2 2 v1 1 1 3 3 3 v4 7 5 v4 5 6 9 v4 9 1 5 12 v2 12 1 8 v3 6 8 Update dv and pv to reflect improvement 1 6 6 Update dv and pv to reflect improvement v7 6 1 V6 is already known so ignore 1

19. Definition:

20. Definition:

21. Prim’s Algorithm Basic Idea 1. Build a tree starting at Vo=u. 2. Select vertex v which is closest to u and add (u,v) to tree. 3. Find next closes vertex v to tree and add. Repeat 3 Until all v have been consumed.

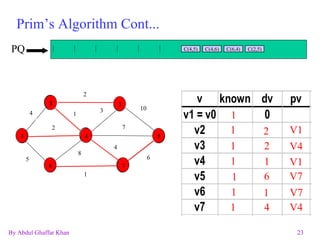
22. Prim’s Algorithm Q.Enqueue(V 0 ,V 0 ); Vertices=1 while (Vertices++ < |V|) { do { E = Q.Dequeue(); while (T[v].Known); T[v].Known = true; for (Each w adjacent to v) if(T[w].Dist > C(v,w) && !T[w].known){ T[w].Dist = C(v,w); T[w].Path = v; Q.Enqueue(v,w); } } Very Similar to Dijkstra’s Algorithm. dv now only holds the edge weight. PQ of edges c(u,v), where u is in the tree and v is not. Where E = (u,v)

23. Prim’s Algorithm Cont... C(1,1) PQ 1 2 3 6 7 5 4 4 4 1 2 7 2 3 6 5 10 8 1 1 1 C(1,4) C(1,2) C(1,3) 1 4 1 V1 C(4,1) C(1,2) C(4,3) C(4,2) C(4,6) C(1,3) C(4,7) C(4,5) 2 1 2 V1 C(2,4) C(2,1) C(4,3) C(4,2) C(4,6) C(1,3) C(4,7) C(4,5) C(2,5) 3 1 2 V4 C(2,4) C(3,4) C(2,1) C(4,2) C(4,6) C(1,3) C(4,7) C(4,5) C(2,5) C(3,1) C(3,6) 4 V4 7 1 C(4,6) C(4,5) C(2,5) C(3,1) C(3,6) C(7,5) C(7,4) C(7,6) 6 1 1 V7 C(4,6) C(4,5) C(2,5) C(3,1) C(3,6) C(7,5) C(7,4) C(6,7) C(6,3) C(6,4) 5 1 6 V7

24. Prim’s Algorithm Cont.. The Algorithm stops when we have accepted |V| vertices. We can read the accepted edges from the table directly.

25. Traveling Salesman problem The traveling-salesman problem , which is closely related to the Hamiltonian-cycle problem, a salesman must visit n cities. Modeling the problem as a complete graph with n vertices, we can say that the salesman wishes to make a tour , or Hamiltonian cycle, visiting each city exactly once and finishing at the city he starts from. There is an integer cost c ( i , j ) to travel from city i to city j , and the salesman wishes to make the tour whose total cost is minimum, where the total cost is the sum of the individual costs along the edges of the tour.

26. Traveling Salesman problem For example, in Figure a minimum-cost tour is u , w , v , x , u , with cost 7. An instance of the traveling-salesman problem. Shaded edges represent a minimum-cost tour, with cost 7.