Shortest path

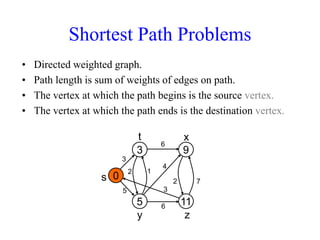
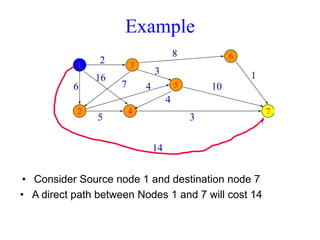
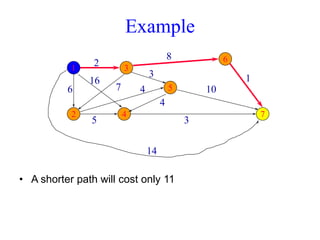
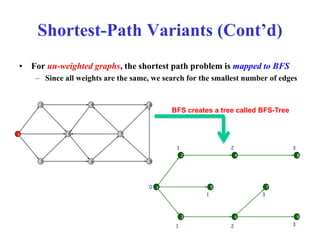
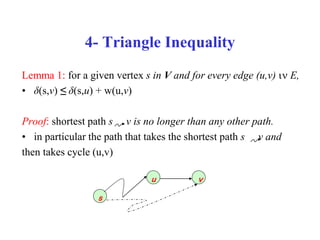
Shortest Path Problems
• Directed weighted graph.
• Path length is sum of weights of edges on path.
• The vertex at which the path begins is the source vertex.
• The vertex at which the path ends is the destination vertex.
0
3 9
5 11
3
6
5
7
6
s
t x
y z
2
2 1
4
3

Example
1
2
3
4
5
6
7
2
6
16
7
8
10
3
14
4
4
5 3
1
1
7
• Consider Source node 1 and destination node 7
• A direct path between Nodes 1 and 7 will cost 14

Example
1
2
3
4
5
6
7
2
6
16
7
8
10
3
14
4
4
5 3
1
• A shorter path will cost only 11

Shortest-Path Variants
• Single-source single-destination (1-1): Find the shortest
path from source s to destination v.
• Single-source all-destination(1-Many): Find the shortest
path from s to each vertex v.
• Single-destination shortest-paths (Many-1): Find a shortest
path to a given destination vertex t from each vertex v.
• All-pairs shortest-paths problem (Many-Many): Find a
shortest path from u to v for every pair of vertices u and v.
We talk about directed, weighted graphs

Shortest-Path Variants (Cont’d)
• For un-weighted graphs, the shortest path problem is mapped to BFS
– Since all weights are the same, we search for the smallest number of edges
s
2
5
4
7
8
3 6 9
0
1
1
1
2
2
3
3
3
BFS creates a tree called BFS-Tree

• Single-source single-destination (1-1): Find the shortest
path from source s to destination v.
• Single-source all-destination(1-Many): Find the shortest
path from s to each vertex v.
• Single-destination shortest-paths (Many-1): Find a shortest
path to a given destination vertex t from each vertex v.
• All-pairs shortest-paths problem (Many-Many): Find a
shortest path from u to v for every pair of vertices u and v.
No need to consider different solution or algorithm for each variant
(we reduce it into two types)

Single-Source Single-Destination (1-1)
- No good solution that beats 1-M variant
- Thus, this problem is mapped to the 1-M
variant
Single-Source All-Destination (1-M)
- Need to be solved (several algorithms)
- We will study this one
All-Sources Single-Destination (M-1)
- Reverse all edges in the graph
- Thus, it is mapped to the (1-M) variant
All-Sources All-Destinations (M-M)
- Need to be solved (several algorithms)
- We will study it (if time permits)

Introduction
Generalization of BFS to handle weighted graphs
• Direct Graph G = ( V, E ), edge weight fn ; w : E → R
• In BFS w(e)=1 for all e  E
Weight of path p = v1  v2  …  vk is
1
1
1
( ) ( , )
k
i i
i
w p w v v



 

Shortest Path
Shortest Path = Path of minimum weight
δ(u,v)= min{ω(p) : u v}; if there is a path from u to v,
 otherwise.
p

1- Optimal Substructure Property
Theorem: Subpaths of shortest paths are also shortest paths
• Let δ(1,k) = <v1, ..i, .. j.., .. ,vk > be a shortest path from v1 to vk
• Let δ(i,j) = <vi, ... ,vj > be subpath of δ(1,k) from vi to vj
for any i, j
• Then δ(I,j) is a shortest path from vi to vj

Proof: By cut and paste
• If some subpath were not a shortest path
• We could substitute a shorter subpath to create a shorter
total path
• Hence, the original path would not be shortest path
v2
v3 v4
v5 v6 v7
1- Optimal Substructure Property
v1
v0

Definition:
• δ(u,v) = weight of the shortest path(s) from u to v
• Negative-weight cycle: The problem is undefined
– can always get a shorter path by going around the cycle again
• Positive-weight cycle : can be taken out and reduces the cost
s v
cycle
< 0
2- No Cycles in Shortest Path

3- Negative-weight edges
• No problem, as long as no negative-weight cycles are
reachable from the source (allowed)

4- Triangle Inequality
Lemma 1: for a given vertex s in V and for every edge (u,v) in E,
• δ(s,v) ≤ δ(s,u) + w(u,v)
Proof: shortest path s v is no longer than any other path.
• in particular the path that takes the shortest path s v and
then takes cycle (u,v)
s
u v

Algorithms to Cover
• Dijkstra’s Algorithm
• Shortest Path is DAGs

Initialization
• Maintain d[v] for each v in V
• d[v] is called shortest-path weight estimate
and it is upper bound on δ(s,v)
INIT(G, s)
for each v  V do
d[v] ← ∞
π[v] ← NIL
d[s] ← 0
Parent node
Upper bound

Relaxation
RELAX(u, v)
if d[v] > d[u]+w(u,v) then
d[v] ← d[u]+w(u,v)
π[v] ← u
5
u v
v
u
2
2
9
5 7
Change d[v]
5
u v
v
u
2
2
6
5 6
When you find an edge (u,v) then
check this condition and relax d[v] if
possible
No chnage

• Non-negative edge weight
• Like BFS: If all edge weights are equal, then use BFS,
otherwise use this algorithm
• Use Q = min-priority queue keyed on d[v] values
Dijkstra’s Algorithm For Shortest Paths

DIJKSTRA(G, s)
INIT(G, s)
S←Ø > set of discovered nodes
Q←V[G]
while Q ≠Ø do
u←EXTRACT-MIN(Q)
S←S U {u}
for each v in Adj[u] do
RELAX(u, v) > May cause
> DECREASE-KEY(Q, v, d[v])
Dijkstra’s Algorithm For Shortest Paths

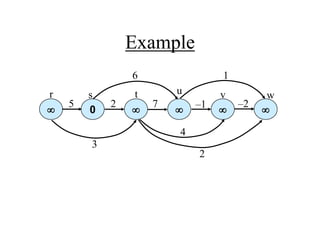
Example: Initialization Step
3
¥ ¥
¥ ¥
0
s
u v
y
x
10
5
1
2 9
4 6
7
2
DIJKSTRA(G, s)
INIT(G, s)
Q←V[G]
while Q ≠Ø do
u←EXTRACT-MIN(Q)
S←S U {u}

Example
3
 
 
0
s
u v
y
x
10
5
1
2 9
4 6
7
2

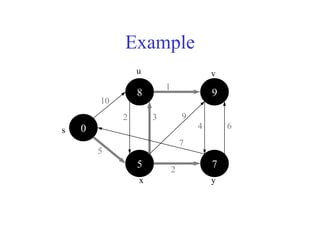
Example
2
10 
5 
0
s
u v
y
x
10
5
1
3
9
4 6
7
2
DIJKSTRA(G, s)
INIT(G, s)
Q←V[G]
while Q ≠Ø do
u←EXTRACT-MIN(Q)
S←S U {u}

Example
2
8 14
5 7
0
s
y
x
10
5
1
3 9
4 6
7
2
u v
DIJKSTRA(G, s)
INIT(G, s)
Q←V[G]
while Q ≠Ø do
u←EXTRACT-MIN(Q)
S←S U {u}

Example
10
8 13
5 7
0
s
u v
y
x
5
1
2 3 9
4 6
7
2
DIJKSTRA(G, s)
INIT(G, s)
Q←V[G]
while Q ≠Ø do
u←EXTRACT-MIN(Q)
S←S U {u}

Example
8
u v
9
5 7
0
y
x
10
5
1
2 3 9
4 6
7
2
s
DIJKSTRA(G, s)
INIT(G, s)
Q←V[G]
while Q ≠Ø do
u←EXTRACT-MIN(Q)
S←S U {u}

Example
u
5
8 9
5 7
0
v
y
x
10
1
2 3 9
4 6
7
2
s

Dijkstra’s Algorithm Analysis
DIJKSTRA(G, s)
INIT(G, s)
Q←V[G]
while Q ≠Ø do
u←EXTRACT-MIN(Q)
S←S U {u}
O(V)
O(V Log V)
Total in the loop: O(V Log V)
Total in the loop: O(E Log V)
Time Complexity: O (E Log V)

Key Property in DAGs
• If there are no cycles  it is called a DAG
• In DAGs, nodes can be sorted in a linear order such that all
edges are forward edges
– Topological sort

Single-Source Shortest Paths in DAGs
• Shortest paths are always well-defined in dags
 no cycles => no negative-weight cycles even if
there are negative-weight edges
• Idea: If we were lucky
 To process vertices on each shortest path from left
to right, we would be done in 1 pass

Single-Source Shortest Paths in DAGs
DAG-SHORTEST PATHS(G, s)
TOPOLOGICALLY-SORT the vertices of G
INIT(G, s)
for each vertex u taken in topologically sorted order do
RELAX(u, v)

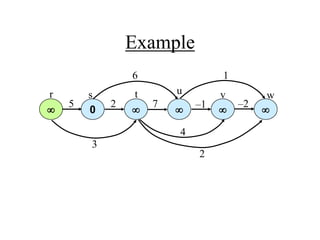
Example
 0    
r s t u v w
5 2 7 –1 –2
6 1
3
2
4

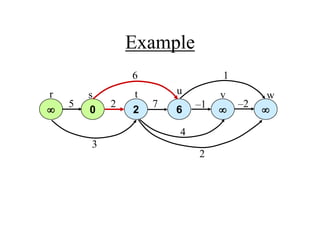
Example
 0 2 6  
r s t u v w
5 2 7 –1 –2
6 1
3
2
4

Example
 0 2 6 6 4
r s t u v w
5 2 7 –1 –2
6 1
3
2
4

Example
 0 2 6 5 4
r s t u v w
5 2 7 –1 –2
6 1
3
2
4

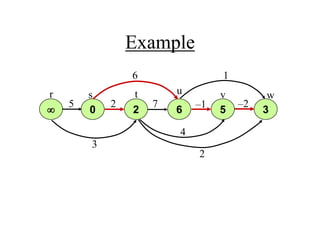
Example
 0 2 6 5 3
r s t u v w
5 2 7 –1 –2
6 1
3
2
4

Single-Source Shortest Paths in
DAGs: Analysis
DAG-SHORTEST PATHS(G, s)
TOPOLOGICALLY-SORT the vertices of G
INIT(G, s)
for each vertex u taken in topologically sorted order do
RELAX(u, v)
O(V+E)
O(V)
Total O(E)
Time Complexity: O (V + E)

Shortest path

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Similar to Shortest path

Similar to Shortest path (20)

More from Ruchika Sinha

More from Ruchika Sinha (20)

Recently uploaded

Recently uploaded (20)

Shortest path